基于图谱特征的塔式起重机塔身损伤判断方法研究

张会敏，宋世军

（1.泰山学院机械与建筑工程学院，山东泰安271000；2.山东建筑大学机电工程学院，山东济南250101）

塔式起重机作为一种大型高危特种设备，因其安装拆卸方便、工作空间大、工作效率高、起升高度高等诸多优点，在建筑行业得到广泛的运用。但是由于结构疲劳损伤、塔身主肢断裂、塔身高强螺栓松动等塔身损伤造成的事故数不胜数［1-3］。为了保证塔机的安全运行，对塔身损伤检测的实效性、准确性和可靠性提出了新的要求。目前损伤检测研究对象大多是简单结构或部件，对于塔机之类的大型复杂结构、损伤检测的研究相对较少。因此，迫切需要找到一种方便快捷的方法，实现对塔身状态的快速检测，及时排除隐患，保证塔机的安全运行。

本文利用塔机ANSYS模型和ADAMS模型获取塔身顶端轨迹特征图谱［4-5］，借助Matlab的Cftool功能，基于时间序列对归一化后的轨迹进行3次正弦和函数拟合。通过不同状态下拟合参数的综合比较，找到了区分塔身不同状态的敏感特征量，构造出塔身损伤的判断方法以及损伤判据，进而实现塔身状态的快速检测。

1 动态仿真模型建立

根据QTZ40塔机尺寸结构参数，建立塔机有限元模型。根据不同载荷状态下塔机ANSYS模型各个钢结构单元的变形量，确定ADAMS环境中连接钢结构单元之间弹簧刚度值，使Adams中模型各部分的变形量与ANSYS模型变形量一致。在ADAMS软件中建立塔机动态仿真模型，并确定轨迹信号特征点［2］，此特征点在ADAMS模型中取为marker893点。塔机动态仿真模型及检测点如图1和图2所示。

图1 塔机动态仿真模型Fig.1 Dynamic simulation model of tower

图2 检测点示意图Fig.2 Schematic diagram of test points

2 塔身顶端轨迹图谱数据获取

调整ADAMS模型中塔身第1层连接螺栓的刚度值，获取塔身完好状态、单主肢（1号主肢）损伤、同一层相邻两主肢（1号、4号主肢）同步损伤、同一层对角两主肢（1号、3号主肢）同步不同损伤状态时的塔身顶端轨迹。损伤位置如图3所示。

图3 塔身主肢损伤位置图Fig.3 Damage location of tower main limb

由于ADAMS环境中仿真得到的是监测点在以地面为参照量的静坐标系数据，要得到监测点在以塔身回转台为参照量的动坐标系下的数据，需要将静坐标系的数据转化到动坐标系下，转化公式为

式中：X、Y为静坐标系下的数据；X'、Y'为动坐标下的数据。

3 塔身顶端轨迹图谱数学建模

3.1 轨迹归一化处理

考虑转换到动坐标系的轨迹形状与损伤程度有关，图形的形状、分布区域都不相同，因此，可用归一化公式将获得的数据沿x、y两个方向进行归一化处理，将数据缩放到特定区域，归一化公式为

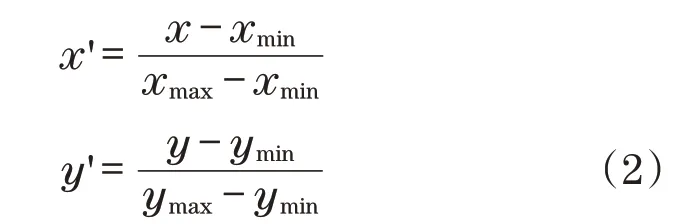
式中：x、y为塔身转到不同角度时x、y两个方向的坐标；x'、y'为x、y归一化处理后的坐标；xmax、ymax分别为x、y两个方向坐标的最大值；xmin、ymin分别为x、y两个方向坐标的最小值。

塔身不同损伤状态下的顶端轨迹数据经过归一化后的图形如图4~图7所示。

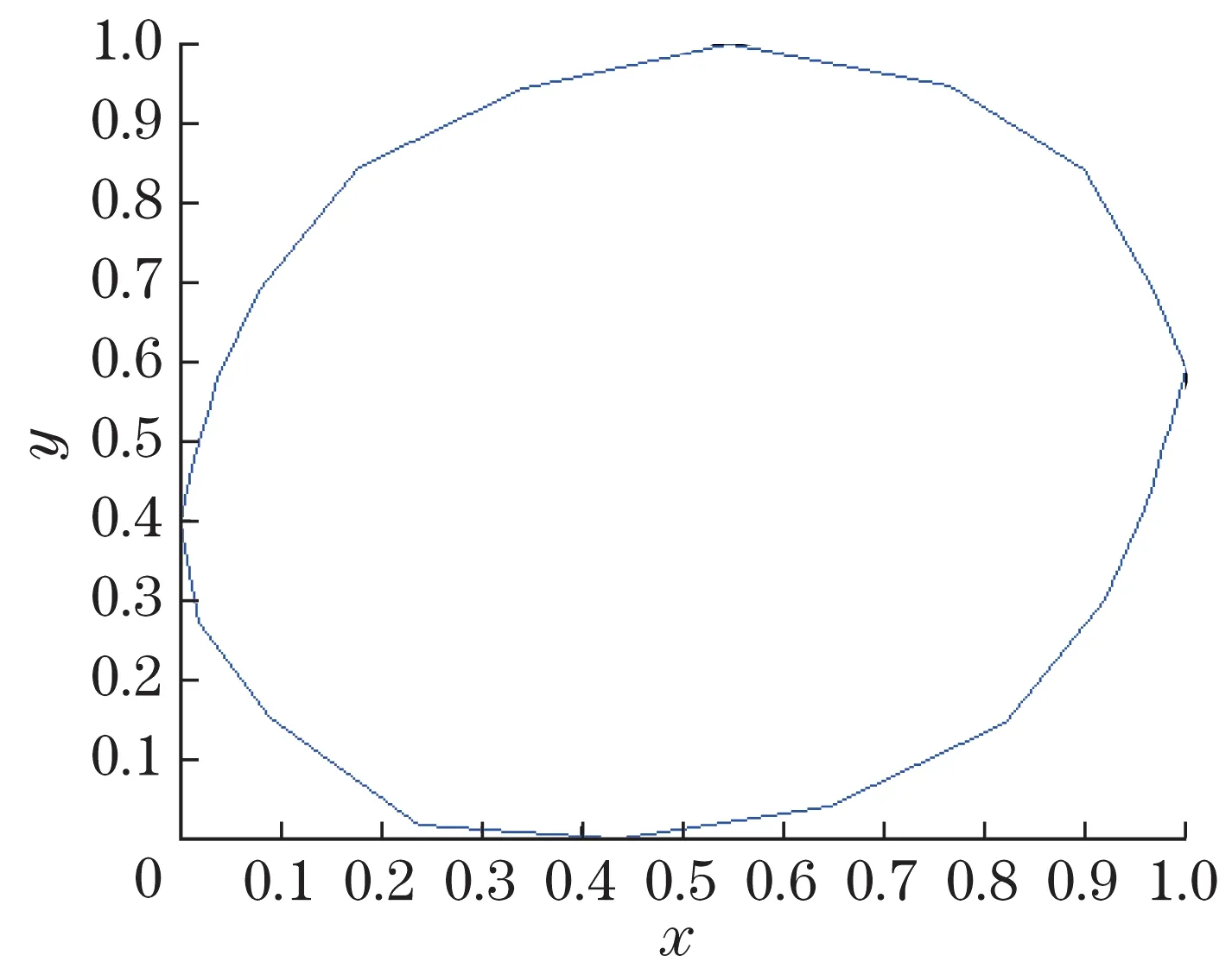
图4 完好状态下归一化轨迹Fig.4 Normalized trajectory in good condition

3.2 塔身顶端轨迹特征建模

通过图4~图7可知，塔身单主肢不同损伤和对角主肢同步损伤时的归一化模型均近似重合，相邻主肢损伤小于1/2时归一化轨迹近似重合，损伤大于1/2时轨迹内敛部分不重合。因此，可以构造一个数学模型，通过调整模型参数，实现对各归一化模型的数学描述，并根据模型参数的不同，达到损伤类型判断的目的。

图7 对角主肢损伤归一化轨迹Fig.7 Nor malized tr ajector y of diagonal main limb in damage condition

将模型轨迹基于时间序列沿x、y两个方向分别展开，并利用Matlab的Cftool拟合功能进行不同类型拟合，通过比较分析发现，当选用3次正弦和函数拟合时，对于各两个方向的轨迹拟合效果均已经比较理想，考虑应尽可能减少参数个数，选择用3次正弦和函数拟合归一化轨迹。单主肢损伤1/2时，单向拟合效果图与整体拟合效果，如图8和图9所示。

图5 单主肢损伤归一化轨迹Fig.5 Normalized trajectory of single main limb in damage condition

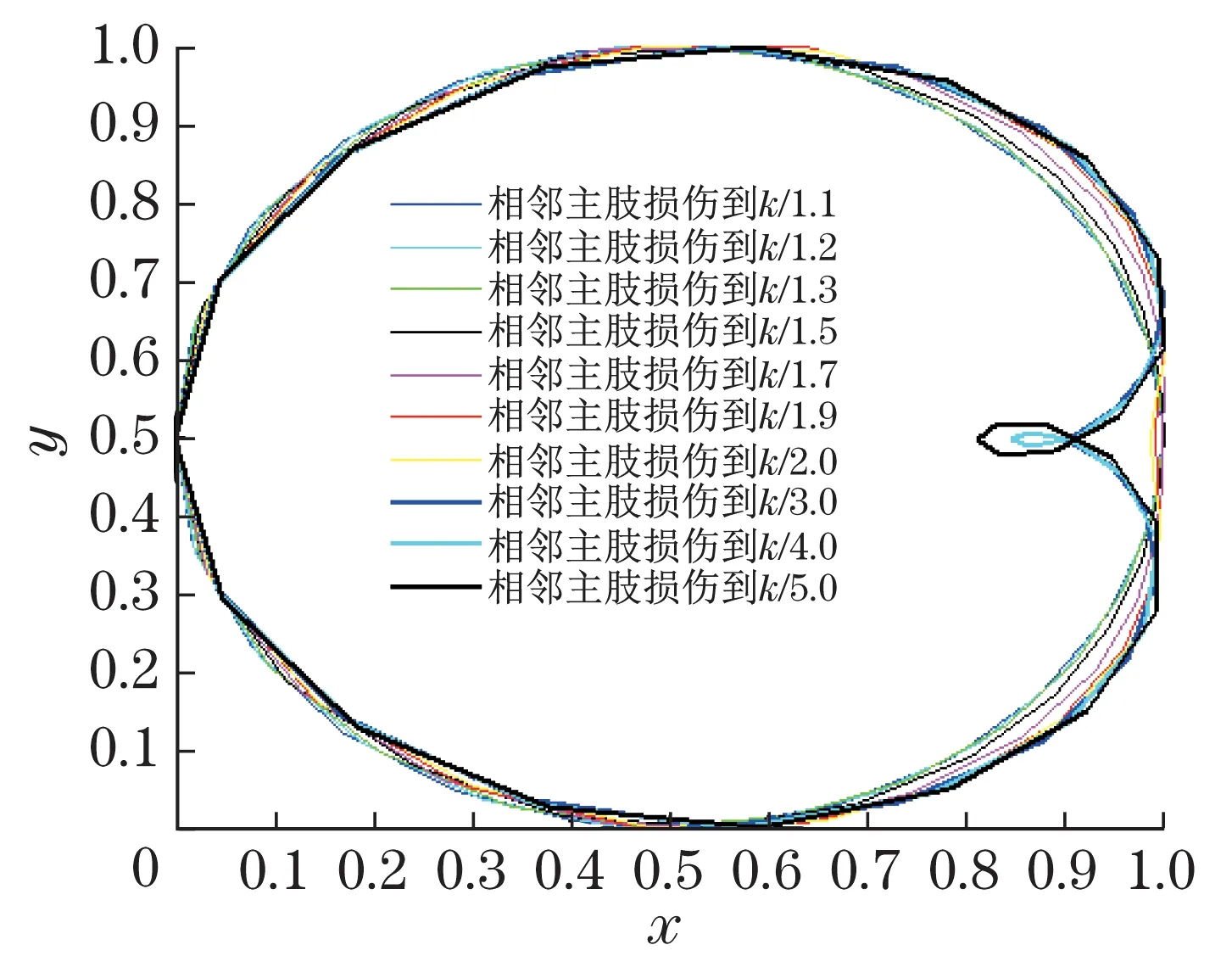
图6 相邻主肢损伤归一化轨迹Fig.6 Normalized trajectory of adjacent main limb in damage condition

图8 x、y方向拟合效果图Fig.8 Fitting result diagram in the x，y direction

图9 归一化模型拟合效果图Fig.9 Fitting result diagram of normalized model

因此，将x方向的轨迹多项式记为j，y方向的轨迹多项式记为k，则

4 损伤判据的确定

4.1 损伤类型判断

为消除拟合过程中初始搜索区域对拟合结果的影响，准确寻找数学模型中区分塔身不同状态的敏感特征量，利用Matlab的Cftool拟合功能将塔身轨迹归一化模型数据，按式（5）各进行12次拟合求解，并将每次拟合的3组参数作为三角形的3个顶点，构造空间直角坐标系o-abc，得到参数空间分布如图10和图11所示。

图11 塔身不同状态下y方向拟合参数的空间分布图Fig.11 Spatial distribution of the fitting parameters in the y direction of the tower in different states

通过图10可知，在x、y方向中，ab平面内各三角形中距离a轴最近的点均出现聚集，且塔身状态相同时，b的该点簇关于直线a=0对称，塔身状态不同时，点簇到直线a=0的距离随损伤状态的不同而发生变化。结合塔身顶端轨迹模型形式的可知，该点的坐标值是模型参数中的周期分量，记录主要的图谱信息，且参数相对固定，不会受搜索域的影响，其他拟合参数为随机分量，对图谱信息的承载量相对较少，因此，可以用任一方向的周期分量参数为基础，构造损伤判据。现以x方向周期分量为基础，寻找损伤判据。

图10 塔身不同状态下x方向拟合参数的空间分布图Fig.10 Spatial distribution of the fitting parameters in the x direction of the tower in different states

用均值法求得方向|a|、b均值，并绘制不同损伤状态下参数|a|和参数b的折线图，如图12和图13所示。k为塔身主肢标准刚度值。

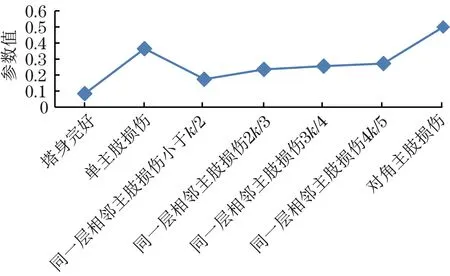
图12 不同损伤状态下参数|a|的取值Fig.12 Par ameter value of|a|in different damage states

图13 不同损伤状态下参数b的取值Fig.13 Parameter value of b in different damage states

从图12和图13可知，|a|、b的取值与塔身状态有关：①塔身完好状态时，周期分量中的参数b≈7.8，塔身损伤时，b≈5.2；②塔身完好状态时，|a|≈0.08，单主肢损伤时|a|∈（0.35，0.4），同一层相邻主肢损伤时|a|∈（0.15，0.3），同一层对角主肢损伤时|a|≈0.5。因此，通过b的取值范围，可以判断是否出现损伤，通过|a|的取值范围，可以定性判断损伤类型。

4.2 损伤程度判断

文献［5］损伤的判断是通过损伤图谱面积的大小以及远离中心点的位置判断损伤的程度，该方法在已知损伤状态的情况下，能够较好地判断出损伤程度，但是在塔身情况未知的情况下，判断损伤状态及损伤程度，结果不是很理想。因此，在采用以上方法判断出损伤类型的情况下，可以用图谱外接矩形面积的方法判断损伤程度的大小，不同损伤状态下，塔身顶端轨迹外接矩形面积如图14示。

图14 不同损伤状态下塔身顶端轨迹外接矩形的面积图Fig.14 External rectangular area of the tr ajector y at the top of the tower in different damage states

由图14可知，无论何种损伤状态下，塔身顶端轨迹外接矩形面积都随损伤程度的增加而增大。在已知损伤状态的前提下，通过外接矩形面积的大小，能够较好的判断损伤程度的大小。

5 结语

本研究建立了塔身顶端轨迹图谱的数学模型，借助Matlab对模型参数进行拟合比较，并结合塔身图谱外接矩形面积的大小，找到了塔身损伤状态的判断方法。该方法能够通过模型参数的不同，判断塔身是否发生损伤和损伤的类型，并通过外接矩形面积的大小判断损伤程度，为塔身状态的全面、快速检测提供了一种新方法。