二次模态分解组合DBiLSTM-MLR 的综合能源系统负荷预测

陈锦鹏，胡志坚，陈纬楠，高明鑫，杜一星，林铭蓉

（武汉大学电气与自动化学院，湖北省武汉市430072）

0 引言

为实现能量精确管理，综合能源系统（IES）应运而生［1］。多种能源在IES 中相互转换，使得多元负荷存在一定的耦合关系［2］，对负荷预测也提出了更高要求。

传统方法与机器学习［3-6］预测速度快，但忽略了样本时序关系［7］。近年来，深度学习有了广泛应用，典型代表就是长短期记忆（LSTM）神经网络［8-9］。为简化模型，文献［10］通过主成分分析实现数据降维后运用深度双向长短期记忆（DBiLSTM）神经网络预测，但主成分分析只能提取数据的线性关系，尽管深度学习能挖掘序列时序特征，但在面对非连续序列时预测精度也有限。

为发挥各种模型优势，文献［11］运用受限玻尔兹曼机与递归神经网络的组合模型；文献［12］运用LSTM 神经网络和轻梯度提升机进行预测后采用最优加权组合法对结果进行重构；文献［13-14］采用门控循环单元结合统计学方法，也取得了不错的效果。

为进一步提升预测精度，文献［15］采用变分模态分解（VMD）将风速序列分解成多个本征模态分量（IMF）后运用LSTM 神经网络预测，但VMD 存在所有分量重构后与原序列不一致的缺陷；文献［16］运用经验模态分解，虽然各分量重构后与原序列一致，但经验模态分解存在模态混叠现象，且分解后的高频分量为强非平稳分量，预测该分量将产生较大误差；文献[17]为降低小波包分解产生的强非平稳分量对预测的影响，采用集合经验模态分解对该分量再次分解，但集合经验模态分解引入了噪声，且2 次分解产生的分量众多，均由神经网络预测将耗费很高的时间成本；对此，文献［18］将集合经验模态分解产生的非平稳分量由门控循环单元预测，平稳分量由多元线性回归（MLR）预测，节省了很多时间成本，但同样存在引入噪声及分解后高频分量难以准确预测的问题。

针对IES 多元负荷预测，文献［1-2］通过构建多任务学习模型进行多元负荷预测；文献［19］结合气象预测进一步提高多元负荷预测精度；文献［20］采用卷积神经网络提取特征后由LSTM 神经网络进行预测。

目前针对IES 多元负荷预测的研究较少［20］，且对于用户级IES 来说，多元负荷随机、波动性相对更强。为此，本文提出一种基于核主成分分析（KPCA）、二次模态分解（QMD）、DBiLSTM 神经网络和MLR 的多元负荷预测模型。首先，运用自适应噪声的完全集合经验模态分解（CEEMDAN）对电、冷、热负荷进行分解，考虑到高频IMF 为强非平稳序列，因此运用VMD 再次分解。然后，运用KPCA 将特征集映射到高维空间，保留数据非线性关系后提取主成分实现数据降维；综合深度学习对非平稳序列学习能力更强以及回归分析法能保证预测精度下对平稳序列快速预测的特点，将分解得到的非平稳、平稳序列分别用DBiLSTM 神经网络、MLR 进行预测。算例结果表明，本文所提模型相比其他模型具有更高的预测精度。

1 QMD 原理

1.1 CEEMDAN 原理

CEEMDAN 是一种后验的、自适应的时频分解法，适合将非平稳序列平稳化。不同于小波分解须人为设置小波基［21］，CEEMDAN 能够自适应地将序列分解为有限个不同时间尺度的IMF，记为CIMF。通过在原始信号中加入符号相反的白噪声，解决了经验模态分解存在的模态混叠现象和集合经验模态分解引入白噪声的问题。

将多元负荷序列进行模态分解，可以降低预测难度。以原始电负荷为例进行分析，CEEMDAN 分解的基本步骤如下。

步骤1:向原始电负荷序列加入M对符号相反的白噪声，即

步骤2:运用经验模态分解分别对2 个电负荷新序列进行模态分解，得到2 组CIMF 分量。

步骤3:重复M次步骤2，得到2 组集成的CIMF分量，即

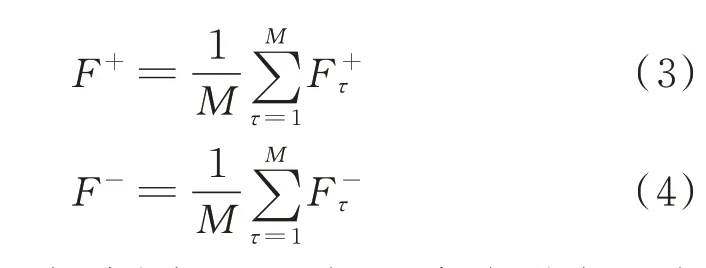
式中:F+和F-分别为加入M次正、负白噪声后分解获得的CIMF 分量组平均值；F+τ和Fτ分别为第τ次加入正、负白噪声后分解获得的分量组。

步骤4:取F+和F-的平均值即为最终电负荷序列分解结果。

经验模态分解的基本公式为:

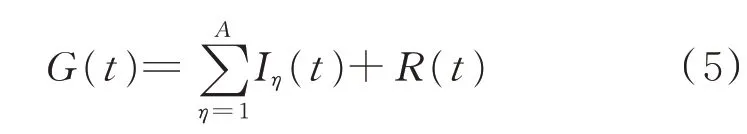
式中:Iη(t)为第η个IMF 分量；A为分解后CIMF数；R(t)为残余分量。

1.2 VMD 原理

CEEMDAN 分解产生的高频分量为强非平稳分量，直接预测这部分分量往往误差较大。

VMD 是一种在2014 年提出的自适应分解方法，适合处理非平稳序列。CEEMDAN 采用递归求解方式，其分解产生的所有CIMF 重构后与原始序列一致；VMD 则采用完全非递归方式求解，将原始序列分解为多个不同中心频率的有限带宽IMF 分量，记为VIMF，每个分量都较平稳，但分解产生的所有VIMF 重构后与原始序列不一致，分解个数越多，重构后与原始序列越相近。QMD 对提高负荷预测精度影响的详细分析见附录A 图A1。对1.1 节中原始电负荷序列经CEEMDAN 分解产生的强非平稳分量运用VMD 再次分解的步骤如下。

1)构造约束变分最优问题

2）利用二次惩罚因子α和Lagrange 乘子λ(t)，将式（6）转化为无约束问题:

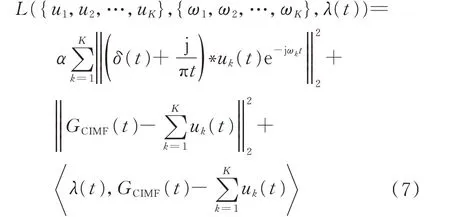
式中:· 表示求内积。

3）利用交替方向乘子算法寻优，不断更新uk、ωk，获得指定分解个数的VIMF 分量，详细求解过程可参考文献［22］。

2 KPCA 原理

通常模型的输入会考虑天气等特征变量。这些特征集的引入导致模型的输入维度大大增加，使得模型变得更加复杂，同时也增加了模型的训练时间。

不同于主成分分析只能提取数据的线性主成分，KPCA 通过核函数将一组多维非线性数据映射到高维空间，使其在高维空间中变得线性可分，再利用主成分分析提取主成分，能够在保留多维数据之间非线性关系的同时降低数据维度。其基本过程如下。

1）设 有 一 组N维 数 据U=[d1，d2，…，dN]，此N维数据在文中即为影响IES 多元负荷的天气、日历规则特征集。天气因素即为与多元负荷相对应的温度、湿度等气象因素，日历规则即为与多元负荷相对应的时间，如第几月、第几日、星期几、第几小时等。利用满足Mercer 条件的非线性核函数Φ对U进行高维映射后得到Q:

3）结合Mercer 定理可将式（9）转化为式（11）求取特征值问题:

式中:H为N×N核矩阵；pH=[pH1，pH2，…，pHN]为对应H矩阵的特征向量；λH=[λH1，λH2，…，λHN]，且λH1＞λH2＞…＞λHN为对应pH的特征值。

4）根据所需的累积贡献率ς，选取前χ个特征值之和rχ使得rχ≥ς，选取前χ个特征值对应的特征向量构成一个χ维特征空间，使样本在χ维空间内进行投影，即为天气、日历规则特征集χ个核主成分。rχ的计算式为:

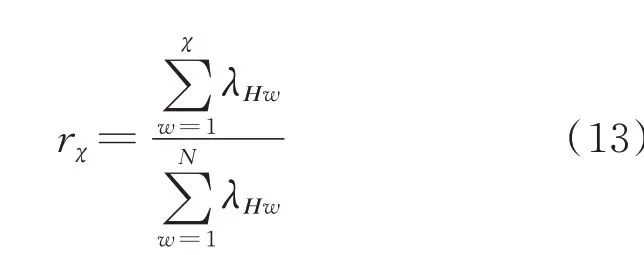
3 MLR 模型

MLR 通过构造一个含多变量的线性方程，可对平稳序列准确拟合，且速度极快。MLR 进行多元负荷预测的回归模型为:

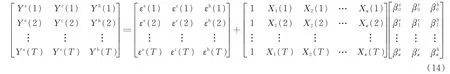
式中:Ye、Yc、Yh分别为电、冷、热负荷经QMD 分解后的平稳分量值；εe、εc、εh分别为电、冷、热负荷的随机误差值；T为参与回归的样本数量；Xκ为影响多元负荷因素，在本文中即为历史电、冷、热负荷值及天气、日历规则经KPCA 提取的主成分；κ为影响多元负荷因素数量；βeκ、βcκ、βhκ为分别为电、冷、热负荷回归系数。

将上式简写为:

式中:Y为多元负荷矩阵；ε为随机误差矩阵；X为影响因素矩阵；β为回归系数矩阵。

采用最小二乘估计求得回归系数矩阵β的估计量β^，得到回归预测模型，即

关于MLR 在预测平稳序列上的优势分析见附录A 图A2 和表A1。虽然MLR 在预测平稳序列时表现优异，然而在面对非平稳序列时MLR 往往表现不佳，而诸如LSTM 神经网络这类预测模型能够取得不错的效果。

4 DBiLSTM 神经网络模型

由于循环神经网络存在梯度消失等问题，因此LSTM 神经网络对此进行了改进。LSTM 单元由输入门、遗忘门、输出门组成，通过对门的控制排除干扰数据，可有效提高记忆能力，其结构如附录A图A3 所示，各门计算公式如下。

1）遗忘门

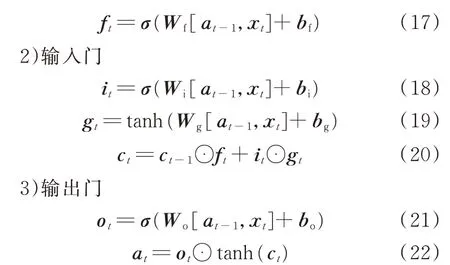
式中:ft、it、gt、ct、ot、at分别为t时刻各门的特征变量；Wf、Wi、Wg、Wo分别为各门的权重矩阵；bf、bi、bg、bo分别为各门的偏置项；xt为t时刻输入变量；at-1和at分别为t-1 和t时刻输出变量；σ和tanh 为激活函数；⊙为哈达玛积。

LSTM 神经网络训练时，通过单向时序输入对隐含层状态进行传递更新。然而多元负荷当前时刻与前后时段都具有相关性，传统训练方式忽略了历史数据的全局信息，同时若样本的时间长度较长，也会使LSTM 神经网络遗忘掉早期学习到的内容。

双向长短期记忆神经网络可解决该问题，其本质上由正反2 个独立的LSTM 网络组成，每一时步的输出均由正反两向LSTM 共同组成，可对历史数据进行正反两向训练，从历史数据中学到更多有效信息，其基本结构如图1 所示。

图1 双向长短期记忆神经网络结构Fig.1 Structure of bidirectional long short-term memory neural network

通过构建多层双向长短期记忆神经网络隐含层，进而构成DBiLSTM 神经网络，各隐含层将正反两向LSTM 神经网络输出进行结合作为该隐含层的最终输出，表达式为:

将电、冷、热负荷经QMD 分解后的非平稳分量和天气、日历规则经KPCA 提取的主成分组成输入集，运用DBiLSTM 神经网络进行训练，选取均方误差EMSE计算模型损失值，结合Adam 优化算法进行模型的权重更新。EMSE表达式为:

5 多元负荷预测模型

5.1 多元负荷预测模型总体框架

本文结合KPCA、QMD、DBiLSTM 神经网络及MLR（KQDM）所建立的模型总体框架如图2 所示。分别对电、冷、热负荷运用CEEMDAN 进行第1 次分解后，将一次分解产生的强非平稳CIMF 分量再次运用VMD 进行第2 次分解，得到最终的本征模态分量集；对天气、日历规则特征集运用KPCA 提取主成分实现降维；考虑到DBiLSTM 神经网络对非平稳分量的拟合能力更强，结合MLR 对平稳分量所表现出的优异性能，因此将电、冷、热负荷分解后的非平稳分量与降维后的主成分集作为输入运用DBiLSTM 神经网络进行预测，将电、冷、热负荷分解后的平稳分量与降维后的主成分集作为输入运用MLR 进行预测，最后将所有预测结果进行重构，得到最终预测结果。

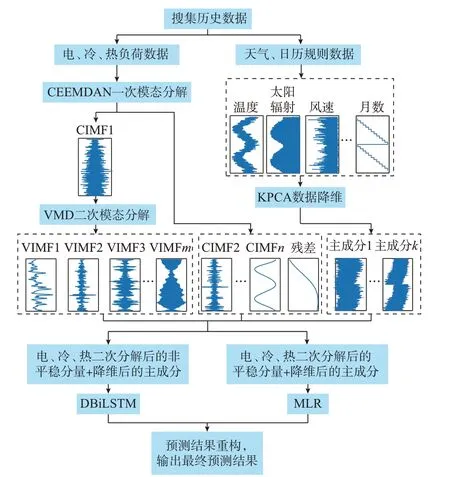
图2 KQDM 模型总体框架Fig.2 Overall framework of KQDM model

5.2 评价指标

以平均绝对百分比误差EMAPE和均方根误差ERMSE对预测结果进行评价，表达式如下。

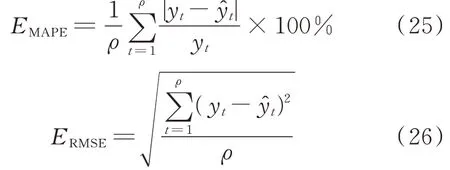
式中:ρ为参与计算的样本个数；yt和y^t分别为t时刻的真实值和预测值。

6 算例分析

本文以美国亚利桑那州立大学［23］坦佩校区的IES 数据作为实验数据，该校区属于用户级IES。天气数据考虑温度、风速、湿度、太阳垂直辐射、太阳水平辐射、露点和大气压，在美国国家可再生能源实验室官网［24］内的国家太阳辐射数据库中，选择与坦佩校区最近的气象站点进行下载。日历规则考虑月数、周数、天数、小时数和节假日，天气、日历规则数据共12 维。电、冷、热负荷及天气数据的波形见附录A 图A4。

结合附录A 图A4 可知，电、冷负荷曲线走向大致相同，均表现为“夏高冬低”的特征，而热负荷则相反，呈现“夏低冬高”的特征，表明电、冷负荷与热负荷呈现很强的季节互补特性。为了直观刻画电、冷、热负荷之间的耦合关系，附录A 表A2 给出运用Spearman 秩相关系数进行电、冷、热负荷之间的相关性量度，可见3 种负荷之间相关性均大于0.8，属于强相关关系，验证了运用多元负荷预测方法进行预测的优越性。

选 择2018 年1 月1 日 至2019 年12 月31 日，按8∶1∶1 划分训练集、验证集、测试集，以1 h 为步长进行预测。

实验硬件平台为Intel Core i7-8700 CPU，采用NVDIA GTX 1050Ti GPU 进行加速；软件平台采用Python 语言，在Tensorflow 框架下实现。

6.1 多元负荷分解与特征集降维

6.1.1 基于QMD 实现电、冷、热负荷模态分解

利用QMD 对初始负荷数据进行模态分解。分别对3 种负荷进行CEEMDAN 模态分解，得到的电负荷分解结果如图3 所示，冷、热负荷分解结果见附录A 图A5 和图A6。

图3 电负荷CEEMDAN 模态分解结果Fig.3 CEEMDAN modal decomposition results of electric load

采用近似熵［25］对分解产生的模态分量进行平稳性量度。电、冷、热负荷经过CEEMDAN 分解后产生的CIMF1 分量均为强非平稳分量，运用VMD分别对其进行二次分解。考虑到分解产生的VIMF分量越多，重构后与分解前的CIMF1 越相近，同时由于VMD 二次分解产生的VIMF 分量均为平稳分量，可以由MLR 进行预测，所需耗费的时间很短，因此将3 种负荷的CIMF1 分量均由VMD 再次分解为80 个VIMF 分量，电、冷、热负荷二次分解结果见附录A 图A7 至图A9，QMD 分解后最终各分量近似熵值见附录A 图A10。

6.1.2 基于KPCA 实现特征集数据降维

本文采用的特征集数据共12 维，若与多元负荷数据共同输入模型就多达15 维，增加了模型的复杂度。因此利用KPCA 对特征集进行数据降维。表1为经KPCA 提取的前6 个主成分，可以看出，前6 个主成分的累积方差贡献率已高达89.02%，已经包含原来12 维特征集的大部分信息，因此选择前6 个主成分代替原来12 维特征集，提取后的前6 个主成分波形见附录A 图A11。

表1 KPCA 提取的主成分结果Table 1 Extraction results of principal components by KPCA

为体现KPCA 提取的主成分与原始特征集之间的关系，给出KPCA 提取结果，见附录A 表A3。表中数值越大，表示该主成分中包含该影响因素的比重越大。可知，第1 主成分主要包含温度、湿度、太阳垂直辐射、太阳水平辐射影响因素；第2 主成分主要包含月数、周数影响因素；第3 主成分主要包含小时数影响因素；第4 主成分主要包含天数、小时数影响因素；第5 主成分主要包含湿度、月数、周数、天数、小时数影响因素；第6 主成分主要包含温度、露点影响因素。

可以看出，第1 和第6 主成分主要为天气影响因素，第2 到第5 主成分主要为日历规则影响因素，前6 个主成分已基本涵盖多元负荷预测所需的天气、日历规则特征集信息。

6.2 模型参数设置

模型的输入为预测时刻前6 h 的电、冷、热负荷数据及特征集降维后的6 个主成分共9 维，输出为待预测时刻电、冷、热负荷。

DBiLSTM 神经网络层数2 层，隐含神经元分别为50 个和100 个；学习率为0.01；优化算法为Adam；添加Dropout 为0.3 以防止过拟合；迭代次数为200 次。

6.3 结果分析

6.3.1 模态分解前后对比分析

为分析模态分解对多元负荷预测精度的影响，随 机 选 取2019 年11 月17 日 至2019 年11 月23 日 预测结果进行对比，以不进行模态分解、进行CEEMDAN 一次模态分解和进行CEEMDAN 及VMD 二次模态分解进行实验对比，结果如图4 和表2 所示。其中，电、热、冷之间单位的关系为:1 MW=3.4 mmBTU/h=284 Ton。

图4 模态分解前后电、冷、热负荷预测结果Fig.4 Prediction results of electric, cooling and thermal load before and after modal decomposition

表2 模态分解前后预测精度结果Table 2 Prediction accuracy results before and after modal decomposition

可以看出，不进行模态分解的预测精度最差，电、冷、热负荷的预测误差EMAPE分别为2.32%、4.23%、4.12%；进行CEEMDAN 一次模态分解时的预测精度次优，EMAPE分别为1.38%、2.17%、2.11%，精度提升了近1 倍；而进行CEEMDAN 及VMD 二次模态分解时的预测精度最好，EMAPE分别为0.47%、0.95%、0.92%，精度提升了4～5 倍。由于用户级IES 多元负荷随机、波动性相对较强，直接预测将产生较大的误差。虽然进行一次模态分解能够在一定程度上提高预测精度，但分解产生的高频强非平稳分量无法进行准确预测，而这部分分量正是包含原始负荷曲线里的随机波动分量，因此一次模态分解只是提升了对负荷大致趋势的预测，对于负荷的小范围波动则无法准确预测；而进行二次模态分解后，VMD 将CEEMDAN 分解产生的强非平稳分量再次分解为多个平稳分量，大大提升了这部分强非平稳分量的预测精度，使最终的预测精度有了较大的提升。

6.3.2 KPCA 提取主成分前后对比分析

考虑KPCA 前后的预测结果如表3 所示。可知，运用KPCA 提取主成分，使模型的输入维度大为降低，模型结构参数有了一定的减少，因此花费的时间成本更低，相较不运用KPCA 节省了16.03 s。并且，考虑KPCA 提取主成分后进行预测的精度更高，这是因为提取的所有主成分中，风速、节假日等影响因素的比重均很小，由于多元负荷主要受温/湿度、太阳辐射、天数、小时数等影响，减小风速、节假日等这些弱影响因素的比重，能够使预测精度得到一定的提升。

表3 考虑KPCA 前后的预测结果Table 3 Prediction results before and after considering KPCA

6.3.3 单一负荷预测与多元负荷预测对比分析

为体现多元负荷预测的优势，进行单一负荷预测与多元负荷预测结果对比如表4 所示。由于单一负荷预测下，各种负荷独立预测，相比于多元负荷预测需要耗费将近3 倍的时间成本；同时观察预测误差值可知，多元负荷预测的精度更高，结合附录A表A2 相关性量度可知，IES 中电、冷、热负荷均为对方的强相关影响因素，使模型能够更好地学习到多元负荷的更多信息，验证了IES 负荷预测时采用多元负荷预测方法的优越性。

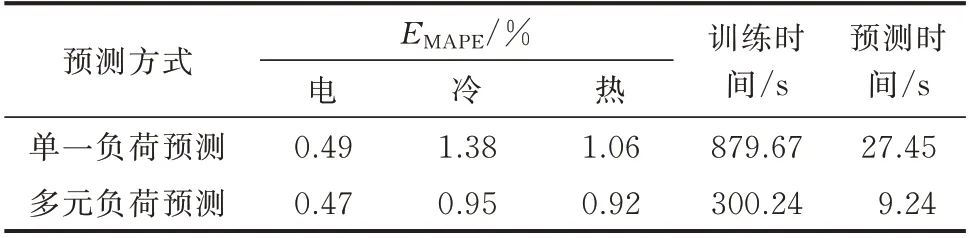
表4 单一负荷预测与多元负荷预测结果Table 4 Results of single load prediction and multiple loads prediction

6.3.4 不同预测模型对比分析

为验证本文所提出的模型能够有效提高多元负荷的预测精度，将本文所提的KQDM 预测模型与几种模型进行对比，对照模型为:反向传播神经网络组合高斯过程回归（BP-GPR）［26］；KPCA 组合深度信念网络（KPCA-DBN）；集合经验模态分解组合门控循环单元、MLR（EEMD-GRU-MLR）［18］；将本文所提KQDM 模型内DBiLSTM 神经网络替换成LSTM 神经网络（KQLM），实验结果如图5 和表5所示。

表5 不同模型预测结果Table 5 Prediction results of different models

图5 不同模型的电、冷、热负荷预测结果Fig.5 Prediction results of electric, cooling and thermal load of different models

结合实验结果可知，本文所提出的预测模型在预测精度上均高于其他4 种模型，电、冷、热负荷的预测误差EMAPE仅为0.47%、0.95%、0.92%。其中，EEMD-GRU-MLR 组合模型表现最差，EMAPE分别达到了3.36%、10.47%、4.46%，比本文模型分别高出7 倍、11 倍、4.8 倍；浅层神经网络结合统计学方法的BP-GPR 在面对随机波动性相对较大的时间序列表现也不佳；另外，近年来比较流行的深度信念网络结合KPCA 相较于上述2 种模型虽然预测精度有所提高，但EMAPE也比本文模型分别高出5 倍、6 倍、4 倍左右；而相较于上述3 种模型而言，KQLM 模型由于结合了QMD 方法的优势，在预测精度上有了较大程度的提高，但预测精度还是低于本文模型。

表5 还提供了不同模型的训练、预测时间。其中，BP-GPR 由于模型结构相对简单，因此训练时间最短，仅为94.67 s；由于EEMD-GRU-MLR、KQLM与本文所提KQDM 模型需要对分解后的非平稳分量运用神经网络进行预测，因此时间相对更长；而KPCA-DBN 的训练时间最长，已经达到了449.76 s。值得一提的是，如果本文模型仅考虑采用QMD、KPCA、DBiLSTM 而不采用MLR 对平稳分量进行预测，由于DBiLSTM 耗费时间较长，该方法下最终训练的时间成本将远高于1 h。

对上述结果进行进一步分析，结论如下。

1）EEMD-GRU-MLR 组合模型虽然采用了门控循环单元，能够在时间序列预测上取得较好的结果，但由于集合经验模态分解引入了白噪声叠加在原始序列上，导致所有IMF 重构后不等于原始序列，预测精度受到较大的影响。

2）BP-GPR 组合模型中，反向传播神经网络在训练时容易陷入局部最优，并且容易出现梯度消失等问题，而高斯过程回归也只适用于预测平稳序列，对此类非平稳序列难以准确预测。

3）KPCA-DBN 组合模型中，深度信念网络是由底层多层受限玻尔茨曼基和顶层反向传播神经网络组成，结构内部缺乏类似于LSTM 神经网络的记忆结构，性能上略差于LSTM 神经网络。

4）KQLM 模 型 采 用LSTM 神 经 网 络，结 合QMD 方法降低了预测难度，在预测精度上有了较大的提高，但由于LSTM 神经网络只对历史数据进行单向训练，没有学习到历史数据的全局信息，忽略了前后时间的关联性，因此性能略差于DBiLSTM神经网络。

而相对上述4 种模型而言，本文所提的KQDM模型运用DBiLSTM 神经网络，通过对历史数据进行双向训练，更加详细地学到历史数据包含的全局信息，并结合MLR 在平稳序列预测上的优势，在前期运用KPCA 和QMD 情况下，取得较好的预测结果。

7 结语

本文针对用户级IES 多元负荷随机、波动性相对较强的特点，提出一种KQDM 预测模型。该模型运用QMD 和KPCA 方法分别实现多元负荷模态分解和特征集降维，在简化模型的同时将多元负荷序列分解为多个更平稳的序列进而降低预测难度；然后，分别运用DBiLSTM 神经网络对历史数据进行双向训练，更好地学习到历史数据的整体信息，并运用MLR 对平稳分量进行预测，在保证预测精度的同时大大降低了预测时间。同时，本文提出一个性能较优的综合能源系统多元负荷预测组合模型，主要创新在于首先构建合适的QMD 方法对负荷序列进行二次分解，降低预测难度，然后对分解后的非平稳、平稳分量分别运用DBiLSTM 神经网络、MLR进行预测，提高预测精度的同时大大减少时间成本。

后续工作可以在本文基础上，然后考虑价格等因素，合理选择特征集。此外，由于数据在保存过程中可能会产生坏数据，在训练之前对坏数据进行辨识处理也值得进一步研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。