风电并网系统次同步振荡监测装置优化配置方法

王 杨，宋子宏，占 颖，李卓城，杜文娟，肖先勇

（1. 四川大学电气工程学院，四川省成都市610065；2. 清华大学电机工程与应用电子技术系，北京市100084）

0 引言

近年来，新能源的大规模接入显著改变了电力系统的阻尼特性与动态行为，带来了新的稳定问题。其中以风力发电引发的次同步振荡事故最为突出:2009—2017 年间，美国得克萨斯州ERCOT 地区发生多起次同步振荡事故，造成大量风机脱网和撬棒电路损坏［1-3］；2011 年以来，中国河北沽源地区风电系统发生了上百起次同步振荡事故，致使大量风机脱网以及变压器异常振动［4-6］。

现有的广域测量系统（wide-area measurement system，WAMS）和数据采集与监控（supervisory control and data acquisition，SCADA）系统，主要面向工频稳态运行数据，难以满足次同步振荡监测的需求［7-9］。为此，中国新疆等地已在近期开始对同步相量测量装置（synchrophasor measurement unit，PMU）进行改造使其具备记录次同步振荡波形的能力，本文称之为次同步相量测量装置（subsynchronous phasor measurement unit，SPMU）。风电引发的次同步振荡具有广域传播特性，理想条件下须在系统多个节点装设SPMU，从而实现次同步振荡的全景展示［10-13］。但考虑到时间和成本上的限制，短时间内在所有节点安装监测装置是不现实且不经济的。因此，研究SPMU 的最优配置，合理选取配置点对于次同步振荡的监测、溯源、抑制等均具有重要意义。

当前，有关监测装置优化配置的研究主要面向PMU，致力于在保证系统全局可观的基础上使得监测装置的数量最少，通常运用数值算法和智能算法进行求解。数值算法包括穷举法和整数规划法［14-16］，其中穷举法在节点较少的系统中简单、有效，但在应用于大系统时效率太低，且易出现遗漏。整数规划法则较为成熟，如文献［14］基于整数规划算法构建节点邻接矩阵进行求解，文献［15］提出了通过更新邻接矩阵的改进0-1 整数规划算法。智能算法包括遗传算法［17-18］、模拟退火法［19-20］等。文献［18］提出了基于改进自适应遗传算法的多阶段优化配置方法；文献［19］通过缩小模拟退火法的优化范围提高了算法求解速度。

与PMU 相似，SPMU 的配置目标同样是风电系统全局可观，进而实现振荡传播的全景展示与分析［21］。然而与PMU 配置不同的是，SPMU 在满足全局可观的条件下应额外考虑配置结果对振荡监测、溯源、控制的影响。对振荡监测而言，监测装置应优先安装在振荡可观性较强的节点；对于振荡溯源，则应优先监测呈现负阻尼的关键风电场。另外，考虑到故障易引发次同步振荡［22］，须计及N-1 故障对SPMU 配置结果的影响。

本文以大规模风电-串补系统为例，研究SPMU 的最优配置问题。以振荡监测、溯源为出发点，从可观性、阻尼影响程度两个角度定义了节点关键度。进一步，为保证N-1 故障下监测系统的可靠性，提出了计及N-1 故障发生概率和节点关键度的SPMU 最优配置方法。对美国得克萨斯州ERCOT 系统、改进的New England 39 节点系统和河北沽源实际风电并网系统不同配置方案进行分析对比，验证了本文提出方法的有效性和经济性。

1 节点关键度

本章首先利用矢量拟合法建立风电机组的阻抗模型（s域），再从振荡监测和溯源两个角度分别提出了两个评价指标探究各节点的关键程度，最后利用阻抗网络模型对这两个指标进行数学求解。

1.1 矢量拟合法

本文利用矢量拟合法建立风电机组的阻抗模型，用于后续节点关键度指标计算。基本步骤包括:通过仿真或实验获得风电机组频率响应，再利用矢量拟合法获得风电机组的输出阻抗表达式。其中，阻抗测量可通过注入扰动实现［23-25］，这里不做赘述，本文重点阐述阻抗拟合方法，即矢量拟合法［26］，其原理是将离散频率响应拟合为传递函数f（s）:

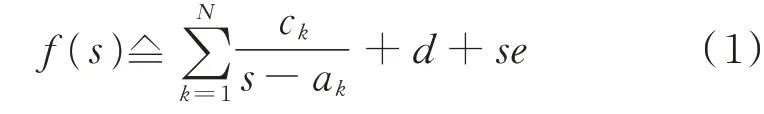
式中:ck、ak分别为f（s）的第k个留数、极点；d、e为实系数；N为传递函数阶数。

设置一组初始极点a0，k并构建辅助函数σ（s）:

式中:上标T 表示取矩阵的转置。通过最小二乘法求解即可得到σ（s）的留数:

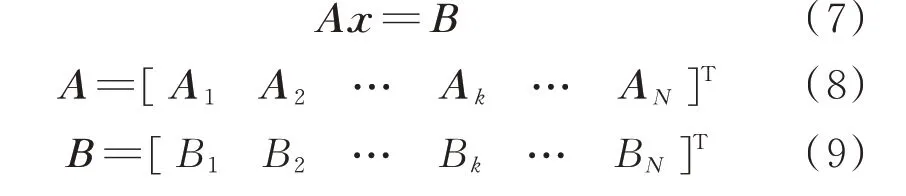
上述公式仅适用于实极点，对于复极点需要进行修正以保证留数为共轭级数对。假设i和i+1 是一对共轭极点，即

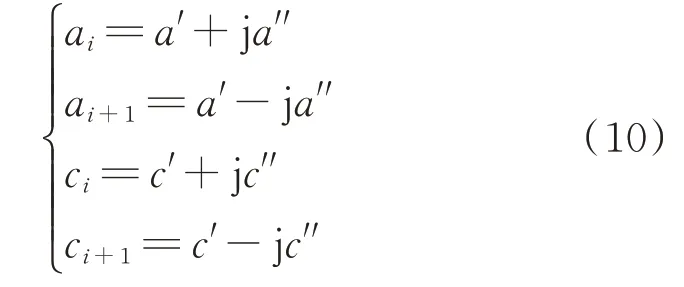
式中:a′、a′′分别为共轭复数ai、ai+1的实部、虚部；c′、c′′分别为共轭复数ci、ci+1的实部、虚部。

对应地，Ak，i、Ak，i+1应修改为:

式中:ai*表示取复数ai的共轭。

数学上，式（2）可以改写为:

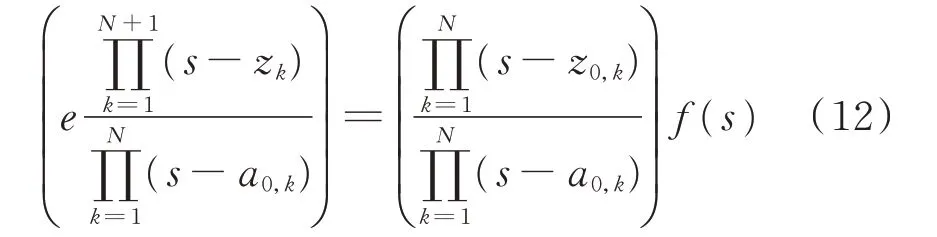
式中:zk和z0，k为对应函数零点，后者可通过式（13）求得。

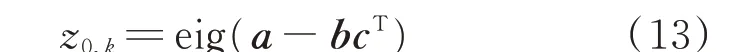
式中:eig（a-bcT）表示求解矩阵（a-bcT）的特征值；a、b、c可 通 过σ（s）计 算 求 得，具 体 公 式 可 参 见 文献［27］。

由式（10）可知，等式两端初始极点a0，k相互抵消，z0，k成为新的极点，重复上述过程直到收敛，即可求得极点ak。进一步，可通过如式（7）所示最小二乘法得到d、e，其中Bk和式（6）相同，Ak和x变为:

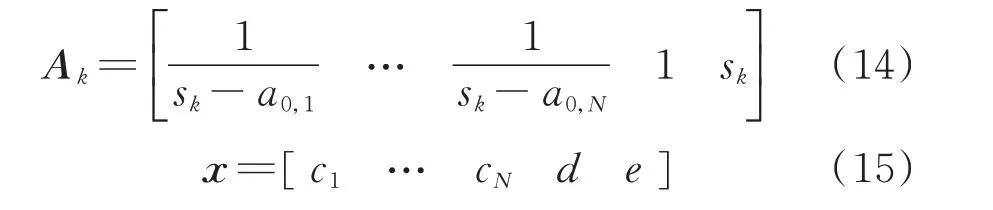
通过上述方法即可获得风电机组以及其他黑盒模型的输出阻抗表达式。

1.2 可观性指标

如果某一振荡模态能够被节点观测，则称该模态是可观的。考虑到不同节点对振荡观测效果存在差异，需进一步定义节点对振荡模态的可观性指标，该指标对于振荡监测、预警具有重要意义。本文作者在既往工作中提出了基于回路阻抗矩阵的可观性分析方法［28-29］，这里做简单回顾。

假设在支路h施加单位脉冲扰动电压，其在支路l所激发的电流为:

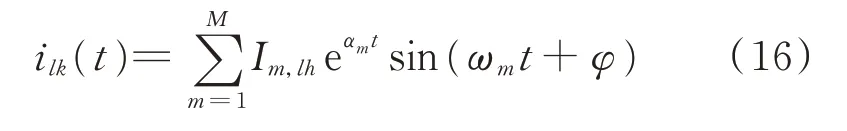
式中:Im，lh、αm、ωm、φ分别为振荡模态λm下的支路电流幅值、衰减因子、角频率、初相角；M为振荡模态数量；l=1，2，…，NL，NL为支路总数。

定 义 支 路l的 可 观 性 指 标om，l为:振 荡 模 态λm下，在支路h施加单位脉冲扰动电压后，在支路l观测到的相对电流幅值，如式（17）所示。进一步，定义节点n可观性指标om，n为:节点n所连接支路的可观性指标总和的相对大小，如式（18）所示。该指标越高，说明振荡发生时节点n能够观测到的振荡分量幅值越高，对振荡监测、预警越有意义。

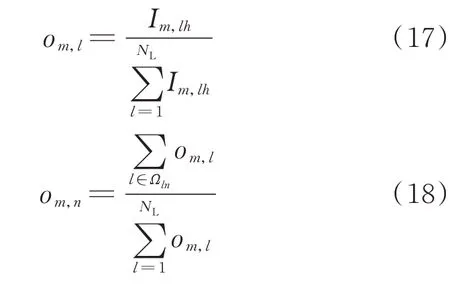
式中:Ωln为节点n的邻接支路集合。

对于任意系统，其小信号动态方程表示如下:

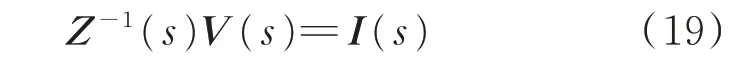
式中:Z（s）为s域回路阻抗矩阵，该矩阵包含上一节中利用矢量拟合得到的风电机组阻抗模型；V（s）为回路电压向量；I（s）为回路电流向量。

通过求解回路阻抗矩阵行列式为零的解:可得到系统振荡模态:λm=σm±jωm。

对于一个给定的振荡模态λm，由于回路阻抗矩阵Z是对称的，故可以表示为:

式 中:Λ为 特 征 矩 阵；H和W分 别 为 左、右 特 征矩阵。

Z（s）的行列式为零，即Λ中存在一个为零的特征值，将μp看作一个无限接近于零的数，根据式（21），Z-1（λm）可以表示为:

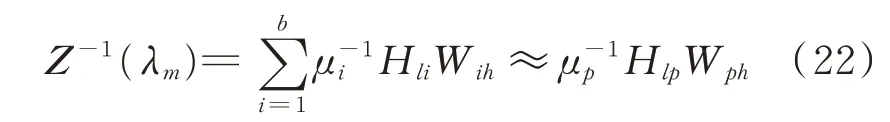
式中:b为独立回路数；μi为矩阵Z第i个特征值。

由式（19）、式（21）可得支路电流与注入扰动电压之间的关系为:

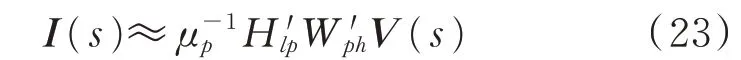
式中:H′lp和W′ph分别为矩阵H′和W′第l行第p列、第p行第h列的元素。变化后的矩阵H′、W′可利用回路-支路关联矩阵B求得:

故施加单位脉冲扰动电压所激发的支路电流为:

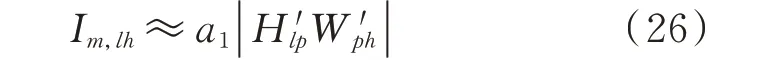
式中:a1为非零常数。

代入式（17）可得到振荡模态λm下支路l的可观指标的计算式为:

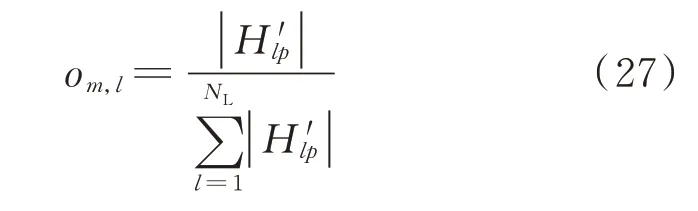
由式（27）可知，振荡可观性指标仅与左特征向量H有关，因此利用回路阻抗矩阵以及特征值分解即可快速计算可观性指标。

1.3 阻尼影响指标

近年来研究已从理论与工程上证实风电次同步振荡问题多由风力发电机提供负阻尼引发［30-32］，因此从溯源的角度考虑，呈现负阻尼的关键风电场应优先监测。另外，考虑到火电机组和柔性无功补偿装置如静止同步补偿器（STATCOM）、静止无功发生器（SVG）等也具备引发次同步振荡的可能性［33-35］，其阻抗特性同样需要被测量。本文定义节点阻尼灵敏度为节点阻抗变化10%时引起的系统阻尼变化量。该指标反映了风机等潜在振荡源对振荡模态的影响程度，指标越高说明阻抗调节对振荡抑制效果越明显，对振荡溯源、抑制越有意义。

定义节点j的阻尼影响指标dj为:节点j阻尼灵敏度绝对值的相对大小，即

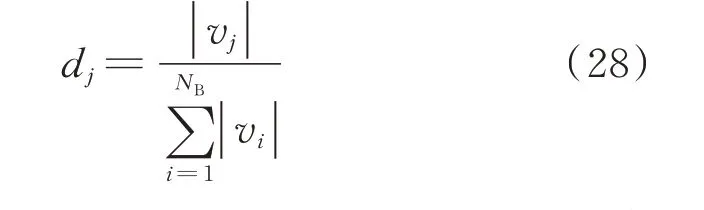
式中:vj为节点j阻尼灵敏度；NB为系统节点数。值得注意的是，本文节点阻尼灵敏度计算仅针对连接潜在振荡源的节点，其他节点阻尼灵敏度为零。

1.4 节点关键度指标

在获得可观性指标、阻尼影响指标之后，通过加权获得节点关键度指标（nodal critical index，NCI），其中可观性指标权重代表振荡监测重要性，而阻尼影响指标权重代表振荡溯源重要性。本文设定两者权重相同，不同工况间以阻尼大小为权重进行加权计算，进而求得计及不同工况的节点关键度指标。值得注意的是，系统同一工况下具有多个振荡模态，本文仅选取具有振荡风险的模态进行分析计算。

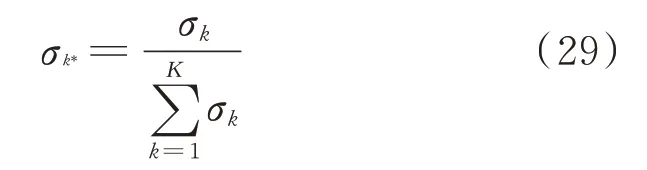
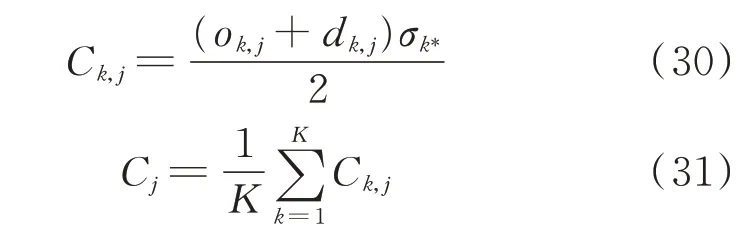
式 中:σk为 第k个 工 况 下 的 阻 尼；σk*为 该 工 况 权 重；ok，j、dk，j、Ck，j分 别 为 第k个 工 况 下 节 点j的 可 观 性 指标、阻尼影响指标、关键度指标；K为工况数量；Cj为节点j的关键度。

2 SPMU 最优配置模型

对含有NB个节点、NL条线路的系统，以节点关键度指标为节点权重，全局可观为约束条件，可建立如式（32）所示的SPMU 配置模型。优化目标包括布置SPMU 的节点最少以及关键度最高，分别由目标函数的第1 项和第2 项体现；约束条件保证了风电系统具有全局可观性，即节点本身或与其相邻的节点中至少有一个节点配置SPMU。

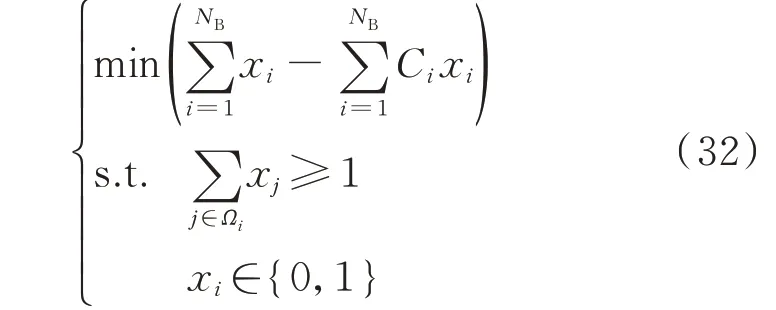
式中:xi为0-1 决策变量，xi=0 表示在节点i不布置SPMU，xi=1 表示在节点i布置SPMU；Ωi为节点i的邻接节点集合（包括节点i本身）。

2.1 计及N-1 故障概率的最优配置模型

考虑到线路故障易引发次同步振荡且可使系统失去全局可观性，需对式（32）改进，提出计及N-1故障的SPMU 最优配置模型以提高监测系统的可靠性。首先确定各线路断线概率［36-37］:

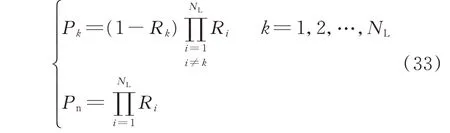
式中:Pk为线路k的断线概率；Pn为系统正常运行的概率；Rk为线路k的可靠性。

Rk通过线路故障率和修复率确定［38］:

式中:λ、μ分别为线路k的故障率、修复率。

为最大限度地提高监测系统的可靠性，将式（32）中的目标函数扩展为:

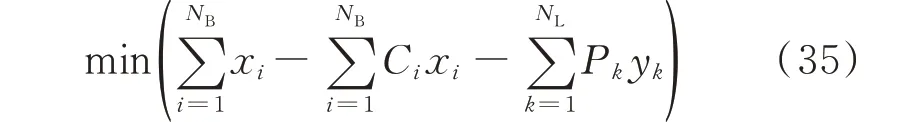
式中:yk为观测变量，yk=0 表示系统在线路k断线的情况下无法保证全局可观，yk=1 表示系统在线路k断线故障下仍能保证全局可观。目标函数第3 项的目的在于使系统不受N-1 故障影响的概率最高。

还应对线路送、受端增加如式（36）、式（37）所示的约束条件，以满足断线情况下的可观性要求。

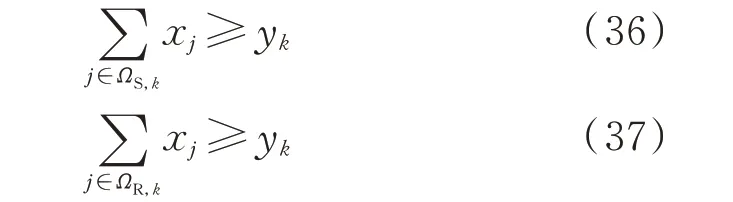
式中:ΩS，k为线路k断线后送端母线邻接节点集合（包括送端节点本身，不包括受端节点）；ΩR，k为线路k断线后受端母线邻接节点集合（包括受端节点本身，不包括送端节点）。

yk=1 时，相当于对断线后送、受端母线分别加以约束以保证可观，从而使得全局可观性不受线路k断线影响。如图1 所示，正常工况下只需在节点2配置SPMU 即可使得全局可观。线路2-3 故障下在节点3 加装SPMU 才能满足约束条件，从而保证全局可观性不受其影响。

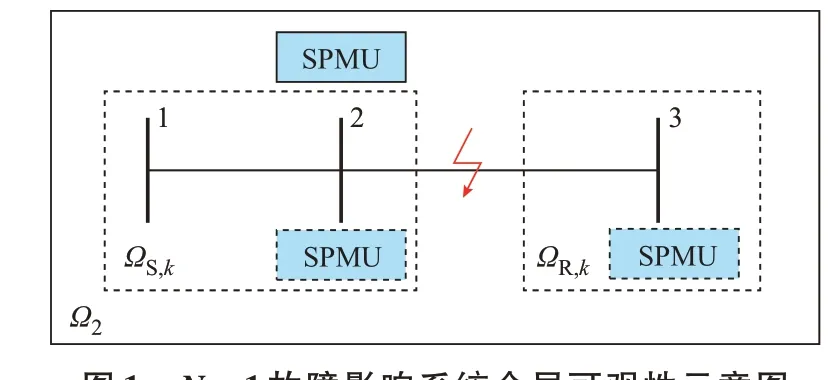
图1 N-1 故障影响系统全局可观性示意图Fig.1 Schematic diagram of impact of N-1 contingency on system global observability

考虑到监测系统可靠性越高，所需SPMU 的数目也越多，为满足对监测系统经济性与可靠性的不同需求，引入监测系统可靠性Rwd，并要求正常运行和N-1 工况下系统全局可观的总概率不小于Rwd，即

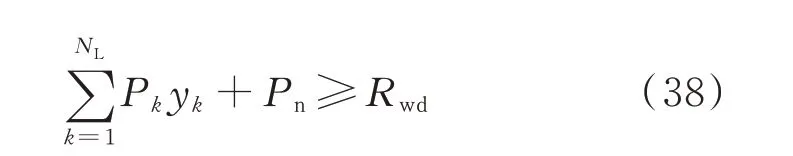
Rwd反映了对系统不受N-1 影响保持全局可观的最低概率要求。较高的Rwd使得系统应对多种N-1 故障均能保证全局可观。随着Rwd的降低，系统对N-1 故障的应对能力减弱。

2.2 零注入节点的影响

在本文问题中，零注入节点是指没有与风电机组、发电机等可变阻抗相连接的节点。在实际应用中，若考虑下列零注入节点规则，将有效减少SPMU 配置的数量［39-40］。

1）与零注入节点邻接的节点中只有一个节点不可观测时，可以通过在零注入节点应用基尔霍夫电流定律（KCL）实现对该节点的观测。

2）当零注入节点不可观测而其相邻节点均可观时，可以应用KCL 实现对零注入节点的观测。

考虑零注入节点后，若不计及N-1 故障，式（32）中约束条件可更改为:

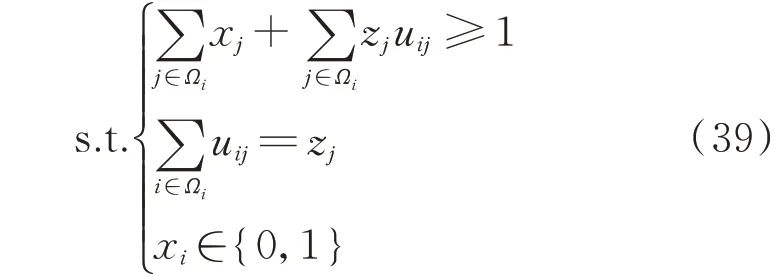
式中:zj=0 表示节点j为非零注入节点，zj=1 表示节点j为零注入节点；uij为辅助变量。

对于计及断线概率以及零注入节点的SPMU最优配置问题，可以建立如式（40）所示的模型，通过整数线性规划求解得到SPMU 配置方案。

式中:uk，ij为线路k断线下的辅助变量。

3 算例分析

本文采用美国得克萨斯州ERCOT 系统、改进的New England 39 节点系统和中国河北沽源实际风电并网系统验证所提算法的有效性和经济性。

3.1 ERCOT 系统

该系统拓扑结构如图2 所示，图中风电场WF1、WF2、WF3、WF4、WF5 风机台数分别为430、350、380、300、380，节点5、6 间装有串联补偿，补偿容量为25%。

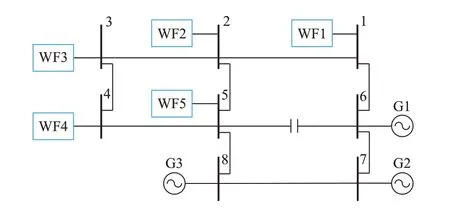
图2 ERCOT 风电系统Fig.2 ERCOT wind power system

各线路可靠性及断线情况下的系统振荡模态如表1 所示。

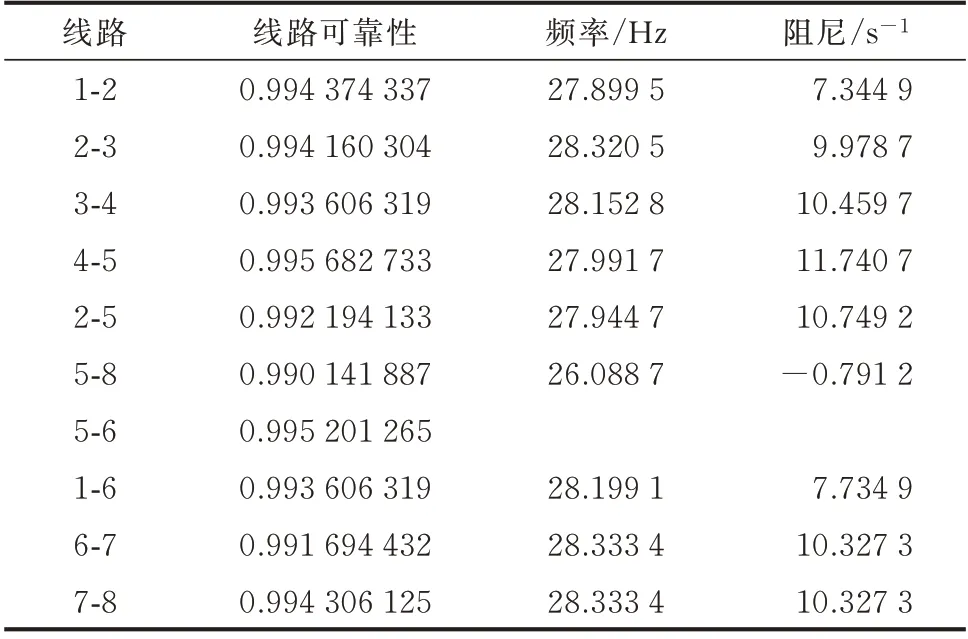
表1 各线路可靠性及断线情况下的振荡阻尼和频率Table 1 Reliability of each line and oscillation damping and frequency in case of disconnection

由表1 可知，只有在线路5-8 断线时才会引发次同步振荡，因此只需计算该故障下各节点关键度指标。需要指出的是，本文利用风机内部参数构建系统状态空间模型，求得特征值与表1 一致，验证了矢量拟合所得振荡模态的准确性。因篇幅有限，验证细节不做赘述。利用第1 章所述方法计算可观性指标和阻尼影响指标，结果见附录A 表A1 和表A2。注意到系统只有在线路5-8 断线时对应阻尼为负，因此该工况权重为1。在PSCAD/EMTDC 中搭建图2 所示系统的电磁暂态模型，并在10 s 时断开线路5-8 引发次同步振荡，振荡电流波形见附录A 图A1。通过对比表1 与图A1 所示的时域分析结果，进一步证明了振荡模态计算的准确性。同时，记录各支路振荡电流并对其进行标幺化处理，验证了各支路可观性指标的准确性，结果见附录A 表A3。

根据式（29）、式（30）可得节点关键度指标，如表2 所示。根据表1 及式（33）、式（38）可得Pn为93.68%，Rwd的 最 大 取 值 为99.82%。 以Rwd取93.68%为例，求得计及节点关键度的SPMU 最优配置方案，并与未考虑系统节点关键度模型求解的结果进行对比，对比结果如表3 所示。由表3 可知，本文所提方法能够将监测装置优先配置在更为重要的节点上，且未增加所需SPMU 数目。例如，节点5连接了串补电容，在此节点能更好地监测由串补电容和风电场相互作用产生的振荡；此外，节点5 的阻尼影响指标高，说明WF5 对振荡模态的影响较大。

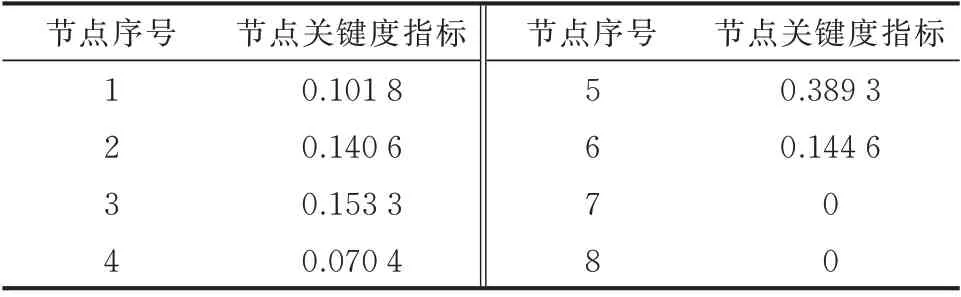
表2 ERCOT 风电系统的节点关键度指标Table 2 NCI of ERCOT wind power system

表3 SPMU 配置情况Table 3 SPMU placement

3.2 改进的New England 39 节点系统

第2 个案例验证基于New England 39 节点系统，分别在节点4、5、7、8、16、17、18、26、27 设置风电场WF1～WF9，在线路4-5、17-27 分别设置串补电容，系统拓扑结构如图3 所示。

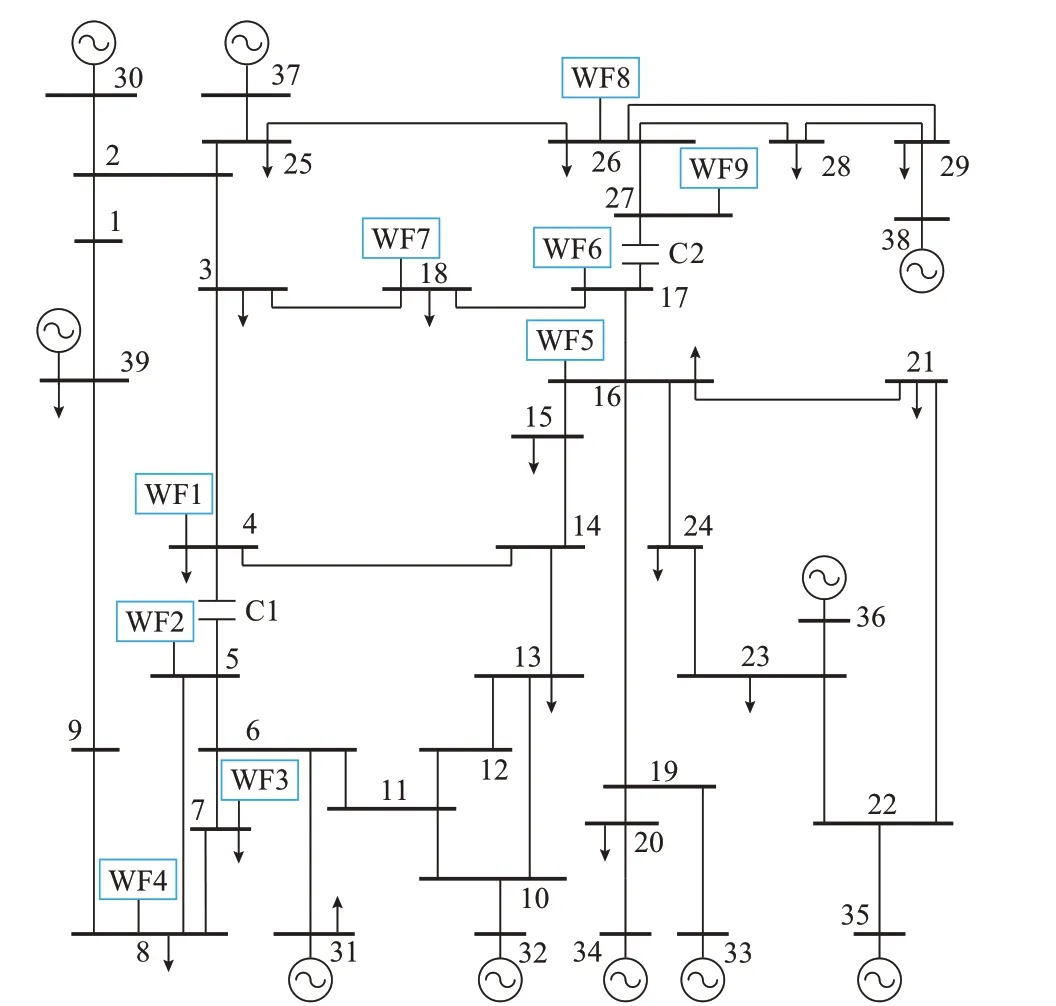
图3 改进的New England 39 节点系统Fig.3 Modified New England 39-bus system

为探究系统在不同工况下的次同步振荡风险，本文考虑3 种风速条件（7、8、9 m/s）、3 种风机出力方案、3 种串联补偿方案以及46 种N-1 故障情况，设置了总计1 242 个测试场景，其中222 个场景存在次同步振荡风险。对具有次同步振荡风险的工况，以负阻尼大小为权重进行加权计算，求得系统各节点关键度指标，如图4 所示。补偿容量及风机出力方案分别见附录A 表A4、表A5。各工况权重见附录A 图A2。

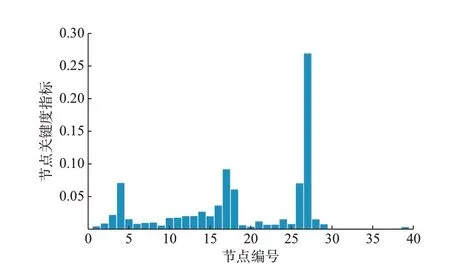
图4 改进的New England 39 节点系统的节点关键度指标Fig.4 NCI of modified New England 39-bus system

改进的New England 39 节点系统各线路可靠性见附录A 表A6，根据式（33）、式（38）得到Pn为75.00%，Rwd的最大取值为96.65%。

为验证本文算法的优越性，将本文算法与文献［37］算法（未计及节点关键度、零注入节点）进行对比，对比结果如表4 所示。可见，本文提出的算法在利用零注入节点减少SPMU 数量、提高经济性的同时，优先将SPMU 配置在更为重要的节点。

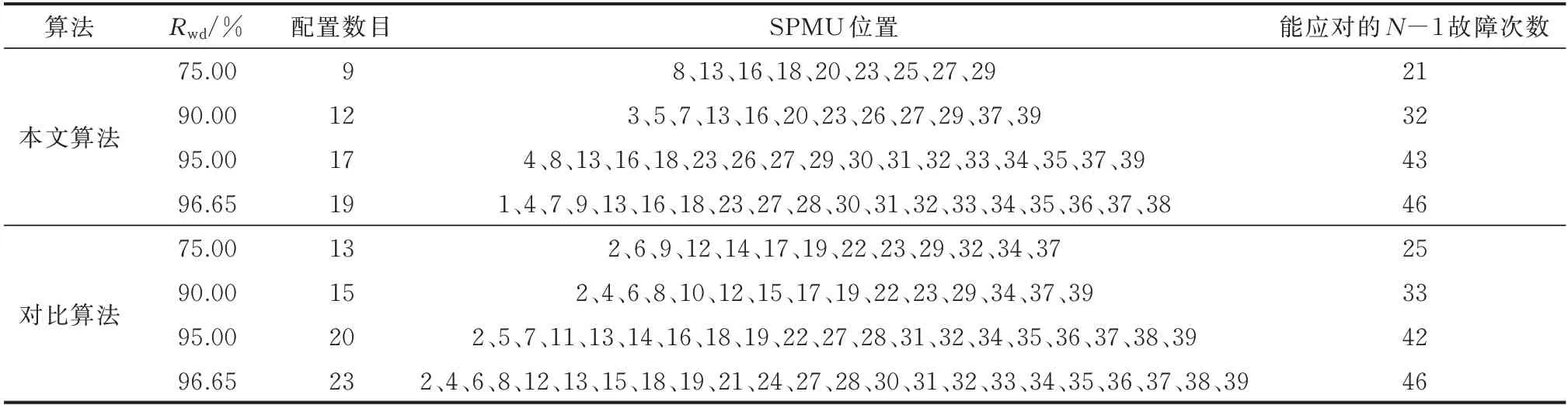
表4 不同算法下的SPMU 配置情况Table 4 SPMU placement in different algorithms

以节点27 为例，本文算法在配置SPMU 数量较少的情况下（Rwd取75.00%和90%时）仍保证了该节点的优先监测。该节点阻尼影响指标最高，说明风电场WF9 的阻尼对于振荡模态具有重要影响，应重点监测用以振荡溯源。另外，由于该节点连接串补电容C2，可观性指标也最高，能够更好地监测由风机和串补电容交互作用引发的次同步振荡。对比算法因未考虑节点关键度，所以没有选择监测节点27。通过观察不同Rwd下SMPU 的数量可知，随着系统可靠性要求的提高，SPMU 的数目也相应增加。这使得决策者可以综合经济性与可靠性要求选择更为合适的SPMU 配置方案。

3.3 工程应用

工程应用验证基于实际发生过次同步振荡事故的中国河北沽源风电系统［41-42］，合理简化后如图5所示。系统共有7 座风电场、12 个节点，总装机容量约为3 000 MVA。各风电场电能经辐射状网络汇集至沽源变电站，而后经两条500 kV 串补线路输送至主网，固定串联补偿器（fixed series compensator，FSC）补偿容量分别为40%、45%。各风电场风机台数、线路长度见图5，线路参数见附录A 表A7。系统存在频率约为7 Hz 的振荡模态，本文以此为背景计算各节点关键度指标，进一步求解SPMU 配置方案。

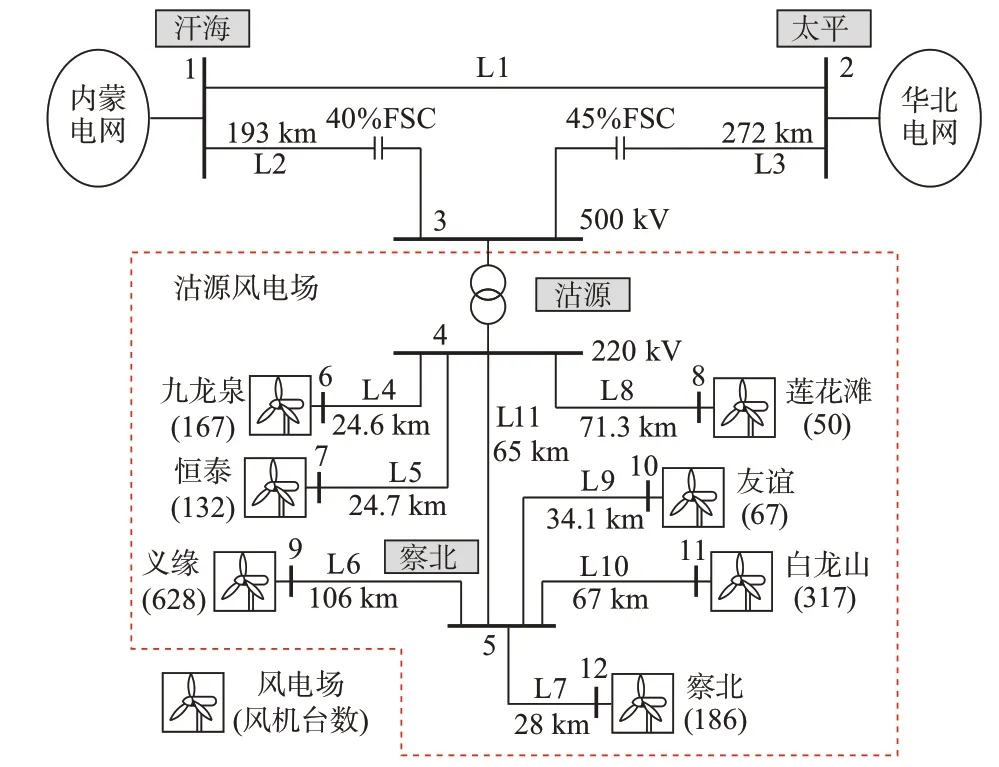
图5 中国河北沽源风电系统Fig.5 Wind power system in Guyuan,Hebei Province, China

通过第1 章中所述方法计算得到节点关键度指标，如表5 所示。系统各线路可靠性见附录A 表A8，根据式（31）、式（36）得到Pn为96.05%，Rwd的最大取值为99.93%，求得SPMU 最优配置结果如表6所示。

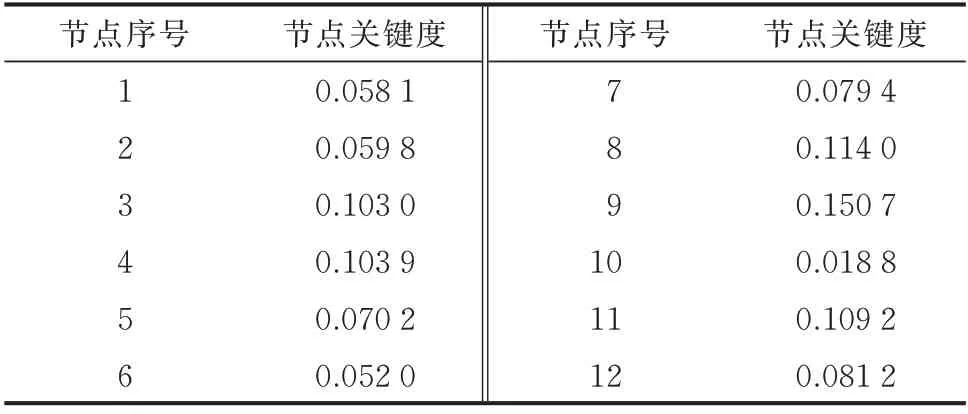
表5 中国河北沽源风电系统节点关键度指标Table 5 NCI of wind power system in Guyuan,Hebei Province, China

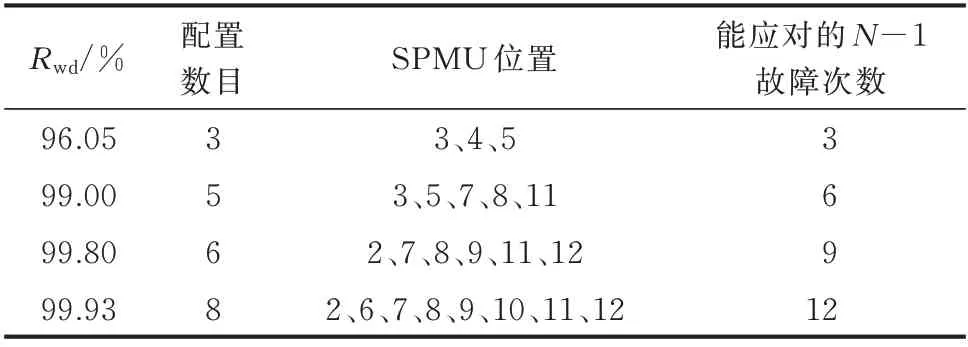
表6 不同可靠等级下的SPMU 配置情况Table 6 SPMU placement with different reliability levels

由表6 可知，当Rwd要求较低时，可在汇集场站配置，如节点4、5 配置监测装置，从而实现振荡全局可观。随着Rwd升高，在汇集场站安装SPMU 不利于N-1 故障下系统可观，应更多地在非汇集关键节点安装，从而提高监测可靠性。例如，Rwd从96.05%提高到99.93%时，通过在与汇集场站（节点4）的邻近节点（节点6、7、8）配置SPMU，使得全局可观性不会受该节点到汇集场站间线路（L4、L5、L8）发生N-1 故障的影响，而汇集场站也可通过其他邻近节点配置的SPMU 间接观测，不必再配置SPMU。

4 结语

本文针对风电并网带来的次同步振荡问题提出了完整的监测装置配置方法。首先，从振荡监测和溯源两个角度提出了节点关键度指标，保证SPMU配置在更为关键的节点；其次，建立了计及N-1 故障概率和零注入节点影响的SPMU 配置模型，最大化减少监测装置数量并提升监测系统应对故障的能力；继而以目前频发的风电-串补系统次同步振荡问题为例，依托美国得克萨斯州ERCOT 系统、改进的New England 39 节点系统和中国河北沽源实际风电系统对不同配置方案进行分析对比，验证了算法的可靠性和经济性。

本文节点关键度指标的计算基于风电机组的一维阻抗模型，未计及次、超同步频率耦合效应。在后续的研究中将考虑频率耦合效应，进一步研究更为完善的节点关键度指标计算方法。同时，本文提出的优化配置方法有望推广应用至其他振荡问题，如大规模风电经直流外送系统的宽频振荡监测，相关工作正在积极开展。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。