基于成像高度计数据的系统姿态误差估计❋

刘宗林， 王运华,2❋❋， 赵朝方,2

(1. 中国海洋大学信息科学与工程学院， 山东 青岛266100； 2. 青岛海洋科学与技术试点国家实验室， 山东 青岛 266237)

成像高度计海面测高数据所具有的高分辨、宽刈幅特征，使其在亚中尺度海洋现象观测领域具有广泛应用前景。成像高度计平台姿态误差是影响成像高度计海面测高数据精度的重要因素，主要包括平台高度误差和基线倾角误差。1973年，美国宇航局(NASA)发射的天空实验室(Skylab)搭载了首台传统雷达高度计(S-193)，其成功发射和运行验证了利用高度计观测海洋的可行性[1]。此后，卫星高度计不断发展,测高精度得到了显著提高。目前，高度计的类型有三种：传统雷达高度计、合成孔径雷达高度计和成像雷达高度计。其中，传统雷达高度计的测高精度可以达到厘米级，其数据产品能够满足中尺度(>100 km)的海洋现象的研究。与传统雷达高度计相比，合成孔径雷达高度计能获得更高的沿轨向分辨率和更多的有效观测视数，进而提高海面高度的测量精度[2]。但是，受限于一维采样特性，传统雷达高度计数据和合成孔径雷达高度计数据空间分辨率低于百公里，无法支持亚中尺度(<100 km)的海洋现象的研究[3]。海洋中约50%的营养物质垂直传输发生在亚中尺度(10～100 km)[4]。亚中尺度下，能量非线性传递对理解海洋环流的能量平衡具有重大意义[5]。为了实现亚中尺度海洋现象观测，Rodrigueze等于1999年提出了宽刈幅海洋高度计的概念[6]，其突破一维采样特性的局限，通过二维采样将空间分辨率提升至几公里。目前，国外对于成像高度计(Imaging Altimeter IA)的研究以NASA提出的SWOT任务为代表[7-8]，SWOT将搭载Ka波段的干涉成像雷达高度计[9-12]，其数据产品主要应用于内陆水体动态变化和亚中尺度海洋涡旋检测。国内对IA的研究以天宫二号搭载的Ku波段的三维成像微波高度计为代表，其成功运行验证了三维测高的可行性[13]。为了实现成像高度计数据化应用，青岛海洋科学与技术试点国家实验室提出了“观澜号”任务[14]。“观澜号”将搭载双频(Ka和Ku波段)成像高度计，计划获取亚中尺度海表高度数据。成像高度计作为一种新兴高度计，其观测数据空间分辨率高、覆盖范围广，对于误差的敏感度也更高，这些误差将会极大地影响测高精度。因此，为了获得高精度的测高数据，成像高度计需要严格的误差控制。

成像高度计的误差主要包括三大类：大气传输误差[15-16]、随机误差[17-18]和系统姿态误差[19-20]。其中，系统姿态误差对测高精度的影响十分严重，包括：基线倾角误差、基线长度误差、平台高度误差。成像高度计的误差补偿可以通过搭载辅助传感器(辐射计、陀螺仪等)来校正误差。因此，辅助数据的精度决定了高度数据的精度。当缺少辅助数据或辅助数据精度低时，最终的高度数据会包含较大的残余误差，无法满足研究需求。为了提高测高精度，可以从高度数据出发，利用基于数据处理的方式来估计系统姿态误差。目前，孙馨怡等提出了一种基于天底点干涉相位反演基线倾角的方法[21]，该方法可以用来估计基线倾角误差。本文根据系统姿态误差的分布规律，提出了一种基于成像高度数据的误差估计方法。该方法可以有效的实现系统姿态误差的补偿，提高测高数据精度。

1 仪器系统误差分析

1.1 成像高度计测高原理

成像高度计测高原理同干涉合成孔径雷达工作原理一样，都是通过有一定视角差的两个天线接收同一区域的SAR相干图像，然后利用干涉相位计算出高度值。成像高度计测高几何关系如图1所示。

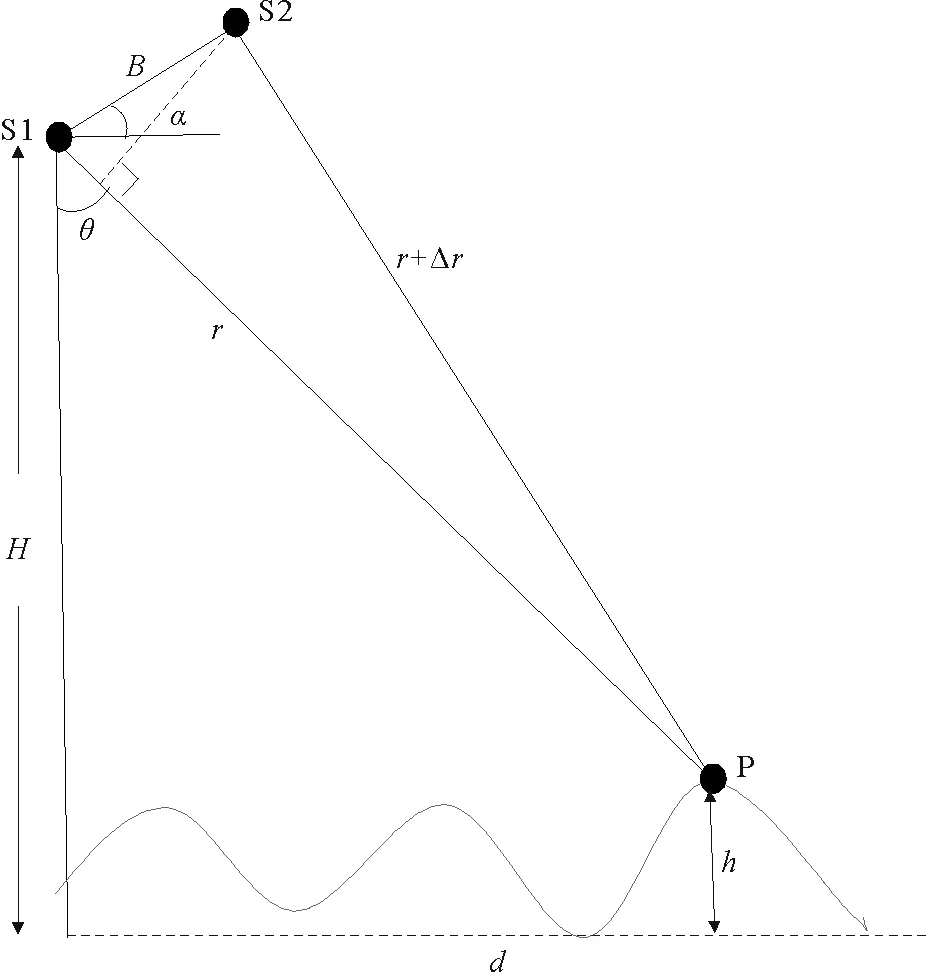
(平台高度为H,基线倾角为α，基线长度为B。S1和S2分别是天线1和天线2，位于基线两侧。对于海面高度为h的某点P，P点和天底点的距离为d,天线1和该点的距离为r，入射角为θ。天线2和点P的距离为r+Δr。The platform height is h, the baseline inclination angle is α, and the baseline length is B. S1 and S2 are antenna 1 and antenna 2, respectively, on both sides of the baseline. For a point P with sea surface height h, the distance between P point and ndir is d, the distance between antenna 1 and the point is r, and the incident angle is θ. The distance between antenna 2 and point P is r+Δr.)

对于单发双收工作模式，在理想情况下，忽略随机相位噪声的影响。天线1和天线2接收到的SAR数据如(1)式和(2)式所示:

(1)

(2)

式中：s1,s2分别表示主辅SAR回波数据；A1、A2是后向散射系数；λ是信号波长；r是斜距；Δr是路径差。将(1)、(2)式共轭相乘，得到干涉相位ø：

(3)

根据图1 所示几何关系，可以得到：

Δr≈Bsin(θ-α)。

(4)

式中：B是基线倾角；θ和α分别是入射角和基线倾角。将(4)式代入(3)式，即可得到：

(5)

因此，根据图1几何关系得到海表高度为：

(6)

1.2 系统姿态误差分析

成像高度计的误差主要分为三大类：随机误差、系统姿态误差和大气延迟误差。系统姿态误差包括：基线长度误差、基线倾角误差和平台高度误差，分别对应式(6)中的参数B、α、H。根据公式(6)，分别推导出上述三个参数的测高误差公式。

基线长度误差对测高的影响如式(7)：

(7)

基线长度误差产生原因有两个：一是对基线本身长度测量不精确产生的测量误差；二是成像高度计在测量过程中，由于热力学环境变化导致基线伸缩，从而产生了基线长度误差。因此，基线可以使用对热力环境变化不敏感的复合材料，避免基线长度大幅度变化。

基线倾角误差公式如式(8)：

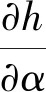
(8)

其中d是地距。

基线倾角误差是影响测高精度的主要误差之一，按照其产生原因可以分为两类：一是基线自身倾角测量不准确；二是基线横滚误差：测高平台在飞行过程中发生横滚，从而导致基线倾角变化。根据式(8)可以发现，倾角误差随地距增加而增大。对于基线倾角误差的补偿，通常使用陀螺仪测量倾角变化，根据测量值补偿倾角误差。成像高度计具有宽刈幅成像特性，其地距远端可以达到百公里，即使横滚角的测量误差为0.000 1°(0.36角秒)，在地距为100 km处的高度误差也将会达到17 cm。因此，使用仪器测量倾角误差时，其测量精度必须相当高，这是成像高度计误差处理的难点之一。

平台高度误差的影响如式(9)：

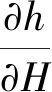
(9)

平台在测量过程中，由于平台不稳定而产生高度起伏，高度起伏直接作用于高度反演，产生高度误差。处理平台高度误差时，通常使用GPS定位测量出轨道高度的变化，然后在反演高度中减去高度起伏即可实现误差补偿。

成像高度计的系统姿态误差是影响测高精度的主要误差之一，尽管成像高度计可以通过搭载辅助仪器来进行误差校正，但是目前仪器的测量精度很难满足需求。因此，当仪器测量精度不足或缺少辅助数据时，可以基于高度数据来估计系统姿态误差。

2 误差估计和结果分析

成像高度计的误差主要包括：大气延迟误差、随机误差和系统姿态误差。假定各种误差不相干，则不同的误差可以分开处理。本文根据成像高度计系统姿态误差的分布规律，提出一种基于成像高度计数据的系统姿态误差估计方法。其中，海况会影响误差估计精度。本文将仿真不同海况下的成像高度计数据，分析不同海况的影响程度。

2.1 误差估计

成像高度计采用正侧视方式观测，其观测几何示意图如图2所示。通过发射线性调频信号，成像高度计可以获得二维高度图像。二维图像中，平台飞行方向是方位向，雷达侧扫方向是距离向，两个维度的单位都是米，表示空间位置。成像高度计在飞行过程中，同一方位向具有相同的基线长度、基线倾角和平台高度。因此，可以利用二维高度数据进行系统姿态误差估计，得到沿方位向的系统姿态变化。

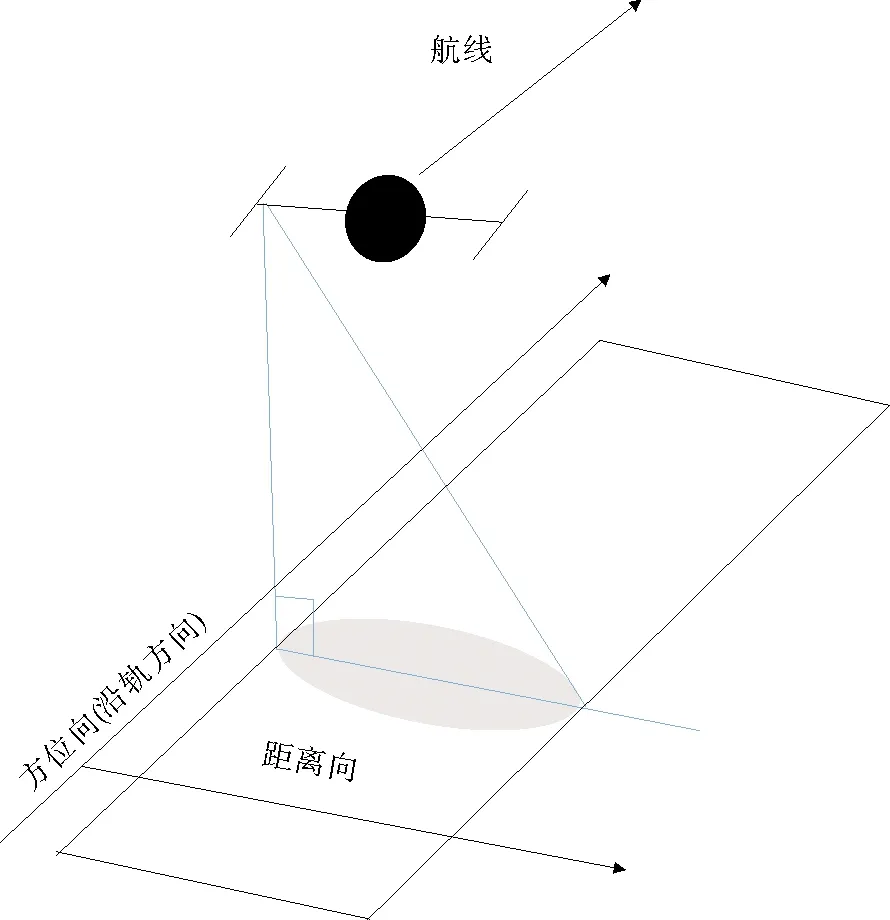
图2 成像高度计观测示意图

在实际观测中，成像高度计为了避免基线长度的较大伸缩，通常采用刚性材料制作基线。相比于基线倾角误差和平台高度误差，基线长度误差影响较小。因此，系统姿态误差主要包括基线倾角误差和平台高度误差。当同时存在基线倾角误差和平台高度误差时，系统姿态误差沿距离向的分布如(10)式。

Esys(d)=d×δα+δH。

(10)

式中:Esys是系统姿态误差；d是地距；δα是倾角误差；单位是弧度；δH是平台高度误差。根据(10)式可以看出，系统姿态误差随地距线性变化。

当海表高度数据仅包含海浪信息和系统姿态误差时，对于同一方位向，随着距离增加，系统姿态误差线性变化，而海浪分布与距离无关，具有随机性。因此，可以对同一方位向高度的线性变化进行估计，估计结果就是系统姿态误差。当海表高度数据中减去估计的系统姿态误差后，同一方位向残余的高度数据平方和体现了误差估计的准确度。假如同一方位向的海浪完全随机分布，根据最小二乘理论，当同一方位向的残余高度数据的平方和最小时，可以得到系统姿态误差的最佳估计值。实际上，海浪的分布对误差估计有一定的影响。这种影响将在后两节进行讨论。本文误差估计流程图如图3所示，主要包括两个部分：误差初值估计和最佳误差估计值确定。

图3 系统姿态误差估计流程图

误差初值估计是对系统姿态误差的粗略估计。根据(10)式，在距离向近端，基线倾角误差影响小，相比于平台高度误差可忽略。因此，可以计算距离向近端的均值，实现平台高度误差的粗略估计。然后，在海表高度数据中减去平台高度误差估计值，得到残余高度数据。残余高度数据中主要包含基线倾角误差，根据基线倾角误差与地距的关系，将残余高度数据除以地距，由高度值转化为角度值。然后对同一方位向的角度求平均，得到倾角误差估计初始值。

初始误差估计值是根据系统姿态误差分布粗略估计出的值，其值在准确估计值附近波动。反过来，误差准确估计值也在初始误差估计值附近波动。根据(10)式，系统姿态误差随距离线性变化，其斜率表示倾角误差，截距表示平台高度误差。因此，令误差初始估计值为中心，设定一个范围，在这个范围内循环产生不同的基线倾角误差和平台高度误差的组合，得到系统姿态误差估计值。然后对高度数据进行误差补偿，补偿后得到残余高度数据。对于每一个方位向行，如果当前残余高度数据平方和最小，则将当前值记录为当前最佳估计值，继续循环直到循环结束。当循环结束后，误差估计值的记录结果就是最佳估计值。

对于基线倾角误差，本文的循环范围为-0.003°～0.003°，递增量为0.000 05°；对于平台高度误差，本文的循环范围为-0.5～0.5 m，递增量为0.005 m。需要注意的是：误差的组合是通过递增来实现的，递增量的设置决定了误差估计的精度；循环范围大小决定了能否取到最佳估计值。在进行误差估计时，循环范围必须足够大，递增精度必须足够高。

2.2 海浪对误差估计的影响

在实际的海表高度数据中，海浪的分布并不完全随机。不同的海况会改变海浪分布的随机性，在一定程度上影响误差估计结果的准确性。本文将仿真不同海况下的海表高度，并对仿真数据进行误差估计，分析不同海况的影响。

2.2.1 海表高度数据仿真 本节的研究工作基于仿真的海表高度数据。仿真海表高度数据分为三步：海浪仿真、系统姿态误差仿真和海表高度数据生成。根据文献[22]，t时刻下，空间坐标为(xm,yn)点处的海浪高度如式(11)：

z(xm,yn,t)=∬ξkx,kycos(kx·xm+ky·yn-ωkx,ky·t+ψkx,ky)dkxdky。

(11)

式中kx和ky分别表示方位向波数和距离向波数坐标。海浪的角频率ωkx,ky和波数矢量(kx,ky)的关系如式(12)：

(12)

式中g是重力加速度。(11)式中，相位ψkx,ky在(0,2π)之内均匀分布，包含了风浪和涌浪的振幅ξkx,ky如式(13)所示：

(13)

式中:Swind(kx,ky)是风浪谱，采用的是Elfouhaily谱[23]；Sswell(kx,ky)是涌浪谱，采用高斯谱；ξ0是归一化参数，表示海浪高度场的二维面积。

Elfouhaily谱如式(14)：

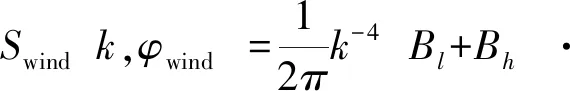
(14)

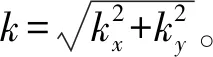
高斯谱如式(15)：

(15)

式中:σswell是涌浪的均方根高度，值为有效波高的1/4；ks_p表示高斯谱峰值点的波数，其谱宽为δk。

根据海浪高度仿真原理，只要确定4个参数：风速(Wind Speed，WS)、风向(Wind Direction，WD)、有效波高(Significant Wave Height，SWH)和涌浪方向(Swell Direction，SD)，即可实现海浪的仿真。以表1参数为例，本文实现了海浪分布仿真，仿真结果如图4(a)所示。根据机载惯导数据测量的平台高度误差和基线倾角误差，结合(10)式，实现了系统姿态误差的仿真，仿真结果如图4(b)所示。系统姿态误差和海浪分布不相关，因此将两种数据叠加,即可生成仿真高度数据(见图4(c))。

表1 海浪仿真参数

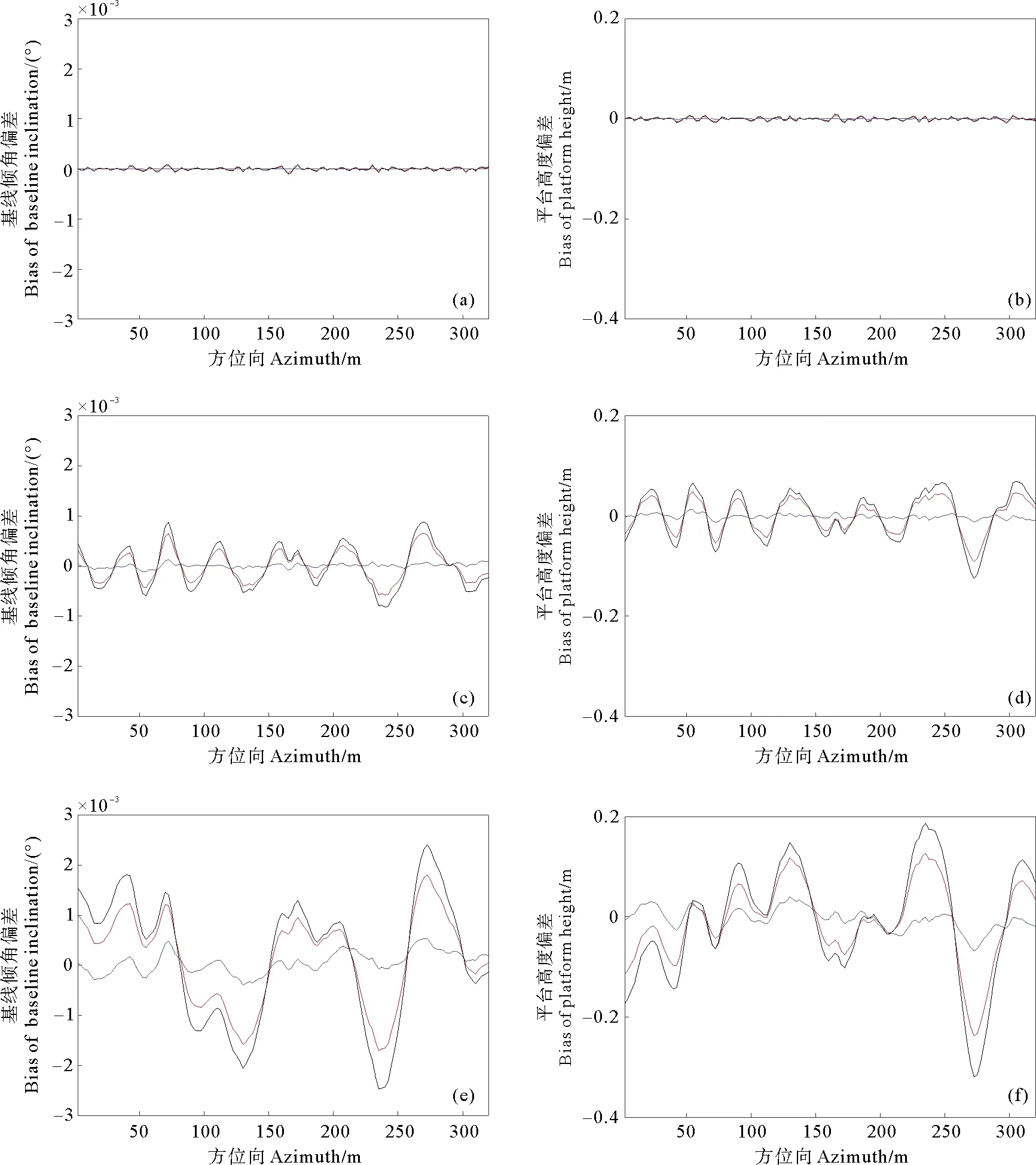
((a)、(b)、(c)分别是4、8和12 m/s风速下的基线倾角误差估计偏差；(d)、(e)(f)是4、8和12 m/s风速下的平台高度误差估计偏差。图中风向为0、π/4和π/2的误差估计偏差分别由蓝色、红色和黑色曲线表示。(a), (b) and (c) are the estimation bias of baseline inclination error under the wind speed of 4, 8 and 12 m/s respectively. (d), (e) and (f) are the estimation bias of platform height error under the wind speed of 4, 8 and 12 m/s respectively. In each image, the error estimation bias of wind direction 0, π/4 and π/2 are represented by blue, red and black curves respectively.)

2.2.2 风浪对误差估计的影响 研究风浪对误差估计的影响时，通过设置不同的风速和风向来仿真风浪分布，风速分别取4、8和12 m/s，对应低、中、高三类风速。对于每类风速，风向(与距离向夹角)分别取0、π/4、π/2，对应小、中、大风向。仿真高度数据后，分别进行误差估计，各种海况下的误差估计值和“真实值”(惯导值)的偏差如图5所示。

观察图5可知，风向和风速的增加会导致系统姿态误差估计偏差增大。当风向较小时，同一方位向的浪高随地距快速变化且分布均匀，具有很高的随机性，因此对误差估计的影响很小。随着风向的增大，同一方位向的浪高分布随机性降低，导致误差估计偏差增大，且风速越大，浪高波动越为剧烈，影响越大。

风浪的分布会影响系统姿态误差估计的准确性，从而导致估计值和“真实值”(惯导值)产生偏差。对于图5中各种风浪分布，将误差估计值和“真实值”求差，对得到的偏差进行定量计算，结果如表2所示。从表2中可以看出，相同风向下，风速的增加会导致误差估计偏差均方根显著增大。相同风速下，风向增大会导致误差估计偏差的均方根增加。这进一步证明了风速和风向的增加会导致误差估计偏差增大。表2中，风速为12 m/s，风向为π/2时，平台高度误差的均方根误差约为0.55 cm，基线倾角误差的均方根偏差约为0.000 055°，结果满足成像高度计的误差估计精度。该结果说明即使在风浪影响很大的情况下，系统姿态误差估计的精度也能满足需求。因此，在仅存风浪的海面，本文的方法能有效的实现系统姿态误差估计。

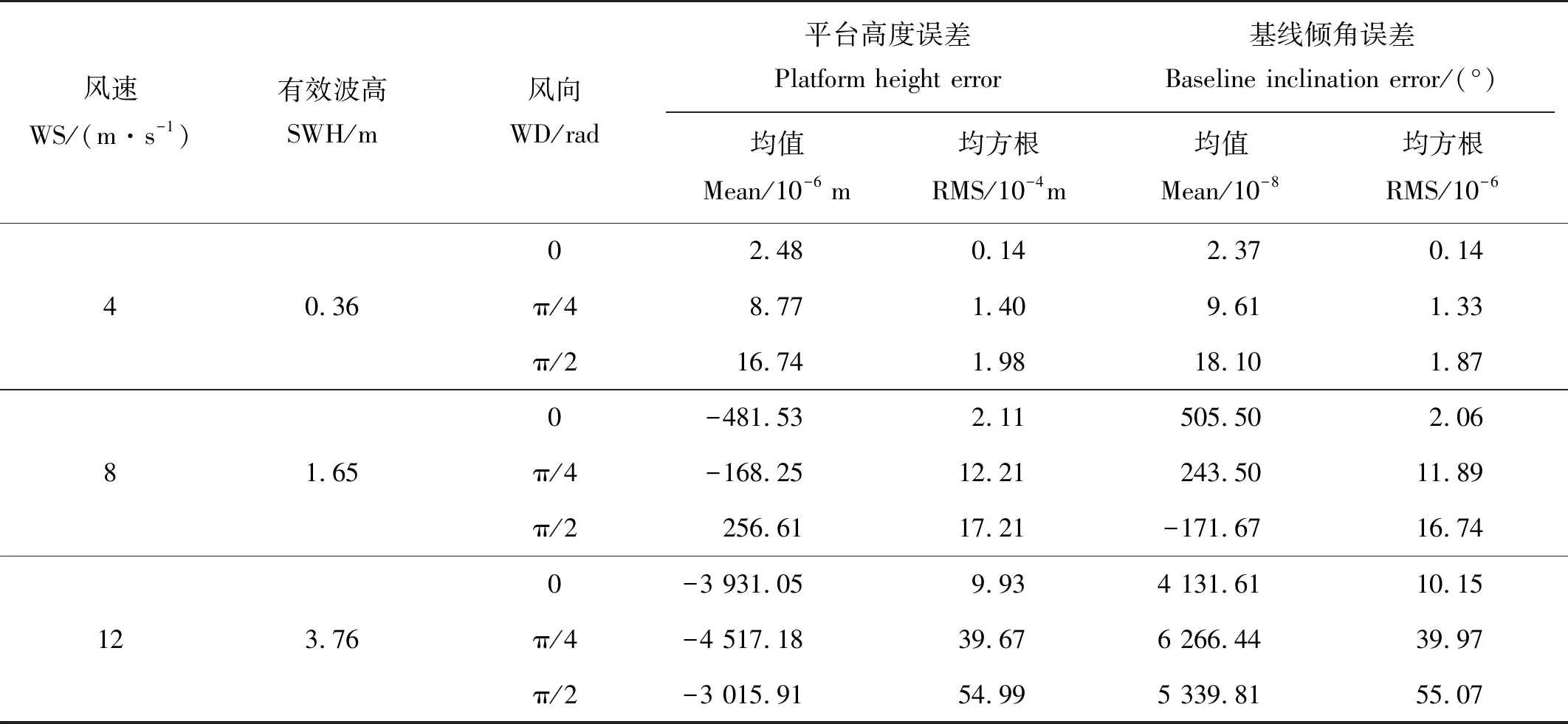
表2 不同风浪分布的估计偏差

2.2.3 涌浪对误差估计结果的影响 研究涌浪对误差估计的影响时，通过设置不同的有效波高和浪向来仿真涌浪分布，有效波高分别取1、2和4 m，对应低、中、高三种浪高。对于选定的浪高，浪向(与距离向夹角)分别取0、π/4、π/2对应小、中、大浪向。对不同海面仿真结果，分别进行误差估计，误差估计值和“真实值”(惯导值)的偏差如图6所示。

观察图6可知，涌浪方向和有效波高的增加会导致系统姿态误差估计偏差增大，这和风浪的影响一致。不同的是，涌浪的波长大于风浪，因此涌浪导致误差估计偏差的起伏频率略低于风浪。而4 m有效波高的涌浪大于12 m/s风速下的风浪的有效波高，而且涌浪的波列比风浪长，同一方位向的涌浪分布随机性更低，因此涌浪的影响比风浪的影响要大。

涌浪会影响系统姿态误差估计准确性，导致估计值和“真实值”(惯导值)产生偏差。对于图6中各种涌浪分布，将误差估计值和“真实值”求差，对得到的偏差进行定量计算，结果如表3所示。从表3中可以看出，相同浪向下，有效波高的增加会导致误差估计偏差均值和均方根显著增大。相同有效波高下，浪向增大会导致误差估计偏差的均方根增加，这也进一步反映了有效波高和浪向的增加会导致误差估计偏差增大。表3中，有效波高为4 m，浪向为π/2时，平台高度误差的均方根误差约为1.26 cm，基线倾角误差的均方根误差约为0.000 068°，满足成像高度计的误差估计精度。说明即使在涌浪影响很大的情况下，系统姿态误差估计的精度也能满足需求。因此，在仅存涌浪的海面，本文的方法也能有效的实现系统姿态误差估计。

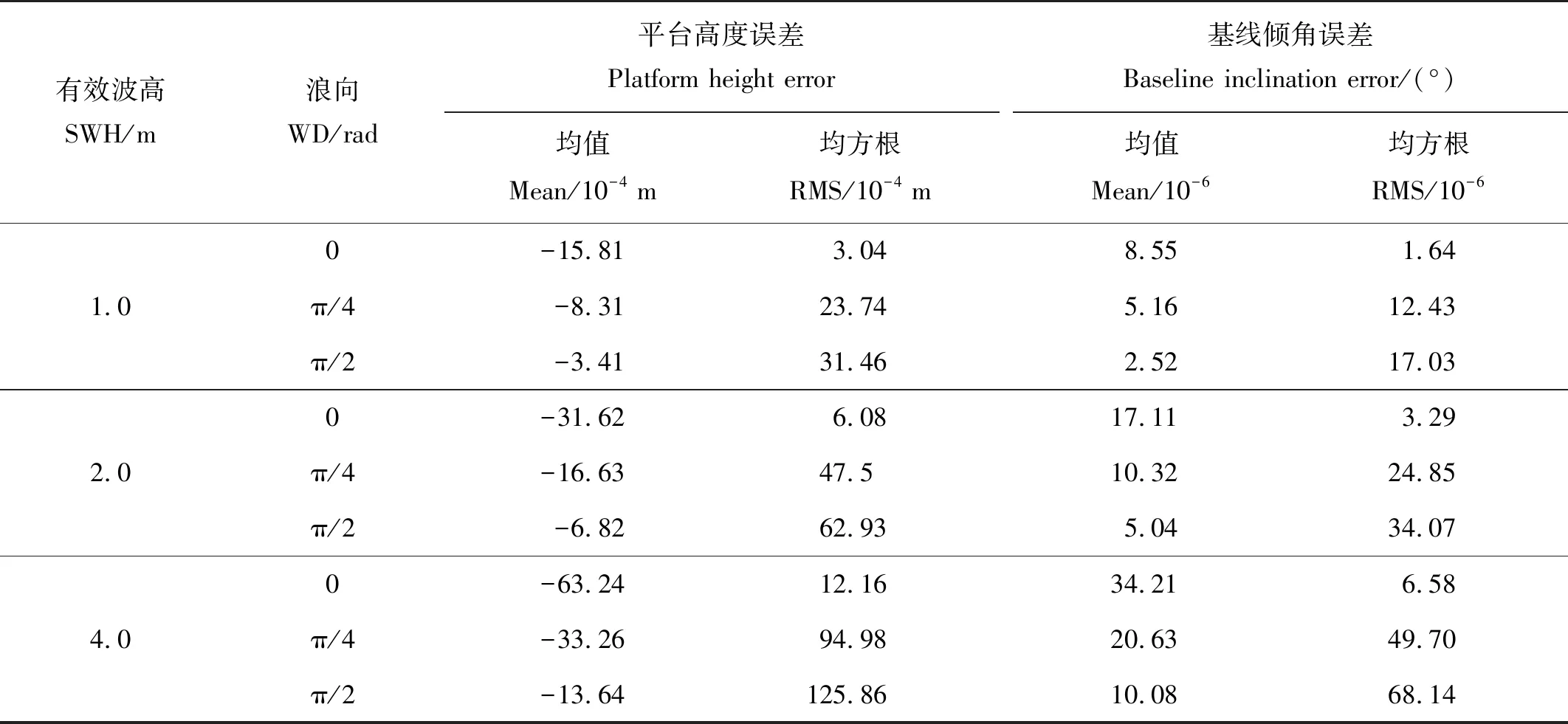
表3 不同涌浪分布的估计偏差

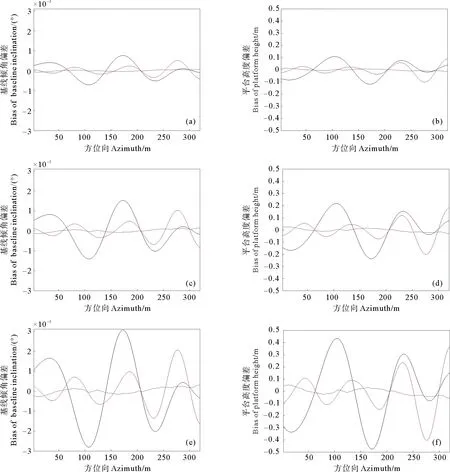
((a)、(b)、(c)分别是1、2和4 m有效波高下的基线倾角误差估计偏差；(d)、(e)(f)是1、2和4 m有效波高下的平台高度误差估计偏差。图像中,浪向为0、π/4和π/2的误差估计偏差分别由蓝色、红色和黑色曲线表示。(a), (b) and (c) are the estimation bias of baseline inclination error under significant wave height of 1, 2 and 4 m respectively. (d), (e) and (f) are the estimation bias of platform height error under significant wave height of 1, 2 and 4 m respectively. In each image, the error estimation bias of swell direction 0, π/4 and π/2 are represented by blue, red and black curves respectively.)

2.2.4 一般情况下的误差补偿 在实际测量数据中，海面既包括风浪，又包括涌浪。本文将仿真参数分为了低中高三级，表1的参数代表的是中等海况下的海浪分布。用该分布表示一般情况下的海浪分布，以该参数为例进行误差处理结果如图7所示。图7(a)是仿真的海浪分布数据，图7(b)是仿真的高度观测数据。观察图7(b)发现，系统姿态误差掩盖了海浪分布信息，且沿距离向具有明显的线性分布特征。利用本文的误差估计方法进行误差估计，并利用估计值补偿图7(b)中误差后，得到的误差补偿后的海浪分布数据(见图7(c))，其分布与图7(a)中的海浪分布几乎一致。该结果表明，本文的方法在一般情况下能有效地实现系统姿态误差补偿。

图7 仿真海浪分布(a)仿真高度数据(b)和系统姿态误差补偿后高度数据(c)

3 结语

系统姿态误差是影响成像高度计测高精度的主要误差之一，主要包括：基线倾角误差和平台高度误差。成像高度计的系统姿态误差沿距离向线性变化，根据其分布特征和最小二乘原理，本文提出了一种基于成像高度计数据的误差估计方法。该方法的精度会受到海浪分布的影响。根据海浪的分布特征，本文仿真了海表高度数据，并根据仿真数据，定性和定量分析了不同海况的影响。本文的研究结果表明，基于成像高度计数据的方法可有效地估计系统姿态误差，实现系统姿态误差补偿。需要说明的是，在10 km尺度范围内，亚中尺度海洋涡旋对海面高度异常的影响微弱，本文研究正是基于该实际情况，在忽略该尺度范围内海面高度异常的基础上开展的。对于宽刈幅成像高度计而言，亚中尺度海洋涡旋对海面高度异常的影响则不可忽略，利用本文方法开展平台姿态误差估计时，需要沿着距离向将宽刈幅图像进行分子块处理，进而开展相应系统姿态误差补偿。当然，对于该问题而言，在接下来工作中尚需进一步深入开展研究。