水平荷载作用下高桩码头整体可靠度研究❋

王浩天， 董 胜

(中国海洋大学工程学院, 山东 青岛 266100)

高桩码头作为港口码头主要的结构型式之一，由于其具有结构轻便、适应于软土地基和对水流影响小等优点而广泛使用[1]。然而，高桩码头耐久性相比重力式码头较差，起到支撑和传递荷载作用的桩基由于常年受到波浪、潮汐和船舶等动力因素，很容易发生弯曲变形、损坏以及位移等问题，存在着很大安全隐患。因此保证高桩码头的安全性是现阶段行业中急需解决的关键问题。

关于高桩码头安全性的考量可以通过码头的可靠度进行反应，但是有关可靠度的理论在高桩码头中的应用还不是很系统和完善。张戈[2]将高桩码头横向排架看作是串联系统，由此分析出高桩码头横向排架可靠度的计算方法。李声文等[3]基于ANSYS软件中概率设计模块，采用响应面法对高桩墩式码头进行可靠度分析，并对结构中可靠性指标进行敏感性分析，得到在结构中对可靠度影响较为显著的因素。以上关于高桩码头可靠度的研究中，均以构件可靠度为研究对象，然后通过体系可靠度计算方法求得整体的可靠指标，忽略了构件失效之间的联系，并不能真实反映出码头的安全性能。

王元战等[4-5]对高桩码头结构建立实体有限元数值模型，基于混凝土压碎准则进行码头承载力研究，分别得到了码头在船舶、堆货和门机荷载作用下的极限承载力所服从的分布情况。刘震宇等[6]建立高桩框架码头数值模型，将码头模型中构件的材料和几何尺寸等因素看作变量，拟合出有关堆货荷载和码头抗力的响应面方程，并结合蒙特卡罗法计算其可靠指标。这部分研究是以混凝土压碎作为判别码头失效的准则，而该准则只有基于实体建模方式才可以实现，但是实体建模较为复杂，求解不易收敛，且并不能直接得到梁板的弯矩值。同时高桩码头的失效不止局限于混凝土的压碎，还有可能是由码头位移过大，地基承载力不够等原因造成。虽然该部分的研究丰富了高桩码头可靠度研究的内容，但是求解复杂，且不能全面反映高桩码头的安全情况。

基于此，本文采用ANSYS软件建立梁板简化模型，并综合考虑码头失效模式之间的联系，进而求解码头可靠指标。既能够避免实体建模的复杂性，又能将不同的失效模式同步考虑，避免单一构件失效的片面性。同时，由于高桩码头结构主要承受来自竖向和水平向的荷载，而水平向荷载主要由船舶作用引起，数值较大，引起的码头损坏情况更为严重，且码头在竖向和水平向上的可靠度求解方法较为一致，因此本文旨在求解高桩码头在水平向的可靠度，研究结果可为码头前期设计和后期安全运营提供技术参考。

1 高桩码头模型建立

1.1 工程背景

1.1.1 地质及码头资料 以某钢筋混凝土高桩梁板码头为例进行分析[7]。该工程实例中，土层分布及物理、力学性能参数见表1。码头桩台宽度为37.5 m；桩基为650 mm×650 mm的预应力钢筋混凝土空心方桩，桩截面宽度为0.65 m，内部空心部分为圆形结构，半径为0.175 m，桩顶端为6 m的实心段；排架间距7 m；板的厚度为650 mm。码头上部面板结构采用C35混凝土，梁和桩均采用C50混凝土。其中叉桩斜率为1/3，其在水平面的投影与相应横梁的夹角为13°，码头剖面图如图1所示。

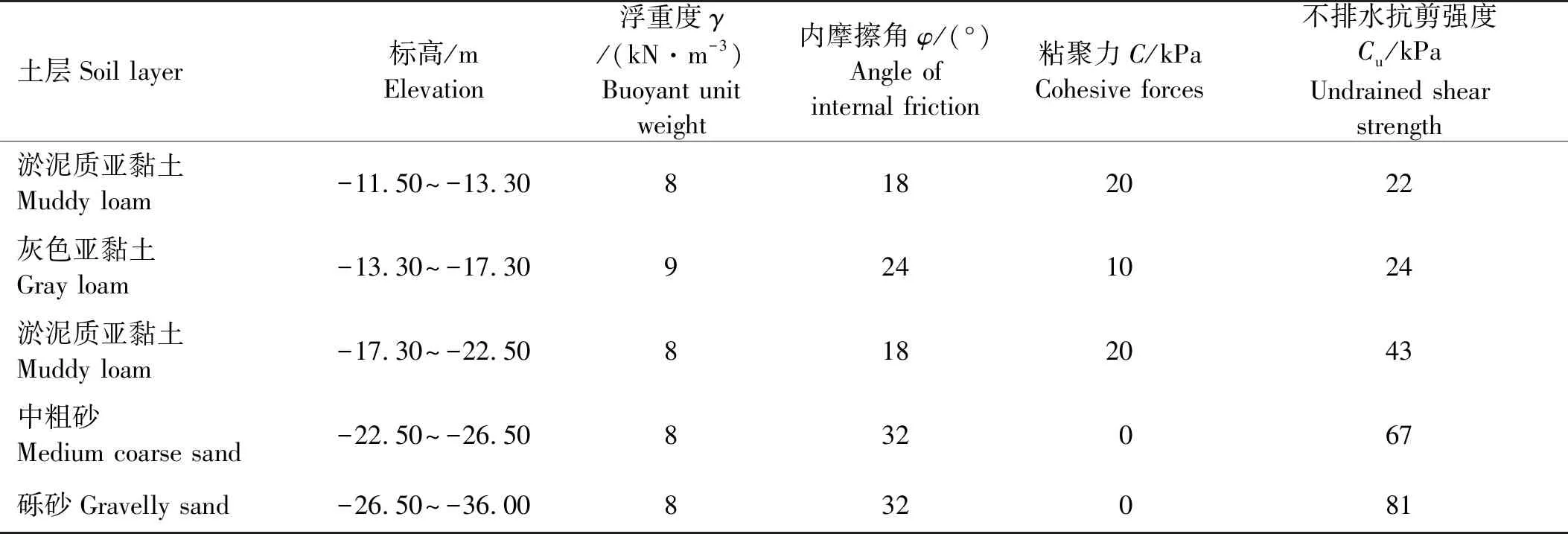
表1 土层分布及物理、力学性能参数

(标高以m计,Elevation in m)

1.1.2 码头荷载 由于本文主要分析码头结构自身在水平向上的可靠度，因此在考虑码头承受的荷载时，主要选取码头水平向的荷载，即船舶撞击力，在竖向上仅考虑码头结构自重。

1.2 桩土相互作用

高桩码头的特点之一就是可以将上部荷载通过桩基传递到土层之中，因此，对桩土相互作用的研究是分析桩基承载力乃至整个高桩码头承载力所必须考虑的问题。目前计算桩土相互作用最常用的方法是地基反力法，该方法采用Winkler地基模型，将桩周围土看作成一个个独立的弹簧，认为某一弹簧受力时仅该弹簧发生伸缩，与其他弹簧无关。虽然与实际不符，但是很多情况下该方法依然可以得到和实际较相符的桩性线，从而被广泛采用[8]。本文采用的p-y曲线法正是地基反力法中应用最为广泛的方法之一。

在采用软件模拟过程中，先根据提供的地质资料绘制出桩土的侧向荷载-位移传递曲线，即p-y曲线、轴向荷载-位移传递曲线，即t-z曲线、桩端荷载-位移传递曲线，即q-z曲线。在ANSYS中通过COMBIN39弹簧单元模拟桩土的非线性作用，表征弹簧性能的参数则需要通过单元实常数赋予，所以需要将这些曲线离散成所需的实常数[9]。在建立弹簧单元时，在桩侧两个互相垂直的方向上(X和Y方向)建立垂直于桩轴线的切向弹簧单元，并按照p-y曲线赋予单元实常数，以模拟侧向抗力；在桩的轴向上(Z向)沿着桩身建立竖向弹簧单元，并按照t-z曲线赋予单元实常数，以模拟桩侧摩阻力；在桩顶建立桩端法向弹簧单元，并按照q-z曲线赋予单元实常数，以模拟桩端阻力。弹簧单元的具体布置如图2所示。其中有关p-y曲线、t-z曲线和q-z曲线的计算及绘制方法详见文献[10]。

图2 弹簧单元布置图

1.3 单元选取及模型建立

根据文献[11]的建议，本文采用空间梁板简化模型。在模型单元选取时，考虑到梁板之间的空间相对位置，码头面板采用可以考虑截面偏移的SHELL181单元。单元厚度和其他参数可以通过实常数或者壳截面进行定义，该单元模拟薄壳至中等厚度的壳结构具有很好的适用性[12]。码头纵、横梁以及桩采用适合模拟梁结构的BEAM188单元。对于纵、横梁和桩顶实心段的截面，直接通过SECTYPE命令调取矩形(RECT)截面，并通过SECOFFSET命令设置截面偏移和SECDATA命令设置截面尺寸；对于桩的空心段截面，需要通过SECWRITE和SECREAD命令自定义截面。划分网格时，面板和纵横梁以50 cm为一个单元，桩基每1 m划分一个单元。码头数值模型如图3所示。

图3 码头数值模型

2 码头水平向可靠度计算

2.1 随机变量的确定

求解可靠度前，需要获得结构的抗力和荷载效应的概率分布及其参数，采用极限状态方程Z=R-S=0进行求解。本文算例的S按1.1.2节选取。确定船舶撞击力方法为：根据设计船型及其撞击速度计算船舶撞击能量，选取相应的橡胶护舷，护舷的反力即为船舶撞击力。算例的设计船型为5万吨级集装箱船，护舷为圆筒型φ1 600×φ800橡胶护舷[13]，吸收能量为276.4 kJ，计算所得的船舶撞击力为780 kN。对于码头抗力，考虑材料性能和构件几何参数对结构抗力的影响。通过查阅文献[14-15]，列出本文考虑的随机变量的种类及其概率分布类型和统计参数，如表2所示。

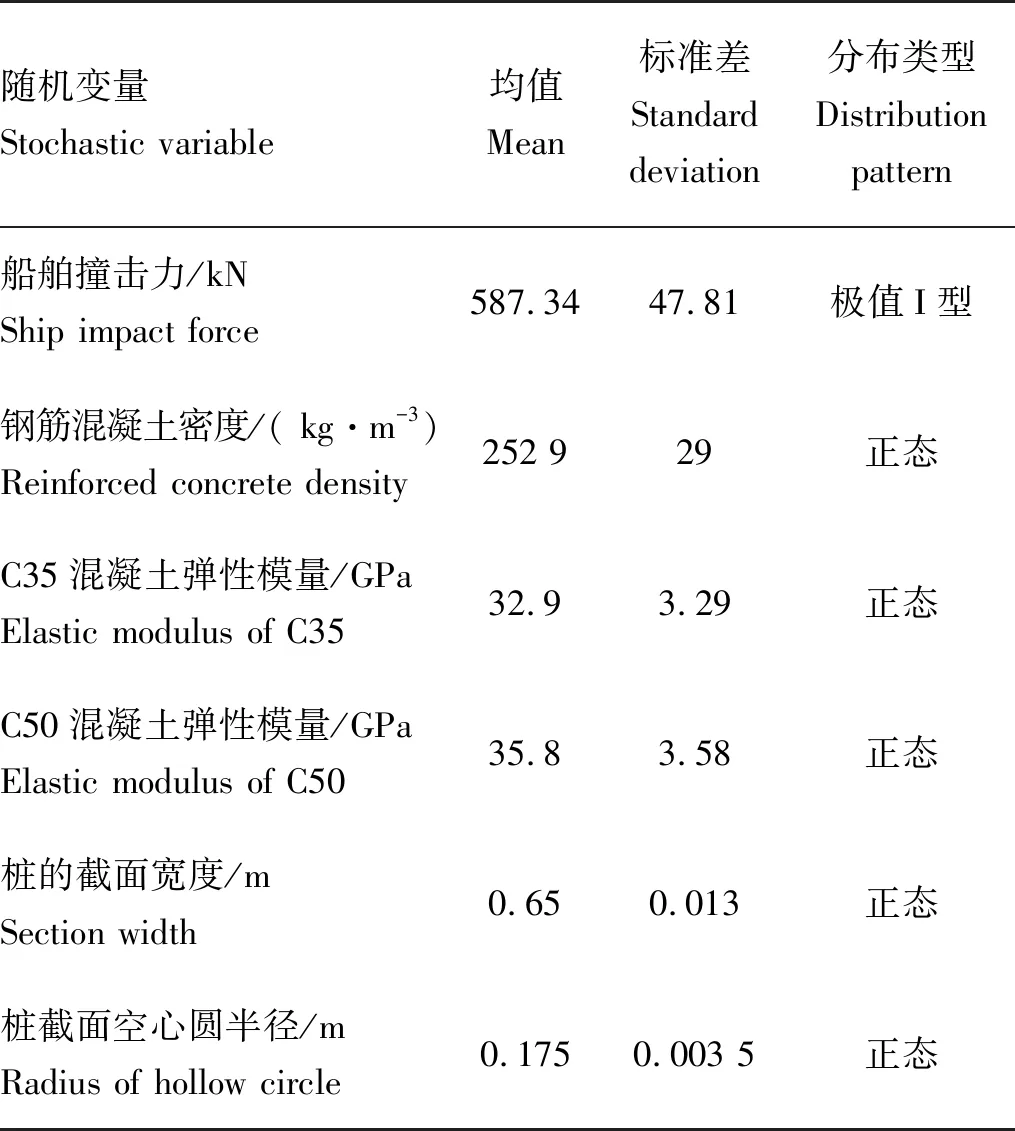
表2 随机变量分布类型及统计参数

2.2 失效模式的确定

高桩码头作为复杂的大型结构物，其失效模式众多，鉴于考虑所有的失效模式过于复杂且难以实现。本文选取梁板式高桩码头中受水平荷载作用下较为常见的两种失效模式作为码头失效的判别标准，即码头面板位移失效模式和码头桩基强度失效模式。

2.2.1 码头面板位移失效模式 由于高桩码头承受船舶撞击力，会导致码头发生水平向位移，挤压面板的同时也会导致桩基受力的变化，影响码头安全，故码头面板位移的过大会导致码头失效。面板位移的极限值可根据规范ACI 318M-05确定，其数值为支承构件长度的1/180[16]。支承构件长度在高桩码头中为桩的受弯计算长度，即桩顶到假想嵌固点的距离。具体计算如下[17]：

桩的换算宽度可由下式计算：

当d≥1.0 m时，b0=kf(d+1)≤2d。

(1)

当d<1.0 m时，b0=kf(1.5d+0.5)≤2d。

(2)

式中：d为桩宽(m)；kf为形状换算系数。

桩的相对刚度特征值可由下式计算：

(3)

式中：EP为材料弹性模量(kN/m2)；IP为截面惯性矩(m4)；m为系数，可根据地质资料查规范JTS 167-2018中表B.3.1取值[17]。

桩顶至假想嵌固点的距离，按下式计算：

L=l+t。

(4)

式中：l为桩顶至泥面距离(m)；t为嵌固点至泥面距离(m)，t=ηT，其中η为系数。

由此可以计算出当输入的参数均为各个变量的均值时，码头面板位移失效模式的极限值为9.745 8 cm。由于在本文中，输入参数是通过拉丁超立方(LHS)抽样得到的随机变量，因此计算得到的码头面板位移失效模式的极限值也是变量，针对每一组不同的输入变量对应着不同的面板位移极限值，当由荷载引起的码头面板位移值大于对应的极限值时，码头处于面板位移失效模式。

2.2.2 码头桩基强度失效模式 考虑到在高桩码头中，桩基不仅作为码头的支撑结构，同时还可以将上部结构承受的荷载传入到地基之中，因此桩基结构的强度问题至关重要。码头桩基强度失效模式的极限状态为桩基混凝土的应力达到其抗压强度，即当码头承受荷载时，桩基的等效应力大于桩基混凝土的抗压强度时，码头处于桩基强度失效模式。本文中，桩基采用C50混凝土，其抗压强度的标准值为32.0 MPa[18]。由于混凝土的抗压强度作为检验该模式是否失效的标准，且是抗力的组成因素，应具有相应的统计参数。结合文献[15]中表5-7知，桩基混凝土抗压强度的平均值为36.16 MPa，变异系数为0.10。文献[14]编制组通过对港工混凝土强度的概率分布类型进行假设检验得知，港工混凝土强度更多的服从于正态和对数正态分布，且很难区分，但从工程应用角度，本文选用正态分布作为港口工程混凝土的概率分布类型。

2.3 水平向整体可靠度分析

2.3.1 水平向极限承载力提取 码头在承受船舶撞击力作用下会发生水平位移，同时导致桩基弯曲产生弯矩，致使桩基的应力增加，码头会发生面板位移失效和桩基强度失效这两种失效模式中的任意一种失效，且每一种失效模式都有对应的极限值，该极限值对应的船舶撞击力便称为码头在该失效模式下的水平向极限承载力，取两个极限承载力中的较小值，便为码头水平向极限承载力，如图4所示。

图4 水平向极限承载力判别标准

ANSYS中提取水平向极限承载力样本的过程如下：

(1)将表2中除船舶撞击力之外的其他随机变量进行蒙特卡罗抽样，抽样次数为500次，得到500组变量样本。

(2)提取一组变量，根据2.2节内容，计算面板位移失效模式的极限值；并将均值为36.16 MPa，变异系数为0.10且服从正态分布的桩基混凝土抗压强度进行LHS抽样，得到桩基强度失效模式的极限值。

(3)将提取出的这一组变量值赋予模型中对应的参数，并建立相应的数值模型。

(4)在模型上以荷载步的形式逐级加载船舶撞击力，通过软件后处理提取每一荷载步作用下的面板最大位移值和桩基最大应力值，并储存在建立的TABLE中。在TABLE中通过插值的方法分别提取出由步骤(2)计算得到的面板位移极限值和桩基应力极限值所对应的船舶撞击力，取较小的船舶撞击力作为该组数据下的码头水平向极限承载力。

(5)重复步骤(2)～(4)共计500次，得到500个码头水平向极限承载力样本值。

2.3.2 水平向极限承载力样本分布拟合 将得到的码头水平向极限承载力样本除以水平向极限承载力标准值后，再进行分布拟合。其中，标准值为当模型中的输入参数均为其对应的均值时所提取得到的水平向极限承载力。除以标准值的这一步操作称之为去量纲化，可以使数值计算更为方便，便于数学处理。表3为水平向极限承载力样本统计参数。

表3 水平向极限承载力样本统计参数

根据文献[14]中对有关港口码头荷载和抗力参数的统计分析知，在港口工程中，以正态分布、对数正态分布和极值I型分布出现的频率最高。因此本文采用MATLAB软件中“Distribution Fitting”功能对得到的水平向极限承载力样本进行以上三种分布的拟合。

图5、6分别为水平向极限承载力样本分布概率图和样本值概率密度分布的拟合图。二者均表明，样本值集中的分布在正态分布和对数正态分布的线上，样本数据两端较多的偏离极值I型分布，由此可知该样本更近似于服从正态分布或对数正态分布。

图5 水平向极限承载力样本分布概率图

2.3.3 水平向极限承载力样本假设检验 以上通过对水平向极限承载力样本分布的拟合，只得到该样本近似服从正态或对数正态分布，至于具体服从哪一种分布还需要进行假设检验。假设检验的原理是先对需要检验的样本分布进行某种形式的假设，再根据样本构造出合适的统计量，进而对提出的假设做出检验，并判断是否接受或者拒绝原假设。假设检验实质上是一种反证法，如果要检验某一假设H，先假设H正确，并基于此构造事件A，但要求事件A在H正确的前提下发生概率很小，然后进行一次试验，如果A发生了，则与小概率事件原理相矛盾，即之前的假设是错的，因而拒绝H；反之，便不能拒绝H，通常接受H[19]。对样本进行检验的方法有很多，各有适应范围和优缺点，本文基于MATLAB软件采用卡方拟合优度检验、Jarque-Bera检验、Kolmogorov-Smirnov检验、Lilliefors检验和Anderson-Darling检验，共计五种检验方法对上述得到的码头水平向极限承载力样本进行分布假设检验，得到检验的p值，汇总结果见表4。

图6 水平向极限承载力样本值概率密度分布的拟合

表4 水平向极限承载力样本假设检验p值结果

在本次假设检验中显著性水平取0.05，若返回的检验p值小于等于0.05，则拒绝预先做出的假设，否则接受该假设。从表中可以看出正态分布返回的检验p值均大于0.05，但是对数正态分布中只有卡方拟合优度检验、Kolmogorov-Smirnov检验和Lilliefors检验返回的p值大于0.05，其余2种检验均小于0.05。所以本次检验认为水平向极限承载力样本服从正态分布。需要说明的是，码头水平向极限承载力主要取决于影响码头抗力的因素，而每个码头中影响抗力的因素不一致，故所得的承载力分布也不是统一的，但是本文所介绍的求解码头水平向极限承载力服从分布的方法，对工程实际有参照意义。

2.3.4 水平向整体可靠度计算 结合极限状态方程Z=R-S=0，可以将码头承受的水平向荷载，即船舶撞击力等效为S，是均值为587.34 kN，标准差为47.81的极值I型变量；将码头水平向极限承载力等效为R，是标准值为23 905.878 2 kN，均值和标准值比值为0.989 2，变异系数为0.047 3的正态变量。两者的具体分布和统计参数均已得知，进而可以求解其可靠度。

本文利用MATLAB软件，采用JC法编写求解可靠度的程序，通过计算得出码头水平向整体可靠指标为21.78。该可靠指标的数值较大，表明本文选取的工程结构较为安全，其自身结构安全储备较大；同时也表明，该码头设计船型的选取较为保守，可适当增大设计船型的吨位。

3 结论

高桩码头作为港口装卸作业的载体，其安全性至关重要。本文基于ANSYS软件，以某工程为实例，提出一种通过考虑失效模式之间的联系进而求解高桩码头可靠指标的方法，得到以下结论：

(1)通过提取码头水平向极限承载力并进行样本分布的拟合和假设检验，得知本工程实例中的码头水平向极限承载力样本服从正态分布。这对于分析码头水平向的安全性提供便捷和依据。

(2)采用JC法计算本工程实例中的码头水平向可靠指标为21.78。由此说明该码头自身结构在水平向的安全储备较大，对码头安全运营提供了参考。

实际工程中，高桩码头的失效模式有多种，如码头面板位移失效模式、码头桩基强度失效模式、土壤极限承载力失效模式、以及桩基极限变形失效模式等。根据工程经验，水平荷载作用下，前两种失效模式为控制工况，为了简化计算，本文仅考虑了前两种失效模式。然而，要获得水平荷载作用下更为全面的高桩码头结构可靠度，应综合考虑多种失效模式。