基于Argo温度异常剖面的海洋涡旋无监督分类方法研究❋

林 静， 马纯永，2❋❋， 陈 戈，2

(1. 中国海洋大学信息科学与工程学院， 山东 青岛 266100； 2. 青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室， 山东 青岛 266237)

中尺度涡旋在世界各大洋中广泛存在，通常分为气旋型涡旋(Cyclonic eddies, CEs)和反气旋型涡旋(Anticyclonic eddies, AEs)，中尺度涡旋裹挟的水团存在温盐异常，并能保持所携带水体的特性，对全球海洋的水体、能量和物质输运都发挥着重要作用[1]。根据不同的研究目标，科学家们开始逐渐研究具体类型的涡旋。有多种涡旋分类方法，其中最常用的一种是仅根据区域范围对涡旋进行分类，例如黑潮延伸体区域的涡旋[2]、南太平洋东部的涡旋[3]、印度洋东南部的涡旋[4]及南海涡旋[5]等。在这些地区，海洋科学家们分别研究涡旋的气候特征。同时，还有一些针对特定类型涡旋的研究，其主要是基于对涡旋某些特性(半径、振幅、传播轨迹、寿命等)的分类。例如，Chen等[6]根据寿命的不同对涡旋进行分类，并发现短寿命和长寿命涡旋的分布是具有空间聚集效应且在空间上相互分离。但上述分类方法难以对垂直结构相似的涡旋进行自动分类，从而不能揭示特定类型涡旋的动力机制。因此，基于海面下Argo浮标剖面的涡旋分类方法有待进一步研究。

Argo (Array for Real-Time Geostrophic Oceanograph) 浮标计划是一个实时全球海洋观测网络，由大约4 000个随机分布在各大洋的自动剖面仪组成，旨在快速、准确、大范围地收集海洋上层的海水温盐剖面资料。全球Argo阵列的实现，可获得快速、准确、大尺度的温盐剖面[7]，这使得全球中尺度涡旋垂直结构的研究成为可能[8-10]。随着卫星高度计的发展和现场数据的不断积累，海洋大数据挖掘技术成为海洋科学研究的焦点。近年来，Argo温度/盐度剖面聚类技术已用于若干海洋应用研究中。Pegliasco等[11]为确定研究区域海表和次表层异常涡旋的比例，对涡旋内的Argo剖面进行聚类分析，并根据温盐异常描述涡旋的垂直结构。Maze等[12]利用高斯混合建模的无监督聚类方法(Gaussian Mixture Model，GMM)对北大西洋Argo温度剖面数据进行分类。其结果表明，即使在不使用空间信息的情况下，相同类别剖面在空间上具有一致性。然而，Maze指出当数据集量较大(超过7 000)时，GMM方法并不令人满意，需要通过限制数据集的大小来计算类的数量。为了突破大数据分类的局限，本文提出了一种改进的GMM方法，该方法可客观计算数万条Argo剖面的类数，在不输入任何空间信息的情况下，有效地实现Argo温度异常剖面的聚类。本文实验区域为28°N—40°N, 140°E—180°E，此区域被称为黑潮延伸体(Kuroshio Extension, KE)。KE区域作为北太平洋的两个强涡旋动能带之一[13-14]，黑潮蜿蜒的形成与此区域涡旋的活动密切相关[15-16]。许多研究人员指出，该区域生成的涡旋在空间上并不统一，这与每个子区域的独特动力机制和水团起源相关，它们有可能起源于KE区域、亲潮、津落暖流和鄂霍次克海[14,17-18]。Dong等[19]为研究涡旋结构的空间变化，将KE区域划分为9个网格并比较了这9个网格中的合成涡旋。但具有不同垂直结构的涡流将共存于同一个网格中，从而无法进一步区分。本文研究的主要目的是通过对Argo温度异常剖面数据进行聚类，进而实现与其时空匹配涡旋的分类。

1 数据

1.1 涡旋识别数据

本文采用的是1998—2018年的日网格化海平面异常(Sea Level Anomaly, SLA)数据。SLA数据是由法国海洋卫星数据处理中心存储、验证、解释(AVISO；http://www.aviso.oceanobs.com)，其空间分辨率为(1/4)° × (1/4)°。KE地区中尺度涡旋的识别是基于Liu等[20]的工作，涡旋识别数据集发布在http://coadc.ouc.edu.cn/tfl/上。本文采用的KE区域涡旋数据集包含12 171个AEs和12 672个CEs。不同数值大小的涡旋半径和振幅的数目分布如图1所示。半径和振幅是涡旋的两个重要参数。涡旋半径的直方图显示，反气旋和气旋的分布相似，且在40 km左右都有峰值。其峰值半径与黑潮的水平剪切尺度或第一斜压变形半径的阶数相同[21]，这意味着涡旋的产生可能是由于剪切不稳定或斜压不稳定。

1.2 Argo剖面和CARS气候态数据

本文采用的Argo剖面数据是法国科里奥利全球数据采集中心提供的1998—2018年的延迟模式数据(http://www.coriolis.eu.org)。KE区域存在大量Argo剖面[22]，这为本次实验提供了充足的数据，为研究的顺利开展奠定了基础。

Argo数据经过数据中心的自动质量控制和分析程序，本文仅使用质量标记为1或2(表示“良好”或“可能良好”的质量)且为延迟模式的Argo剖面数据。为保证数据精度，我们使用与Chaigneau等[23]类似的质量控制条件，剖面数据需要满足以下标准:

(1)每个剖面最浅的海表数据的深度在0～10 dbar之间，最深采样深度深于1 200 dbar。

(2)每个剖面连续两个数据点的采样深度间隔不得超过以下范围:

(a)0～100 dbar之间的数据间隔不得超过25 dbar;

(b)100～300 dbar之间的数据间隔不得超过50 dbar;

(c)300～1 000 dbar之间的数据间隔不能超过100 dbar。

(3)每个Argo剖面数据在1 000 dbar以上至少有30个有效点。

基于上述标准以及与涡旋的时空匹配，研究区域的涡旋内总共有24 608个剖面，其中有12 873(11 735)个剖面在AEs(CEs)内。该数据集中所有剖面的位置分布如图2所示。研究区域的西边Argo剖面分布密集，东部分布较为稀疏。为了获得合成涡旋的温盐结构，本文用涡旋内部Argo温盐剖面数据减去气候态温盐剖面数据得到涡旋内部温盐异常。本文采用的气候态温盐剖面数据来自名为CSIRO Atlas of Regional Sea 2009(CARS09)的数据集[24-25]，其在全球海洋空间分辨率为0.5(°)×0.5(°)。CARS09气候态数据在深度分布上共有79层，深度可达水下5 500 m。且CARS09文件包含的主要参数除了格点的经纬度以及标准层对应的深度等信息外，还包括平均数，年循环的正弦值，年循环的余弦值等必要数据。利用这些数据可得到一年之中任意一天某一深度上的温度以及盐度数据，数据可靠度较高。

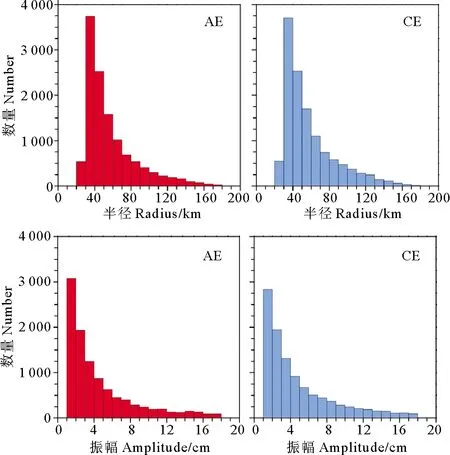
(AE:气旋型涡旋 Cyclonic eddies; CE:反气旋型涡旋 Anticyclonic eddies)

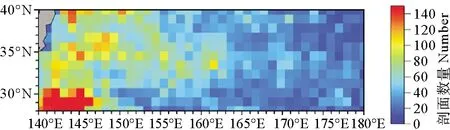
图2 1998—2018年KE地区 每个(1)°×(1)°格子里涡旋内剖面数量Fig. 2 The number of profiles surfaced inside eddies in 1(°)×1(°) from 1998 to 2018 in KE region

2 方法

2.1 高斯混合模型

本文采用的无监督聚类方法称为高斯混合模型(GMM)，该方法通过多个高斯分量的线性组合来估计数据集的概率密度函数(Probability Density Function，PDF)，每个高斯分量代表一个类。高斯混合模型可表示为PDF的加权和[26]。

(1)

该模型共由k个混合成分组成，每个混合组成对应一个高斯分布。其中：μk是n维均值向量；∑k是n×n的协方差矩阵，它们对应着第个高斯混合成分的参数；N(X；μk，∑k)是概率分布密度，而λk≥0为相应的“混合系数”，∑λk=1。本文将描述混合高斯模型的三个参数记为θk，即混合系数λk，均值μk，协方差矩阵∑k。因此，高斯混合模型由参数集θk确定。本文使用期望最大化算法来确定θk，其通过迭代的方式从含有隐含变量的完整数据中求解极大似然估计的参数。

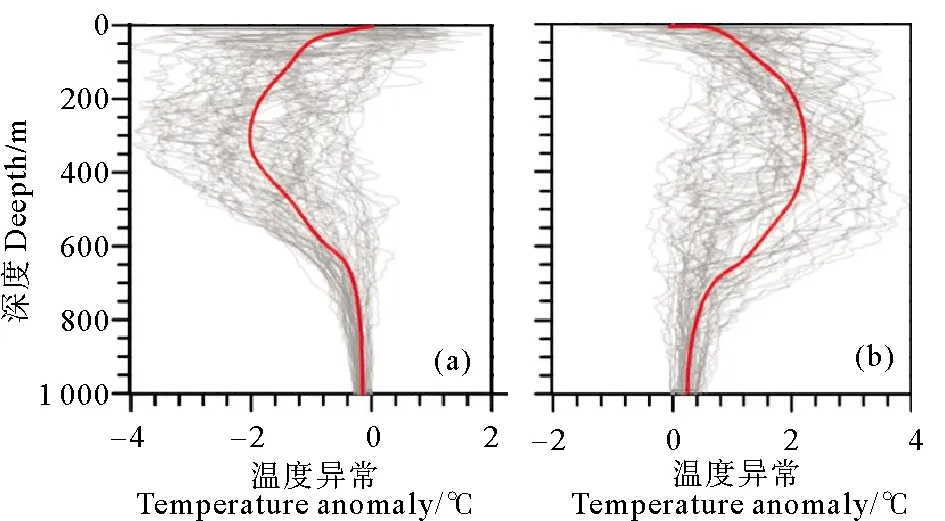
((a) 30个剖面位于CEs内部，(b) 30个剖面位于AEs内部。红色曲线为平均异常剖面。30 profiles are inside the cyclone eddies (a) and 30 profiles are inside the anticyclone eddies (b).The red curves are the average anomaly profile.)

本文目标是将KE区域涡旋内部Argo温度异常剖面进行分组。如图3所示，它们是从Argo温度异常数据集中随机选取60个剖面绘制的，这60个剖面的最大温度异常值所处深度和绝对值大小是变化的。GMM可对数据集中温度异常剖面的多样性统计地表示，PDF可捕获剖面沿垂直轴采取给定模式的相对可能性。GMM可将Argo温度异常曲线的PDF分解为多维高斯PDF的加权总和，并且每个压力水平都被视为“维度”[27]。如果模式在集合中是经常出现的，则其实例将累积并在PDF中创建一个峰值。同样，如果重复出现多个模式，则将观察到带有多个峰的PDF。因此，基于GMM的聚类方法可用于分析垂直温度异常剖面的多样性，并聚类出相似剖面的组。

2.2 优化的GMM的两个关键点

首先，在GMM模型中提出了一种新的混合成分值选择方法，该方法可以直接计算大量剖面的分类数。其次，根据不同聚类结果之间的空间相邻关系和平均剖面特征的相似性，将聚类结果进行合并，得到可用于KE区域合成旋涡分析的最终聚类结果。

GMM只有一个自由参数混合成分，即类的数量。许多参数估计问题采用似然函数作为目标函数。当训练数据足够时，模型准确率可不断提高，但以增加模型复杂度为代价，也带来了机器学习中常见的问题，那就是过拟合。为了避免模型的过拟合，人们提出了许多信息准则来增加模型复杂度的惩罚项。为了确定的最合适值，Maze等[12]使用贝叶斯信息准则(BIC)进行模型选择，计算方法为：

BIC=-2 ln(L)+kln(n)。

(2)

式中：L为似然函数；k为模型参数个数；n为样本数量；kln(n)是惩罚项。在维数过大且训练子集相对较少的情况下，惩罚项可有效地避免维度灾难现象。但这种方法在应用于剖面数据集时并不令人满意，因为数据集大意味着对数似然值远大于惩罚项，这使得这种模型选择方法无效。

为避免上述问题,我们在二维空间上(横轴为温度异常，纵轴为深度)计算聚类子集的聚合程度(ADk)，以此来判断无监督聚类后的剖面子集类的合理性。ADk可用下面的公式计算。

(3)

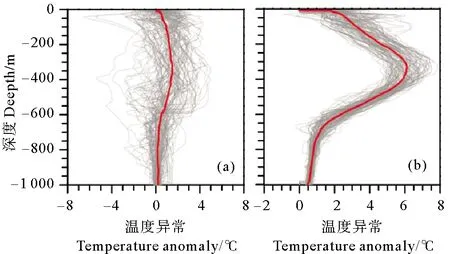
(红色曲线为平均异常剖面。The red curves are the average anomaly profile.)

本文在GMM的基础上，针对合成分析的要求，提出了一种新的混合成分值判定方法，利用每一类剖面子集在不同维度上的方差以及每一类所占的权重来计算不同值对应的Score，如图5所示，Score值越小代表模型越好。计算Score公式如下：

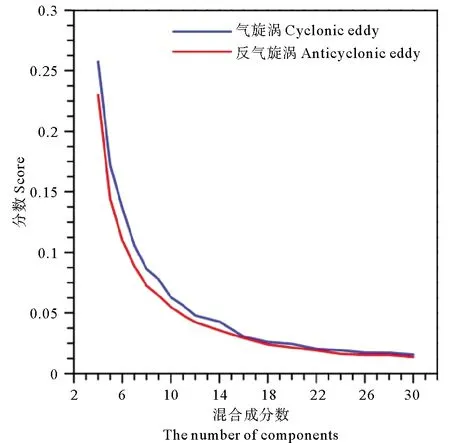
图5 混合成分的数目和的对应数值关系Fig.5 The relationship between k and Scorek

(4)

当k=24时，Scorek到达一个相对较小的值,当k继续增长，Scorek没有明显变化。因此,本文训练GMM的聚类结果为24类。这种确定值的新方法在处理

大量剖面时也能有效地避免维度灾难。

另一个改进是合并聚类结果的步骤。此步骤对于合成分析至关重要。合并之前，绘制了当前24类GMM聚类结果剖面(GMM clustering results, GCRs)的空间分布。发现了两个有趣的模式：首先，24类剖面在空间上具有聚合效应。其次，最大异常较浅的剖面类主要分布在KE的北部，中层的异常主要分布在KE流轴附近，而深层的异常则分布在KE的南部。根据这些模式，本文客观地定义了以下合并规则：平均温度异常剖面的最大异常绝对值所处深度为300 m以浅的剖面类别被分类为表层异常，平均最大温度异常绝对值在300～450 m的剖面类别被分类为中层异常，平均最大温度异常的绝对值在450～600 m处的剖面类别为深层异常。

2.3 算法过程

本文选择Argo温度异常剖面的部分子集对GMM进行训练，然后使用训练过的模型对所有Argo温度异常剖面进行聚类。本文通过在整个集合中随机选择剖面来创建一个训练子集。这个训练子集主要根据Argo剖面在黑潮延伸体区域的分布密度来选取，保证每个1(°)×1(°)的格子都有剖面被取到且选取数量为每个格子剖面数量的75%。最终，训练子集的AEs(CEs)内剖面数量为9 650(8 800)条。上文已对优化的高斯混合模型聚类算法涉及元素做了充分介绍，下面是总结了运用优化的GMM对Argo温度异常剖面进行无监督分类的过程：

Algorithm: Argo profiles clustering based on GMMInput:X={x1,x2,…,xn} , classesmax of GMM K;Output: the optimum number of classes k , GMM model;begin:1. create a training subset X=X={x1,x2,…,xn} ;2. set of classesmax GMM K;3. for k from 1 to K {4. train a GMM model: computer the best set θ={λk,μk,∑k,k=1…k} with the EM algorithm;5. compute scorek using the guidance from 3.2;6. if () {scorek+1≈scorek){ score∗=scorek+1} else {7. return to step 4; }8. until scorek+i+1≈scorek+i;9. continue}end

通过该算法可以得到最佳分类数和最佳参数θ*={λk,μk,∑k}。在此基础上，根据上一节中表述的规则合并GCR。如果某些剖面类符合上述条件，但它们的平均剖面特征(例如具有双核垂直结构的GCR)与其他类型有很大差异，则这些剖面类将不会合并到合成分析的数据集中。

3 结果与分析

3.1 聚类结果

本文将AEs内Argo温度异常剖面的GCRs按照异常深度从浅到深来介绍(见图6)。图6(a),(b)是AEs内Argo剖面温度异常最大值所处深度在300 m以浅的7类剖面类，图6(c),(d)是温度异常最大值在300～450 m之间的7类温度异常剖面类，图6(e),(f)是温度异常最大值在450～600 m之间的7类温度异常剖面。图6左部(a),(c),(e)对应的是相应异常深度的强异常的剖面类，右部(b),(d),(f)对应的是弱异常的剖面类。通过每一幅图横轴的数值来看，在300～450 m处的最大温度异常值异常程度最大。

((a)～(f)按照温度异常最大值所在深度由浅入深的顺序展示。(a)～(f) are shown in the order from shallow to deep in the depth of the maximum temperature anomaly.)图6 反气旋涡内Argo温度异常剖面聚类后的结果Fig.6 Clustering results of Argo temperature anomaly profiles inside AEs

同样，图7(a),(b)为CEs内Argo剖面温度异常最大深度在300 m以浅的7类剖面;图7(c),(d)为温度异常最大深度在300～450 m之间8类剖面;图7(e)和(f)为温度异常最大深度在450～600 m之间的7类剖面。从各图横轴上的值可以看出，在300～450 m处的最大温度异常值异常程度最大。

需要解释的是，AEs(CEs)内Argo温度异常剖面聚类结果有24种，图6(7)中有21(22)类结果。图8(a),(b)分别为AEs和CEs内剖面聚类结果未显示的类别，从图中可以看出，舍弃的剖面类主要由于暖涡(冷涡)中存在冷(暖)信号，这种类型会对合成涡旋的一般结构产生干扰，因此舍弃。

(图(a)～ (f)按照温度异常最大值所在深度由浅入深的顺序展示。(a)～(f) are shown in the order from shallow to deep in the depth of the maximum temperature anomaly.)

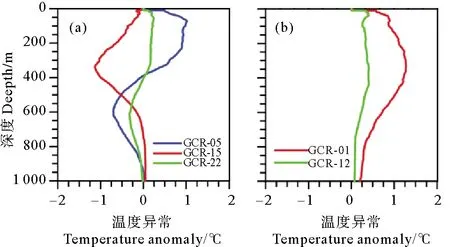
图8 反气旋涡内舍弃的3类平均温度异常垂直剖面(a)及 气旋涡内舍弃的2类平均温度异常垂直剖面(b)Fig.8 Vertical profile of the three types of average temperature anomalies discarded inside the AEs (a) and vertical profile of the two types of average temperature anomalies discarded inside the CEs (b)

3.2 中尺度涡旋合成分析结果

根据KE区域涡旋内Argo温度异常剖面的聚类结果，作者按照2.2合并聚类结果的步骤，将图6,7中剖面类别进行合并。图9显示了KE区域浅层、中层、深层异常三种类型的合成CE(蓝线)和AE(红线)的平均温度异常(T′)、盐度异常(S′)及其剖面分布密度图。从图9(a),(c),(e)三种合成CE(蓝线)和AE(红线)的中可以看出，在垂直方向上分布有两个相同的特征。首先，随着海平面深度的增加而增加，之后随深度的增加而减少；其次，三幅图中异常主要局限在800 m以上，1 000 m处的温度异常幅度都减小到小于0.5。另外，还有两个点需要注意，在图9(a),(c),(e)中，的最大异常深度是分别递增的，合成CE与AE分别在193 m(226 m)、379 m(364 m)、540 m(519 m)处达到最大值，且最大值分别为-2.4 ℃(2.5 ℃)、-3.5 ℃(3.7 ℃)、-1.5 ℃(1.8 ℃)。从这些数值中，可以看出2点：中层异常类型的合成CE与AE的最大，其次是浅层异常类型，最后是深层异常；每一类的合成AE的温度异常最大值都比相应类别的合成CE的异常值要大。

图9(b),(d),(f)为3类合成CE(蓝线)和AE(红线)的盐度异常平均垂直剖面图。从图中可得到，浅层异常类型的合成CE(AE)的盐度异常在194 m(223 m)处达到最大为-0.25(0.15)，在海水深度480 m(460)以上调制为负(正)S′，但在下方调制为正(负)S′。中层异常类型的合成CE(AE)的盐度异常S′在338 m(335 m)处达到最大为-0.28(0.22)，在海水深度627 m(585 m)以上调制为负(正)S′，但在下方调制为正(负)S′。深层异常类型的合成CE(AE)的盐度异常S′在504 m(496 m)处达到最大为-0.13(0.05)，在海水深度744 m(700 m)以上调制为负(正)S′，但在下方调制为正(负)S′。因此，与温度异常类似，中层异常类型合成CE与AE的S′最大，其次是浅层异常类型，最后是深层异常类型。最后，可以看到AE和CE的T/S异常剖面几乎是彼此的镜像反射。

图9右侧从上到下依次是浅层异常、中层异常以及深层异常的CE、AE的Argo剖面的分布密度图。浅层异常的剖面主要分布在KE北部；中层异常剖面主要分布在KE流轴两侧；深层异常剖面主要分布在黑潮延伸体区域的西南部。从整体上来看，大幅度、大面积的AEs和CEs分别在黑潮延伸体区域流轴的北边和南边。

3.3 不同类型中尺度涡旋空间分布及水下特征对比

从图9分类结果的垂直结构与空间分布可以反映出KE区域涡旋异常随着经向和纬向变化。涡旋最大温度异常所在的深度沿经向发生变化。在黑潮延伸体北部区域，涡旋的异常影响深度较浅，以表层异常类型的涡旋为主。这种类型的涡旋大部分集中在35°N以北，160°E以西区域，只有部分较弱的暖涡会延伸到160°E以西，但仍然分布在黑潮延伸体的北部区域，深层异常的AEs与CEs主要分布在研究区的西南部，这与Dong等[19]分析的涡旋垂直结构的空间变化是一致的，他认为这与KE区域南北向不同背景层理是一致的，其动力机理可能是分别与亲潮冷水的入侵及当地复杂的海洋地形及流场环境相关。

对于区域变化，东部区域以弱异常信号为主，强异常信号更多的聚集在西部区域。在图9中甚至可以发现强异常与弱异常有明显的东西分离的特征。KE以南的AEs信号明显向西逐渐增强，其原因可能是受以向西深化的等密度梯度为特征的背景层理的影响，以及在更远的西部产生了更活跃的旋涡和更深层的异常，而此处的KE射流也更活跃。针对流轴两侧的涡旋，尤其是强异常信号主要明显的分布在流轴的两侧。这与Itoh等[13]用高度计探测到的大振幅信号相吻合。AEs出现在黑潮延伸体北侧，而CEs出现在黑潮流轴的南侧。这种类型的涡旋通常认为是从黑潮延伸体中脱落而来，多数学者认为是黑潮流轴的不稳定性质所造成[14，29]。以上分类结果与之前研究成果的一致性，充分说明了本文分类结果的合理性。

为了说明合成CEs和AEs的垂直结构，图10给出了穿过合成涡旋中心沿子午线方向的合成涡旋垂直切面。图10左侧(右侧)从上到下依次是CE(AE)内的Argo剖面浅层、中层、深层垂直温度异常的合成结果。从图10合成结果来看，CE与AE浅层异常主要在水下200 m左右，冷异常(暖异常)最大值为-3(3)；CE与AE中层异常主要在水下400 m左右，冷异常(暖异常)最大值为-4(4)；CE与AE深层异常主要在水下550 m左右，冷异常(暖异常)最大值为-2(2)。可以看出，合成涡旋对海洋物性参数的影响在垂直方向上主要局限在800 m以上。虽然影响可以达到1 000 m，但在800 m以下影响很小，可以忽略不计。

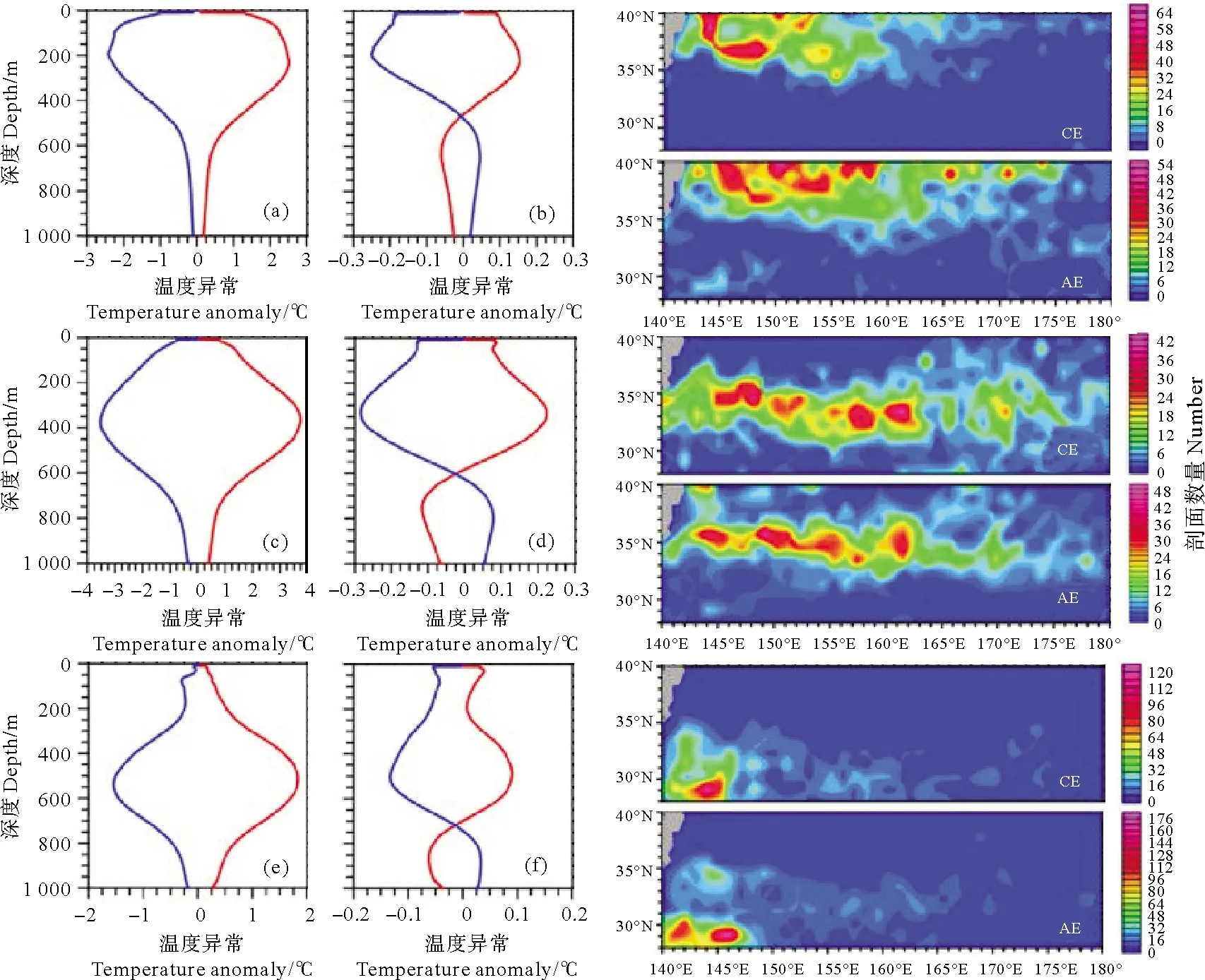
(红(蓝)线是三种合成AE(CE)内Argo剖面平均值；右侧是合成类型涡旋内部Argo剖面的分布密度图。 Redline(and blue) line are the average value of Argo plane in the three synthetic AE(CE). Right plots: the distribution density map of each type of profiles located inside the eddies.)

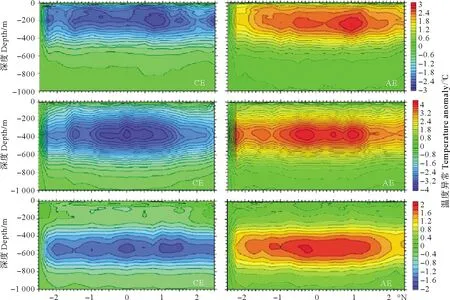
(左图：三种合成CE；右图：三种合成AE。 Left plots: the composite three types of CE; Right plots: the composite three types of AE.)图10 沿经向方向穿过合成涡旋中心旋的温度异常垂直剖面图Fig.10 Vertical sections of temperature anomaly of the composite eddies which cross the composite eddy’s center meridionally

4 结语

本文主要在140°E和160°E之间的KE射流路径上发现了中层异常的AEs和CEs最大的温度和盐度异常震级，中层异常的合成CE(AE)的温度异常最大值是在379 m，为-3.5 ℃(410 m，1.78 ℃)，CE(AE)的盐度异常最大值是在338 m，为-0.28(335 m，0.22)。Sun等[2]最近发现了KE区域内合成CE(AE)最大冷(暖)异常在360 m，为-2 ℃(410 m，1.78 ℃)；合成CE和AE在260 m处的最大盐度异常值分别为-0.13和0.12。这些数值都在我们合成结果的范围内，但是比我们结果的异常值小，这是因为我们的分类方法将流轴周围的强异常剖面自动地分为了一类，比用整体直接取平均的异常数值更大。其次，异常程度较弱的是浅层异常的合成涡旋。最后，深层异常这一类的异常程度最弱，KE区域南部的涡旋主要向西运动，异常程度逐渐降低。图10的垂直切面的温度异常结果更明显清晰地显现出CE(AE)浅、中、深三类异常的最大异常深度以及最大异常值，更清晰地显现出CE(AE)浅、中、深三类异常的最大异常深度以及最大异常值。

本文将GMM无监督聚类方法应用于KE区域涡旋内部的Argo温度异常剖面，以此对KE地区的涡旋进行分类。聚类结果表明，KE区涡旋垂直结构的空间变化与Dong等[19]的结果一致。其次，气旋涡和反气旋涡两种类型的最大温度异常都出现在中层异常类，分布在KE的流轴周围。这种模式与Itoh等[13]的高度计检测到的冷芯环和暖芯环的空间分布一致。这表明GMM聚类方法对于客观地自动分类不同垂直结构的涡旋颇为有效。随着Argo剖面数据的积累，这种基于Argo异常剖面的中尺度旋涡无监督分类方法将应用于其他海洋区域，海洋科学家可以方便地对特定类型海洋漩涡的三维结构、动力学及其影响进行有价值的科学研究。