多虚拟电厂博弈的区域电网经济调度

邱革非，余欣蓉，金乐婷，何 超，娄 阳，杨翱瑜

（昆明理工大学电力工程学院，昆明 650500）

由于分布式电源DG（distributed generation）所处的位置较为分散，独立设备发电容量较小，因而缺乏集中控制的条件。为了解决分布式电源不能集中控制的问题，微电网、虚拟电厂等概念应运而生。虚拟电厂VPP（virtual power plant）可以将独立的分布式电源聚合起来统一参与电力市场。更准确地说，VPP可以将一定范围内的分布式电源、负荷（可中断和不可中断负荷）和储能系统结合，通过统一的调控中心，合并为一个整体参与电力市场[1]。VPP主要可以分为两种类型：一种是商业型虚拟电厂CVPP（commercial virtual power plant），另一种是技术型虚拟电厂TVPP（technical virtual power plant）。CVPP是商业聚合，主要考虑VPP以整体形式参与市场交易的情况，有效减少分布式电源单独竞标的风险，通常情况下不考虑对配电网可能带来的影响；TVPP一般由同一位置的分布式电源组成，除了可代表分布式电源整合后的整体技术特性和成本信息之外，还可提供电网调节、功率平衡等功能，需计及其对配电网的影响。

在一个包含虚拟电厂的区域电网中，可以通过经济调度，一方面保证电网安全运行，另一方面优化电网中各方经济利益，提高收益。经济调度可分为短期经济调度和长期经济调度，短期经济调度是指电网未来数小时、一日或数日的出力安排，长期经济调度是指电网未来数周、数月或数年的出力安排。含VPP电网在进行经济调度时，融合了物理、价值等多种要素。在各VPP中标量可进行重组的基础上，VPP通过参与市场竞争可实现价值增值[2]。

近年来，含VPP电网的经济调度问题[3-12]吸引了相关领域研究人员的关注，发表了若干研究成果。其中文献[3]考虑了一种基于配电网安全性的虚拟电厂非合作博弈模型，为了保证配电网较好的安全性，同时计及VPP需取得较大利润，相对削减了VPP的发电量。文献[6]利用多代理技术构造了含虚拟电厂的电力系统日前竞价以及优化模型，VPP以自身利润最大为目标参与系统运行，系统以社会效益最大为目标函数进行经济调度。文献[7]建立了VPP同时参与多类电力市场的三阶段竞价模型，同时计及了电动汽车和需求响应的影响，进行经济调度，减少了VPP的运行成本。文献[9]采用虚拟电厂模式聚合热电联产机组，以虚拟电厂自身利润最大为目标进行优化调度，同时计及用户舒适度的影响，实现热、电协调优化运行。文献[11]设计了一种虚拟电厂同时参与能量市场和备用市场的优化调度模型，实现VPP经济效益最大。上述文献对研究含VPP的电网经济调度做出了贡献，这些研究只考虑VPP作为价格接受者，被动地根据上层电网决策调整内部运行状态，没有考虑在市场比较成熟时，VPP将作为市场主体参与市场竞争以获得更高收益。

为了解决上述问题，本文提出了一种多VPP非合作博弈的区域电网经济调度方法。本文算法构造了一个两层优化模型。上层各VPP作为价格制定者，通过改变各VPP的策略报价系数，以各VPP利润最大为目标，各VPP内部成员可自我调节来响应VPP整体对外的运行要求；电网层是市场出清模型，电网以购电成本最小和有功网损最小为目标确定各VPP的中标量及市场出清电价。最后通过算例仿真分析，验证本文提出方法的可行性和有效性。

1 多VPP博弈的电网双层经济调度模型

本文构建了一种多VPP非合作博弈电网双层经济调度模型，首先各VPP进行初始报价，将报价函数及出力范围上报给电网，电网以购电成本及有功网损最小为目标进行市场出清，求得出清电价及各VPP的中标量，然后VPP根据出清电价及各自的中标量求出各自的利润，VPP随后进行报价策略调整以争取更多利益，每次在假设其他VPP竞价策略不变的基础上改变一个单独的VPP报价策略，重新出清并计算各VPP的利润，直到满足收敛条件为止。具体的流程如图1所示，图中r表示每轮迭代次数，s表示轮数。

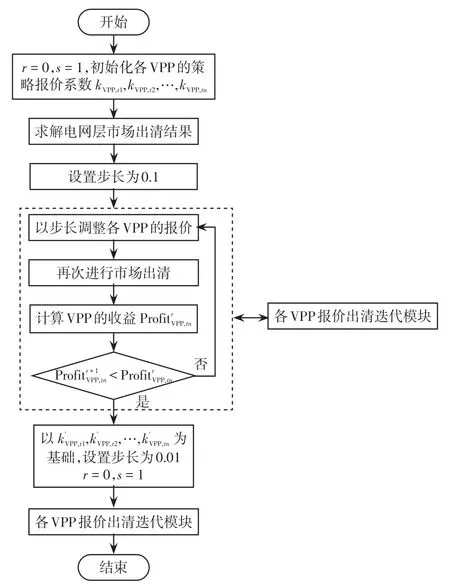
图1 多VPP非合作博弈的电网双层经济调度Fig.1 Multi-VPP non-cooperative game for dual-level economic dispatching of power grid

本文所介绍的双层经济调度模型不仅计及了电网运行的安全性和经济性，还有利于VPP获得最大利润。从电网的角度出发，目标函数考虑了有功和无功两方面的问题，同时计及购电成本和有功网损最小，考虑问题更加全面；从VPP的角度出发，VPP进行非合作博弈竞价，在已知对方竞价策略的基础上，合理制定自身的报价策略，有利于增加自身获得的利润。

2 VPP调度模型

2.1 关于VPP的分析条件设定

（1）本文研究的VPP是TVPP，即VPP从电网管理的角度综合考虑一定的约束条件作为一个独立的个体参与电力市场交易[13]，同时计及VPP的交易情况对电网所造成的影响。

（2）假设VPP内部所有DG机组都是可调度的，每个DG的成本函数是其实际功率输出的函数。

2.2 VPP的成本

因为本文考虑的TVPP出力特性通常由内部DG的出力决定，同时计及内部负荷和储能的影响，因此由设定条件（2）可知VPP的发电成本与发电量有一定的关系，可以根据发电机发电量及成本关系构建VPP发电量关于发电成本的函数关系式，即

式中：Cost(p)为发电商的成本函数；p为发电商在现货市场的发电量；a为发电商的空载成本系数；b为发电商的起始边际成本系数；c为发电商边际成本系数，2c为价格曲线的斜率，一般c＞0。

在发电商只参与现货交易市场的情况下，发电商可建立边际成本关于发电量的一次函数，即

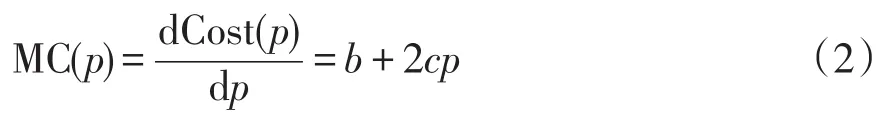
式中，MC(p)为发电商的边际成本函数，在本文中的定义是发电商每出力1 MW所产生的成本。

本文发电商作为价格制定者，是不会严格按照边际成本进行报价，但可以围绕边际成本进行报价，因此可以引入一个策略报价系数k，则发电商的报价为

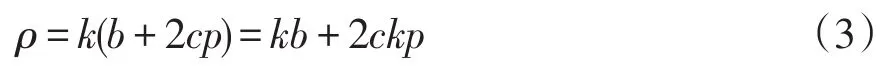
式中，2ck表示发电商的投标斜率。

以上描述VPP发电成本与发电量之间的关系近似为线性函数，即

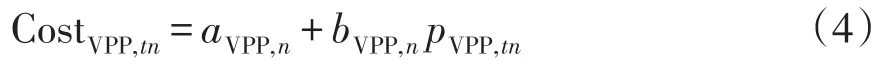
式中：CostVPP,tn表示第n个VPP第t小时的成本；pVPP,tn表示第n个VPP第t小时的发电量；aVPP,n、bVPP,n表示第n个VPP的边际成本系数。

则VPP的报价可以在发电成本的基础上乘以一定的策略报价系数，VPP的报价函数为

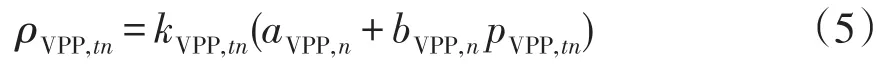
式中：ρVPP,tn表示第n个VPP第t小时的报价；kVPP,tn表示第n个VPP第t小时的策略报价系数。

2.3 VPP的数学模型

VPP在售电竞价过程中，为实现利润最大化，设在一天（24 h）时间断面内，其目标函数为

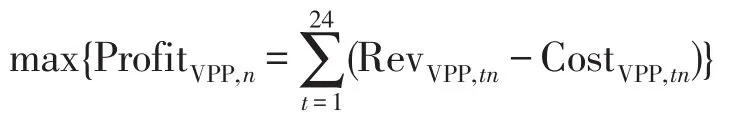
式中：ProfitVPP,n为第n个VPP一天的利润；RevVPP,tn为第n个VPP第t小时的收益；PVPP,tn为第n个VPP第t小时的中标量；λVPP,tn为第n个VPP第t小时的市场出清电价。

如果VPP处于完全竞争的电力市场，则以边际成本进行报价将获得最大利益。但实际上电力市场是一个不完全竞争的寡头垄断市场，由于市场信息不完整等原因导致市场竞争的参与者并不会直接按照边际成本进行报价，而是围绕边际成本来确定竞争价格。因此，在式（4）的基础上引入策略报价系数，其上、下限约束为

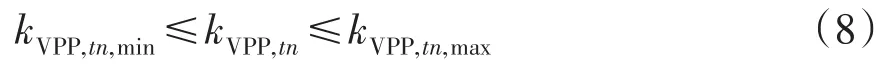
本文VPP作为价格制定者，其中标量和市场出清电价都是由所有VPP的报价共同决定，分析式（5）可知策略报价系数的变化会使VPP报价发生变化，因此推得策略报价系数的变化会引起各VPP中标量以及出清电价的变化。

3 电网层的调度模型

电网层的调度主要以电网总购电成本最小为目标函数，同时计及网损最小，综合考虑电网功率平衡、节点电压上下限和联络线功率上限等约束条件，进行经济调度。本文只研究VPP的竞价，暂时忽略其他发电商。

3.1 确定权系数

下层的目标函数为

式中：nl为所有支路的总和；Pij,t为第t小时节点i和节点 j之间的有功网损；v1为电网层以购电成本最小为目标函数的权重；v2为电网层以有功网损最小为目标函数的权重。

本文采用α法确定权系数，主要过程如下。

（1）设电网层的调度模型由两个目标函数组成，将式（9）对应的优化问题分解成优化目标，即

（3）联立方程组求解，即

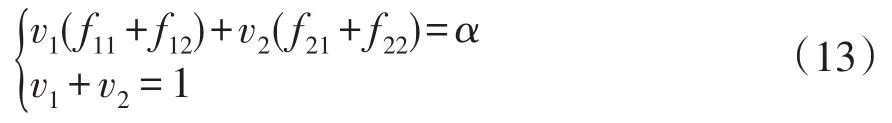
（4）求出权重，即

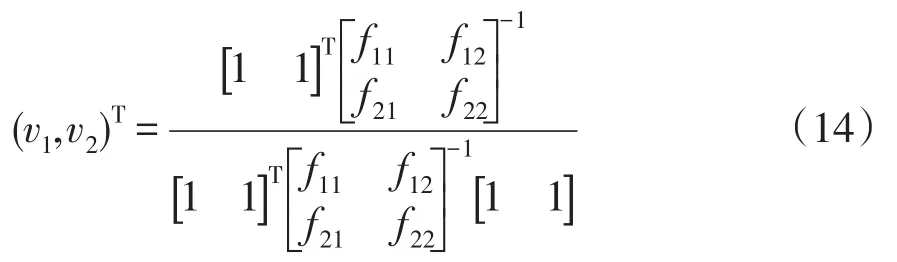
3.2 约束条件

1）系统功率平衡约束

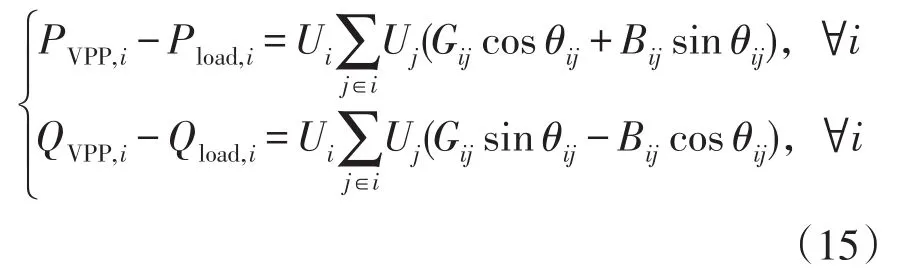
2）各VPP出力的上、下限约束

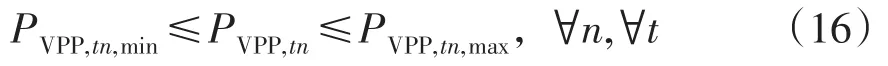
3）节点电压幅值上、下限约束

4）联络线功率约束

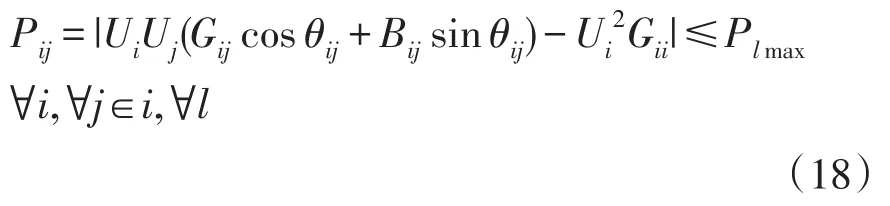
式中：PVPP,i、QVPP,i分别为节点i处的VPP输出的有功和无功功率；Pload,i、Qload,i分别为节点i处的有功负荷和无功负荷；PVPP,tn,min、PVPP,tn,max分别为第n个VPP第t小时出力的下限和上限值；Umin、Umax分别为节点i的电压幅值的下限和上限；Plmax是联络线l的功率上限。

4 电网层优化求解方法

电网层优化的控制变量主要是区域电网分配给各VPP的发电量及出清电价，在满足各种潮流约束的条件下，实现电网层购电成本和有功网损最小，这一层采用跟踪中心轨迹内点法的方法求解，其流程如图2所示。

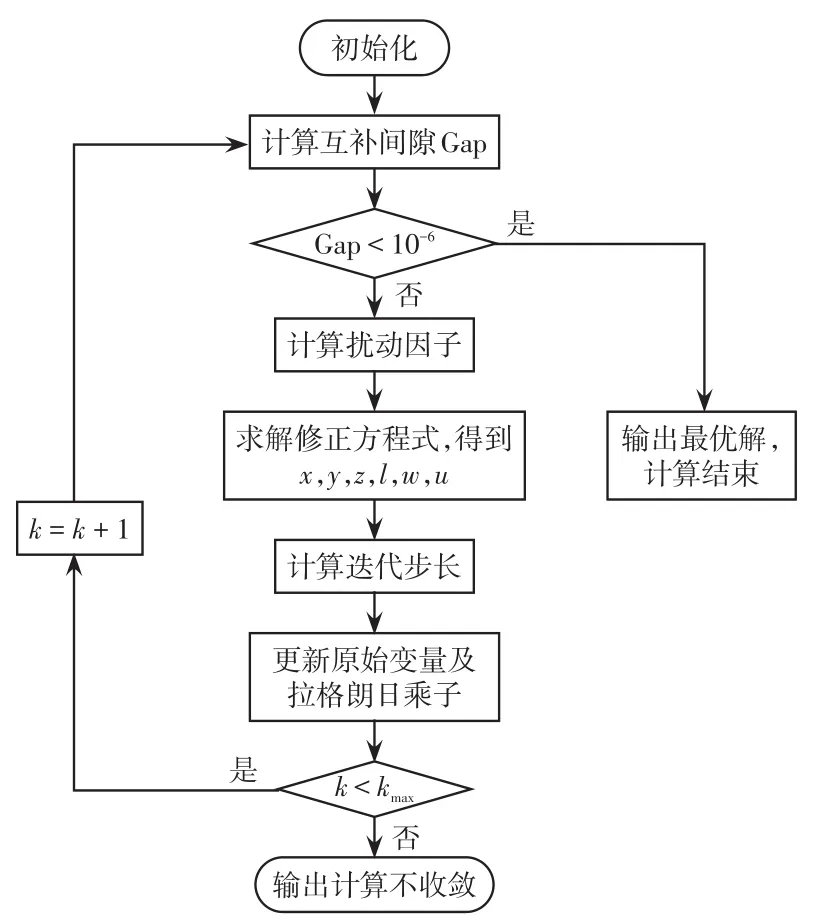
图2 跟踪中心轨迹内点法流程Fig.2 Flow chart of interior point method of tracking the center trajectory

其基本思路是寻优迭代过程始终在可行域内进行，初始点应取在可行域内，并在可行域的边界设置“障碍”使迭代点接近边界时其目标函数值迅速增大，从而保证迭代点都是可行域的内点[14]。

可将电网层目标函数转化为

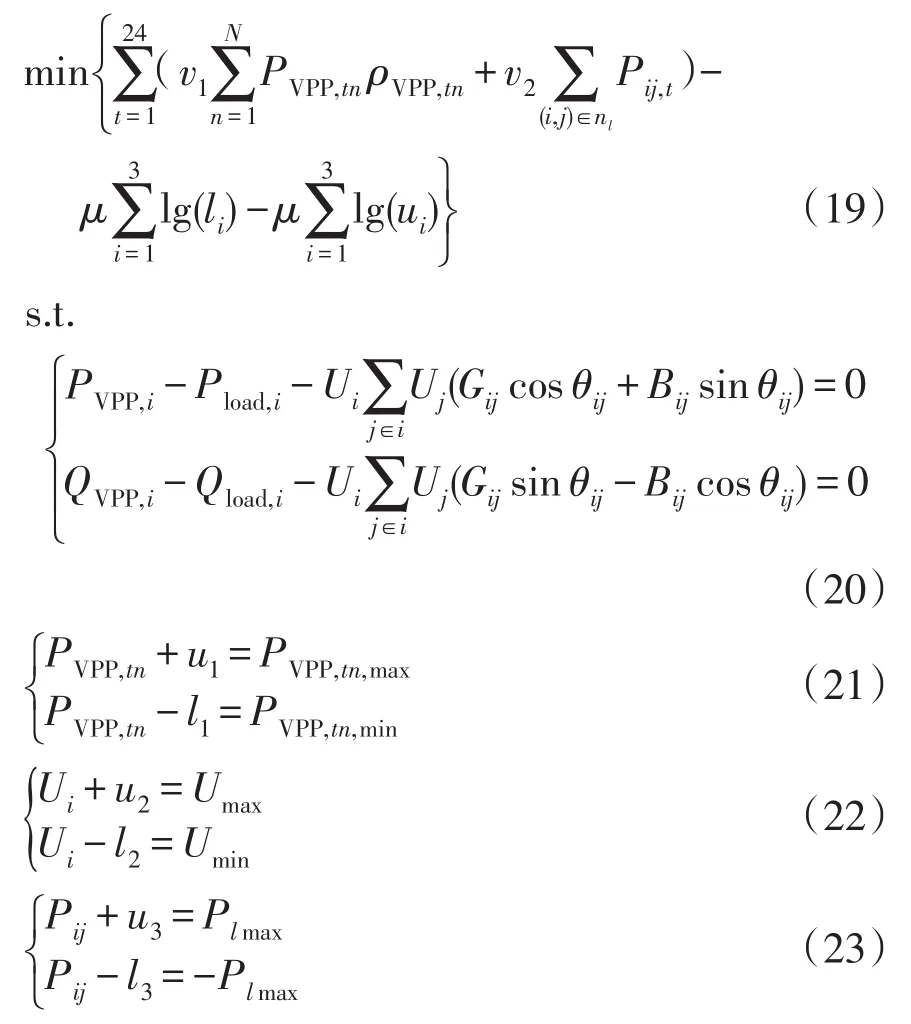
式中，μ为障碍常数（μ＞0），可将目标函数改造为障碍函数式。

可以将式（20）～（23）概括为

式中：g（x）为等式约束；h（x）为不等式约束。

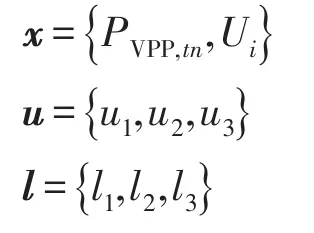
u和l都是松弛变量（u＞0,l＞0），其作用是将不等式约束转化为等式约束，和分别为不等式约束的上、下限。

式（19）的拉格朗日函数为

此问题极值的必要条件就是拉格朗日函数对所有变量和乘子的偏导数为0[14]，即

式中：e=[1,1,1]T；L=diag(l1,l2,l3)，其中diag(l1,l2,l3)表示对角元素为 l1、l2、l3的对角矩阵；U=diag(u1,u2,u3);Z=diag(z1,z2,z3);W=diag(w1,w2,w3)。

将式（26）～（36）线性化用牛顿法求解，迭代得到修正量，求得最优近似解。得出的结果就是区域电网分配给各VPP的中标量以及市场出清电价，VPP随后根据市场出清电价和预测其他VPP的竞价策略进行非合作博弈，调整自己的竞价策略，再次报价出清。

5 VPP非合作博弈竞价求解方法

5.1 非合作博弈模型纳什均衡点的存在性

根据定理[15]（当策略集合是Euclid空间的非空紧凸集，支付函数关于策略集合连续且拟凹，则该博弈存在纯策略纳什均衡），将策略报价系数和中标量作为VPP的决策变量，其策略集合表示为

显然这个策略集是非空集、凸集和紧集。

对式（6）进行求导。虽然式（6）中的出清电价有不同的形式，但式（6）的一阶导数可概括为如式（38）和式（39）两种形式。

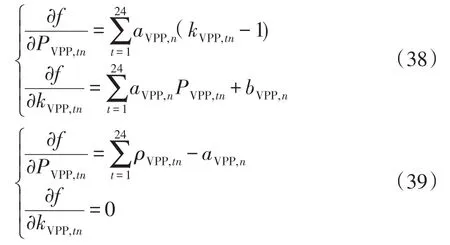
其二阶导数为

由于f的二阶导数都为0，因此式（6）为连续拟凹函数。

由此证明，多VPP非合作博弈的纳什均衡点存在且唯一。

5.2 非合作博弈模型的具体求解方式

5.2.1 非合作博弈模型求解的前提条件

（1）本文研究的VPP作为价格制定者。

（2）假设各VPP全部参与电力市场竞价，并且各VPP可以预测对方的竞价策略。

（3）假设在非合作博弈过程中，VPP可以选择高价和低价两种竞价策略[16-19]，既可以采用高价策略抬高市场电价来增加自身利润，也可以采用低价策略出售更多电量来增加自身利润，但无论是哪种策略，其报价都不可能低于自身成本。

（4）假设非合作博弈过程中，每次只改变一个VPP的竞价策略，其他VPP的竞价策略固定。

5.2.2 非合作博弈达到纳什均衡的判断条件

各VPP可以根据其发电成本和竞价策略决定自己的策略报价系数，改变自己的报价，从而影响市场出清结果。而某个单独VPP竞价策略的改变也会促使其他VPP改变其竞价策略，进而使整个系统的利益重新分配[20]。

对于一个虚拟电厂VPPn，可用以下集合式子Jn={ρVPP,n1(t),ρVPP,n2(t),…,ρVPP,ni(t),…,ρVPP,nm(t)} 表 示虚拟电厂n在t时刻的m种策略集合，ρVPP,ni(t)表示虚拟电厂n在t时刻的第i种策略，VPPn可以根据市场出清模型求出VPPn的中标量及出清电价，从而得出收益ProfitVPP,ni。

当所有VPP改变自己的竞价策略都不能增加自身的最大利润时，即满足式（41），则达到纳什均衡。

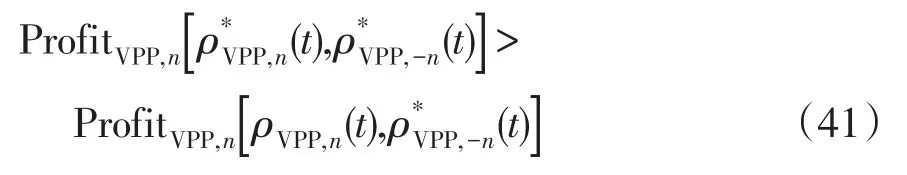
式中：“*”表示 VPPn 的最优报价；“-n”表示除n之外其他参与非合作博弈竞价的虚拟电厂。

5.2.3 非合作博弈达到纳什均衡的具体求解步骤

本文以若干个不同的VPP参与非合作博弈为例，在博弈过程中，采用改变策略报价系数的方法找到纳什均衡点。首先以较大步长进行迭代找到VPP的利润转折点，发现转折点后退回上一点采用较小步长进行搜索，最后求得纳什均衡精确点。具体步骤如下所述。

6 算例分析

本文将IEEE9节点作为仿真系统，在节点1、2、3分别接入3个不同的VPP，具体参数如表1所示。

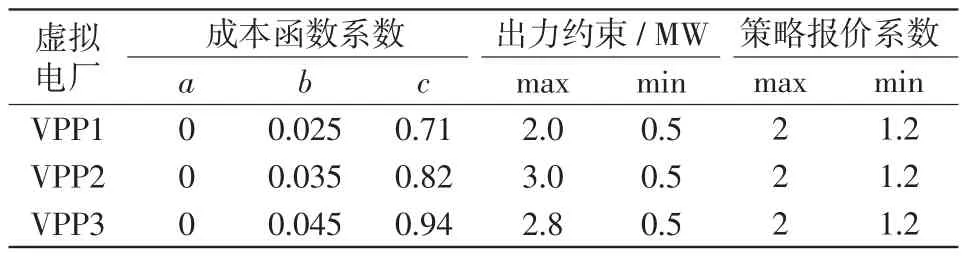
表1 各VPP的具体参数Tab.1 Specific parameters of each VPP

以一个调度周期的竞价过程为例，设定3个VPP的初始策略报价系数都为1.2，日前现货市场的调度周期为1 h。在示例调度周期内的负荷需求为2.65+1.5 MV·A，区域电网中各节点的电压幅值上下限都为0.95～1.05 p.u.。

3个VPP先上报初始报价，电网层以购电成本最小以及网损最小为目标进行市场出清，确定电网分配给各VPP的发电量，计算结果如表2所示。其中购电成本和网损的权系数用α法确定，由式（14）得v1=0.755，v2=0.245。

表2 各VPP的初始市场出清结果Tab.2 Initial market clearing results for each VPP

随后各VPP对自身的竞价策略进行修正，单个VPP考虑到其他VPP竞价策略对自身报价的影响，合理制定自身的竞价策略。这里运用了控制变量法的思想，每次只改变单个VPP报价，其他VPP报价固定，将多VPP利润最大问题转化成多个单独VPP利润最大问题，分别研究每个VPP利润最大所对应的点，最后综合解决。从图3～图5可以看出在第一次寻优过程中，3个VPP的净利润都是先增大后减少，因此图中的转折点就是每个VPP利润最大化的点，这个点与多重因素（各VPP的成本系数、策略报价系数、中标电量等）有关。

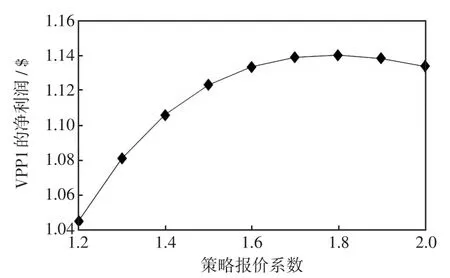
图3 VPP1以0.1为步长迭代所得净利润Fig.3 Net profit of VPP1 obtained by iterating at a step size of 0.1

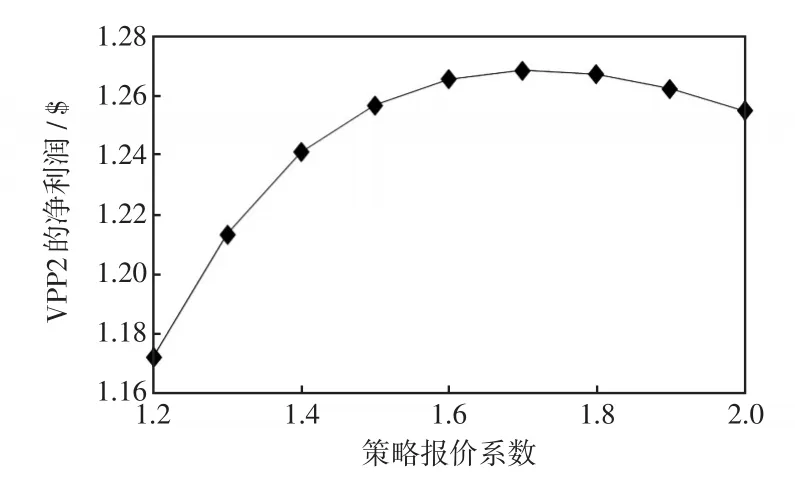
图4 VPP2以0.1为步长迭代所得净利润Fig.4 Net profit of VPP2 obtained by iterating at a step size of 0.1

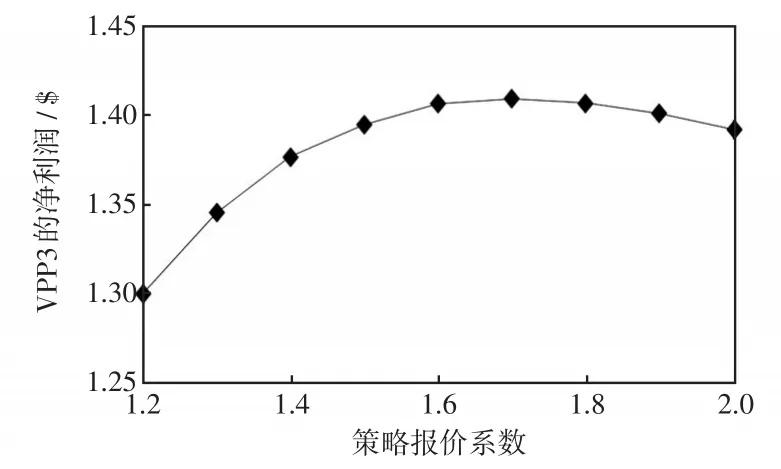
图5 VPP3以0.1为步长迭代所得净利润Fig.5 Net profit of VPP3 obtained by iterating at a step size of 0.1

表3～表5结果显示各VPP达到利润最大时的策略报价系数取值是不同的。其中，VPP1的最优策略报价系数为1.80，VPP2的最优策略报价系数是1.70，VPP3的最优策略报价系数是1.70，对应的中标量分别为0.794MW、0.800MW和0.785MW，对应的报价分别为2.074$/（MW·h）、2.289$/（MW·h）和2.586$/（MW·h）。

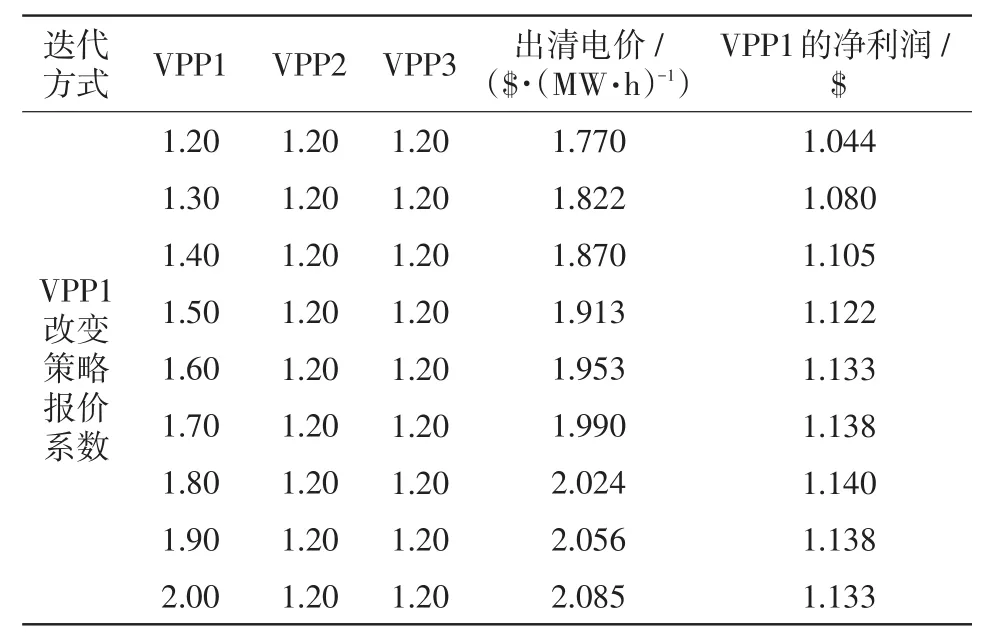
表3 VPP1以0.1为步长迭代结果Tab.3 Result of VPP1 by iterating at a step size of 0.1

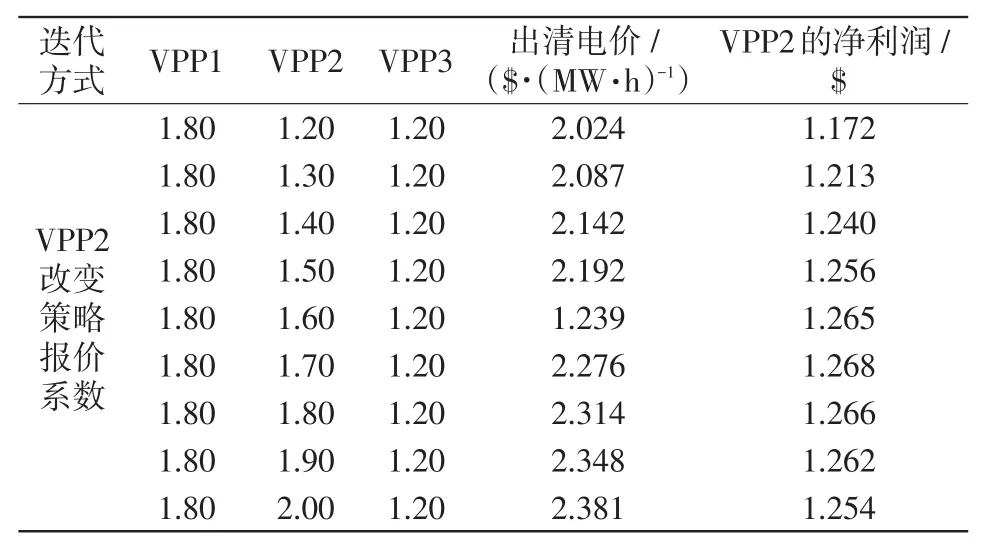
表4 VPP2以0.1为步长迭代结果Tab.4 Result of VPP2 by iterating at a step size of 0.1

表5 VPP3以0.1为步长迭代结果Tab.5 Result of VPP3 by iterating at a step size of 0.1

各VPP第二次寻优迭代结果如表6所示。

与第一次竞价寻优相比，第二次迭代结果更加精确，各VPP取得最大利润所对应的策略报价系数分别是1.80、1.73和1.70。

由表2和表6所得，各VPP采用变步长非合作博弈竞价方法所得的净利润都有所增加，其中VPP1的净利润增加了0.799$，VPP2的净利润增加了0.718$，VPP3的净利润增加了0.639$。因此本文所使用的变步长非合作博弈方法具有优越性，使每个VPP的净利润都能相对增大。运用此种方法，从VPP所获中标量的角度出发，使VPP1的中标量有所减少，而VPP2和VPP3的中标量相对增加；从VPP最优报价的角度出发，使VPP1、VPP2和VPP3所对应的最优报价都有所上升。

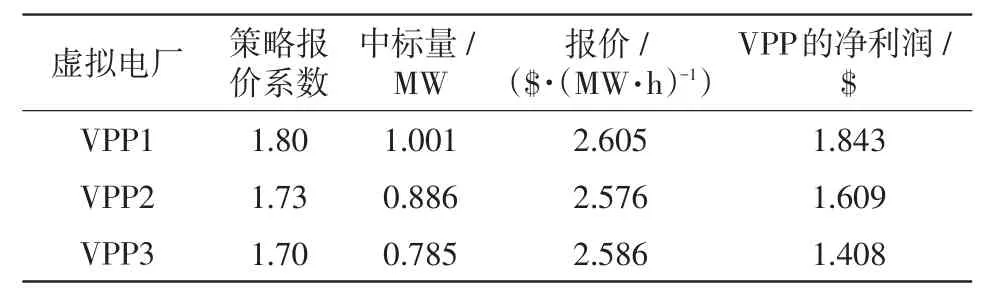
表6 各VPP以0.01为步长迭代结果Tab.6 Result of each VPP by iterating at a step size of 0.01

因此，VPP采用变步长非合作博弈竞价方法能显著增加不同VPP自身的利润，使电力市场交易更合理，更符合实际。

由表7可得，博弈后的总购电成本增加了2.171$，总网损增加了0.387 kW。已知在采用变步长非合作博弈竞价方法后，各VPP所获净利润都有大幅度的增加，由于本文介绍的调度模型不仅需实现各VPP利润最大化，还需实现电网购电成本和网损最小化，在一定程度上这两层目标不能同时达到最优，需在两者之间找到一个平衡点，因此各VPP所获净利润增加的同时电网作出了让步，即购电成本和网损增加，使两层的目标达到一定范围内的最优。

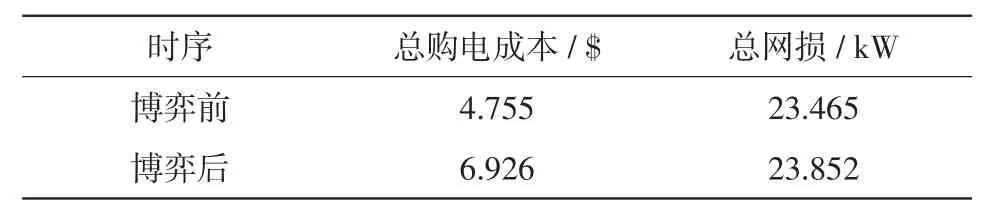
表7 博弈前后总购电成本及网损Tab.7 Total power purchase cost and network loss before and after game

7 结论

本文基于一个两层优化模型，上层在改变各VPP策略报价系数的基础上，以各VPP利润最大为目标提出了一种非合作博弈竞价实现方式，电网层综合考虑购电成本以及有功网损最小，实现市场出清，两层结果相互迭代，通过IEEE9节点的仿真实例，得出如下结论：

（1）双层调度方法既保证了电网运行的经济性、安全性，也使得各VPP在参与电力市场竞价过程中不能随意抬高报价，只能围绕边际成本进行报价，保证了电力市场的公平性、合理性；

（2）以单独改变各VPP策略报价系数为基础进行报价，利用变步长方法搜寻纳什均衡点，优化VPP报价策略的方法在求解VPP非合作博弈问题中确实可行。

需要指出的是，本文所提出的非合作博弈竞价方法对如何快速精确地找到纳什均衡点有参考意义，但VPP博弈均衡点在不同条件下有不同的表达方式，在决策和求解算法上可做进一步的改进。