角加速度平滑的可变类圆周下肢康复步态规划

陈琳，夏凯，张学涛，杨思创,2，潘海鸿

1.广西大学机械工程学院，广西南宁市 530004；2.广西南宁丁一科技有限公司，广西南宁市530004

下肢康复机器人通过引导偏瘫患者进行定向功能训练，强化患者的外周深、浅感觉输入刺激，促进患者下肢的恢复，最终恢复步行[1-4]。康复治疗过程中，合理的步态规划轨迹对患者的康复效果有重要影响[5]。步态规划是指设计康复训练轨迹，控制各个关节的运动[6-7]。

对于坐、卧式下肢康复机器人，步态规划常采用模型法，即通过建立下肢康复机器人运动学模型，根据腿部末端轨迹，逆运动学求解得到各关节角度[8]。在机器人运动过程中，笛卡尔空间和关节空间的运动平稳性都需要考虑[9]。张立勋等[10]研发一种四自由度踏板机构，采用的可调步态规划方法以步长、步态周期和步态时相为参数，并使用Matlab/Simulink 仿真求解椭圆轨迹。史小华等[11]在坐/卧式截瘫下肢康复机器人上设计圆周轨迹，使用Adams 仿真得到关节角度、速度、角加速度曲线。张冬[12]对末端任意曲线轨迹进行分段多项式插值，得到关节空间的平滑轨迹，但在曲线复杂时插补后轨迹与原轨迹偏差过大。蒲明辉等[13]为保证末端轨迹速度连续，使用四次多项式对笛卡尔空间直线轨迹规划，但未考虑关节空间的速度、加速度连续。

因加速度突变会使得机器人运行时产生冲击，对患者康复训练效果造成不利影响，严重者甚至造成二次伤害。为此，提出一种类圆周步态轨迹模型，该模型使用五次多项式对每个周期关节角度曲线的起始段和结束段进行优化，使周期衔接时的角加速度、角速度平滑过渡；引入优化比例参数ratio，确定起始段和结束段的时间区间且大小可调，得到不同形状的类圆周末端轨迹；并在本课题组自主研发的多位姿下肢康复机器人上进行周期衔接时角加速度平滑的实验验证。

1 类圆周步态求解

1.1 下肢外骨骼及圆周步态轨迹模型

自主研发的下肢康复机器人单侧结构如图1(a)所示，其简化模型如图1(b)所示，末端圆周步态轨迹如图1(c)所示。

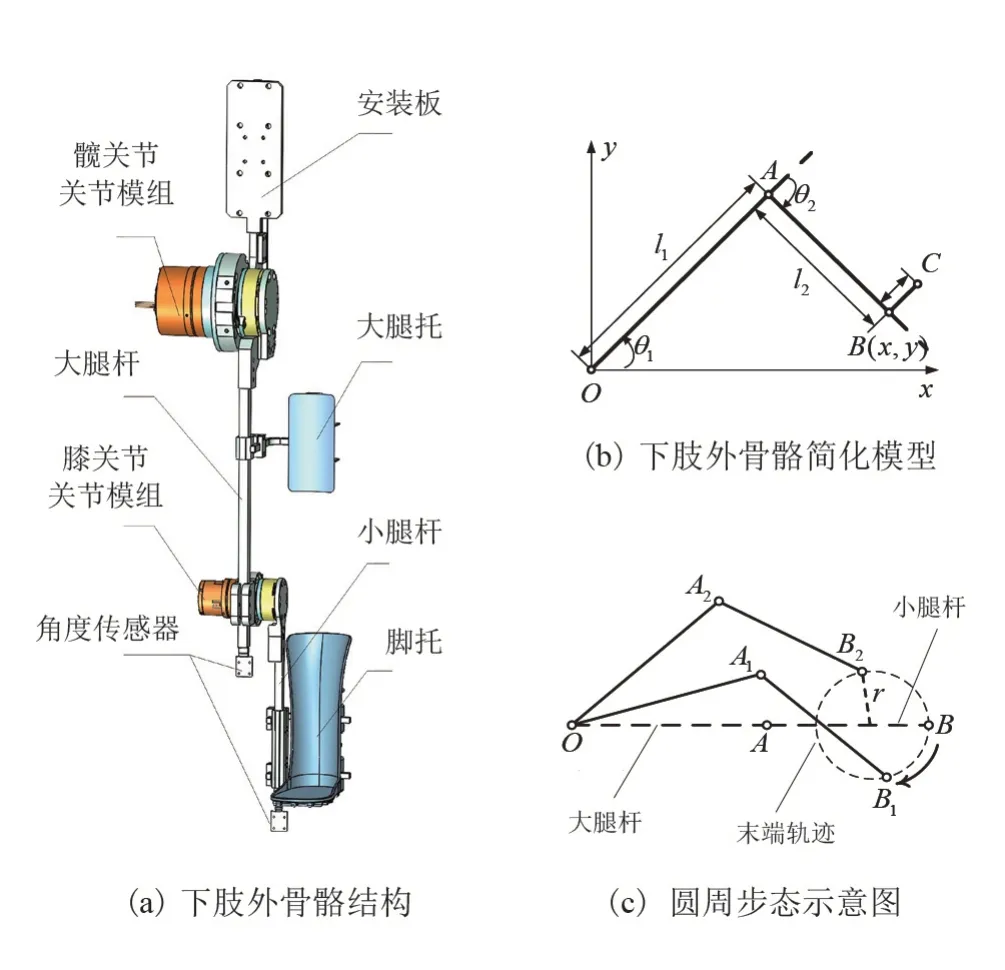
图1 下肢外骨骼及其简化模型

末端轨迹即点B的坐标(x,y)与θ1、θ2存在以下几何关系：

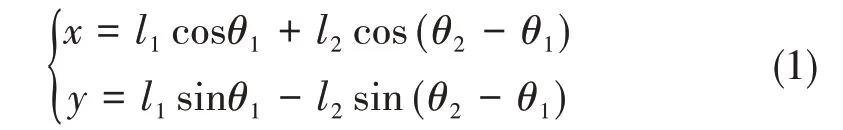
式中l1、l2分别为大腿长度和小腿长度。末端圆周的圆心位于OAB所在直线上，r为圆周半径，表征运动幅度。则圆周步态末端轨迹圆参数方程为：

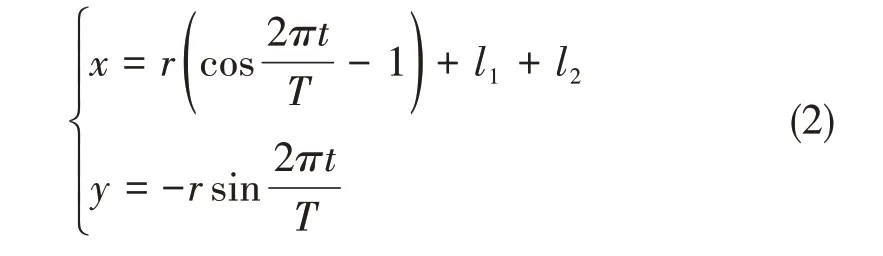
式中，t代表时间，T代表周期。

则一个圆周步态周期T内的髋关节角度θ1(t)和膝关节角度θ2(t)为：

圆周步态连续运动两个周期时，发现关节速度曲线在两个周期衔接处会产生加速度突变(因为圆周步态在起始速度和结束速度均大小不同，方向相反)，导致下肢康复机器人腿部发生抖动。

1.2 类圆周步态轨迹模型

为使下肢康复机器人在步态周期衔接时运动过程平稳(角速度、角加速度连续)，提出类圆周步态轨迹模型，该步态的一个周期关节运动轨迹分为三段：起始段、中间段和结束段，且起始段和结束段时间区间大小相同。起始段和结束段采用五次多项式进行轨迹规划，中间段仍保留圆周步态轨迹。

对一个周期运动轨迹进行等时插补时，设定周期为T，插补点个数为i，则插补周期Δt为：

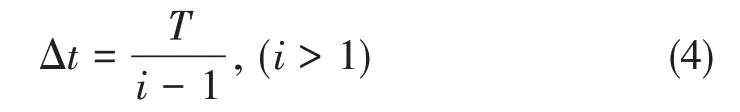
假设0～ts、te～T分别为类圆周步态轨迹的起始段和结束段，则引入比例系数ratio确定时间节点为ts，te：

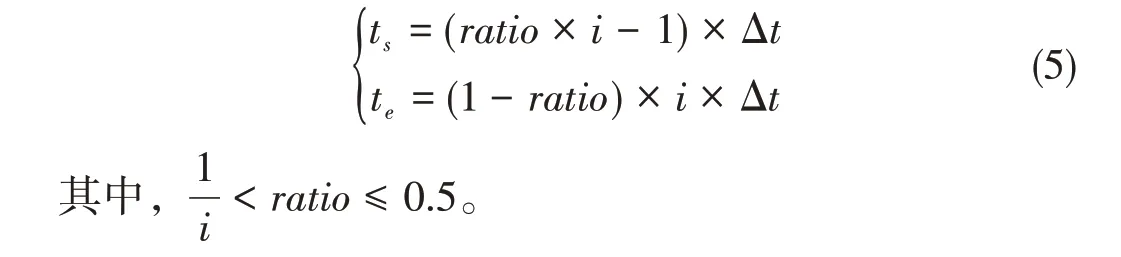
这两段轨迹采用五次多项式优化：

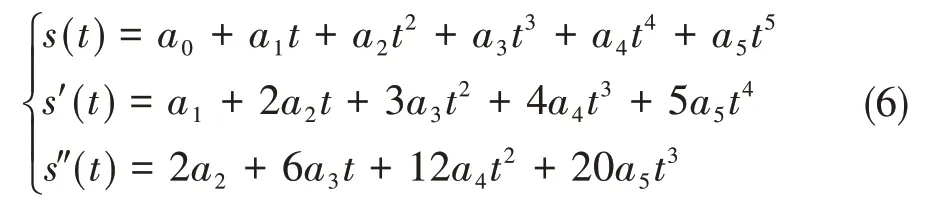
式中s(t)为关节角度，s′(t)为关节角速度，s″(t)为关节角加速度，a0～a5为多项式系数。

假设t=ts、t=te时刻的角度、角速度、角加速度，分别记为θs、ωs、αs，θe、ωe、αe，为使机器人启停平稳，将t=0、t=T时刻的角度、加速度、角加速度值都设定为0。

当t=0、t=ts可知：

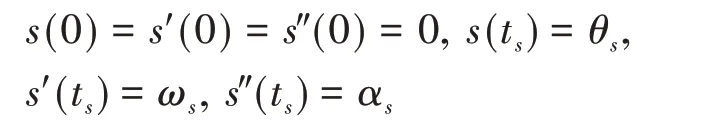
将其代入式(6)求解方程组可得0～ts段的五次加减速曲线的多项式系数as0～as5，同理可求得te～T段的系数为ae0～ae5。

由此建立髋关节的类圆周步态轨迹函数为：

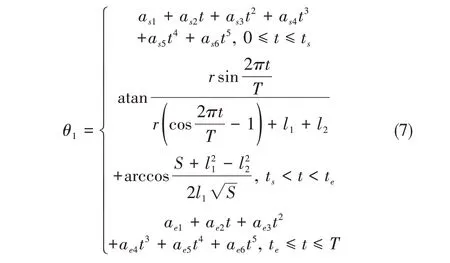
同理，可建立膝关节的类圆周步态轨迹函数。

2 类圆周步态仿真

根据《中国成年人人体尺寸(GB/T 10000-1988)》，选择年龄36～60 岁、身高1667 mm 的男性成年人人体尺寸进行运动数据计算，即大腿长l1=518 mm，小腿长l2=416 mm。

假设r=140 mm，T=8 s 的圆周步态，取比例系数分别为ratio=0.125、ratio=0.25、ratio=0.5，则由式(7)得到下肢各关节角度，角度-时间曲线如图2所示，可知ratio=0.125 时与圆周步态轨迹类似，但随着ratio变化，获得的类圆周步态轨迹的角度曲线不同。

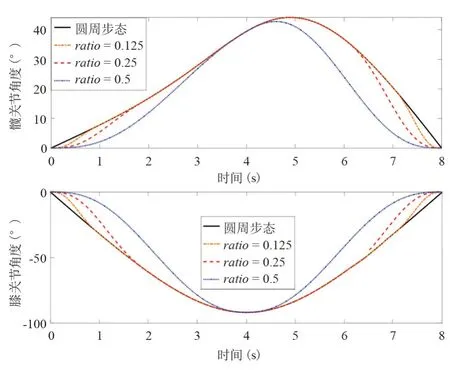
图2 圆周步态和类圆周步态理论关节角度曲线

求解出3 种ratio下的类圆周步态轨迹的关节角速度、关节角加速度并与标准圆周步态轨迹对比(图3和图4)。

由图3 可知圆周步态轨迹在关节空间的周期开始角速度和结束角速度大小不同，方向相反，因此在周期衔接时会发生角加速度突变(图4)。而3种不同ratio下的类圆周轨迹在关节空间的周期始末角速度为0，整个周期内角速度曲线光滑；且角加速度变化随ratio增加而更加平缓。

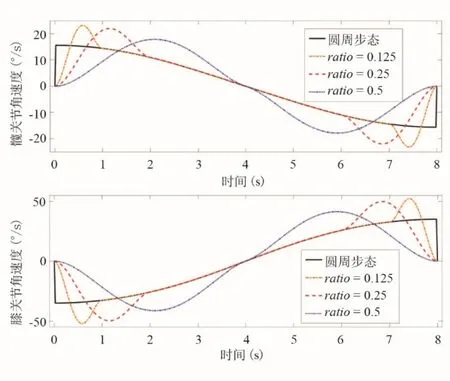
图3 圆周步态和类圆周步态理论关节角速度曲线

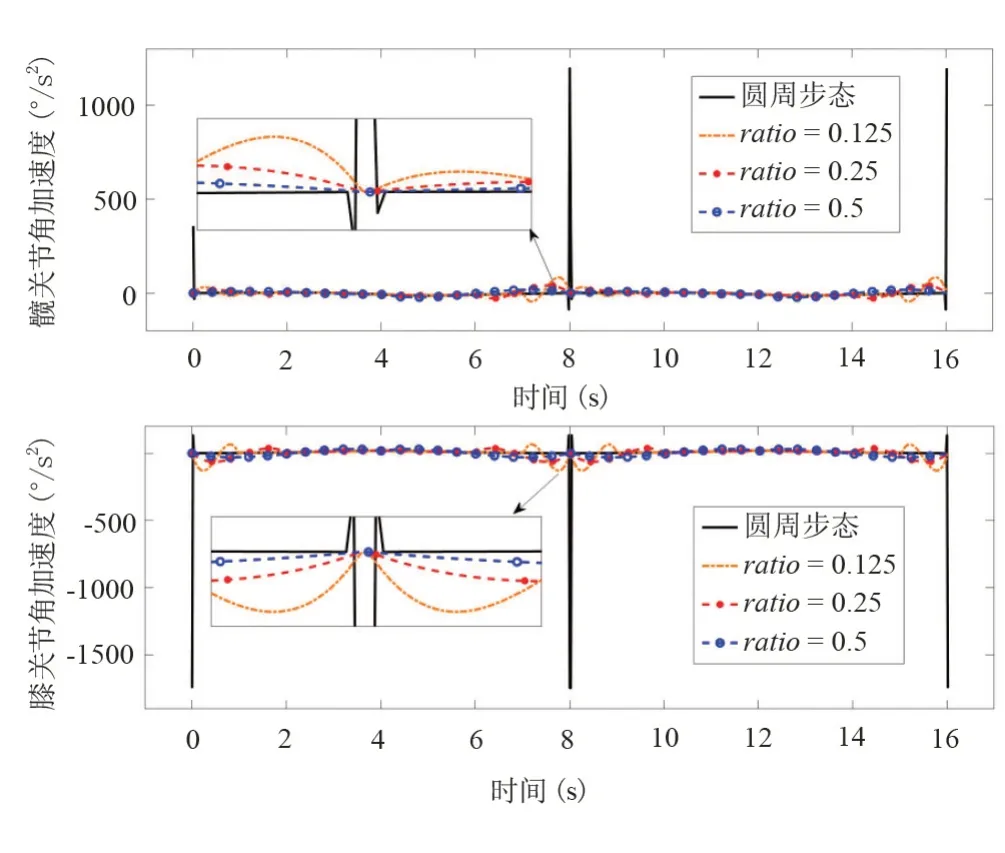
图4 圆周步态和类圆周步态理论关节角加速度曲线

3 实验验证

实验平台：自主研发的下肢康复机器人物理样机(图5)[14]，该系统主要由机械本体和电气控制柜组成。

图5 下肢康复机器人实验系统

3.1 轨迹跟踪实验验证

将求解的圆周步态和类圆周步态关节角度数据输入上位机，控制机器人运动，采集关节电机编码器反馈的脉冲，转化为对应的角度。

采集的不同ratio下两个周期的关节角度变化曲线与理论值的对比见图6，表1 为两个关节在不同ratio下的位置跟踪误差最大值。

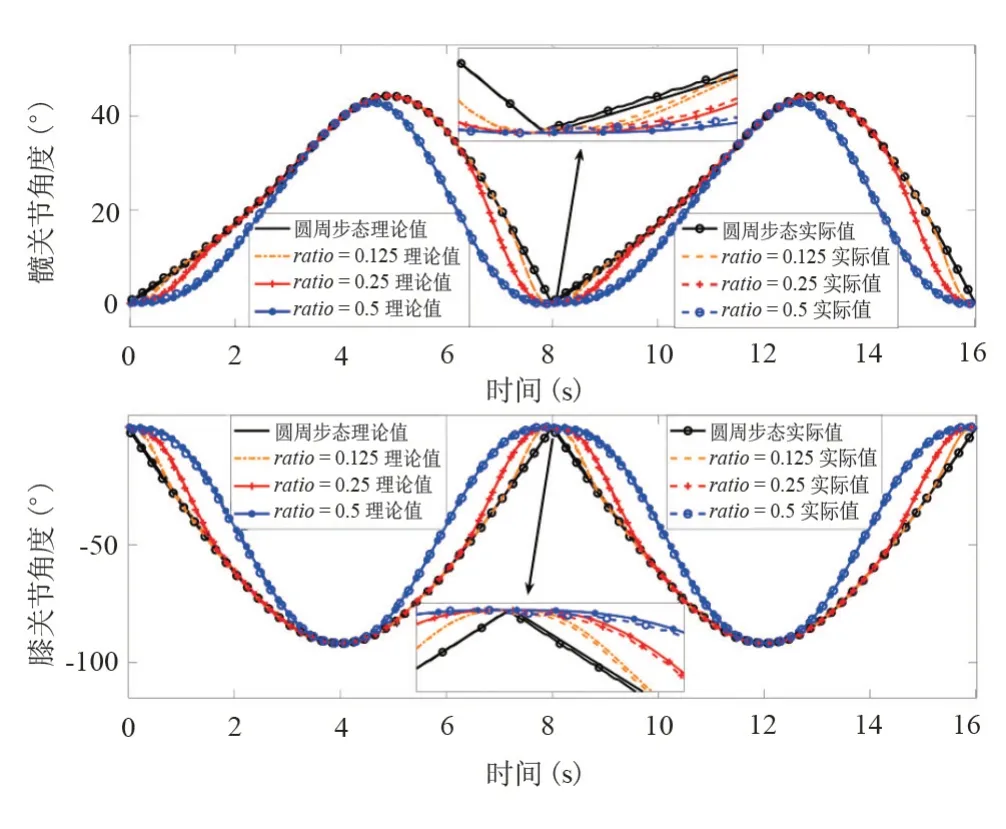
图6 圆周和类圆周步态的理论与实际关节角度

由表1 可知下肢康复机器人在运动时存在跟踪误差，其中膝关节负向误差较大，但是其正向误差较小，在训练时不会因此对患者造成伤害，而髋关节的误差绝对值小于0.6°，满足患者的康复训练需求。

表1 圆周步态和类圆周步态两个周期关节轨迹最大跟踪误差

3.2 末端轨迹、速度及加速度验证

将采集到的关节角度，通过一阶微分公式得到角速度，使用均值滤波进行去噪处理，可以得到3 种ratio下的类圆周步态连续两周期的速度变化(图7)，其结果与仿真(图3)基本吻合：康复训练过程中周期起点和终点时速度都为0，周期衔接处角速度变化连续。

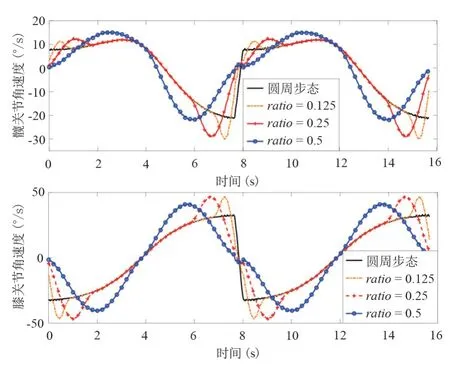
图7 圆周和类圆周步态实际角速度

使用二阶微分公式和低通滤波器滤波得到髋关节和膝关节的3 种ratio下两个周期的角加速度曲线(图8)，很明显圆周步态在周期衔接时存在角加速度突变，而且峰值明显高于3 种ratio下类圆周步态的角加速度峰值。随着ratio增大，类圆周步态角加速度变化更加平滑。根据髋关节、膝关节的角度，正运动学求解得到圆周步态以及类圆周步态的末端轨迹(图9)。可知ratio越小，类圆周步态末端轨迹与圆周步类似，随着ratio变大，末端轨迹完全不同于圆周步态。

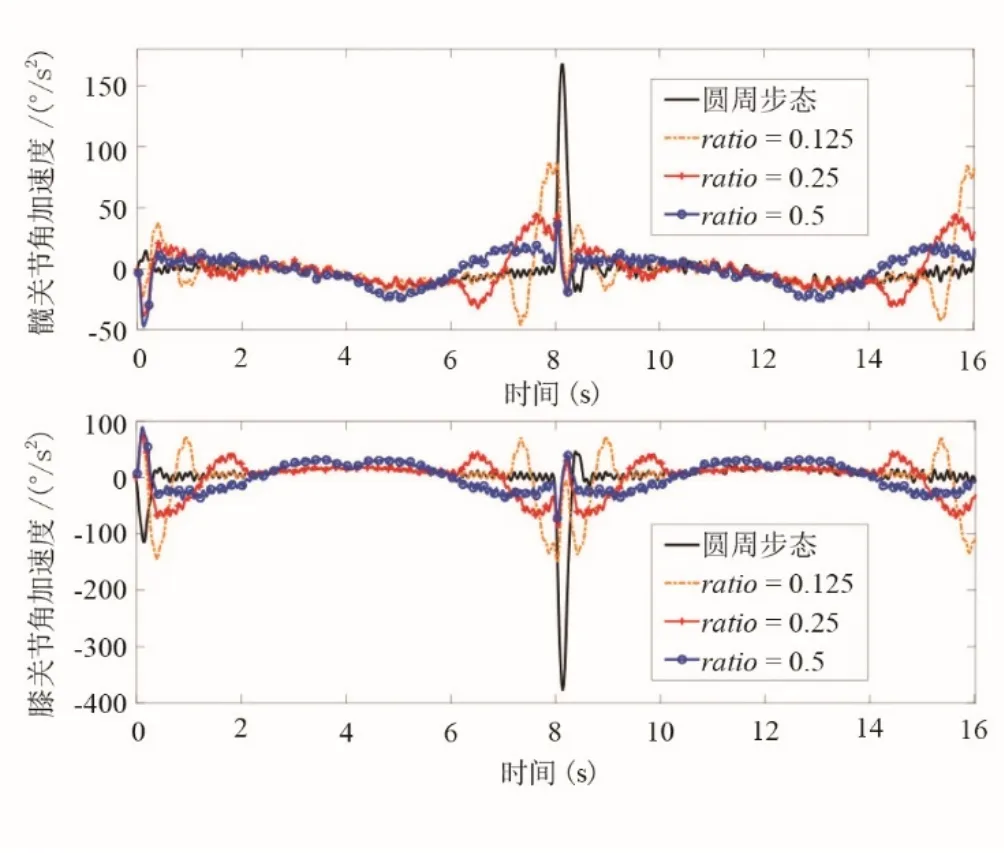
图8 连续2个周期的圆周和类圆周步态实际角加速度

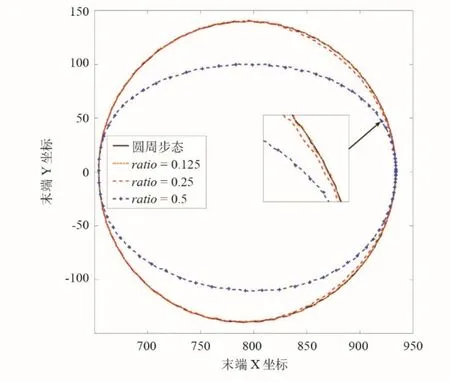
图9 圆周步态和类圆周步态单周期实际末端轨迹曲线

4 结论

本研究针对用于急性期患者被动训练的自主研发的下肢康复机器人，提出一种用于下肢康复的可变类圆周步态。该类圆周步态分为起始段、中间段和结束段三段规划，在起始段和结束段采用五次多项式进行规划，中间段保留圆周轨迹，保证下肢康复机器人末端轨迹与关节轨迹连续平滑。引入参数ratio确定轨迹分段区间的大小，因ratio取值不同获得不同步态轨迹，ratio越小，末端轨迹与圆周步态轨迹越相似。仿真及实验结果表明所提出的不同ratio下的类圆周步态规划均能够实现连续2 个运动周期衔接处角加速度平滑，下肢康复机器人运行平稳，验证了该方法的有效性，其康复疗效将在接下来的临床试验中进行验证。后续将进行仿人生理步态研究，满足患者中后期恢复行走能力需求。此外，步态轨迹算法未考虑到踝关节的活动度，后续工作将对此展开研究。

利益冲突声明：所有作者声明不存在利益冲突。