半潜式平台横向开闭极限强度的时变可靠性分析
钱呈龙 赵 南 王 璞 李钧晖 吴剑国
(1.浙江工业大学 土木工程学院 杭州310023;2.中国船舶科学研究中心 无锡214082;3.中国船舶及海洋工程设计研究院 上海200011)
引 言
半潜式平台在使用期间由于风浪和海水的作用,必然会受到疲劳和腐蚀的影响,而这些疲劳裂纹扩展以及构件厚度降低会导致平台结构极限强度减小,使平台的可靠性随时间而降低。现今对于船体在疲劳和腐蚀作用下的时变可靠性研究工作较多,例如:刘益清[1]分析计算了船体在疲劳和腐蚀损伤下的可靠性;施兴华[2]使用上穿率法,对舰船结构的时变可靠性进行了分析计算。
然而,针对半潜式平台结构时变可靠性的研究工作相对较少。考虑到随机变化的腐蚀和疲劳裂纹影响,本文将半潜式平台结构横向开/闭的极限强度视为一个随机过程,采用上穿率法[3]进行分析,通过并联系统的方法来计算其时变可靠性,并且与瞬时可靠性作对比分析。
1 半潜式平台的极限强度时变模型
1.1 疲劳裂纹影响模型
平台结构构件有效宽度减小主要是由裂纹扩展导致,进而使得结构的极限强度降低。在疲劳分析中,一般引入有裂纹存在的初始条件,在此基础上,采用Paris-Erdogan方程[4]来建立疲劳裂纹扩展模型:

1.2 腐蚀影响模型
腐蚀作用会使平台结构构件的厚度减小,导致结构极限强度降低,本文采用一般的腐蚀模型[6]:
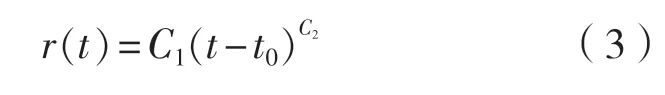
式中, 为t时间内受腐蚀的厚度,mm;C1为年腐蚀率[5],mm/a;C2的取值范围是1/3~1,本文取值C2= 1.0; t0为防腐涂料的寿命,a。
1.3 半潜式平台结构极限强度
半潜式平台在计算横向闭合极限承载力时主要考虑的是整体失稳,而在计算横向闭合极限承载力时的整体失稳主要体现在底部横撑的整体受压屈曲破坏。传统的Smith法没有考虑到这一点,因此需要对Smith法作出改进,使之在对半潜式平台横向闭合工况极限承载力计算时,考虑底部横撑的整体受压。
基于Smith法的基本假定[6],将半潜式平台横剖面离散成普通扶强材、硬角、加筋板3类结构单元,以及横撑单元。硬角单元在拉伸和压缩的状态下,其破坏模式均为弹—塑性屈服破坏;扶强材单元在受拉时是弹—塑性屈服失效破坏,受压时有梁柱屈曲、扭转屈曲以及腹板局部屈曲等多种失效模式;加筋板格单元拉伸时表现为屈服失效,受压时则为板材屈曲。横撑的局部稳定按照船体规范的Smith法单元划分,应力应变关系也按照规范。整体稳定的应力应变关系如下:
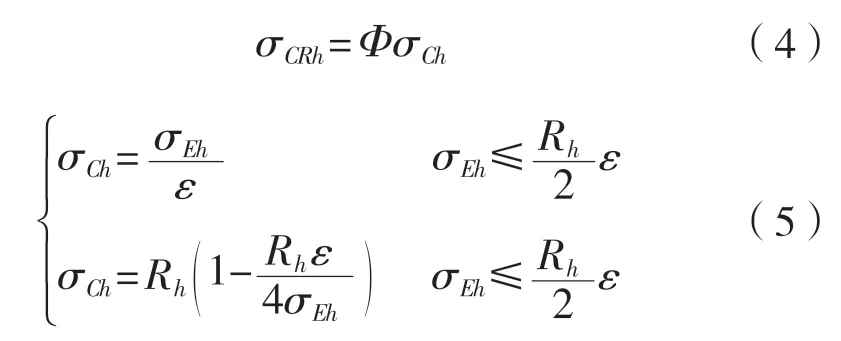
式中:Φ为边缘函数, 为横撑的临界应力,MPa;
为横撑的欧拉力,MPa;Ah为横撑截面面积,mm2。
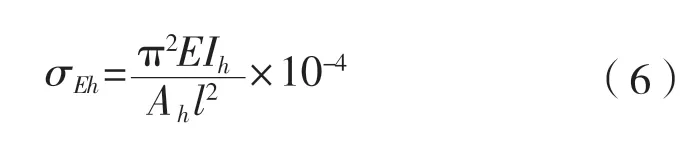
式中:Ih为横撑惯性矩,mm4;Rh为横撑屈服强度,MPa; ε为相对应变;l为横撑长度,mm。
改进后的Smith法计算步骤是:
(1)将半潜式平台横剖面离散成普通扶强材、硬角、加筋板和横撑4类结构单元,其中前3种单元见CCS规范[7],横撑单元专门针对平台的横撑,将其简化为两端铰接,轴心受力的薄壁受压杆件,考虑其整体稳定性。
(2)确定单元的平均应力—应变曲线。
(3)计算得到平台的弹性中和轴位置,设初始步的曲率增量为χ1;。
(4)每个单元的应变εi都是根据平面假设计算所得,由平均应力-应变关系计算各单元应力σi。
(5)计算横撑单元的应变εi,根据应力-应变关系计算横撑所属单元的应力σi。
(6)由横剖面的力的平衡来确定下一增量步的截面中和轴位置。
(7)通过合计所有单元的贡献计算相应弯矩Mi。
(8)与前一增量步的弯矩比较Mi-1。若Mi-1<Mi,则终止计算并定义弯矩极值;否则,以递增方式增加曲率Δχ并继续执行步骤4。
与传统Smith法相比,主要是增加第(5)步关于横撑单元应力计算,修改Smith法第(8)步。
1.4 受疲劳和腐蚀影响的半潜式平台极限强度时变模型
平台的极限强度随着疲劳裂纹的扩展以及腐蚀的加重会逐年下降,对于扶强材和加筋板单元,由于腐蚀作用厚度随着时间的增长而减小,其宽度由于疲劳裂纹的扩展而降低,即可得:
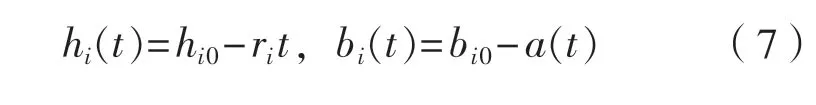
式中:hi0、bi0为扶强材(加筋板)的初始厚度和宽度,mm;ri为扶强材(加筋板)的腐蚀率,mm/a。
对于硬角和横撑单元,主要受腐蚀作用影响,厚度随着时间的增长而减小,可得:

在计算可靠性的时候,由文献[8]可认为平台结构极限强度服从对数正态分布,其均值函数和标准差函数由影响极限强度的不确定因素通过Rosenbluth法[9]求得,并且能得出,他们都是关于时间的函数,因此平台极限强度应该用随机过程模型来描述。
2 半潜式平台的载荷
2.1 静水弯矩
半潜式平台的横向静水弯矩主要由静水浮力与重力共同作用产生。参考小水面线船[10],所受总体静水弯矩,其 由公式计算得:
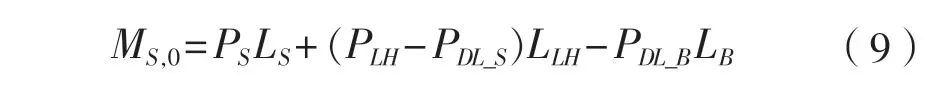
式中:PS为支柱浮力,N;LS为PS至中纵剖面的水平距离,m;PLH为下浮体浮力,N;LLH为PLH至中纵剖面的水平距离,m;PDL_S为支柱与下浮体重量,N;PDL_B为上部结构的重力载荷,N。
2.2 波浪弯矩
波浪弯矩具有长期的不稳定性,主要来源有海况发生概率、波浪谱型、有义波高和载荷传递函数等,它的长期预报是基于海浪短期预报,通常将波浪弯矩模型化为Poisson过程[11],海洋结构使用期内波浪弯矩极值的累积概率分布函数可表示为:

式中:为波浪弯矩的平均达到率; 为平台使用期限T0内出现的最大波浪弯矩,N·m。
2.3 载荷组合
半潜式平台总弯矩由静水弯矩和波浪弯矩组成,传统的分析方法是将两者线性相加,但在实际当中,它们一般不会同时以其最大值出现,本文考虑了载荷的组合问题,此时总弯矩表示为:
式中:为载荷折减系数,详见参考文献[12]。
3 可靠性计算
半潜式平台横向开/闭极限强度的时变可靠性状态方程为:


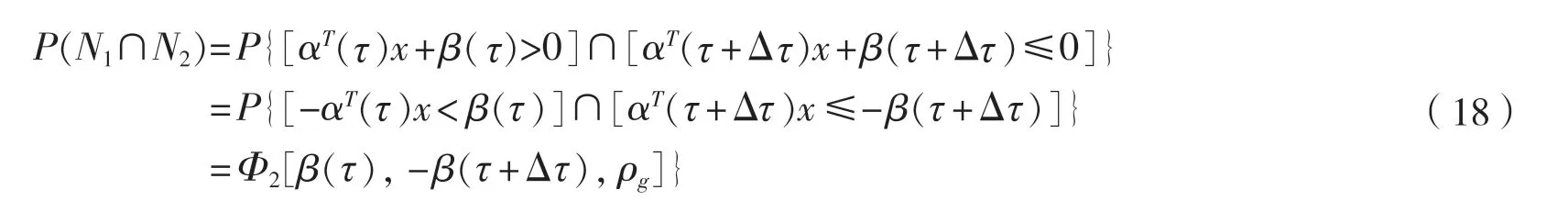

4 实例计算
4.1 平台主尺度
半潜式平台主尺寸见表1。
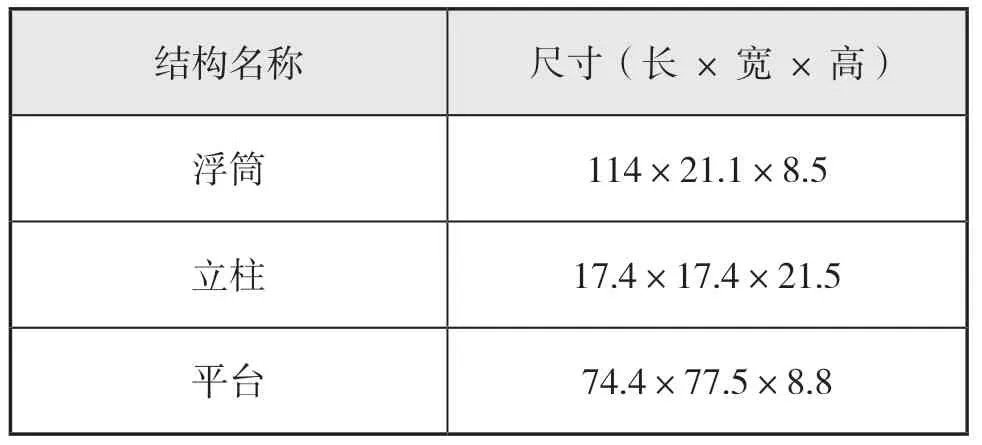
表1 半潜式平台的主尺度m
4.2 极限强度分析
改进后的Smith法考虑了横撑结构受压时会发生整体失稳的情况,能够更准确地模拟存在横撑整体失稳模型的弯曲极限承载力,采用VB自编程序,对半潜式平台在横向开闭工况下的极限弯矩进行计算,并将所得结果与平台细化模型的有限元数值模拟结果相比较,在还未考虑疲劳和腐蚀影响下的初始时刻,不同工况下有限元与Smith 法的结果见下页表2和图1、图2。
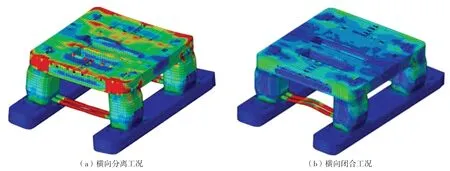
图1 半潜平台模型横向开闭工况极限状态示意图
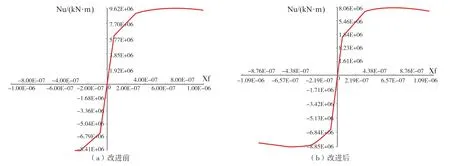
图2 Smith法不同工况下的弯矩转角曲线图

表2 半潜平台模型在不同工况下极限承载力汇总MN
在横向闭合工况下,改进前后结果相差30%左右,这是因为此时横撑受压发生整体失稳。在横向分离工况下,改进前后结果仅相差1%,此时横撑受拉,这说明改进后Smith法结果准确。而在横向闭合工况下,有限元模型结果与改进后结果相差4%,说明改进后 Smith 法能够更准确地模拟存在横撑整体失稳模型的弯曲极限承载力。
4.3 极限强度的概率特性
影响平台结构极限强度的随机变量概率特征见下页表3。
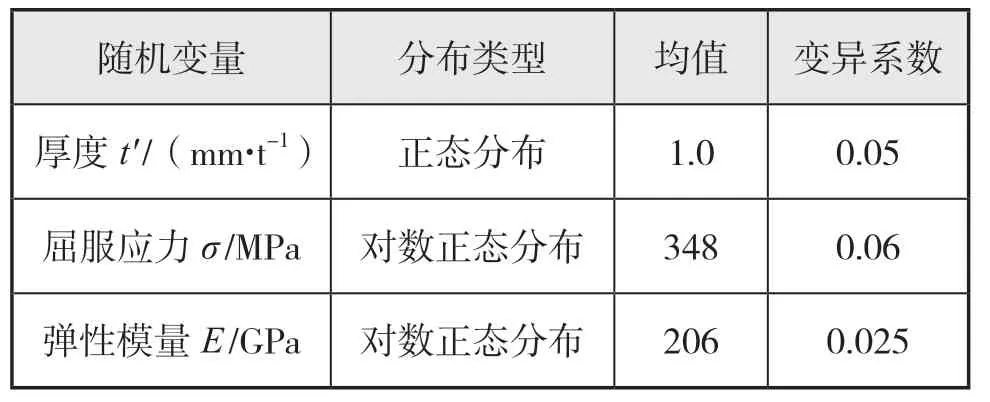
表3 随机变量概率特征
由参考文献[13],得到公式(1)中各参数,Δσ= 32.6 MPa,C= 1.07-11,a0= 0.5,Y= 1。公式(7)中,本文年腐蚀率C1取值0.1 mm/a。平台结构极限强度服从对数正态分布,在疲劳和腐蚀的影响下,使用自编程序对平台结构在使用期间的极限强度进行计算,得出均值随时间改变,并呈现为逐年递减的趋势,均值曲线见图3,而且变异系数也成递减趋势,但是相比于均值变化幅度很小。并且通过计算,当C1取值0.1 mm/a时,结构20年内损失为7.8%;C1取值0.2 mm/a时,结构20年内损失为11.4%;C1取值0.3 mm/a时,结构20年内损失为15.9%。可见,不同的年腐蚀率对极限强度影响较大,进而影响结构可靠度。
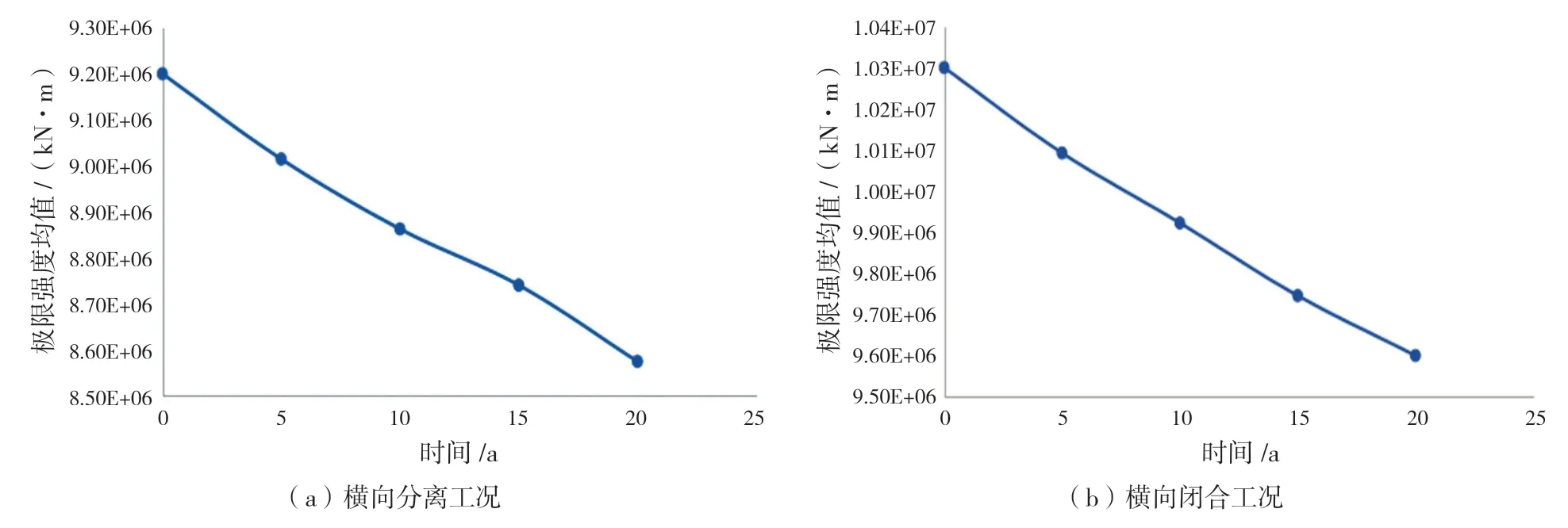
图3 不同工况下结构极限强度均值随时间变化曲线(C1 = 0.1 mm/a)
4.4 静水弯矩的概率特性
横向分离状态下静水弯矩任意运营时间T的均值由式(20)求得,标准差[2]由式(21)求得:
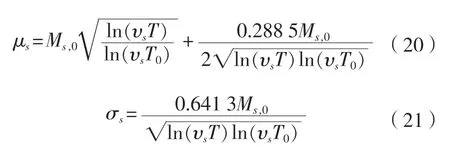
横向闭合状态下静水弯矩任意运营时间T的均值和标准差由式(22)和式(23)求得:
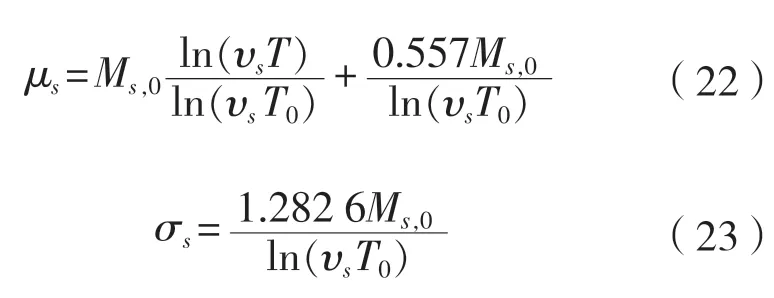
式中:为横向闭合与分离工况的平均发生概率[14],单位为1/d,文中取 =1/60; 平台的设计使用年限,在本文中取T0= 20 a。并且为更接近实际工程情况,在可靠性计算中将静水弯矩看作服从正态分布的随机变量,不随时间变化。
4.5 波浪弯矩的概率特性
通过公式(24)和公式(25)求得波浪弯矩在平台任意使用时间T的均值和标准差:
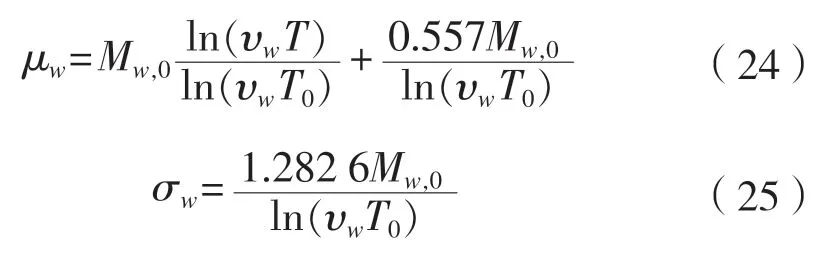
式中:为一次波浪循环的出现率,假设在平台使用期限内与海浪的遭遇次数为108次,即 =108。
按上所述,例如在平台使用初期(T= 1 a)时,各载荷的概率特征见表4。
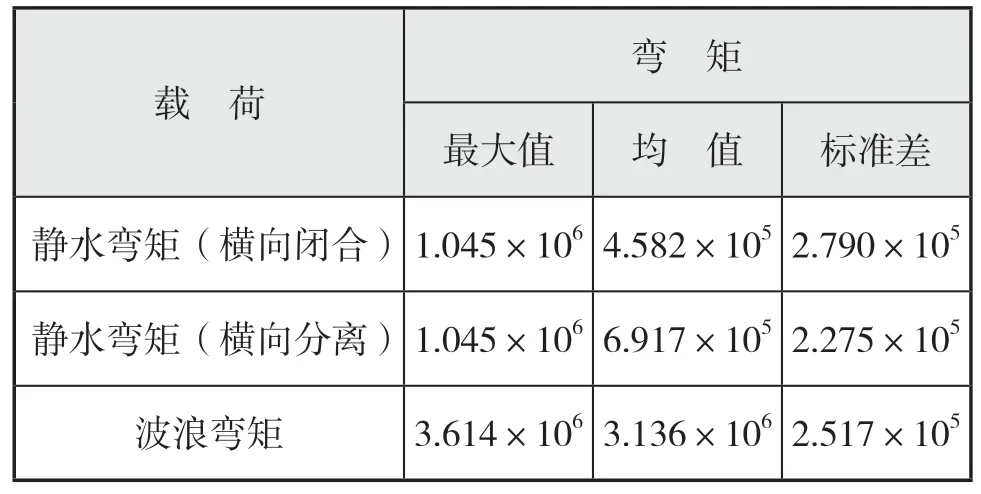
表4 T = 1a时各载荷的概率特征kN·m
4.6 时变可靠度分析
通过上述方法计算平台结构在疲劳和腐蚀作用下的时变可靠性,采用传统的JC法对相应的瞬时可靠性进行了计算,并对两者进行比对分析,考虑到半潜式平台在使用初期的结构强度很高,故假定其在t= 0时的失效概率为0。
图4的(a)和(b)分别表示年腐蚀率C1取0.1 mm/a时,横向分离与闭合工况下受疲劳和腐蚀影响的时变失效概率;图5的(a)和(b)分别为年腐蚀率C1取0.1 mm/a时,横向分离与闭合工况下平台结构可靠性指标的时变值和瞬时值。
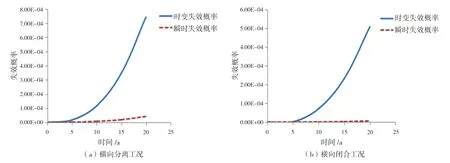
图4 横向开/闭极限强度的时变失效概率、瞬时失效概率(C1 = 0.1 mm/a)
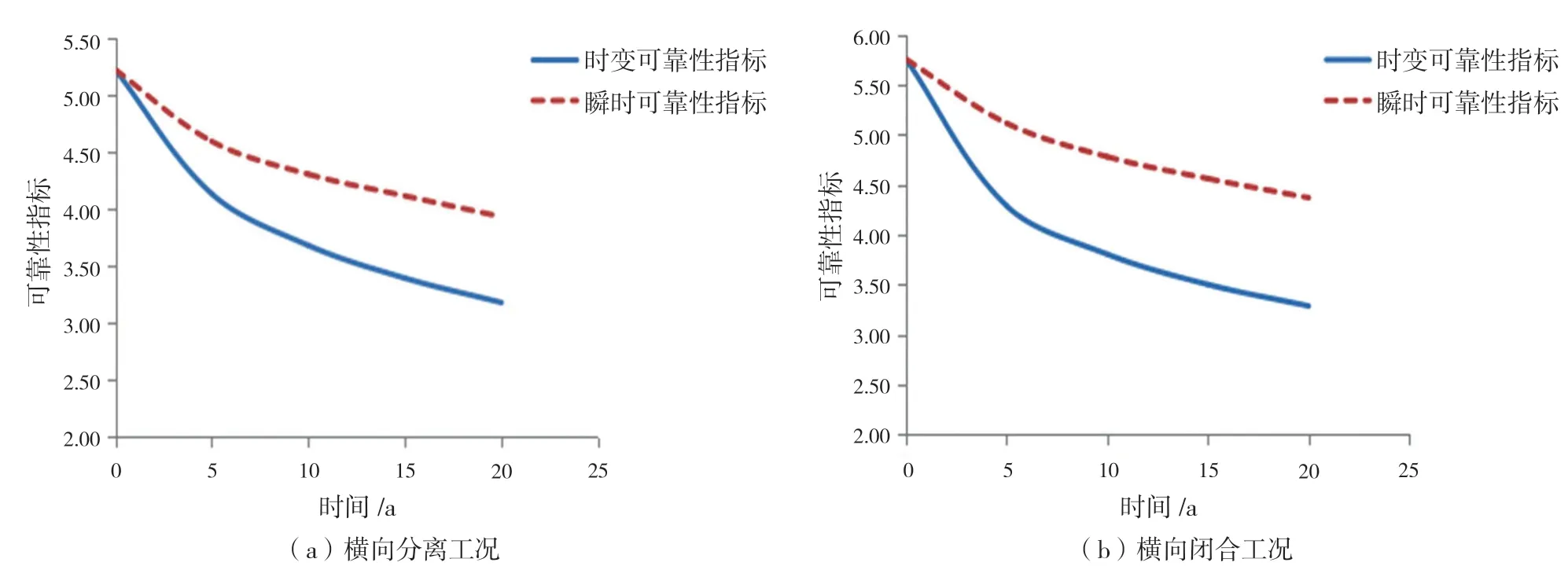
图5 横向开/闭极限强度的时变可靠指标、瞬时可靠指标(C1 = 0.1 mm/a)
由图4可知,在8年以前失效概率的时变值和瞬时值都较小,并且相差不大,这是因为初始疲劳裂纹和腐蚀相对较小,对结构强度几乎没有影响。但随着裂纹的继续扩展以及腐蚀的作用,从第10年到20年,时变失效概率已呈曲线增长,并且从第5年开始与瞬时失效概率相差较大,因为后者只是计算在t时刻的瞬间失效,并没有考虑这个时刻以前或以后的情况。
由图5可得,时变与瞬变的可靠指标曲线趋势一致,但是将结构极限强度视为随机过程后,由此得出的时变可靠度比相应的瞬时可靠度要更低。因此,从安全的角度出发,使用考虑疲劳与腐蚀作用的时变可靠性方法对平台结构进行评估更为合理。
针对可靠性结果影响较大的腐蚀率进行敏度分析,在上文年腐蚀率C1= 0.1 mm/a基础上,增加了在C1= 0.2 mm/a和C1= 0.3 mm/a时,横向闭合工况下的时变可靠性指标计算结果,并对三者进行对比分析见图6。
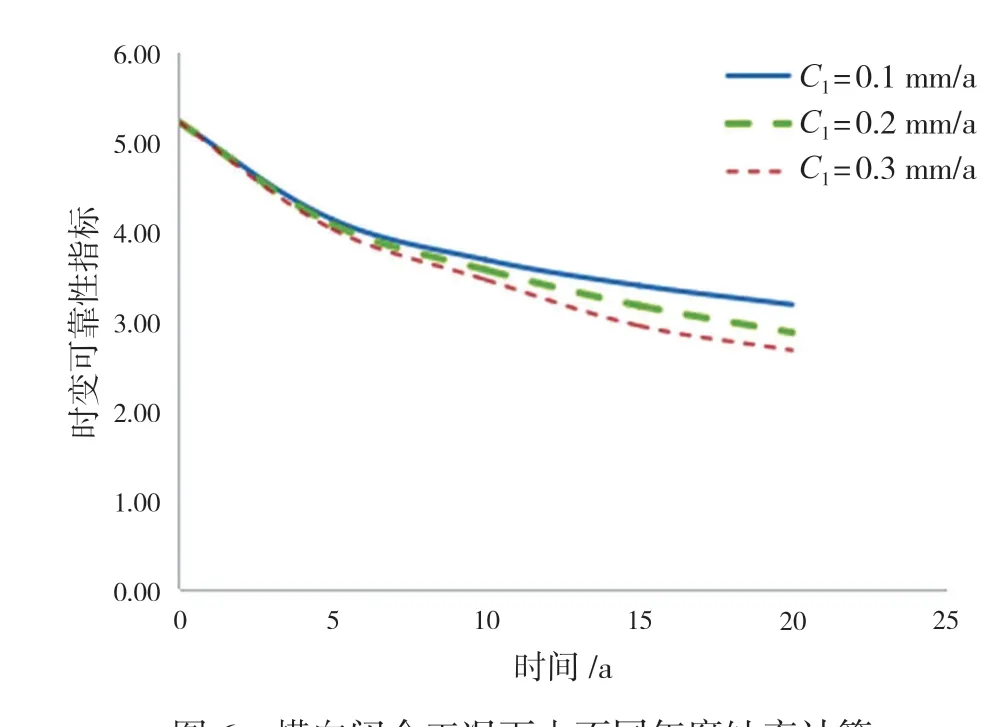
图6 横向闭合工况下由不同年腐蚀率计算所得时变可靠指标曲线
由图6可见,半潜式平台结构的时变可靠指标受腐蚀率的影响很大,且时间越长,影响程度越大,增加年检和阶段检验很有必要。
5 结 语
本文采用改进的Smith法来计算半潜式平台结构的极限强度,所得计算结果与ABAQUS软件计算结果相差很小。采用了符合半潜式平台自身材料属性和作业环境的疲劳和腐蚀参数,建立了考虑两者影响的半潜式平台横向开闭极限强度时变模型,并且引入随机过程,使得模型更为准确;使用上穿率法,将随机过程转化为随机变量,并通过传统的JC法来计算,方法简便且效率高。
由算例分析可以看出,该平台的横向开闭极限强度在10 a以前的时变可靠性变化不大,在10 a之后失效概率成抛物线增长,特别是在15 a之后,失效概率急剧增长。说明此时平台结构受腐蚀和疲劳裂纹扩展影响严重,故建议在15 a以后加强对平台结构安全评估和维护。

