用Tracker软件验证“皮带传动”和“齿轮传动”模型的规律

王春花 程敏熙

(华南师范大学物理与电信工程学院 广东 广州 510006)

要准确理解圆周运动,掌握线速度和角速度及它们之间的关系是关键.而圆周运动一节中“皮带传动”和“齿轮传动”两个模型的线速度、角速度及其比例关系的理解又是重难点.传统教学中,许多教师对待该部分只注重于理论讲解,甚至只要求学生记住结论.这容易使学生对圆周运动的理解模糊,对线速度、角速度的关系理解混乱.

基于此,并结合Tracker软件强大的追踪和数据处理功能,本文设计了一个可辅助教学的低成本、教师易操作、学生易理解的实验：用Tracker软件追踪“皮带传动”和“齿轮传动”两种模型下半径不同的各质点的运动轨迹,并通过软件同步显示质点的线速度、角速度,得到各质点线速度和角速度的定性和定量关系.有趣的实验,能激发学生学习的兴趣,也能辅助学生对内容的记忆和理解,有了准确的实验数据的支持,学生对结论也将更加信服,而不是带着疑惑的死记硬背.

1 实验原理

1.1 “皮带传动”和“齿轮传动”模型线速度和角速度的规律

1.1.1 线速度和角速度的大小关系

质点在相等时间内经过的弧长Δs相等,因此由

(1)

可得线速度v大小相等[1],即任意两质点满足

v1=v2

(2)

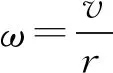
(3)

得半径r越大的质点角速度ω越小,且任意两质点角速度满足定量关系

(4)

1.1.2 线速度和角速度的方向关系

“皮带传动”和“齿轮传动”原理相似,角速度大小和线速度大小均满足上述关系.但二者又不完全相同,主要区别在于由同一皮带联系的质点转动方向一致,而由齿轮联系的质点转动方向相反.线速度因方向时刻变化，故只考虑大小,可只由角速度符号看转动方向,即“齿轮传动”的两质点的角速度应差一负号.

1.2 Tracker软件使用原理

Tracker软件可追踪各质点任意时刻所处位置,并可在建立坐标系确定原点后直接读各质点半径、线速度及角速度的大小,且软件默认逆时针转动为正方向,由角速度符号可看出质点转动方向.对数据进行分析就可得出两种模型下各质点运动的线速度和角速度的关系.

2 实验步骤

2.1 “皮带传动”实验

实验仪器：华为P10plus手机(用于拍摄)，手机支架，安装有Tracker软件的笔记本电脑，两个直径不等的传动轮，传送皮带，电动机(用于带动传动轮做匀速圆周运动)，带导线电池盒，长木板及固定零件，刻度尺(用于定标).

仪器组装及固定：将电动机、小轮、电池盒连接成闭合回路并固定于长木板,大轮也固定于木板适当位置,并用皮带将两轮连接起来,将刻度尺置于整个装置左边,手机及支架固定在适当位置.整个装置如图1所示.

图1 “皮带传动”装置示意图

视频拍摄及导入：给发动机通电,传动轮开始做匀速圆周运动,待整套装置稳定工作后,按下手机开始摄像按钮.拍摄完成后,将视频上传至电脑,打开Tracker软件,点击左上角“文件”导入视频.点击左上方“显示,隐藏或选择定标工具”进行标尺设定,将定标尺两端定位在刻度尺15 cm和20 cm处,输入长度5 cm完成定标[2].点击左上方“显示/隐藏坐标轴”进行建系,将坐标原点固定于小传动轮圆心.点击“创建”按钮选择创建质点[3],分别将大轮和小轮边缘处两质点创建为“质量A”和“质量B”(两质点均事先用黄色纸片标注).使用快捷键Shift+Ctrl同时单击要追踪的质点进行自动追踪[4],追踪到两质点轨迹如图2所示.

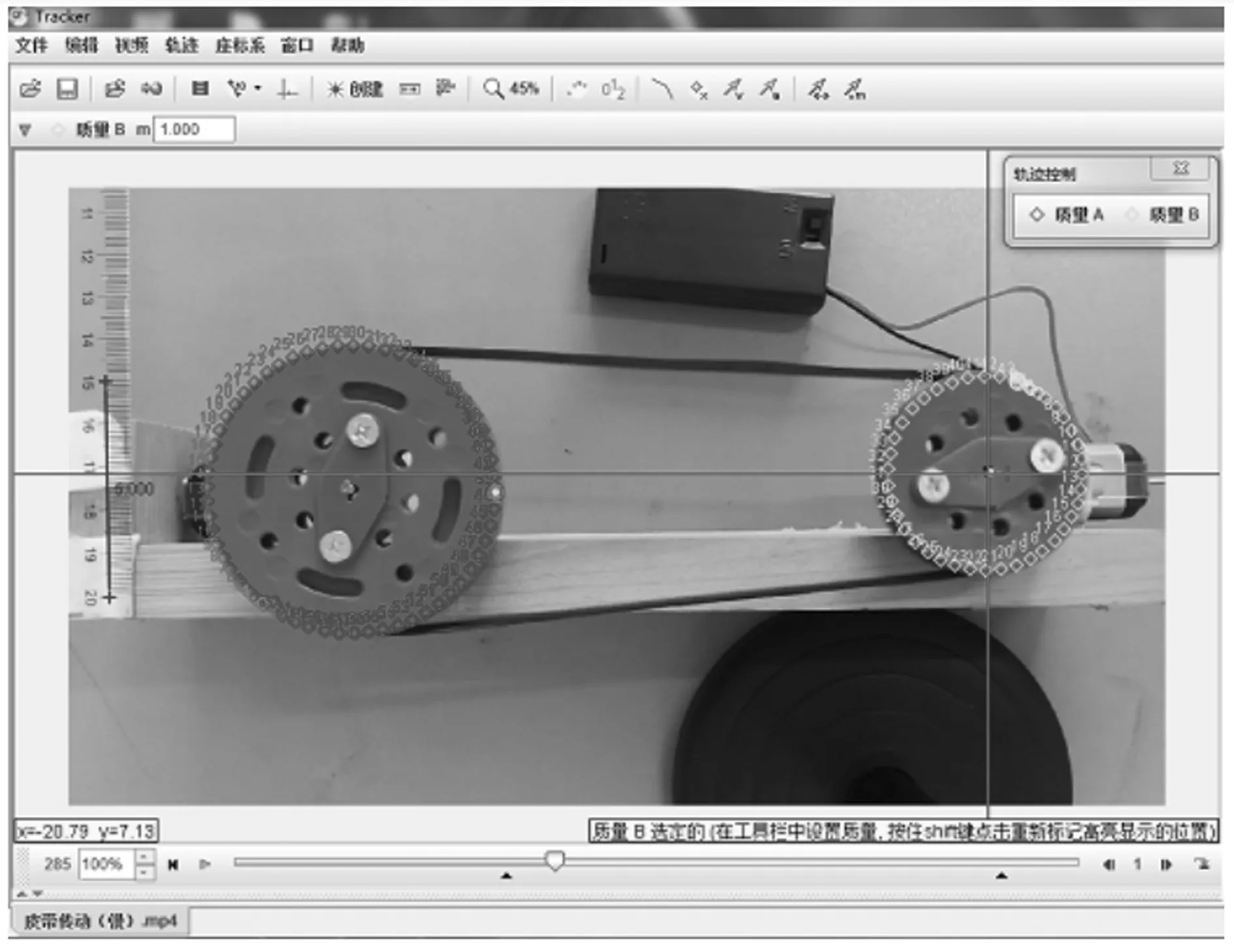
图2 “皮带传动”质点轨迹

2.2 “齿轮传动”实验

实验仪器：将“皮带传动”实验中两个直径不等的传动轮换成齿轮并取走传送带即可.

仪器组装及固定：将电动机、小齿轮、电池盒连接成闭合回路并固定于长木板,大齿轮固定于小齿轮附近并使两齿轮的齿啮合良好,将刻度尺置于整个装置左边,手机及支架固定在适当位置.整个装置如图3所示.

图3 “齿轮传动”装置示意图

视频拍摄及导入重复“皮带传动”实验操作,得到两质点轨迹如图4所示

图4 “齿轮传动”质点轨迹

2.3 数据输出与分析

将Tracker软件右下方数据输出界面设置为表格视图,选择要分析的质点,点击“表格”按钮勾选“r”“v”“ω”3个物理量,就能得到质点各时刻对应的半径r、线速度v和角速度ω.如表1数据以“皮带传动”的质点A为例.

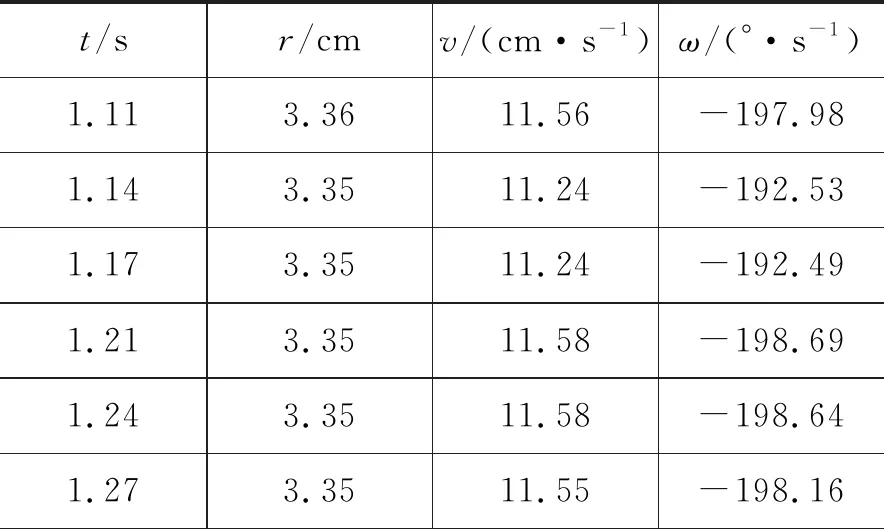
表1 质点A运动状态

续表1

质点B和“齿轮传动”的两质点重复质点A操作,但需注意分析不同传动轮或齿轮时应先将坐标系原点定位于相应的圆心.

3 实验验证

3.1 “皮带传动”模型线速度和角速度的规律验证

大轮并未与通电电动机连接,而是靠与小轮联系的传动皮带转动起来,故质点A和B为皮带传动的两质点.

将Tracker软件输出的数据求平均值得到质点A和质点B的线速度

vA=11.30 cm/s

vB=11.34 cm/s

两质点线速度偏差

质点A和质点B的半径

rA=3.35 cm

rB=2.29 cm

则

质点A和质点B的角速度

ωA=-193.80 °/s

ωB=-284.43 °/s

则

有

即验证了皮带传动的两质点线速度大小相等,角速度随着半径的增大而减小,角速度大小之比等于半径之比的倒数，且因两质点转动方向一致角速度符号相同.

3.2 “齿轮传动”模型线速度和角速度的规律验证

Tracker软件输出质点A和质点B的线速度

vA=9.64 cm/svB=9.56 cm/s

两质点线速度偏差

质点A和质点B的半径

rA=2.97 cm

rB=2.05 cm

则

质点A和质点B的角速度

ωA=186.36 °/s

ωB=-267.87 °/s

则在大小上

有

即验证了“齿轮传动”两质点线速度大小相等,角速度随着半径的增大而减小,角速度大小之比等于半径之比的倒数,且因两质点转动方向相反角速度差一负号.

4 结论

通过Tracker软件得到的实验结果与理论符合度高,显示出了利用该软件做物理实验精度高的优越性,加之其成本低、易于操作、现象直观的优点为改进中学物理实验教学提供了一条切实可行的方法.

另说明,Tracker软件测得的时间t、半径r、线速度v和角速度ω均默认保留4位小数,如“皮带传动”中质点A的线速度vA=11.302 5 cm/s,但考虑到习惯上的计时规则及毫米刻度尺的读数规则,所测物理量均只保留了两位小数.