基于复杂网络的车载自组网拓扑特性分析

周贝贝，周鹏

（湖北汽车工业学院 电气与信息工程学院，湖北 十堰442002）

车载自组网（vehicular ad hoc network，VANET）是以实现车辆间的正常通信为目的、由人工搭建的自组织网络［1］。为了实现对交通信息的有效管理和利用，将每辆汽车作为互联和通信的信息源接入到互联网中，每辆车都为1 个节点，车辆之间的通信关系为连边，在一定范围内的通信关系构成VANET。与传统的静态通信网络相比，VANET 具备节点多样性，连接多样性等复杂网络的特征，所以可用复杂网络理论对其网络特征进行研究。认识车载自组网的拓扑结构及其演化规律，从而研究影响VANET 信息传输能力的关键特性，是优化网络路由策略的理论基础［2］。

目前VANET 拓扑特性是学者们研究的热点。张丽丽通过上海市4000多辆出租车的GPS数据对VANET 网的一些参数进行统计分析，发现VANET网具有无标度特性，同时网络的局部和整体均具有较高的聚类特性［3］。高天智结合图论和复杂网络理论，得出城市轨道网络具有无标度及小世界特性的结论［4］。黄加增基于复杂网络理论，利用相关参数对城市公交网络进行了分析，得出城市公交网络具有无标度特性的结论［5］。Zheng 分析了VANET网络瞬时拓扑特性，发现VANET 网不具有无标度特性，而当通信半径足够大时，显示出小世界特性［6］。Zhang 对城市环境下VANET 的动态拓扑特性进行了分析，发现通信半径是影响网络连通性的主要参数［7］。

网络拓扑结构与网络通信协议的设计密切相关。韦世红提出了一种基于小世界网络模型的层次型路由算法［8］，熊云艳基于度序列构造了复杂网络模型，并在此基础上对3种路由策略进行了分析对比［9］，基于网络拓扑结构和节点队列长度，Ling提出了新的全局动态路由［10］。虽然VANET网拓扑特性分析及通信协议的研究取得了不少成果，但仍然存在一些亟需解决的难题，比如VANET 是否具有无标度与小世界特性，在什么条件下会具有这些特性。在现有的文献资料中，关于这个问题的结论并不一致,甚至得出的结论截然相反。

当VANET 具有无标度特性时，在双对数坐标下，其度分布的概率密度函数为一条直线，为检验网络是否具有无标度特性提供了经验的检验方法。目前在对网络无标度特性的验证问题上，许多文献采用最小二乘法在双对数坐标下对网络的度分布进行直线拟合，从而计算缩放参数，但是使用这种方法时往往会产生较大系统误差［11-12］。主要原因在于，幂律分布属于肥尾分布，度分布的尾部取值较多且分散，此时采用标准线性回归方法对度分布进行拟合，会得到几种不同的解，并且这些解往往较真实参数偏低。Clauset 等曾将参数γ的极大似然估计和基于线性回归的最小二乘估计作比较，发现极大似然估计远比最小二乘估计精确［12］。实际应用中，最小二乘法在双对数坐标下度分布尾部拟合为直线可作为判定幂律分布的必要条件，需采用KS 检验和极大似然估计法对VANET 是否具有无标度特性进一步验证。

文中基于成都滴滴实际数据集和实验仿真数据集，分析了城市环境下VANET的拓扑特性，揭示了网络演化的规律。

1 VANET拓扑特性分析

城市环境下由车辆之间的通信关系组成的自组织网络是典型的复杂网络，可以借鉴复杂网络理论度分布、平均路径长度、聚类系数和连通分支数。对其进行分析。在刻画复杂网络结构的统计特性时，通常使用度分布、平均路径长度、聚类系数和连通分支数对其进行描述。

1.1 度分布

网络中度为x的节点与网络中节点总数目的比值即节点的度分布，常用分布函数P（x）来描述［13］，即

式中：N为网络中节点的总数；n（x）为度为x的节点数。无标度网络的显著特点是其节点度服从幂律分布，因此度分布可近似表示为幂函数：

式中：γ为缩放参数，取值2～3。节点连接度没有明显特征长度的网络，称为无标度网络，在这类网络中，大部分节点的度相对较低，少量节点的度相对较高，因此又称为非均匀网络，而具有相对很高度的节点称为网络的“枢纽”［14］。因此可通过判断网络的度分布函数是否符合幂律形式、缩放参数是否位于2～3来判定网络是否具有无标度特性。

文中采用KS检验和极大似然估计来进行缩放参数的计算。KS统计量即数据的分布函数与拟合模型之间的最大距离［12］：

式中：S（x）为落在区域x≥xmin上实际数据所对应的累积分布函数；P（x）为落在区域x≥xmin上实际数据所拟合的幂律分布函数；x为度值大小；xmin为幂律下界。使D值达到最小的点即xmin。离散幂律分布其缩放参数的极大似然估计表示为［12］

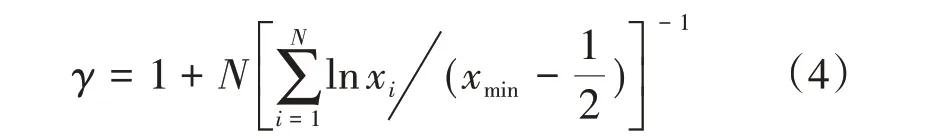
式中：xi为节点i的度值。

图1为指数分布在双对数坐标下的度分布图，可以看出，度分布的变化规律可用直线拟合，在最小二乘法中，网络度分布服从幂律分布。利用式（3）～（4）计算得γ为9.9，说明网络度分布不服从幂律分布，网络不具有无标度特性。因此在双对数坐标下，度分布尾部拟合为直线是判定幂律分布的必要条件，而不是充分条件。

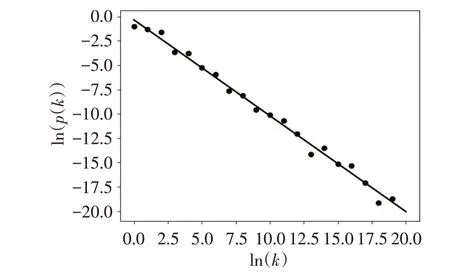
图1 指数分布y = e-x的对数拟合图

1.2 连通分支数

连通性对网络的通信具有至关重要的作用，当网络中出现分区或其他网络整体连通性被破坏的情形，网络中消息传递的整体覆盖性会被降低，从而极大影响其通信效率。通常情况下，网络连通性能的好坏可以通过连通分支的数目来反映。

1.3 聚类系数

网络的聚类系数是网络中局部聚集特征的反映。在VANET 中，聚类系数的数值往往和网络的密集程度以及局域连通性成正比，聚类系数对通信的可达性和整体网络的稳定性至关重要。将1 个节点的邻居节点之间实际存在的连边数与网络中可能存在的所有连边总数的比值定义为此节点的聚类系数［13］，即

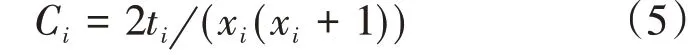
式中：Ci为节点i的聚类系数；xi为节点i的邻居节点的数量；ti为节点i的xi个邻居节点之间实际存在的连边数。

1.4 平均路径长度

平均路径长度为网络中任意两节点间距离的平均值［13］，即

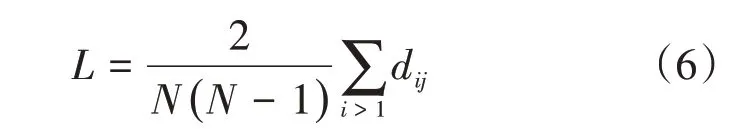
式中：N为网络中节点总数；dij为节点i、j之间的最短路径长度。当1 个网络同时具有较大聚类系数和较小平均路径长度时，称该网络具有小世界特性。平均路径长度是从全局角度描述网络中任意两节点间距离的特征参数，L越小车辆之间的通信越畅通，VANET 的可通达性越好。检查1 个网络是否为小世界网络，可以将L和平均聚类系数C与相同规模（具有相同的N和总边数K）的随机图的值Lrand和Crand进行比较，当L与Lrand为等阶量，C远大于Crand，即计算结果满足式（7）时，这个网络为小世界网络［14］。

式中：Lrand和Crand分别为相同规模的随机网络的平均路径长度和聚类系数。Lrand、Crand、网络平均度＜k＞、网络节点数N有如下关系：

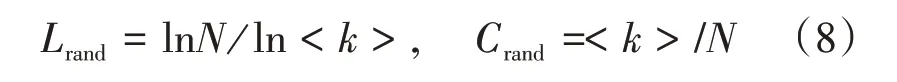
2 VANET拓扑特性实证研究

基于成都滴滴数据集GPS数据，首先根据经纬度和时刻的不同将数据集划分成小的数据集，具体划分情况见表1，然后利用复杂网络理论，对城市环境下VANET的拓扑特性进行实证研究。

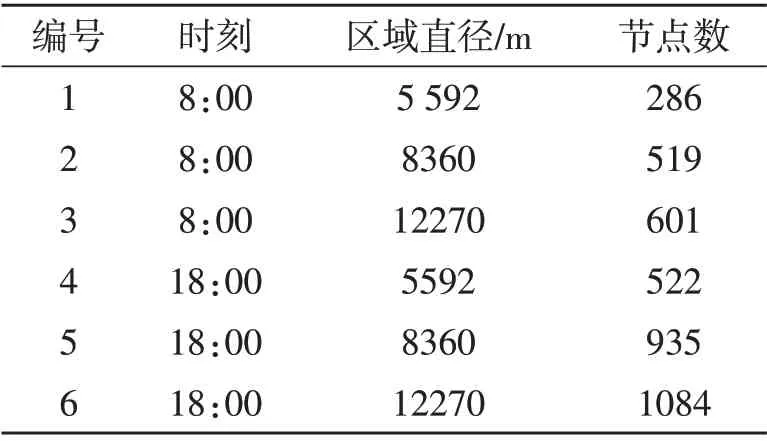
表1 实际数据集的划分

2.1 无标度特性分析

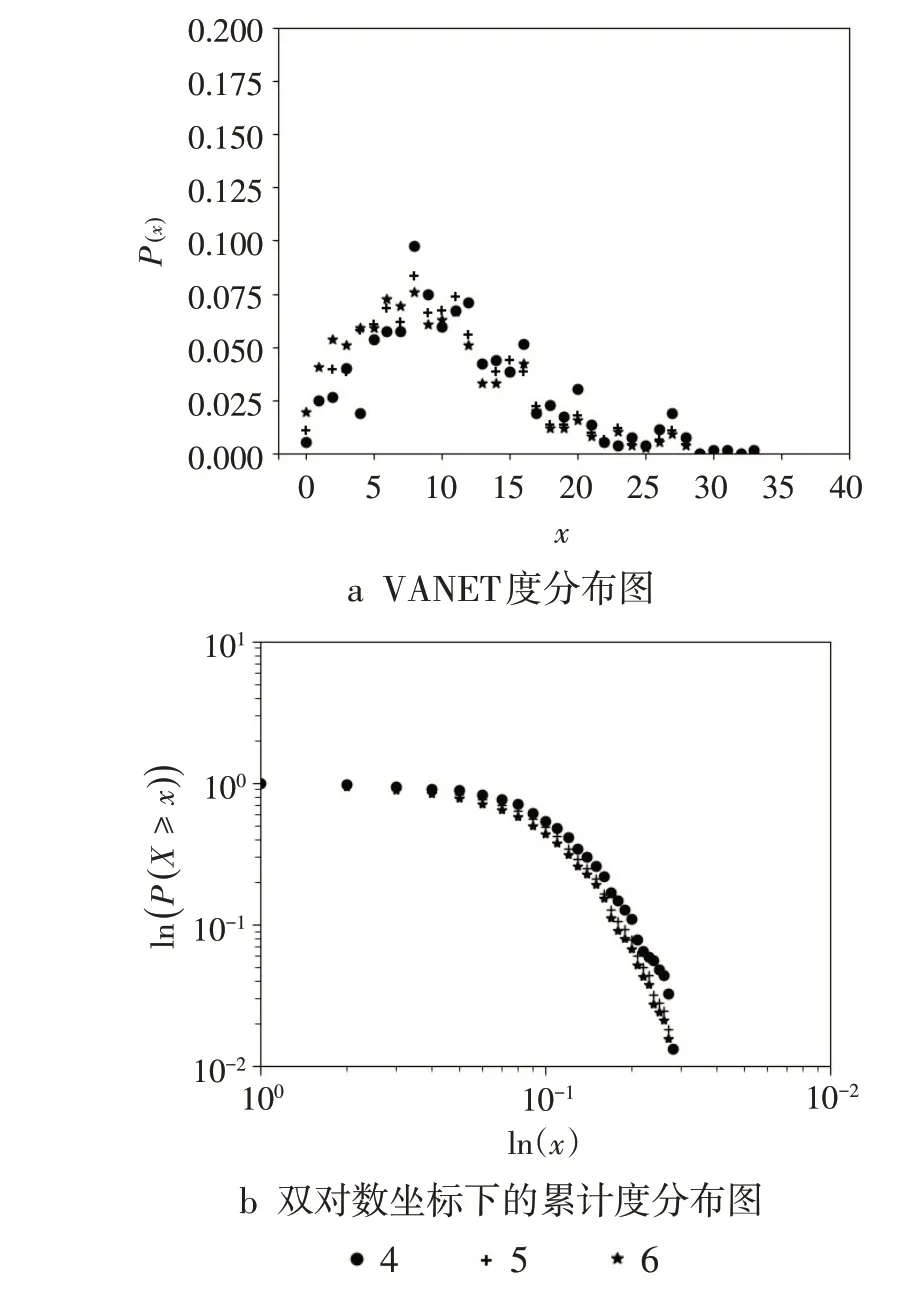
图2 R=300时实际数据集的度分布示意图

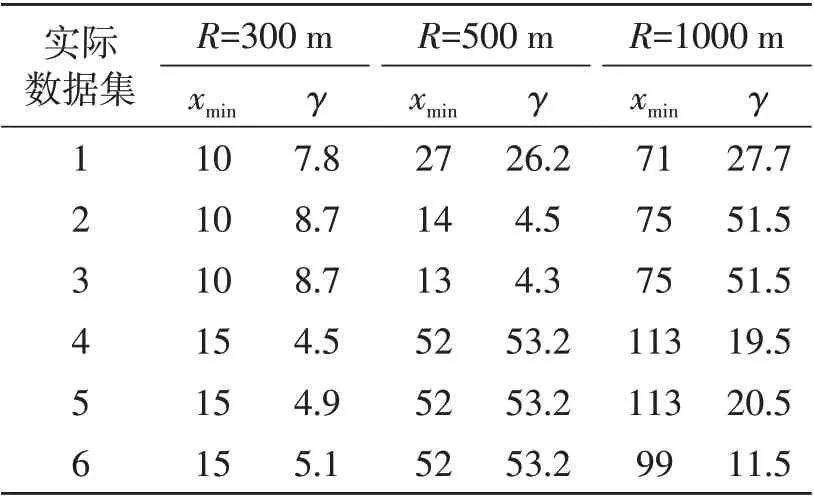
表2 实际数据集幂律参数

标度特性。为了验证结论的正确性，基于实际数据集中其他日期的GPS 数据也进行了度分布的γ计算，γ均大于3。由实验结果可以得到，在组网方式为通信半径范围内全连接，R从300 m增长到1000 m时，VANET不具有无标度特性。

为了进一步探究道路约束条件对VANET无标度特性的影响，在一定节点坐标范围内，随机取点生成了10 个仿真数据集文件，在相同的通信半径与组网方式下分析无道路约束条件下网络的无标度特性。仿真数据集中的节点数目在100～1000以每次增长100 个节点数递增，节点坐标范围为3000×3000，节点在区域内均匀分布。

图3a是仿真数据集6～10在R为300、连接方式为全连接时的度分布图，在双对数坐标下，由相应数据所组成网络的累计度分布如图3b 所示，其尾部分布近似于直线，符合无标度网络的度分布在双对数坐标下的变化趋势，但VANET 是否具有无标度特性还需进一步分析。由仿真数据集1～5 的GPS数据所组成的网络，在相同的半径和组网方式下，可得到与图3分布及走势类似的度分布图。

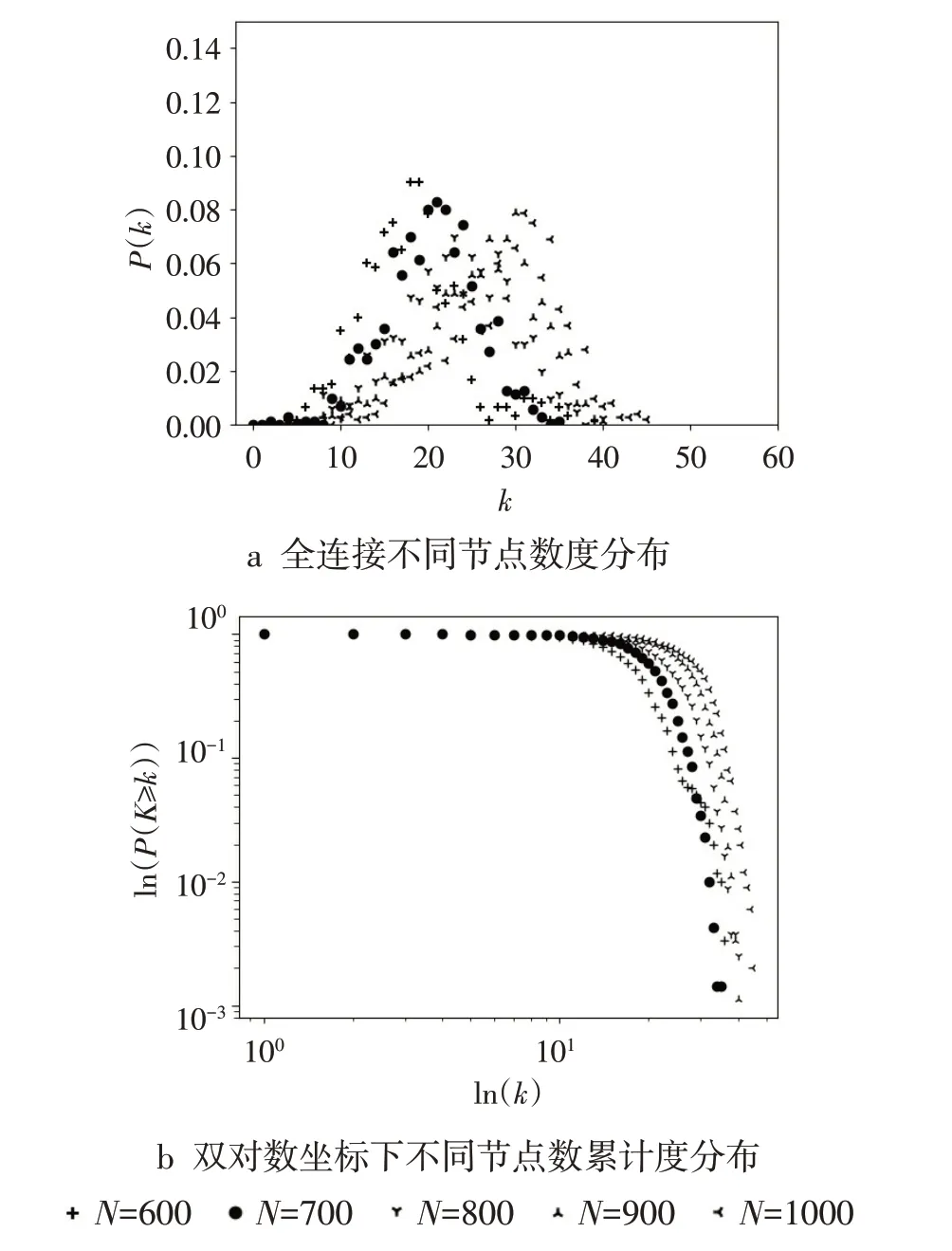
图3 R=300时仿真数据集的度分布示意图

采用与上述相同的方式计算幂律参数，如表3所示。从表3 可以看出，网络不具有无标度特性，说明无论是否具有道路约束条件，在全连接的组网方式下，VANET不具有无标度特性。

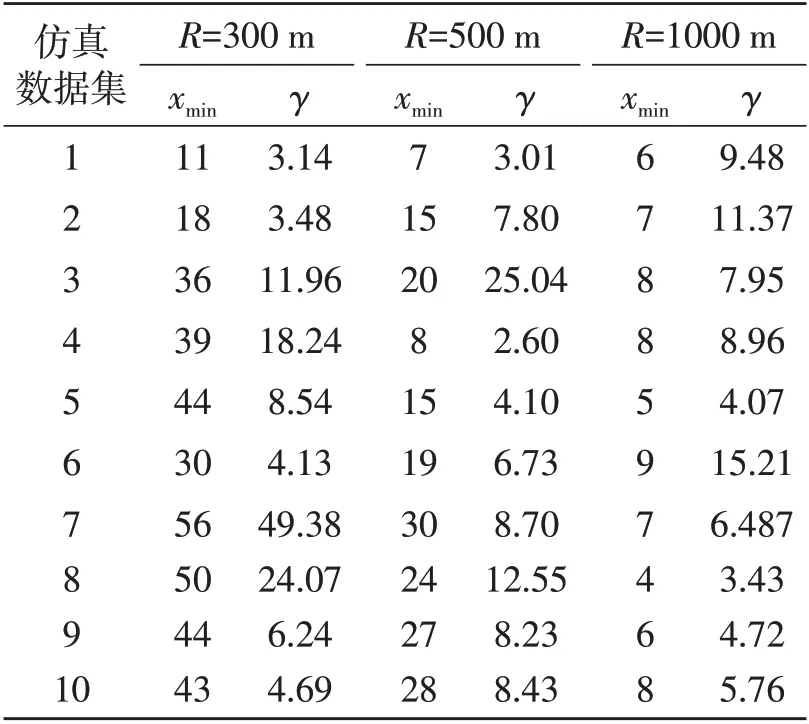
表3 仿真数据集幂律参数

2.2 连通性和小世界特性分析

从图4 可知，连通分支数随着R的增加而下降，当R达到400 m 时，连通分支数变化率下降速度显著加快，当R达到一定值后，连通分支数的下降速度逐渐平缓。由此可以通过分析连通分支数而选择适当的R。

图4 实际数据集连通分支数与通信半径之间的关系

图5为实际数据集1～6的VANET中，聚类系数随R变化的曲线，组网方式为通信半径范围内全连接。实际数据集1～3的R增加时，聚类系数略有波动，实际数据集4～6 的R增加时，聚类系数略有下降，但总体都维持在0.6左右，说明网络具有高聚类特性。取实际数据集其他日期的GPS 数据进行聚类系数的计算，计算结果虽然在数值上有一定差别，但总体维持在0.5左右。综上所述，在全连接组网方式下，R从300 m 增加到1000 m，VANET 的聚类系数总体维持在0.5左右，具有较高的聚类特性。

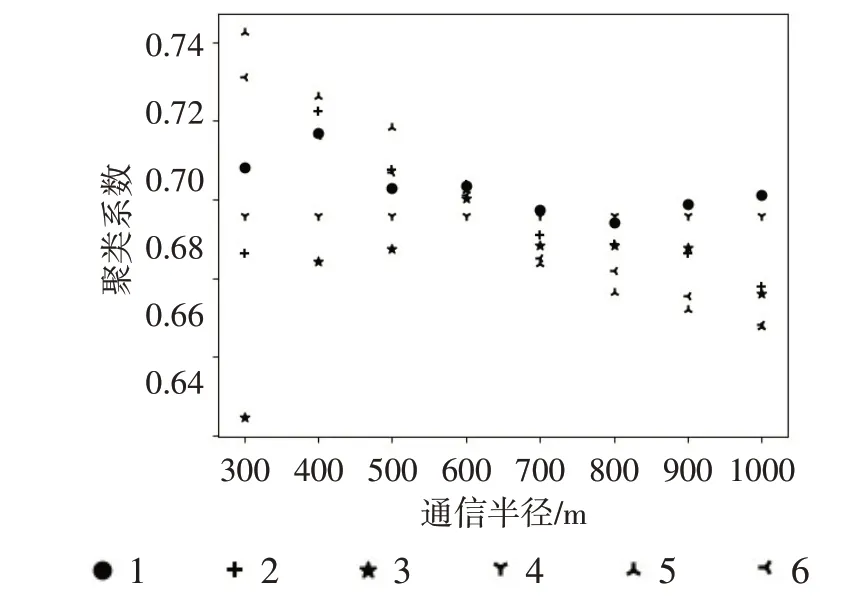
图5 实际数据集聚类系数与通信半径之间的关系

从图4 可以看出，实际数据集1 在R增长到600 m 时，连通分支数变为1，由不连通变为连通。实际数据集1 在组网方式为通信半径范围内全连接，R从600 m增长到1000 m时，运用networkx包计算网络的L、C、＜k＞，利用式（8）计算Lrand、Crand、L/Lrand和C/Crand。计算结果如表4 所示，L/Lrand均在2 左右，C/Crand远大于1，不完全满足式（7），所以在组网方式为通信半径范围内全连接，R从600 m 增长到1000 m时，VANET不具有小世界特性。

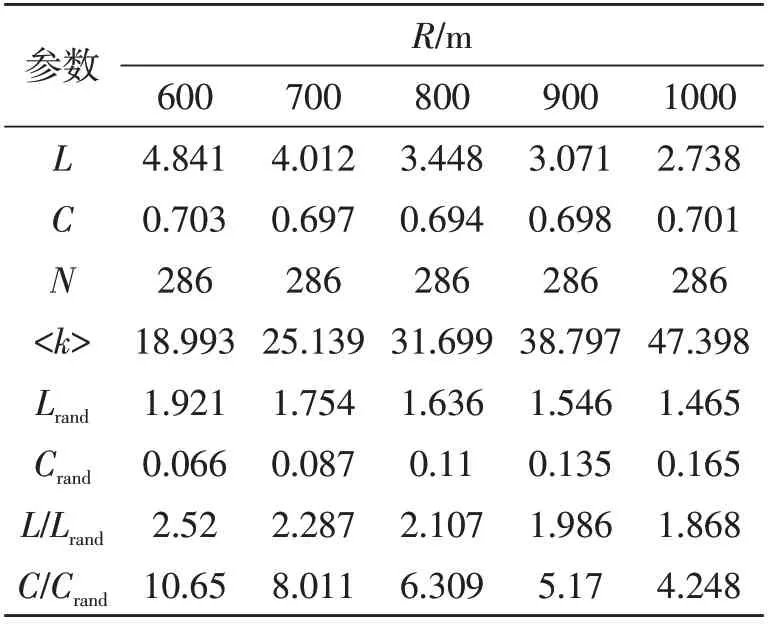
表4 不同通信半径下的小世界特性分析表

3 结论

基于复杂网络，以成都市滴滴数据集组成的VANET 为例，利用实际GPS数据分析了VANET 的基本拓扑特性。通过仿真验证得出，在通信半径内全连接的组网方式下，VANET 不具有无标度特性和小世界特性；网络整体具有高聚类特性；连通分支数随通信半径的增加而减少，当通信半径增加到一定值时，连通分支数变化率急速下降。结论为实际通信协议设计提供了支撑。例如在路由协议设计时，采用全连接方式得到的邻居节点不具有显著的度分布差异，因此节点度不适于用作选择下一跳路由节点的判据；在构造网络时，如果通过优先连接方式，可能会使得网络拓扑特征发生变化；如果网络具有无标度性，则可基于节点度数来设计路由协议。在优先连接方式下，网络具有何种拓扑特性，是后续要研究的内容。