基于支持向量机的电控发动机故障诊断

谢春丽，孙学志，高胜寒

（东北林业大学 交通学院，黑龙江 哈尔滨150040）

为了保证发动机安全、健康运行，其故障诊断及日常维护越来越受到重视，故障诊断方法的研究成为汽车行业的热门研究方向，例如文献［1］基于声强分析、不完全小波包分析和人工神经网络技术，提出基于噪声的发动机故障诊断WPA-ANN模型；文献［2］提出利用集合经验模态分解处理转速信号提取故障信息，该方法适合处理非平稳信号，并且有效解决了模态混叠的问题，具有较强的抗干扰能力；文献［3］介绍了BP神经网络及LM算法，利用改进的BP神经网络对发动机电控系统故障进行诊断研究。一般来说，故障诊断方法的研究主要分为2 种：1）从理论上对故障产生的机理进行分析，通过各性能参数之间的关系推导出故障方程；2）从统计学和机器学习的角度入手，是基于计算机大量数据学习的一种排除故障方法，使用计算机通过多种算法对正常数据或故障数据进行学习，得出性能参数之间内在的联系，然后建立预测模型用于故障诊断［4］。文中基于支持向量机（support vector machine，SVM）的电控发动机故障诊断方法，属于第2种研究方法，从机器学习角度入手，对采集到的电控发动机正常数据与故障数据进行小波包分解，并进行故障特征提取，结合振动信号的时域特征组成三维特征向量，建立SVM故障诊断模型进行训练，并利用该模型对电控发动机故障进行诊断。

1 振动信号分析与故障特征提取

发动机出现故障时，主要特征是机器伴有异常的振动和噪声，振动信号会出现非平稳、非线性等特征，敏感点振动参数往往有较为明显的变化，这种振动信号包含丰富的发动机状态信息［5］，可以用来获取发动机故障诊断信息。

1.1 振动信号的时域分析

分析信号在时域内的变化或分布称为时域分析，如信号的峰峰值PP、偏度S、峭度β和有效值Xrms等，部分时域参数的计算公式如下：

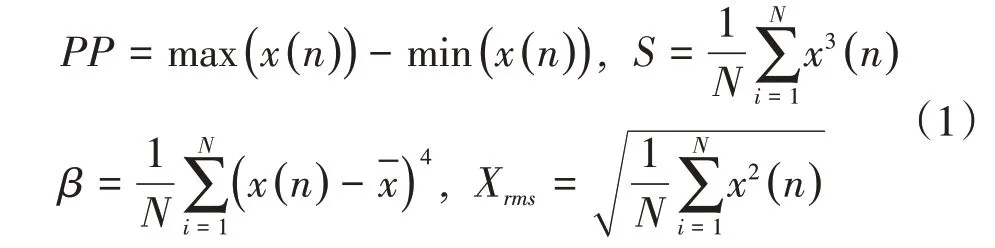
1.2 小波包变换

发动机故障时振动信号表现为非平稳的特征，若采用傅里叶分析，不能计算出具体时间节点的变化情况。小波包变换可以将不同频段上的信号按照不同的信号特征分离出来，再对分解后的信号分量处理，针对不同频段的信号特点提取特征量，来表征该分量信号的特征［6］。小波包算法的主要思想：首先对信号进行第1 次分解，形成信号的高频部分和低频部分；之后分别对高频和低频部分进行二抽一运算，将其偶数或者奇数部分保留，从而形成对高频和低频部分的分解，按照这种方式依次形成每层的信号分解，从而将信号分解到相邻的不同频段上［7］。小波包分解和重构公式为［8］

1.3 特征提取方法

画出第3层的能谱图，计算每层的能量比例［10］。小波能谱熵WEE计算公式为

将S和PP引入到信号特征提取中，与WEE一起建立三维特征向量［WEE，S，PP］，保证故障特征的全面性，同时减少由于数据因素导致的实验误差，提高预测的准确率。特征提取流程如图1所示。

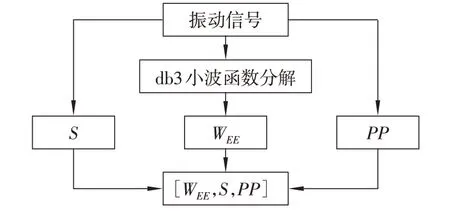
图1 特征提取流程图

2 SVM基本原理与模型建立

2.1 SVM概述

SVM是二分类模型，目的是寻找1个超平面对原样本进行分割，使间隔最大化，最终转化为二次规划问题求解［11］。最优分类面函数为

式中：αi为拉格朗日乘子，αi≥0。为了求式（6）的最小值，分别对ω、b、αi求偏导数，并令其等于0，求解最优分类面问题可以转变为凸二次规划寻优的对偶问题［13］：

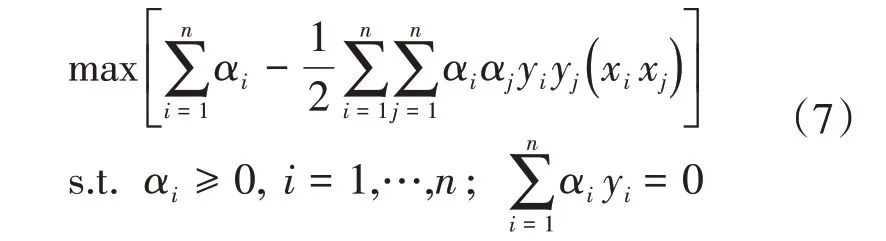
当在原始空间中的简单分类不能准确得到满意结果时，考虑将非线性问题转化为某个高维空间中的线性问题［14］，SVM通过核函数将n维矢量空间中的矢量x映射到高维空间，在高维空间中进行线性分类，分类函数变成

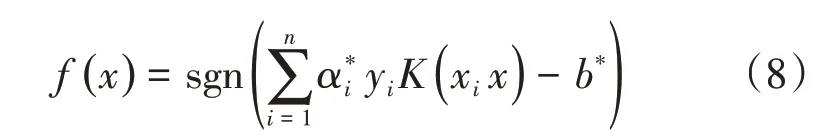
式中：sgn为符号函数；K(xi x)为核函数。文中选用径向基核函数：

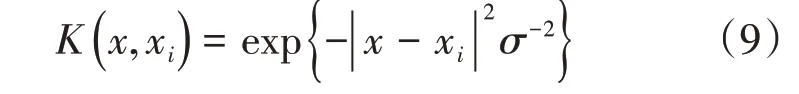
2.2 发动机故障诊断分类器设计

由于SVM 适合于二分类问题，文中包括无故障、其他故障、气缸故障，故建立SVM₀～SVM₄二分类器并级联，每个分类器都能将5种工况中的1种分离出来。分类示意图如图2所示。

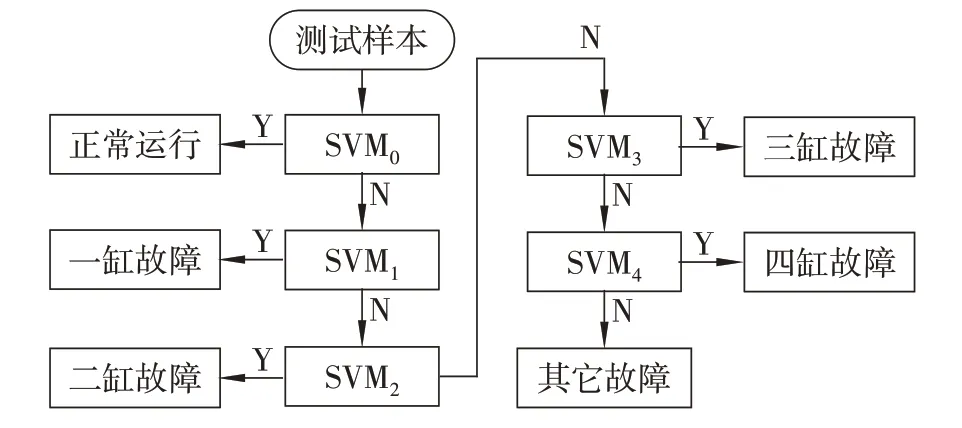
图2 故障分类器示意图

3 实验研究

3.1 实验原理、测试对象与实验设备

发动机发生故障时内部产生异常振动并传递到发动机外部，主要外部特征表现为发动机伴有异常的振动和噪音，振动激励源大都直接作用在缸盖上，汽缸盖上方异常振动尤为明显。压电式加速度传感器采集振动信号并将振动信号转变成电压信号，将转变的电压信号通过配套的电源适配器放大并利用数据采集卡采集数据，在数据采集卡的配套软件中将采集到的电信号再转换成数字信号进行保存［15］。对提取到的数字信号进行时域分析、小波包分解、小波包能谱熵分析，提取故障特征向量并输入到SVM 概率估计模型中，提供相应的针对各故障模式的后验概率分配，实现故障的定位。

文中选择哈飞赛马电控发动机DN4G15 为信息采集对象，主要参数如表1 所示，主要实验设备如表2 所示。利用测试设备采集电控发动机在正常运行、一缸故障、二缸故障、三缸故障、四缸故障工况下的振动信号，将其作为数据源。研究表明汽油机缸盖振动信号的分析频率不超过8 kHz，为了不遗漏有用的故障信息，将实验的釆样频率设为19 kHz，因此各釆样通道采样频率定为19 kHz，则信号分析频率为8 kHz［16］。

表1 目标车型主要技术参数

表2 主要实验设备

3.2 故障特征提取

1）振动信号时域图 利用压电式加速度传感器采集得到哈飞赛马电控发动机在怠速运转时不同工况下的振动信号，振动信号时域图如图3所示。

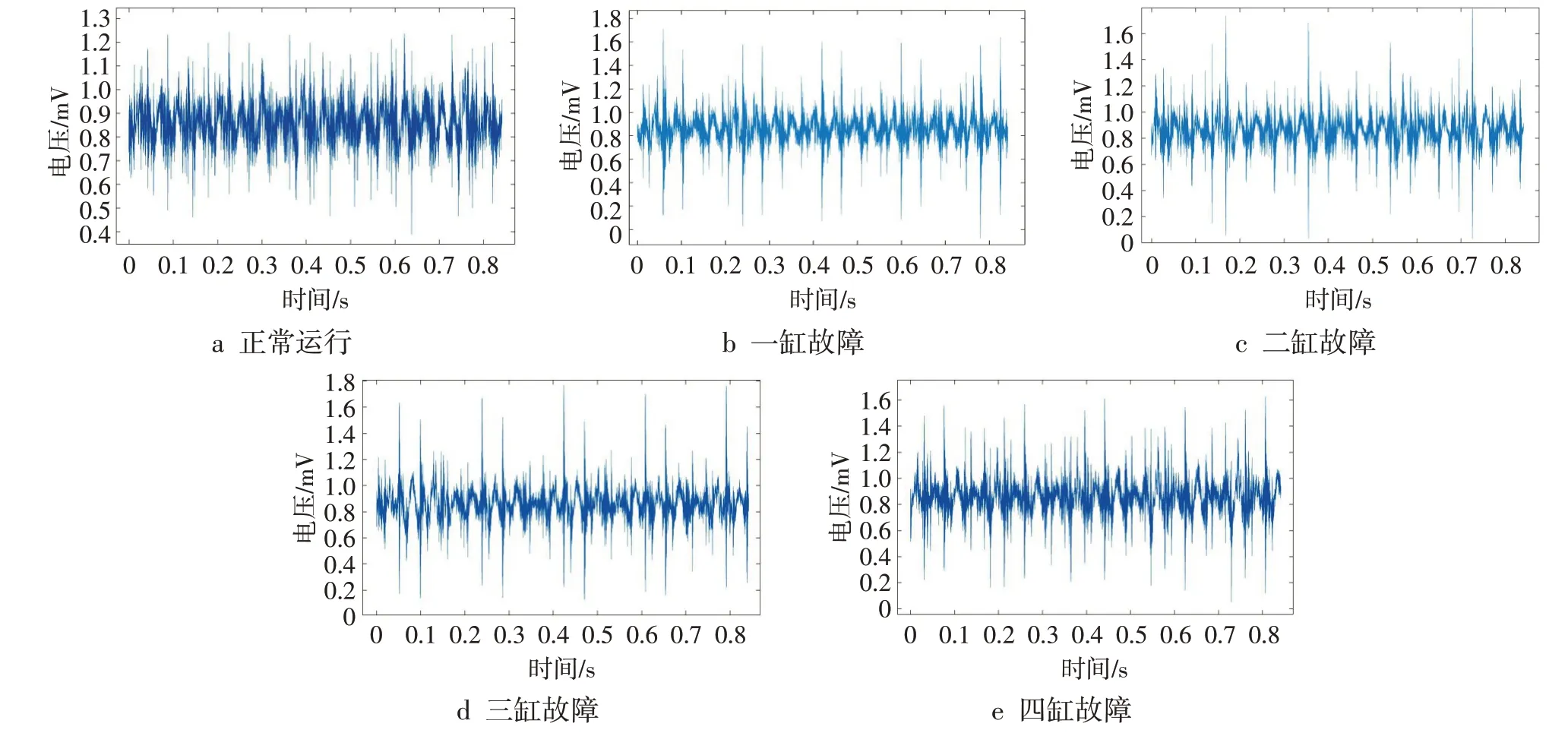
图3 各工况下振动信号时域图

2）小波包分解 文中采用的小波函数为db3，分解层数为3层。以正常工况下小波包分解为例，利用MATLAB 软件进行小波包的分解，如图4 所示。经过小波包分解后该信号第3 层每个节点的能量值可以算出，如图5所示。每个节点能量比例如表3所示。

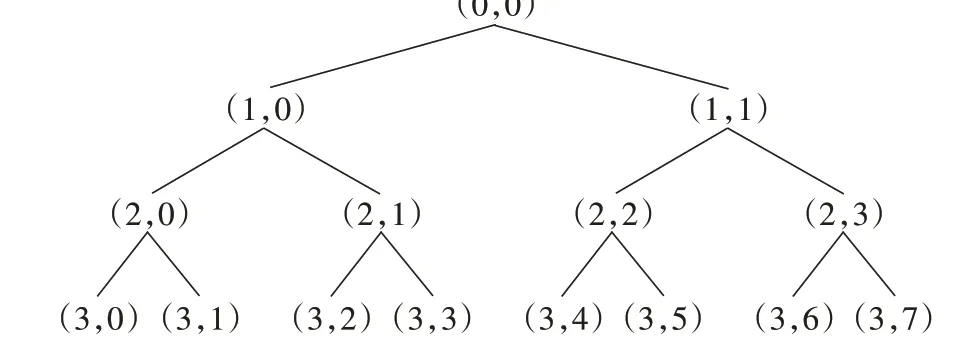
图4 正常工况下小波包分解结构图

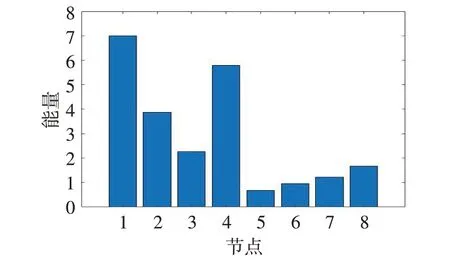
图5 节点能量值示意图

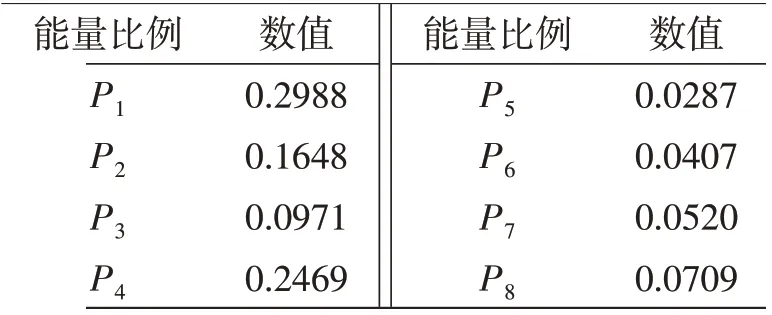
表3 节点能量比例

3）特征向量计算 从原始数据中每种工况选出1 组数据作为示例，根据式（4）计算出振动信号的WEE、S、PP，并建立不同运行状态下的三维特征向量，5组样本特征向量计算结果汇总如表4所示。

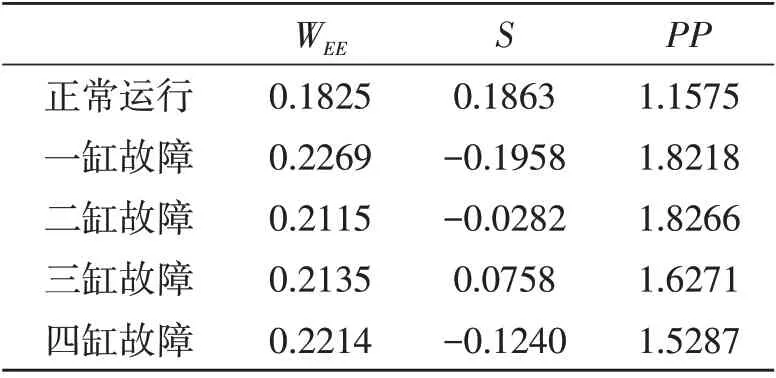
表4 特征向量结果

4 故障诊断模型研究

4.1 基于SVM的电控发动机故障诊断

经上述实验数据处理方法处理后，每种运行情况得到20组特征向量，共100组特征向量，随机选出80 组作为训练样本用于训练SVM 模型，其余的用于测试模型，结果如图6所示，纵轴数字0代表发动机正常运行，数字1表示一缸故障，数字2表示二缸故障，数字3 表示三缸故障，数字4 表示四缸故障。结果表明：20 组测试样本中只有2 组预测错误，样本8将二缸故障预测为四缸故障，样本14将一缸故障预测为四缸故障，其余18 组预测结果与实际结果一致，模型的预测准确率达到90%。

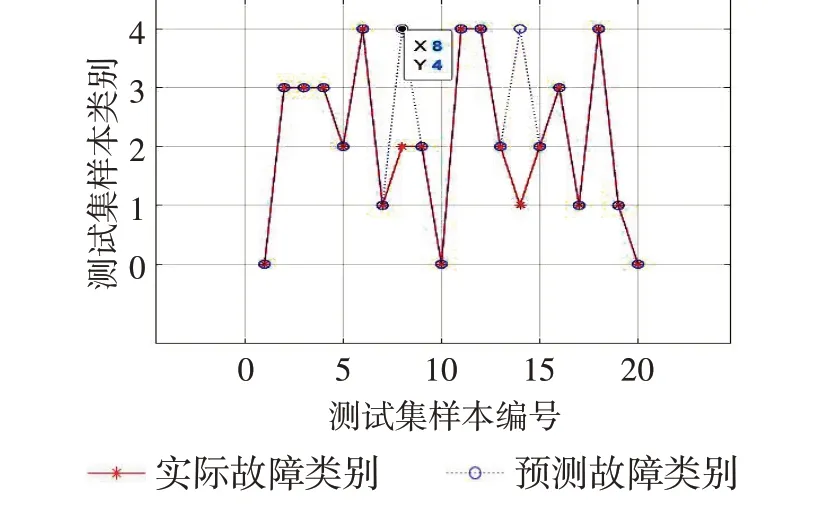
图6 SVM预测与测试结果对比图

4.2 基于BP神经网络的电控发动机故障诊断

BP 神经网络作为分类识别的常用方法，在发动机故障诊断中的应用效果较好，得到较广泛的应用。文中建立的故障诊断BP神经网络模型对电控发动机进行故障诊断，故障样本、故障特征提取方法以及提取的特征向量均与基于SVM的故障诊断方法相同。

每种工况选择的特征向量数目、训练样本与测试样本数目均与基于SVM 的故障诊断方法相同，训练过程如图7 所示，训练集最小均方误差在第5代达到目标要求，BP神经网络收敛，第5代之后呈下降趋势但不明显，且在第10 代候下降趋势稍有变陡。测试结果如图8所示，纵轴数字1代表发动机正常运行，数字2表示一缸故障，数字3表示二缸故障，数字4表示三缸故障，数字5表示四缸故障。分析结果表明：20 组测试样本中有4 组预测错误，样本9将二缸故障预测为正常工况，样本13将一缸故障预测为三缸故障，样本15 将正常工况预测为四缸故障，样本18将一缸故障诊断为二缸故障，在判断错误的样本中没有出现完全诊断错误，只有4个样本未能正确分类，其余16 组测试样本预测结果与实际结果一致，模型的预测准确率达到80%。

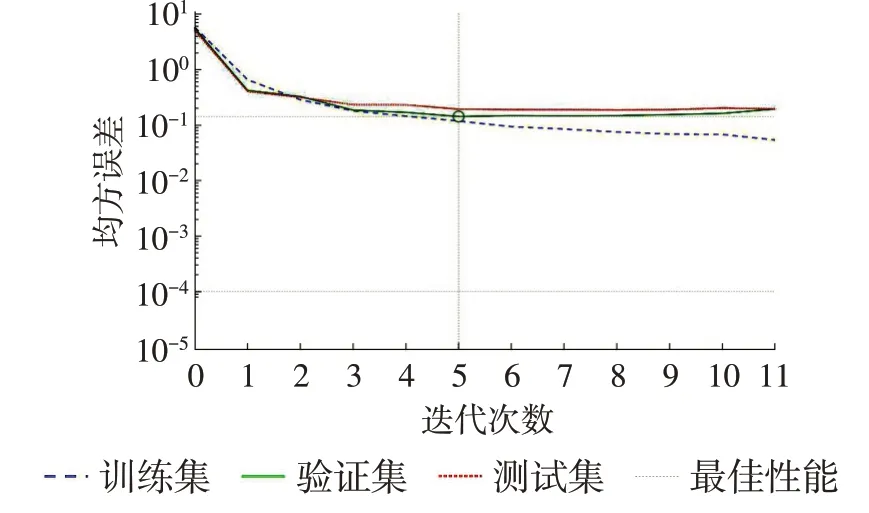
图7 BP神经网络训练过程

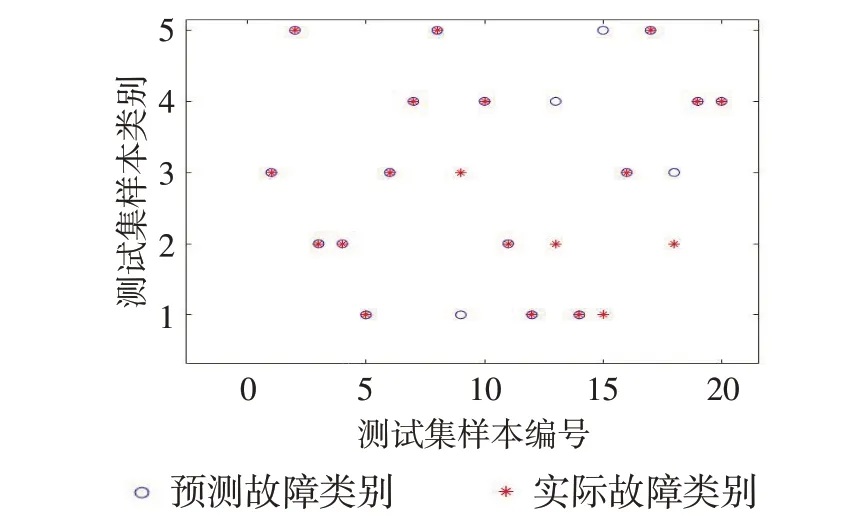
图8 BP神经网络测试结果

4.3 模型对比分析

SVM 与BP 神经网络都取得良好的效果，通过对2 种模型的结果对比，得出以下结论：1）SVM 预测准确率相比于BP 神经网络较高，且对样本特征向量的容错率更强；2）SVM的误差相对较小，模型较为稳定，且算法更简洁方便，实用性更强；3）SVM解决有限数量样本高维数模型问题上有较强的泛化能力，但数据为大样本数据时训练速度比较缓慢；当数据样本较大或者分类需求较多时BP 神经网络的优势更大。

5 结论

文中将采集到的振动信号进行小波包分解并计算得出小波能谱熵，将小波能谱熵与时域特征中的峰峰值和偏度组成三维特征向量，将特征向量输入SVM 模型进行学习与预测，预测结果正确率达到90%。利用BP 神经网络进行对比试验，正确率达到80%。结果表明：将小波能谱熵、峰峰值、偏度组成故障诊断特征向量，从诊断结果上来看，较好地反映了故障的特征；基于SVM 的故障诊断模型能有效对电控发动机进行故障诊断，提高了故障诊断精度，鲁棒性较强，实用性及工程应用价值较强。