混合式永磁调速器导体转子振动影响因素分析
宗昌盛,高庆忠,何雨桐,杨柏
(沈阳工程学院自动化学院,辽宁省 沈阳市 110136)
0 引言
永磁调速器作为一种新型的传动装置具有安全性高、故障效率低、维护少、安装简单、无谐波和环境污染等优点,可实现电机缓冲启动,在大型船舶动力系统、石油化工、电厂、污水处理等领域中有着广泛的应用。
由于永磁调速器的运用,负载与电机实现无直接机械连接,提高了系统的传动效率,降低了系统故障率。通过改变永磁调速器导体转子与永磁体转子之间的气隙长度实现调速,在改变气隙长度的过程中调速器会发生较大的振动,因此必须对永磁调速器的振动特性做研究分析。
近年来专家学者针对永磁调速器振动问题展开了一系列的研究,并且取得了一定的研究成果。王旭[1]提出了一种开槽式导体盘的永磁调速器,提高了调速器的传动效率;张宏刚[2]研究了在相同外形尺寸和磁路尺寸条件下,磁极数目对永磁调速器振动的影响,结果表明,随着磁极数目的不断增大,振动幅度逐渐减小。杨超君等[3-4]对双层实心与鼠笼转子异步磁力联轴器的涡流场进行了特性分析,研究了涡流场对传动效率的影响;李桃等[5]对盘式永磁调速器进行三维运动涡流场有限元仿真,并分析其机械特性。刘岩等[6]研究了混合式永磁调速器整体温度场,并且对比分析有无散热筋对混合式永磁调速器散热的影响。
目前对永磁调速器的研究多集中在基于盘式或筒式单一结构下的磁场和涡流场分析上。本文研究的是一种混合式永磁调速器结构,这种混合式结构既具有径向磁路,又具有轴向磁路,可增大永磁调速器的转矩和功率密度。但这种混合式结构是否对永磁调速器的振动效果具有影响还没有研究。大多数文献都是研究永磁体转子对永磁调速器振动的影响[7],很少有文献研究导体转子对永磁调速器振动影响。本文采用有限元仿真技术对永磁调速器导体转子的振动模态和固有频率进行研究,并建立三维运动振动的数学模型,利用有限元仿真软件探讨永磁耦合调速器导体转子(铜环与铜盘)厚度对振动特性的影响,最后通过仿真验证了所提方法的正确性。
1 混合式永磁调速器转子仿真模型
混合式永磁调速器是盘式永磁调速器与筒式永磁调速器的组合,混合式永磁调速器提高了调速器的传动效率。混合式永磁调速器的转子(导体转子与永磁体转子)由径向转子与轴向转子2部分构成。混合式永磁调速器转子参数如表1所示,仿真模型如图1所示。

表1 混合式永磁调速器转子参数Tab. 1 Rotor parameters of hybrid permanent magnet governor
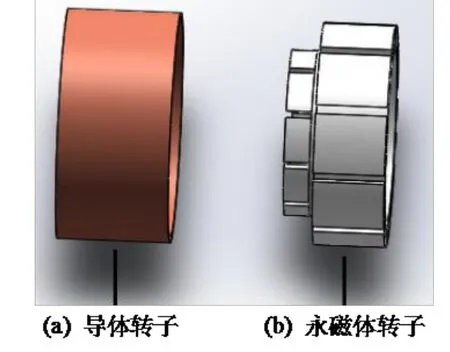
图1 混合式永磁调速器转子仿真模型Fig. 1 Simulation model of hybrid permanent magnet governor rotor
2 振动特性分析
2.1 振动原因分析
1)永磁调速器振动的主要原因是导体转子与永磁体转子在气隙磁场的径向分量作用下产生磁力波[8]。大量研究表明:虽然磁力是直接作用在导体上,但导体与外壳主要振动的根源是导体和永磁体。
2)永磁调速器的永磁体是由钢盘永磁体组成,永磁体是镶嵌在钢盘上,由于生产技术与制造工艺误差会造成永磁体出现轴不对称情况。同时,在生产与组装时也会产生误差与磨损等诸多不利因素。此外,永磁调速器在运行过程中会引起永磁体转子与导体转子局部过热,这些都会导致导体对于永磁体偏心,造成不平衡的磁拉力,使永磁调速器产生振动[9]。
3)由于永磁调速器永磁体的大小、形状、数目不同,所产生的磁力和磁场分布不均衡,从而导致导体产生振动。
4)固有频率是物体本身具有的一种属性,当永磁调速器内部机磁力的频率等于永磁调速器本身的固有频率时,就会发生共振现象,共振会导致调速器产生猛烈振动,对整个系统结构造成严重危害。
2.2 导体转子振动模态的数学模型
设轴向导体转子壳体长度为L,h为轴向导体转子壳体厚度,ρ为导体转子材料密度,E为杨氏模量,μ为泊松比。x、s、z分别为导体转子轴向、沿导体截面周向、截面径向坐标。设u、v、w为导体转子中面的轴向、周向、径向位移,R为截面的曲率半径。

根据Donnell壳体理论[10]可得:式中:(θ1,θ2,δ)与(k1,k2,φ)分别是在x、s、z方向的形变和曲率;xθ、sθ、xsφ分别为各个方向应变与位移的关系。
层合圆柱壳体的物理方程为


式中:Qij为材料刚度系数。
导体转子轴向运动平衡方程为


式中:Emn(t)为广位移;M、N分别为轴向与周向的Galerkin 截断阶数;φm(x),φn(s) 为径向转子影响轴向转子边界条件的试函数。

式中C*,K*的矩阵中含有轴向速度项,可由式(11)分析导体转子振动特性。
3 有限元仿真分析
本文分别对不同厚度导体转子(铜环与铜盘)进行振动仿真分析。利用有限元仿真软件SolidWorks建立仿真模型,分析仿真结果,得出影响永磁调速器振动因素[11-13]。
3.1 不同厚度导体转子有限元仿真分析
通过对不同厚度导体转子进行有限元仿真,分别得到频率为2 500 Hz,4阶模态下不同厚度导体转子的振动仿真结果(见图2)和不同厚度导体转子在相同转速下的振动质量参与系数(见表2)。
由图2和表2可知,铜环与铜盘的厚度相同时,随着导体转子厚度的增加,其振动程度也逐渐增加;其中s方向与z方向振动增加幅度比x方向迅速。铜盘厚度相同时,随着铜环厚度的增加,导体转子的振动程度也逐渐增加,铜环厚度大于铜盘时,s方向与z方向振动增加幅度大于x方向。导体转子的厚度对其在x方向的振动影响甚微;铜环厚度是影响s方向与z方向振动幅度的主要因素。铜盘与铜环厚度的差值越大,振动增加幅度越大,当导体转子厚度≥11 mm时,导体转子s方向与z方向的振动急剧增大。

图2 不同厚度导体转子振动仿真结果Fig. 2 Vibration simulation results of different thickness conductor rotor
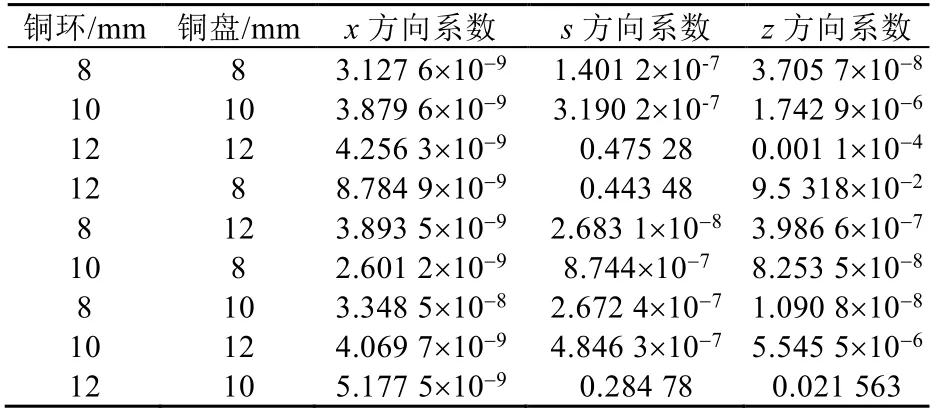
表2 不同厚度导体转子在相同转速下的振动质量参与系数Tab. 2 Vibration mass participation coefficient of a conductor rotor with different thickness at the same speed
3.2 不同厚径比与长径比导体转子有限元仿真
通过对不同厚径比与长径比导体转子进行有限元仿真,得到转速为1 000、2 000 r/min时不同厚径比与长径比导体转子的振动质量参与系数变化曲线,分别如图3、4所示。

图3 不同厚径比导体转子的振动质量参与系数变化曲线Fig. 3 Curves of vibration mass participation coefficient of conductor rotor with different thickness to diameter ratio
由图3可知,不同厚径比导体转子在1 000、2 000 r/min下的振动质量参与系数变化相差不大。随着导体转子厚径比增大,振动质量参与系数逐渐增大,s方向与z方向的质量参与系数高于x方向,s方向与z方向的质量参与系数的变化率大于x方向。
由图4可知,不同厚径比导体转子在1 000、2 000 r/min下的振动质量参与系数变化趋势相同,2 000 r/min下的振动质量参与系数整体高于1 000 r/min,因为转速加大,轴向导体转子对径向导体转子的约束力减小。随着导体转子长径比增大,振动质量参与逐渐系数减小。s方向与z方向的质量参与系数及其变化率高于x方向。
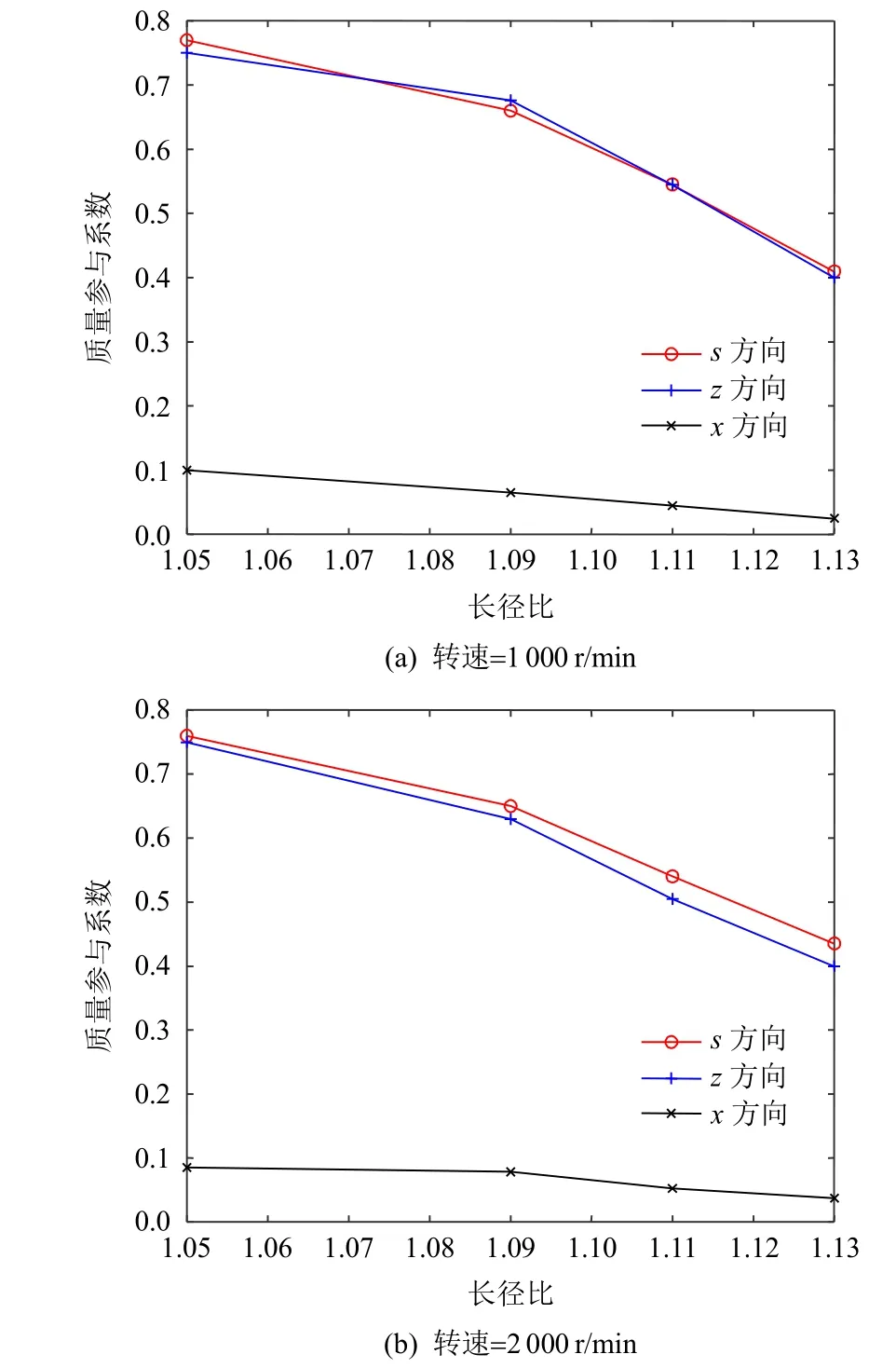
图4 不同长径比导体转子的振动质量参与系数变化曲线Fig. 4 Curves of vibration mass participation coefficient of conductor rotor with different aspect ratio
4 结论
研究了混合式永磁耦合调速器的振动问题,分析了引起混合式永磁耦合调速器振动的原因,利用有限元软件仿真得到混合式永磁耦合调速器导体转子振动结果,得出以下结论:
1)导体转子整体振幅比铜环与铜盘单独振幅要小,表明铜盘对铜环起到相互抑制振动的效果,铜盘相对于铜环具有外界条件约束作用。
2)在相同条件下,径向导体转子与轴向导体转子的厚度差值越大,导体转子整体的振动效果越差,轴向导体转子是影响导体转子整体振动的主要因素。
3)导体转子振动效果随厚径比增大而增大,随长径比增大而减小。

