基于Kolmogorov熵的气固鼓泡流化床中空隙率波动信号分析

韩峰，丛堃林，向杰，李清海，张衍国*，马静,

（1.北京热华能源科技有限公司，北京市 海淀区 100085；2.清华大学能源与动力工程系，北京市 海淀区 100084；3.润电能源科学技术有限公司，河南省 郑州市 450000）

0 引言

能源的清洁高效利用关系到国家的能源安全和生态环境保护，工业锅炉作为传统工业中一种重要的热能动力设备，效率低、污染物排放浓度高造成的能源浪费和环境污染问题亟待解决。 为了满足工业锅炉容量小、布点散的使用需求，同时保持传统循环流化床高效清洁燃烧的技术优势，国内学者开发了多流程循环流化床燃烧技术及系列化锅炉[1]，并对其进行了一系列研究和应用[2-7]。流化床内的气固流动状态决定了流化床中气固两相的混合、传热和传质特性[8-9]，因此，研究气固流动状态对流化床锅炉的优化设计、稳定运行和状态监测起着十分重要的作用。

气固流动状态的研究方法有很多种，包括理论计算、数值模拟和实验分析等。通过仪器测量流化床内的物理波动信号并进行数值分析，是研究流化床内气固流动的动力学特性的一种重要方法。常用的表征流化床气固流动状态的物理信号有压力、空隙率、气相和颗粒相的速度、声音和振动等[10-14]。其中，空隙率信号与流化床内气泡的行为密切相关，能够反映流化床内局部区域气相和颗粒相结构的变化[15]，因此，空隙率信号与流化床内的物理过程的联系更为清晰。

信号分析的方法主要有时域分析[16]、频域分析[17]和混沌分析等。基于以往学者对于气固流化床中空隙率波动信号的研究，认为空隙率波动信号表现出明显的混沌特性。常用的混沌特征量有关联维和Kolmogorov熵。关联维表示了混沌系统的自由度的大小，但其变化不敏感[18]。与之相比，Kolmogorov熵对操作条件的变化更敏感，因此常被用于定量表征流化床的混沌特性，Kolmogorov熵越大，系统的混沌程度越大，系统越复杂。

本文以气固鼓泡流化床为研究对象，以空隙率波动信号作为分析对象，在实验室内搭建了冷态实验装置，采用颗粒浓度测量仪测量了不同工况条件下流化床床中心的空隙率波动信号，从测量得到的空隙率波动信号中提取表征气固流动状态的Kolmogorov熵，研究表观气速、静床高度和床体尺寸对Kolmogorov熵的影响规律，进而更好地理解气固鼓泡流化床的流动机理。

1 Kolmogorov熵

Kolmogorov熵K是用于表征混沌系统不可预测性程度的特征量，描述了混沌轨道随时间演化信息的产生率，单位为bits/s或nats/s。对于完全可预测的系统，K=0；对于随机系统，K=∞，为完全不可预测的系统；对于混沌系统，K为一个有限正数。

文献[18]提出了通过计算2阶Renyi熵K2来逼近Kolmogorov熵的思想，假定吸引子上不同轨道相邻点的演化按指数分离，2个初始邻近点的距离超过l0所需的时间为t0，满足指数分布

式中b为采样时间间隔的数量。

t0可以用b个采样时间间隔表示：

式中τs为采样时间间隔。

找到刚好经过b个采样时间间隔后大于l0的初始点间距的概率为

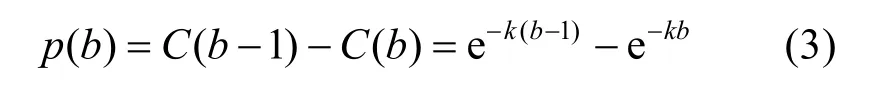
式中k=Kτs。

基于以上研究，文献[19]提出了一种用于估算Kolmogorov熵及其标准误差的最大似然法。

式中M为b的样本量。

2 实验及测量系统

2.1 实验装置

实验装置由3部分组成，分别为流化床床体(流化床+布风板+风室)、测量系统(颗粒浓度测量仪+控制软件+计算机)和供风系统(阀门+流量计+离心风机)，如图1所示。为了便于观察气固鼓泡流化床内的气固流动状态，流化床床体采用有机玻璃制作而成。布风板同样由厚度8 mm的有机玻璃制作而成，风孔的孔径为1 mm、孔间距为10 mm，均匀布置在布风板上。

在流化床床体尺寸选择上，为了研究床体尺寸的影响，选用了4种不同尺寸的床体横截面，分别为3种正方形截面(边长为5、10和15 cm)和1种矩形截面(边长为2 cm×10 cm)，其水力直径Dt依次为5、10、15和3.3 cm。当床体尺寸发生变化时，布风板的尺寸做相应变化，但孔板的厚度、风孔的孔径和孔间距不变。

空隙率波动信号通过流化床壁面上的测孔(垂直于壁面的长30 mm、内径6 mm的有机玻璃管段)进行测量。测孔布置在流化床的一个侧面的中心线上，如图1中的P1—P4所示，P1测孔距离布风板2 cm，P2测孔与P1测孔相距4 cm，P2测孔到P4测孔以5 cm为间距均匀布置。

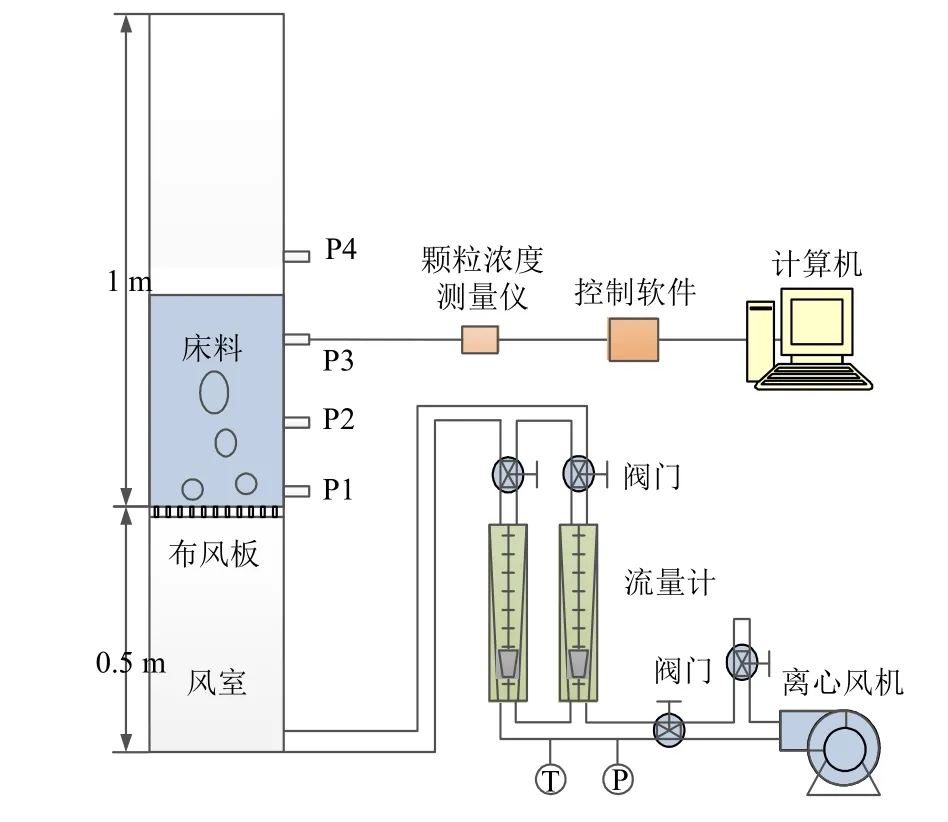
图1 实验系统Fig. 1 Schematic diagram of experiment system

2.2 测量系统

局部空隙率波动信号采用PC6M型4通道颗粒浓度测量仪测量，该颗粒浓度测量仪应用光导纤维阵列探头检测与运动颗粒浓度相关的反射光信号，实物照片和光纤探头端部示意如图2所示。

图2 颗粒浓度测量仪及其探头端部示意Fig. 2 Schematic diagram of particle concentration meter and its probe end

测量空隙率时，从流化床壁面测孔将光纤探头插入床内，采用4根探头同时测量，通过控制软件设置采样频率为1 000 Hz，采样时长为65 s或131 s，将采集的数据记录到计算机上。

实验测量的空隙率信号为最大值为5 V的电压信号，使用前需要标定空床、满床，拟合空隙率信号与电信号的曲线，可以得到简单的换算公式。实验中测得满床的空隙率为0.42，空床的空隙率为1。

2.3 颗粒特性

实验中流化床选用的床料为玻璃珠，其粒度分布如图3所示。玻璃珠平均粒径为246 μm，密度为2 500 kg/m3。经测量，玻璃珠的松散堆积空隙率为0.42，最小流化风速为0.064 m/s，属于Geldart B类颗粒。

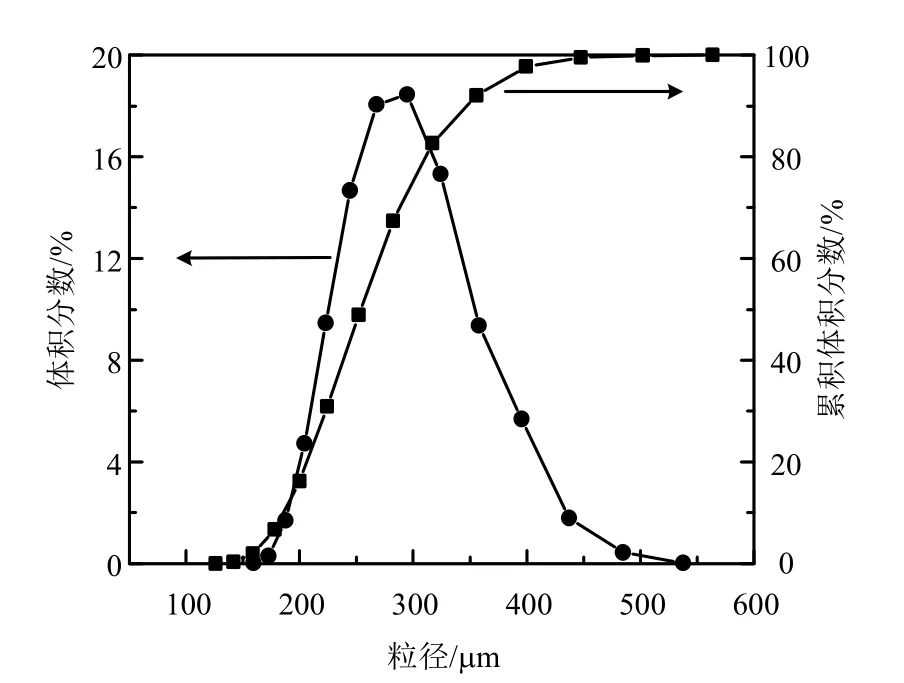
图3 玻璃珠的粒度分布Fig. 3 Particle size distribution of glass beads

3 结果与讨论

采用颗粒浓度测量仪对流化床不同轴向高度床截面中心的空隙率波动信号进行测量，获得空隙率的时间序列，进而利用混沌分析的方法计算其Kml熵，研究表观气速、静床高度和床体尺寸对Kml熵的影响规律。

3.1 表观气速的影响

4种不同床体尺寸的床中，不同轴向高度床中心空隙率波动信号的Kml熵随表观气速的变化如图4所示。

图4 不同高度的床中心空隙率波动信号的Kml熵随表观气速的变化情况Fig. 4 The change of Kml entropy with gas velocity at different heights

从图4可以看出，在表观气速较高时，Kml熵随着表观气速的增加总体上呈逐渐增大的趋势。如图4(b)所示，5 cm床的测孔P3和P4的Kml熵先略有减小再逐渐增大；如图4(c)所示，10 cm床的测孔P4的Kml熵在表观气速较高时几乎保持不变。

此外，对于3.3 cm和5 cm 2个小尺寸床，如图4(a)和(b)所示，Kml熵随轴向高度的增加而减小，不过测孔P3和P4的Kml熵很接近。主要是因为当气体经过布风板进入床层时，部分气体汇合形成气泡，气泡间的相互作用使布风板附近的两相运动更复杂；随着轴向高度的增加，气泡汇合和破裂的趋势下降，两相运动变得更加稳定，所以使P1、P2的Kml熵明显大于P3和P4的Kml熵。相比之下，如图4(c)和(d)所示，10 cm和15 cm 2个大尺寸床的这种变化趋势并不明显，说明床体尺寸对Kml熵随轴向高度的变化趋势影响较大。

但是在表观气速较低时，Kml熵随表观气速总体上呈现先增大后减小的趋势，这是床内颗粒相运动和气泡相运动共同作用的结果。如图4(c)和(d)所示，对于10 cm和15 cm 2个大尺寸床，Kml熵在表观气速较低时随表观气速的变化较为复杂，特别是15 cm床。对于10 cm床的测孔P1及15 cm床的测孔P2和P3，Kml熵随表观气速的增加先快速增大到极大值，再快速减小，然后再缓慢增大。对于15 cm床的测孔P1，Kml熵有剧烈的波动。说明在表观气速较低时，床体尺寸的影响更为显著。

3.2 静床高度的影响

静床高度对床中心空隙率波动信号的Kml熵的影响如图5所示。从图5可以看出，在表观气速较高时，气泡相产生的空隙率波动占主导作用，Kml熵随静床高度的增加总体上呈减小的趋势。测孔P4的位置距离布风板表面为16 cm，位于静床高度(13 cm)之上，气泡相产生的空隙率波动影响较大，因此，对应的Kml熵远大于18 和23 cm 2个静床高度下的值，如图5 (d)所示。

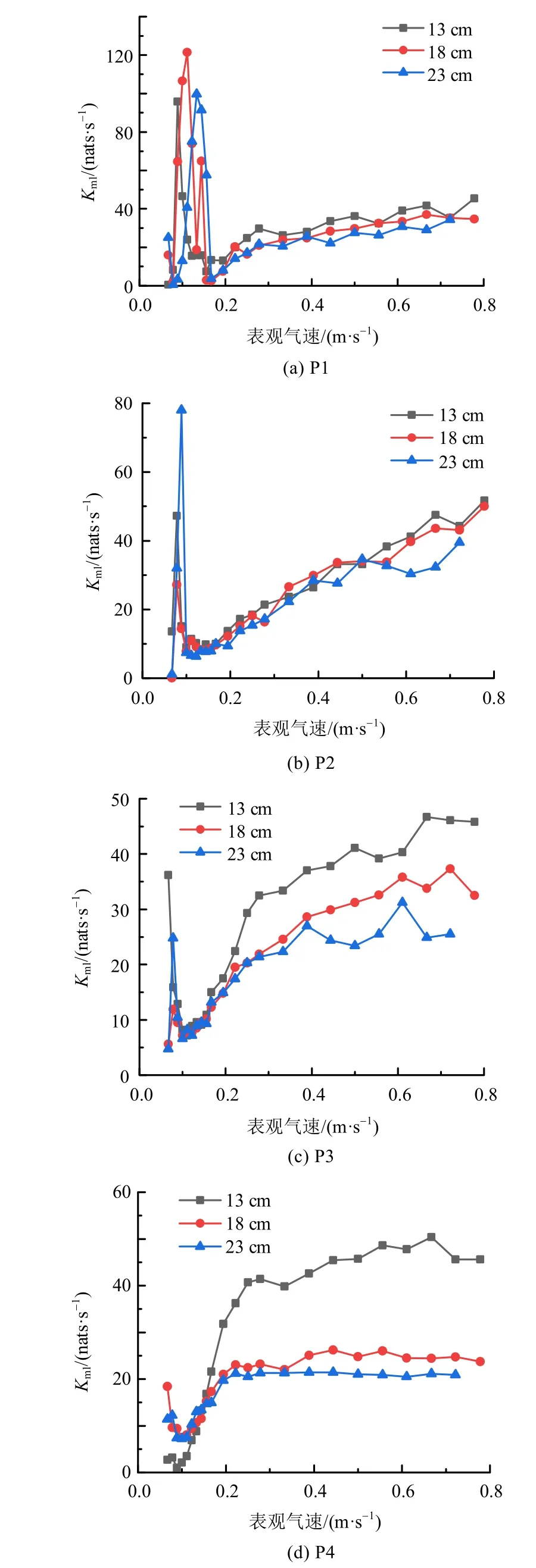
图5 静床高度对床中心空隙率波动信号的Kml熵的影响Fig. 5 The effect of static bed height on Kml entropy

在表观气速较低时，Kml熵出现一个极大值，在这个过程中空隙率波动信号由颗粒相空隙率波动占主导作用向气泡相产生的空隙率波动占主导作用转变。测孔P1的Kml熵出现极大值时对应的表观气速随静床高度的增加而增加；此外，不同静床高度的Kml熵在表观气速较低时差别较小。

3.3 床体尺寸的影响

床体尺寸对床中心空隙率波动信号的Kml熵的影响如图6所示。

图6 床体尺寸对床中心空隙率波动信号的Kml熵的影响Fig. 6 The effect of bed size on Kml entropy

从图6可以看出，对于测孔P1和P2，在表观气速较高时，除了3.3 cm床，Kml熵随床体尺寸的增加而减小。对于测孔P3和P4，床体尺寸对Kml熵的影响没有明显规律，5 cm床的Kml熵随表观气速的增加先增大后减小再增大，不同于其他尺寸的床随表观气速逐渐递增的趋势。由于测孔P1和P2靠近布风板，受床体尺寸的影响要远大于测孔P3和P4。

在3.3 cm床中，测孔P1的Kml熵处于5 cm和10 cm床之间；测孔P2的Kml熵在表观气速较低时与10 cm床的值几乎重合，而在表观气速较高时略高于5 cm床的值，这说明矩形截面布风板的影响较大。在10 cm床中，测孔P4的Kml熵在表观气速较高时变化很小。

4 结论

气固鼓泡流化床系统具有正Kml熵，说明其为一个具有混沌行为的动力学系统。总体而言，表观气速、静床高度和床体尺寸都会对Kml熵产生影响，其中，表观气速对Kml熵的影响最大，静床高度次之，床体尺寸最小，具体结论如下。

1）表观气速大于0.2 m/s时，随表观气速的增加，Kml熵总体上呈逐渐增加的趋势，对于3.3 cm和5cm 2个小尺寸床，Kml熵随轴向高度增加而减小，主要是因为床体尺寸小导致布风板附近两相运动比较复杂；表观气速小于0.2 m/s时，Kml熵随表观气速总体上呈先增大后减小的趋势。

2）在表观气速较高时，Kml熵总体上随静床高度增加而呈减小的趋势；在表观气速较低时，Kml熵在空隙率信号由颗粒相空隙率波动占主导作用向气泡相产生的空隙率波动占主导作用转变过程中出现极大值。

3）对于测孔P1和P2，表观气速较高时，除了3.3 cm床，Kml熵随床体尺寸的增加而减小；对于测孔P3和P4，床体尺寸对Kml熵的影响没有明显规律。由于测孔P1和P2靠近布风板，受床体尺寸的影响要远大于测孔P3和P4。

4）在实际气固流化床的设计、控制和放大中，应对布风板附近的两相运动状态进行着重考虑。