基于深度小世界神经网络的风电机组异常检测

李亚光，李蒙

（1.华电煤业集团有限公司，北京市 西城区 100035；2.北京交通大学机械与电子控制工程学院，北京市 海淀区 100044）

0 引言

恶劣多变的环境是风力发电机故障频发的主要原因[1-6]。一般情况下，风机的各个系统中都安装有各类状态监测传感器，并由数据采集与监视控制(supervisory control and data acquisition，SCADA)系统对监测参数进行记录和保存[7]。一旦有异常发生，设备的故障信息将反馈到多维传感器参数中[8]。因此，利用SCADA数据进行早期异常检测，将有利于实现风电机组的状态评估和故障预警。

通常情况下，故障检测与隔离(fault detection and isolation，FDI)的方法有2个关键过程：1）从复杂数据中提取有效特征；2）利用先验知识或机器学习技术实现故障分类。值得注意的是，这2个步骤都需要明显的标签信息(正常或异常标签)作为训练智能分类算法的基本要素[9-10]。但在实际的风机SCADA系统中，几乎不可能获得足够的标签数据。这是因为正常运行时间比故障发生时间长很多，导致数据稀疏是不可避免的。另外，SCADA的监控数据和故障信息大多是分开记录的，它们之间的相关性只能在故障发生后由人工来完成。这种非智能化的记录和分类工作是巨大的，也是不现实的。因此，利用不完善的无标签数据来完成风电机组的FDI任务充满了挑战。

深度学习方法[11]以其良好的非线性逼近性能已经在数据挖掘和智能故障诊断中得到了广泛应用[12]。与浅层神经网络相比，一些深度学习算法[13]，如多层感知器、深度神经网络(deep neural network，DNN)、长短期记忆网络(long-short-term memory，LSTM)和卷积神经网络(convolutional neural network，CNN)等，均可以模拟人类真实的学习过程，并从数据中挖掘有价值的信息。Jiang等人[14]提出了一种多尺度卷积神经网络，用以有效地学习高层故障特征。Yang等人[15]利用LSTM递归神经网络挖掘SCADA信号中隐藏的时空关系，实现了风机齿轮故障的分类。面对SCADA系统采集的大量文本数据，近年来的研究工作创新性地将其转化为图像或地图形式，然后利用图像识别算法进行异常检测和识别。例如，文献[16-17]将振动信号转换成时域谱，应用CNN提取故障特征。然而，上述网络的实现需要基于有监督的和足够标签的学习环境下进行，这在实际应用中却很难实现。

使用无监督学习构造的深度神经网络也相对成熟[18]，相应的算法主要包括受限玻尔兹曼机(restricted Boltzmann machine，RBM)或自动编码器(auto-encoder，AE)。深度置信网络(deep belief network，DBN)[19]、去噪自编码器(denoise auto-encoder，DAE)[20]和堆叠自编码器(stacked auto-encoder，SAE)[21]是最具代表性的无监督深度神经网络。Qin等[22]用DBN诊断风力发电机行星齿轮箱故障，提出了改进的Logistic-sigmoid单元和脉冲特征法，解决了DBN在反向传播中容易出现梯度消失的问题。Qin等[23]在多层BP神经网络的基础上建立了一个深度SAE网络，利用来自SCADA系统的方位数据，通过无监督贪婪学习对SAE网络神经元进行逐层训练，再将训练后的权值作为深度BP神经网络的初始权值。此外，Zhao等[24]还提出了一种基于多层Boltzmann机的深度自编码网络，以实现风力发电机组部件的早期异常检测和故障检测。

目前，随着应用领域的不断变化，对神经网络的结构进行改进主要有加深网络层次、丢包与丢包连接、批量规范化等方法。其中，增加非相邻隐含层之间的连接边(添加边)方法是目前神经网络缓解梯度消失的研究热点。从网络结构上看，通过加边改进使得传统的神经网络成为一个小世界神经网络，已可应用于风力发电的功率预测[25]和风机变桨系统的故障诊断[26]。因此，本文结合风电机组的SCADA数据特点，基于深度自动编码网络的原型结构，提出一种深度小世界神经网络(deep small-world neural network，DSWNN)，以期进一步解决风电机组的早期故障检测与预警问题。未标记的风电机组SCADA数据被用于预先训练DSWNN原型以提取隐含特征。通过随机加边法将规则神经网络转化为一个小世界网络，并在有监督的情况下利用标记数据训练重构的DSWNN模型，对网络的全局参数进行微调。

由于实际运行中风速的随机变化和干扰，固定的故障判断阈值往往不合理，容易造成误报警。本文提出一种基于极值理论的自适应阈值作为异常检测判断的准则。通过上述方法构造的DSWNN模型具有良好的深度挖掘数据特性。最后，以风力机变桨系统为例，验证了该方法的有效性和准确性。

1 深度小世界神经网络模型构建

1.1 深度小世界神经网络结构

深度自编码网络是一种在输入层和输出层之间具有多个隐含层的深度神经网络。该网络的参数通过对输入数据逐层进行无监督学习来初始化，然后利用有监督学习进行微调，在较高的输出层产生更复杂的特征，并且学习到的复杂特征将随着输入数据的变化而保持不变。基于深度自编码网络结构，本文在非相邻隐含层之间增加了额外的神经元连接，进而构建了由多个RBM堆栈组成的具有4个隐含层的深度小世界神经网络，如图1所示。它的训练过程包括预训练、小世界转换和微调3个阶段，用于获取DSWNN模型的参数。

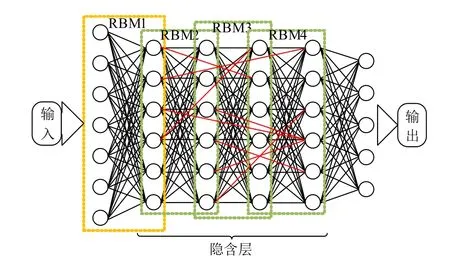
图1 深度小世界神经网络结构Fig. 1 Structure of DSWNN model

1.2 DSWNN原型的预训练

DSWNN模型的原型是一个具有多个基于特定能量的随机RBM的深度自动编码网络。图2所示RBM结构具有一个可见层和一个隐含层，其中可见神经元与隐含神经元完全相连。

图2 RBM结构Fig. 2 Structure of RBM

多层RBM的训练是在无监督环境下逐层实现的，可作为DSWNN原型的预训练过程。经过逐层预训练后得到整个网络的权值，将被记录并用作后续监督训练(微调)的优先值。

1.3 DSWNN网络的小世界转换

小世界网络是介于完全随机和完全规则之间的中间网络[27]。应用小世界网络的特性对人工神经网络结构进行改进[28]，主要有2种方式：重连变换和加边变换，如图3所示。

图3 小世界网络转换的方式Fig. 3 Transformation way of small-world network

以每层4个神经元的4层BP神经网络为例，重连变换首先随机断开相邻层神经元之间的连接，然后与非相邻层神经元之间随机地建立新的连接。而加边变换没有断开过程，它只在不改变任何原始边的情况下在非相邻层神经元之间添加新的连接。新增连接的位置都是随机分布在所有网络神经元之间的，网络的随机程度用概率p来描述。

式中nad和nor分别为新添加的连接数和原始连接数。

图4给出了从常规网络到随机网络的随机加边变换过程。当p=0或p=1时，网络是完全规则或完全随机的。当p介于0和1之间时，网络具有小世界属性。因此，利用特征路径长度L(p)和聚类系数C(p)对小世界结构性质进行量化，并探讨中间区域(0＜p＜1)的特性。

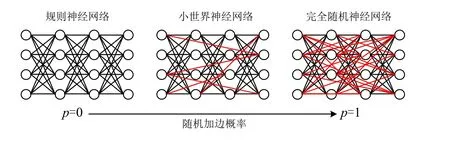
图4 从规则BP神经网络到随机网络的随机加边过程Fig. 4 Random add-edge procedure from a regular BP neural network to a random one

特征路径长度L(p)是衡量网络中所有连接边平均长度的全局性质，聚类系数C(p)是描述网络中连接边密度的局部性质。图5显示了图1中描述的4个隐含层DSWNN的L(p)和C(p)随p变化的规范化值。可以观察到，随着p的增加，L(p)急剧下降，而C(p)下降相对缓慢。当p接近0.1时，得到了一个大C(p)和一个小L(p)，这表明DSWNN的拓扑结构具有最好的小世界性质。因此，新添加的边连接数是原始连接数的10%。

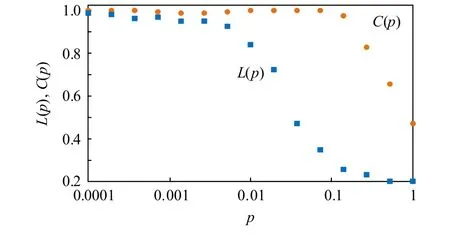
图5 图1中描述的4个隐含层DSWNN的L(p)和C(p)Fig. 5 L(p) and C(p) for the four-hidden-layer DSWNN described in figure 1

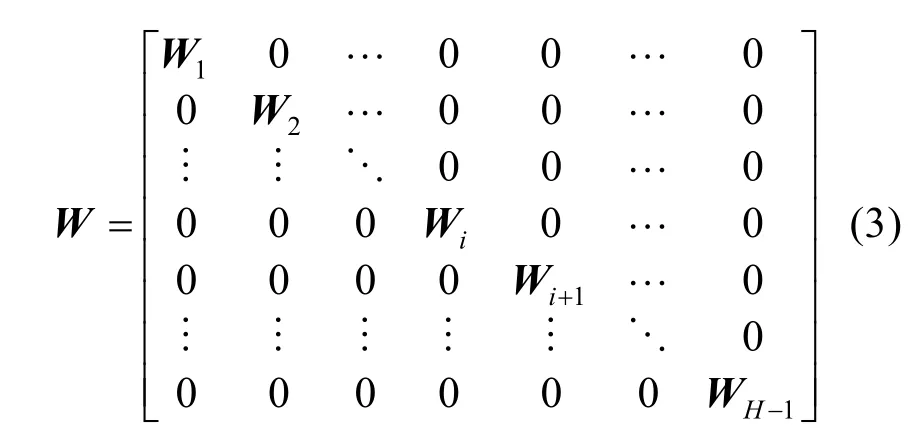
本文选择了加边变换方法来重建DSWNN模型。假设DSWNN模型有H(H=1,2,3,…,i,…)个隐含层，第i个隐含层有N个神经元，第i+1个隐含层有M个神经元。当p=0时，DSWNN模型是一个规则网络，第i层和i+1层之间的权重矩阵Wi被描述为

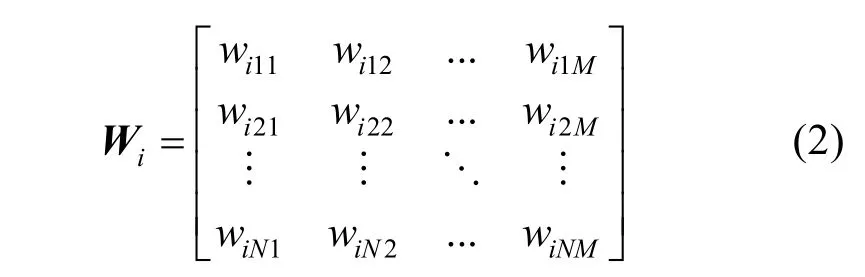
因此，整个隐含层的连接矩阵W可以表示为

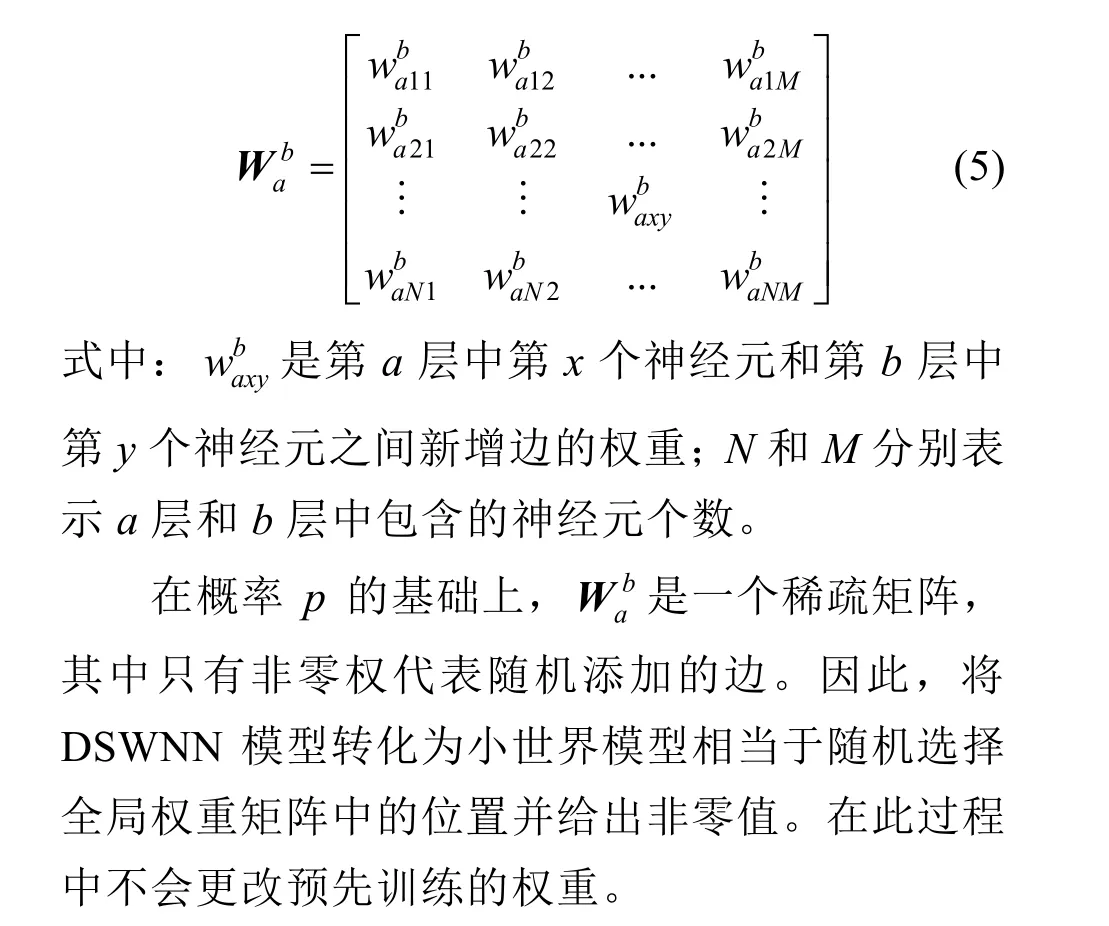
当p=0.1时，DSWNN不断开原始网络中的连接，只在非相邻隐含层中的神经元之间生成连接。矩阵W中的对角线权重不会改变，因为连接不会断开。整个隐含层的全局Wa可以表示为

1.4 DSWNN网络的参数微调

经过逐层预训练和小世界转换后，利用反向传播有监督学习BP算法对DSWNN进行微调，并在微调过程中优化隐含层的参数，最终得到了DSWNN模型的全局优化参数。在此过程中，DSWNN模型的初始参数由训练前参数(权值和偏差)和小世界转换得到的连接权值组成。由于微调只完成基于这些初始参数的局部搜索，因此在优化过程中大大缩短了收敛时间。

本文将tanh函数作为隐含层的激活函数，将Softmax函数作为顶层分类器的激活函数。选择公式(6)中所示的交叉熵[29]作为测量误差的代价函数C。

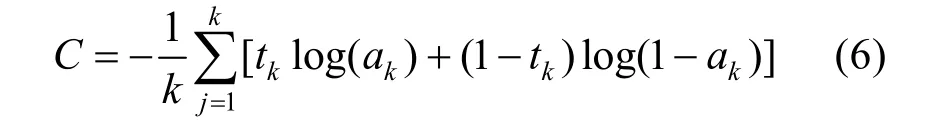
式中：k为输出层中的神经元数量；tk为输出层期望的输出标签值；ak为输出层实际预测值。

RBM训练过程可以看作DSWNN模型权值参数的初始化，克服了权值参数随机初始化容易陷入局部最优和训练时间长的缺点。对于故障的检测，可以使用大量未标记的SCADA数据进行预训练，使用少量标记的数据进行微调。这样，训练后的DSWNN比深度自编码网络或BP网络更为优化。

2 基于自适应阈值估计方法的异常检测

在异常检测中，利用训练好的DSWNN模型预测SCADA信号的未来值，并利用预测值与实际值之间的预测误差EP来判断异常。定义为

式中：X为SCADA数据的当前值；X^为DSWNN模型的预测输出。

一般来说，设定阈值并将其与EP进行比较是评估风电机组是否发生故障的最常用和最有效的方法。风机正常运行时，SCADA信号均在阈值范围内。一旦出现异常，这些监测信号之间的隐式关系将被打破，一个或多个信号值将突然超过阈值发出报警。确定异常情况的规则定义为

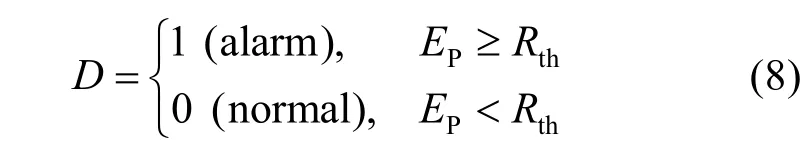
式中Rth是阈值。

然而，阈值的设置范围往往很广，且经常在初次设置后保持不变。一方面，阈值内的故障将无法诊断；另一方面，随机风速引起的一些偶然波动将被误诊为故障。因此，本文提出了一种基于极值理论的自适应阈值估计方法，用于监测EP的变化趋势，检测EP的异常变化。

假设X1，X2,…,Xn是分布函数为F(x)的独立随机变量的n个样本向量。每个样本向量Xi在一段时间内包含一定数量的值。Mn=max(X1，X2,…,Xn)表示n个样本向量的最大值。对于一组Mn，概率分布函数可以描述为

式中：an和bn分别是比例参数和位置参数；β是形状参数。

大量正常的SCADA数据被用来训练DSWNN模型，也被用来计算EP值。由于数据大多为正态分布，EP的均值是稳定的，但其方差数据应该是非平稳的。因此，比例参数an和位置参数bn分别表示为：

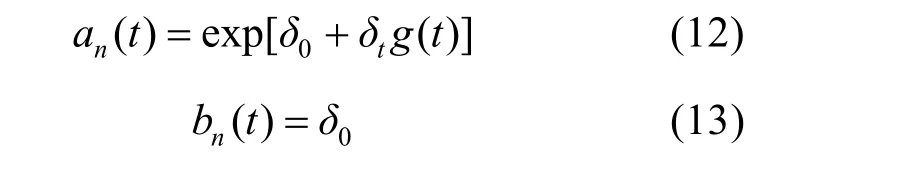
式中：δ0和δt均为常值系数；g(t)是描述受不断变化的SCADA数据影响的可变运行条件的函数。然后，用于确定警告的最终自适应阈值可以通过以下方法计算：

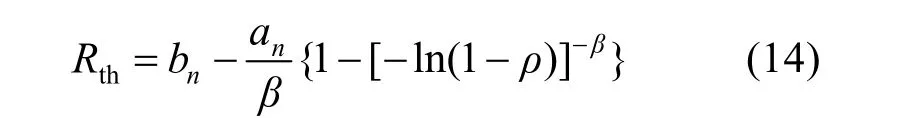
式中：ρ为置信度，由累积分布函数法计算而得；参数an、bn和β可通过最大似然估计方法来获得。

3 实例验证

3.1 风机变桨系统监测参数

为了测试所提出DSWNN模型的性能，在故障识别、预测和分类方面做实例分析。实验数据来源于某风电场30台2 MW风电机组一年的SCADA系统数据。另外，为了增加对比度，采用了经典DBN和DNN模型作为对比测试方法。俯仰故障主要分为俯仰传感器故障和执行器故障。变桨传感器故障是由编码器盘上的灰尘、叶片变桨轴承调整不正确、温度和湿度超出可接受范围或校准不当引起的。叶片变桨距传感器和执行器的这些故障经常出现，导致转子不平衡引起汽轮机结构负荷，影响浮动平台的稳定性。这些故障主要与俯仰角、俯仰力矩、俯仰电机等信号有关。用于训练DSWNN、DBN和DNN模型的特定监控SCADA参数如表1所示。

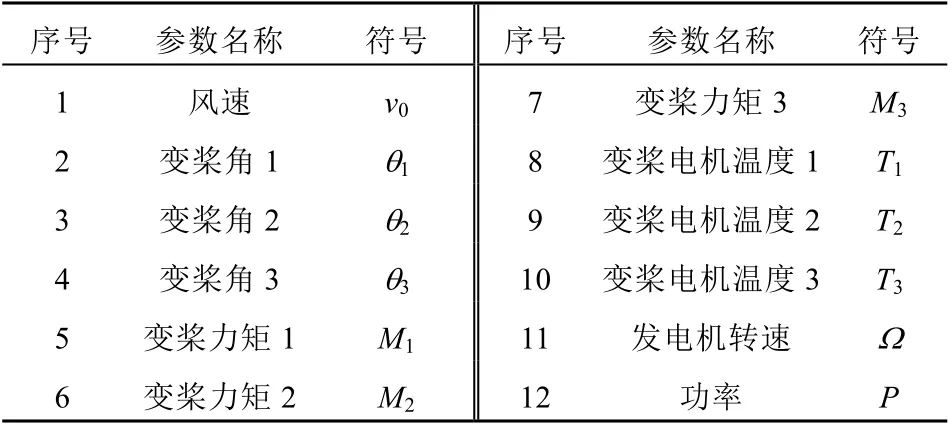
表1 风机变桨系统监测参数Tab. 1 Monitoring parameters of wind turbine pitch system

3.2 变桨异常预测分析

风力机的3个叶片具有3组独立同步的变桨驱动装置。当风速突然变化，叶片需要频繁改变桨距角时，3个桨距驱动器的同步动作失效往往导致多个故障同时发生。表2记录了2017年1月1日发生的多次报警记录。经证实，主要原因是3个叶片的俯仰动作经后期维护后不同步。这种故障是由典型的机械磨损引起的，其故障特征将隐藏在SCADA数据中。因此，所监测的相关信号可以表示为

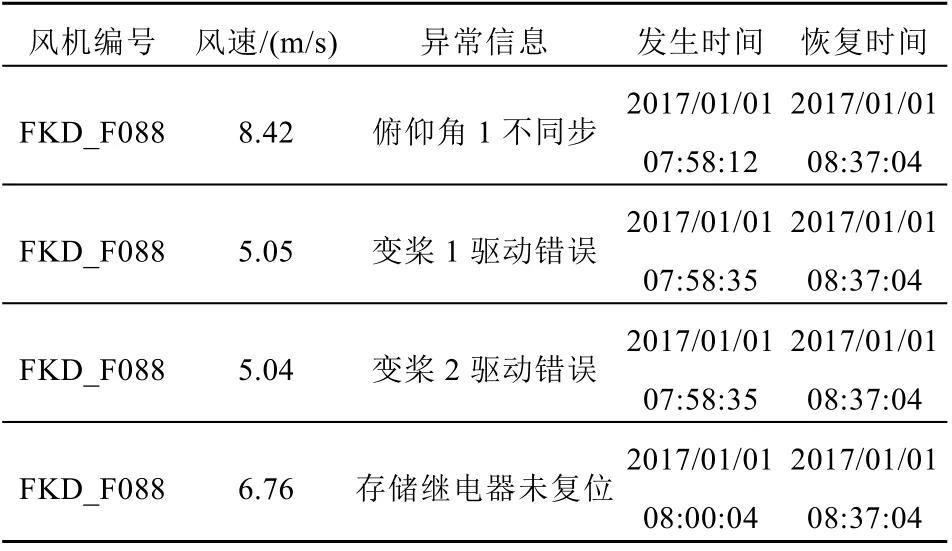
表2 风机变桨系统故障报警记录Tab. 2 Fault alarm record of wind turbine pitch system

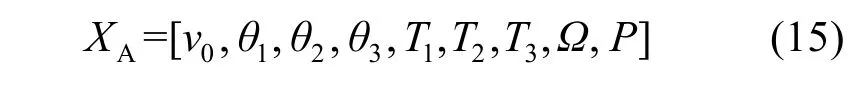
使用数据集XA训练DSWNN、DBN和DNN模型，然后使用记录的故障SCADA数据计算预测的均方误差，结果见图6。

从图6(c)可以看出，在时间t3之前，DSWNN获得的预测误差在自适应阈值范围内波动。但t3后，误差接近其上限，然后逐渐超过其上限。根据表2报警记录，第一个名为“俯仰角1不同步”的故障发生在07:58:12。这意味着DSWNN可以在实际停机时间前大约3 h检测到异常，从而为俯仰系统的维护提供了足够的时间。对比图6(a)和图6(b)可知，DNN和DBN模型分别可以提前1.1 h和2.3 h预测出故障，均比本文所提出的DSWNN模型预测时间短。此外，DSWNN模型的计算误差在3种模型中也最小，说明DSWNN模型可以从正常的SCADA数据中提取更充分的动态特征。因此，一方面，用DSWNN模型来描述俯仰系统的动态特性更为准确，且可更早地检测出早期故障。另一方面，自适应阈值可以有效地跟踪预测误差，以提高预测模型的适应性，为系统减少误报和漏报提供了更准确的判断依据。

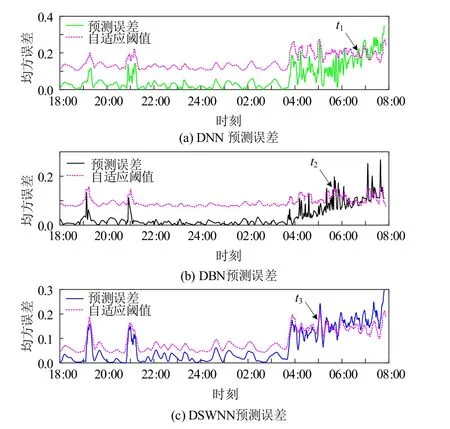
图6 故障预测误差Fig. 6 Fault prediction error

3.3 变桨故障分类性能比较

为了验证所提出的多故障分类方法的准确性，根据SCADA系统的实际报警信息，选取了9个典型或频繁的基本故障作为分类目标。表3列出了具体的故障，其中F1～F9表示9个故障报警，F10表示无故障状态。同样，采用DBN和DNN作为比较模型，3个模型采用相同的网络结构：1）输入神经元数量为12个，对应于表1中描述的12维参数；2）输出神经元数量为10个，分别对应于表3中的10个分类；3）3种模型均选择5个隐含层，每层30个神经元。具体而言，DSWNN模型在预训练过程中有5个RBM，小世界转换过程中的概率设为p=0.1。与DSWNN相比，DBN模型没有小世界转换的过程，它只包括2个过程：预训练和微调。DNN模型是一种标准的多层前向神经网络，其训练过程遵循误差反向传播原理。

表3 故障列表Tab. 3 Fault list

在数据准备方面，将实验数据分为20 000段训练数据和6 000段验证数据。此外，每个故障类别都包含一定数量的故障数据，数据分布如表4所示。值得注意的是，提供的所有数据片段都是根据相应的故障类型进行标记的。在模型训练过程中，DSWNN和DBN首先由去掉标签的数据片段进行预训练，然后用这些标签的数据片段进行微调。简单地说，神经网络模型使用所有标记数据进行训练和验证，这些训练和验证是在有监督的环境下进行的。

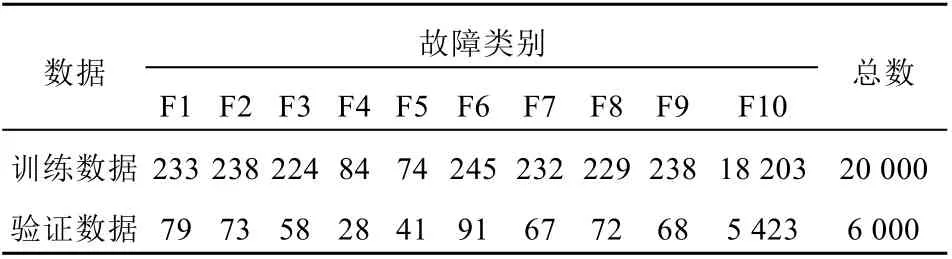
表4 实验数据的分配Tab. 4 Confusion information of the experimental data

图7给出了3个模型的分类精度。通过与混淆矩阵中所示的错误分类条件比较，神经网络模型可以很容易地判断F3、F5、F6和F8的错误，因为这些真实的否定会导致严重的后果。F3、F5为电气故障，其发生具有较强的随机性和偶然性。F6和F8与桨距角有关，而桨距角应该由风速、风力、桨距角编码器和叶根扭矩等监测，这些故障的原因是随机风速对叶片的影响很大。诊断上述故障的基本要求是，所使用的分类算法应具有从多个运行数据中挖掘隐含特征的能力。

图7 3种神经网络对10种故障分类精度的比较Fig. 7 Comparison of three neural networks in classification accuracy of 10 types of faults

然而，这正是神经网络模型所缺乏的，因为它的网络参数是由随机初始化产生的，没有任何理论基础。众所周知，参数直接影响分类结果。DSWNN和DBN模型使用了预训练来获得更好的网络参数，并且它们对所有故障的分类精度都比DNN模型显示出更好的性能(见图7(b)和7(c))。但故障F4和F5的诊断准确率也有所下降，这可能是由训练数据中缺乏故障数据所致。

此外，还同时记录了3个模型在训练过程中的全局变化误差，如图8所示。从图中可以看出，DSWNN、DBN和DNN的收敛时间分别为255、210、168 s。DSWNN的计算时间最长，这是因为它在预训练和微调之间有一个小世界转换过程。在0～110 s间隔内，DSWNN和DBN的训练误差几乎达到阶段稳定，这是因为网络处于训练前阶段，其多个RBM达到了能量守恒。在110～130 s范围内，DSWNN和DBN由无监督训练变为有监督训练，训练误差突然减小，出现新的低收敛值。在124 s时，DSWNN的训练误差在短时间内增加，这是由小世界转换后网络结构中增加的边的附加权值引起的。DSWNN重新跟踪随机的新添加边，导致短期误差增加。

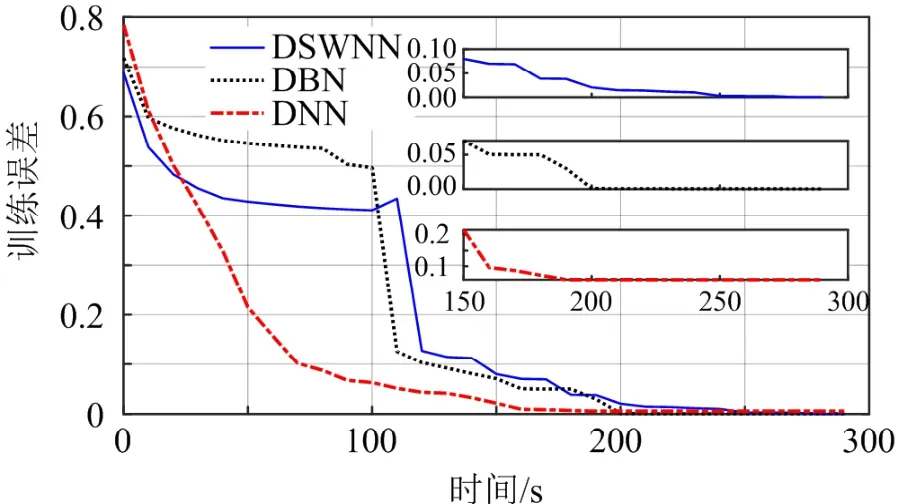
图8 DSWNN、DBN和DNN的训练误差Fig. 8 Training error of DSWNN, DBN, and DNN

4 结论

提出了一种基于无监督学习的风电机组早期异常检测DSWNN模型。DSWNN模型是深度自编码网络和小世界神经网络的有效结合，可以更准确地模拟风力发电机的动态行为。基于实际案例的仿真分析得出如下结论：

1）自适应阈值能够有效地跟踪预测误差，减少误报。因此，所提出的基于极值理论的自适应阈值方法可以应用于风电机组的实时监测，减少风速波动和外界干扰对风电机组异常检测的影响。

2）与DBN和DNN算法相比，DSWNN模型具有更小、更准确的预测误差，证明了DSWNN模型具有深度网络特征和更好的学习能力。

3）结合DSWNN模型和自适应阈值，能够提前3 h预测变桨距系统故障，可用于后续的风电机组异常检测和故障诊断。