炉膛声学层析测温探头分布方式研究

张立峰，苗雨

（华北电力大学自动化系，河北省 保定市 071003）

0 引言

温度场分布信息可反映锅炉炉膛内部燃烧状态，帮助机组控制人员制定合理的控制策略，对确保发电系统稳定运行、提高机组燃烧效率具有重要意义。因此，需对炉膛内温度分布进行实时及准确的监测[1]。

声学层析成像(acoustic tomography，AT)具有非侵入、测温范围广、适用于大尺度空间测量等优点，是极具发展前景的温度分布可视化测量技术。声学测温法是一种非接触式的声测热技术，克服了传统接触式物理测温方法的缺点。该方法通过推导波动方程，建立声波传播速度与被测介质温度之间的单值函数关系。在正问题中，当超声波“透射”被测介质后，测量超声飞行时间(time-of-flight，TOF)数据，再通过求解逆问题获取声波传播速度，最终实现温度分布测量[2-4]，该技术广泛应用于生物健康及工业生产检测与炉膛温度分布监测[5-6]。

国内外学者对声学测温进行了大量相关研究。Holstein等[4]将被测区域分为粗网格并在其周围布置超声波探头以获取TOF数据，由于网格划分较粗，导致重建结果仅能反映热点存在及相应的温度特征；Barth等[7]在位于1.3 m×1.0 m×1.2 m的被测区域内布置16个声波传感器，并采用同步迭代算法实现了室内空间的温度分布和速度分布同时测量；王善辉等[8]对声学传感器列阵的仿真设计，提高了声学层析成像系统的性能，并获得了较高的重建精度。

探头分布将直接影响有效声波传播路径的数量及TOF数据的测量[9]，然而关于声学层析测温的超声波探头分布方式的研究鲜有报道。

本文针对目前文献报道较多的8、12及16探头声学层析测温系统，研究了4面及4角式分布，对3种典型温度场采用Tikhonov正则化和局部加权回归法进行仿真重建，根据不同分布方式划分不同区域，在均匀空气及烟气分布下分别进行了仿真研究，最终确定了最优探头分布方式。

1 声学层析测温原理

1.1 超声测温原理

超声波在介质中的传播速度随介质温度的变化而变化。在理想气体中，声波的传播速度与介质温度的关系[10]为

式中：C为超声波在气体介质的传播速度；M为气体分子质量；γ为气体定压热容与定容热容之比；R为气体普适常量；T为介质温度。

AT温度分布测量原理是在被测区域边缘处安装一定数目的声波探头对，当一个声波探头发出的信号被另一个检测到时，声波传播路径d为已知量，通过测量出声波在2个探头对之间的TOF数据，再利用声波传播速度C与介质温度T之间的单值函数关系，即可确定该收发器对所在路径的气体介质温度T[11]：

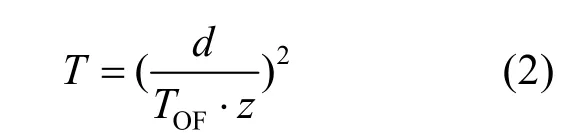
式中：TOF为声波飞行时间；z为烟道混合气体常数。在进行AT测量时，首先需要获取声波在每一条传播路径上的TOF数据，再经计算后得到其气体介质温度T。

结合距离公式，超声波从发射器到接收器的传播时间[12]可表示为

式中l为超声波发射器与接收器之间的路径。

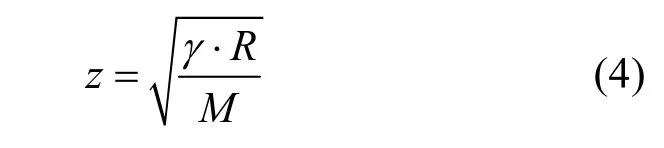
当气体环境确定时，式(4)中γ、R、M即为已知量，可将其视为常量z，当气体环境为空气时，z常取20.05[12]。

实际运行中炉膛内部气体成分十分复杂，其主要为CO2、H2O、O2及CO等。随着炉膛燃烧的进行，各种气体成分比例也在不断变化[13]，因此需要对气体常数z进行修正。在式(4)中气体分子质量M的表达式为

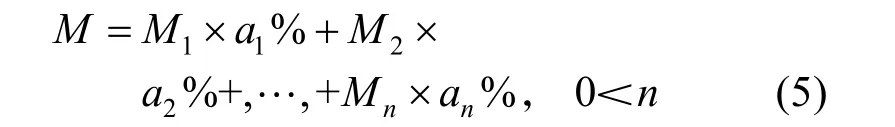
式中：ai(i=1,2,…,n)为第i种气体的体积百分比；Mi(i=1,2,…,n)为第i种气体的分子质量。因为气体分子质量时刻改变，根据常见运行条件将烟道混合气体常数z修正为19.08[14]，并在后续仿真研究中进行了分析。

基于超声法重建温度场在本质上属于逆问题的范畴。在温度重建过程中，需要对被测区域进行网格离散化。首先将温度场划分为n×n个小区域(像素)，每个小区域的温度tj不同，超声波在该区域的传播速度vj也不同，超声波在每一条路径k总的传播时间TOFk为其在各个小区域内传播时间之和，如果预先求出每一条声波路径穿过每个像素的长度wij，就可以通过数值计算求出其在每个小区域内的平均速度vj，假设每个网格内的速度近似相同，进而求出每个网格的温度tj。用矩阵的形式表达为

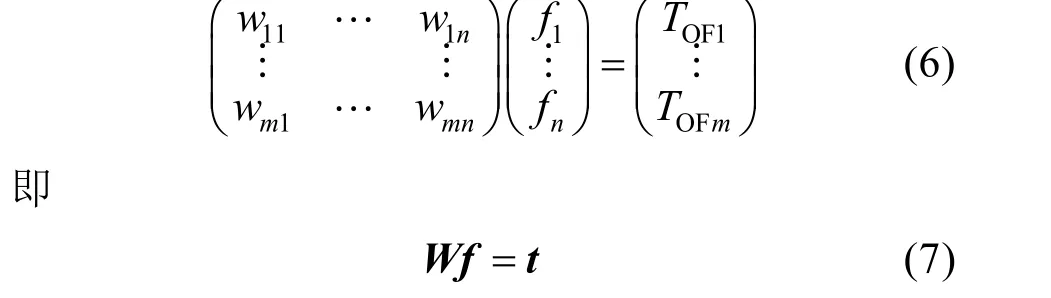
式中：fi为第i个网格的真实声速vj的倒数，即慢度；W为距离系数矩阵；f为声速系数矩阵；t为超声传播时间系数矩阵。

1.2 温度场重建算法

正则化化方法是处理这类问题的有效手段，已经成功地解决了许多不适定问题[15]。Tikhonov正则化是处理不适定问题的另一种解决方法，该方法由前苏联学者Tikhonov提出，对基于最小二乘原理的广义逆运算方法进行了改进，通过正则化调整，用满秩矩阵ATA+αI来代替奇异矩阵ATA，将不适定问题转化为适定问题，使病态问题也能得到唯一解[16]。

其中心思想是保证数据拟合的前提下，最小化目标函数，即

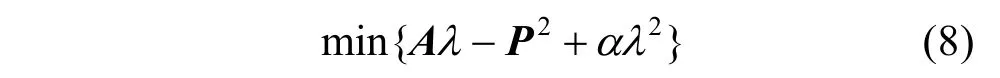
也就等价于求解ATA+αλ=ATP，得到最小二乘解为

式中：α是正则化参数，α过小时不能很好地抑制噪声，而α过大时会丢失高频分量而使重建图像模糊，本次仿真中α取值为0.000 1。

直接采用Tikhonov正则化用于温度场重建时，效果并不理想[17]。因此，先通过Tikhonov正则化得到粗网格下的温度分布矩阵T，再通过局部加权回归法进行预测得到细化后的温度分布。局部加权回归是一种非参数学习算法，对于一个确定的询问点x，都要进行一次局部加权回归，求得相应的θ，即

式中：x为预测点；x(i)为训练样本点，如果|x(i)-x|较小，那么权值接近1，反之接近0；τ为波长函数，用于控制权重的变化幅度。

2 探头分布方案及温度场重建

2.1 探头分布方案

仿真区域为10 m×10 m正方形，AT重建精度不仅受到探头布置的影响，亦受网格划分数目的影响[18]。在AT重建过程中，需将测量区域划分成一定数目的离散网格后再进行重建。采用最小二乘法重建温度场，该算法要求声波传播路径数大于被测区域离散网格数[19]。理论上，网格越多，重建质量越好，但过多的网格将导致声波未能穿过大量的网格，尤其在边缘区域，增加了逆问题的求解难度。因此本文先选择探头数目，再选择探头分布方式，最后确定网格划分数目。

目前使用较多的声学测温系统为8、12及16探头，本文研究了这3种探头数目下的4面及4角共6种分布方式，4面分布探头不布置在4个角上，而4角分布有部分探头布置在角上，如图1所示。

图1 6种探头分布Fig. 1 Six probe distributions

图1(a)表示8探头4角式分布，被测区域划分为4×4，共有16条有效传播路径；图1(b)表示8探头4面式分布，被测区域划分为4×4，共有24条有效传播路径；图1(c)表示12探头4角式分布，被测区域划分为6×6，共有42条有效传播路径；图1(d)表示12探头4面式分布，被测区域划分为7×7，共有54条有效传播路径；图1(e)表示16探头4角式分布，被测区域划分为9×9，共有80条有效传播路径；图1(f)表示16探头4面式分布，被测区域划分为10×10，共有96条有效传播路径，这6种分布后文分别简称为a、b、c、d、e、f分布。

若传播路径与网格剖分线重合，将导致有效传播路径缺失，从而影响反问题的欠定性，为减少重合情况，将每个探头以坐标中心点为中心旋转适当角度，使有效传播路径与网格线分离。当超声波测温系统确定后，每个传感器的位置也随之确定，即可用一定的算法确定所需的系数矩阵W，然后通过相应的数值算法重建被测温度场。

2.2 温度场模型

本文采用单峰偏置、双峰对称、4峰3种典型的峰型温度场进行仿真重建，仿真环境设为气体常数为20.05的稳定环境，干扰噪声为0，温度场模型分布如式(13)—(15)所示。

单峰偏置温度场Z的函数表达式为

3种温度场对应的函数图如图2所示。

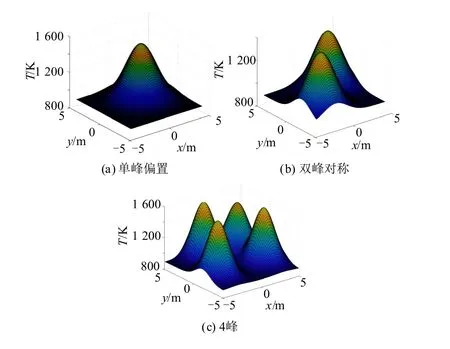
图2 温度场函数图Fig. 2 Temperature field function diagram

为定量评价6种探头分布方式图像重建的质量，本文采用均方根误差Emse及相关系数Re两个误差评价指标，其计算公式分别为：

根据式(15)和(16)可知，Emse越接近0，则重建精度越高；eR越接近1，则重建效果更接近模型。在对比中2个评价指标趋势不同，因此定义综合评价指标：

式中Kem越大，则重建效果越好。

2.3 温度场重建结果

单峰偏置温度模型的重建结果如图3所示。由图3可见，6种分布方式的重建效果都体现出单峰偏置温度场的分布特点，其重建误差如表1所示。

图3 单峰偏置温度场重建结果Fig. 3 Single-peak bias temperature field reconstruction results

从表1的结果看，采用分布方式e(4角16探头)对单峰偏置温度场的重建效果更好；采用分布方式d(4面12探头)对单峰偏置温度场的重建效果较差。当探头数目为8个时，采用4面或4角式对重建结果的影响不大。

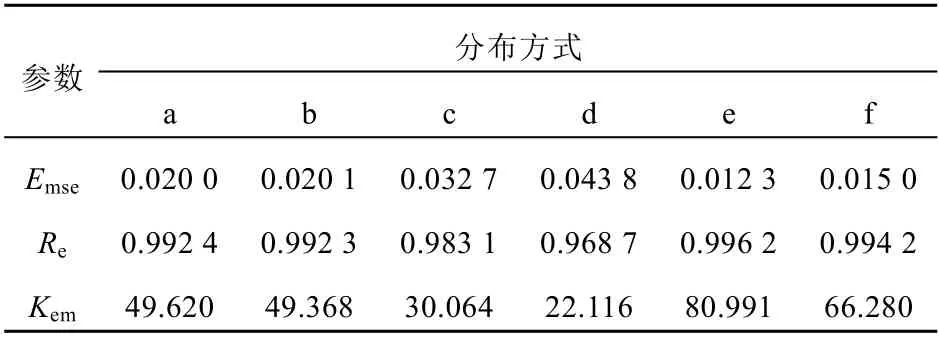
表1 单峰偏置温度分布重建误差Tab. 1 Reconstruction error of single-peak bias temperature distribution

双峰对称温度模型的重建结果如图4所示。由图4可见，6种分布方式均可重建出双峰对称温度场的峰型特征与位置特征，其重建误差如表2所示。

图4 双峰对称温度场重建结果Fig. 4 Twin-peak symmetrical temperature field reconstruction results

由表2可以看出，对于Emse和Re而言，分布方式f(4面16探头)均优于其他分布方式；对于综合指标Kem，分布方式f的值最大。

表2 双峰对称温度分布重建误差Tab. 2 Reconstruction error of double-peak symmetrical temperature distribution

4峰温度模型的重建结果如图5所示。由图5可见，从峰型特征上分析，4角12探头、4角16探头和4面16探头均可以体现出4峰，8探头基本可体现出4峰，但在完整度方面有所欠缺，其重建误差如表3所示。

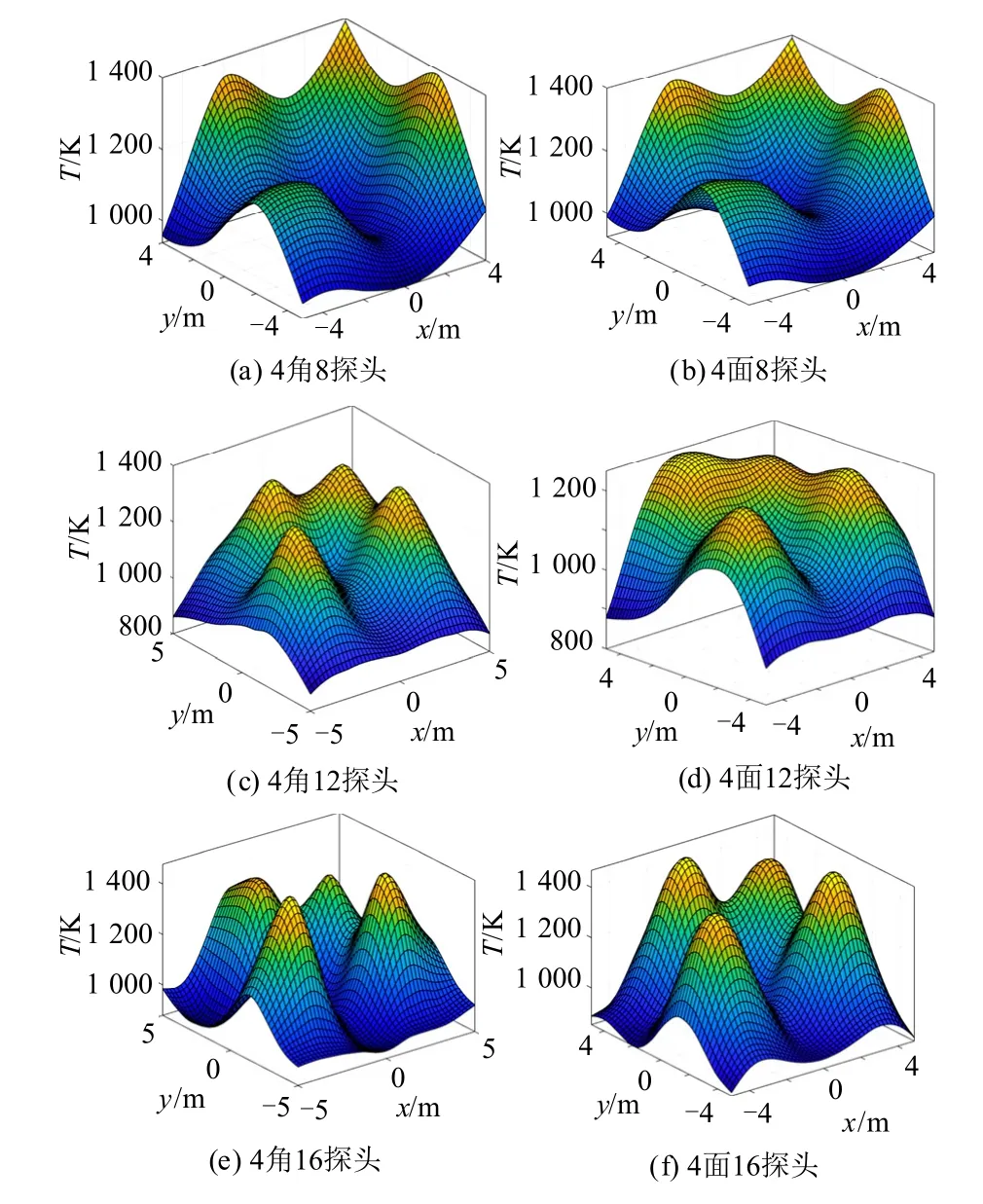
图5 4峰温度场重建结果Fig. 5 Four-peak temperature field reconstruction results

从表3可以看出，分布方式f(4面16探头)的重建结果Emse可达0.039 6，远低于其他分布方式；eR可达0.974 6，既保证了分布特征又保证了相似度，重建精度明显高于其他分布方式。

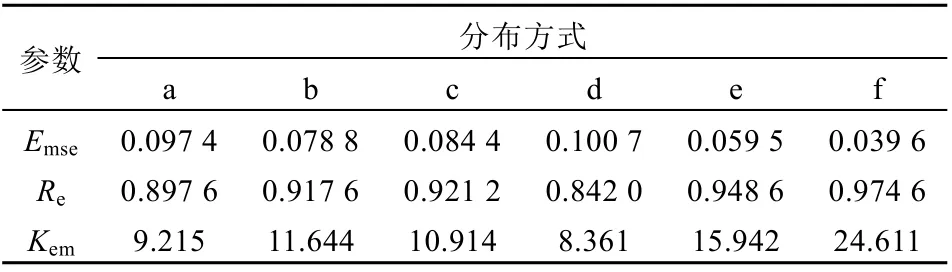
表3 4峰温度分布重建误差Tab. 3 Four-peak temperature distribution reconstruction error

2.4 结果分析及修正

表4 均匀空气分布下的综合指标均值Tab. 4 Mean value of comprehensive index under uniform air distribution

表5 烟气分布下的综合指标均值Tab. 5 Mean value of comprehensive index under flue gas distribution

3 结论

采用4面与4角式2种分布方式，结合8、12和16三种数目探头的分布方案，分别对单峰偏置、双峰对称和4峰3种典型温度场进行重建，仿真结果表明：

1）4面16探头分布对多种温度场的综合重建质量高于其他探头分布方式；

2）若现场无法布置16探头时，在模型不复杂的情况下，优先选择8探头，4面或4角式分布对8探头重建质量影响较小；当采用12探头时，4角分布的重建质量高于4面分布，应优先选择4角分布。