基于尖点突变的城市交通状态演化研究

邵子怡，张林,2，吴昊

(1.华北理工大学 建筑工程学院，河北 唐山 063210；2.中美城市交通研究中心，河北 唐山 063000)

随着我国经济的高速发展和城市化进程的加快，交通拥堵已经成为制约城市发展的一大顽疾。道路交通系统是一个复杂的非线性系统，实测交通流数据在拥堵发生时刻会出现非连续的“突变”现象。此现象是在交通畅通状态到交通拥挤状态的过渡时期形成的。而传统的交通流理论模型：Underwood指数模型、Greenshield线性模型、Greenberg对数模型，均为建立在二维平面基础上的3个参数模型。这些模型无法解释在交通流数据中出现的“突变”现象。法国数学家Thom在20世纪70年代基于奇点理论和稳定性理论建立了7种突变模型，并用于研究不连续变化的现象。1978年Dendrinos是第一个将突变理论应用到交通流这一领域的人，他将二维的突变模型用来描述速度-流量关系曲线[1]。另一个模型是由Navin于1986年提出的，他认为三维的突变模型适用于描述3个变量[2]。张亚平和张起森对实测数据进行变换之后，应用尖点突变去描述交通流3个参数的关系，并验证了尖点突变应用于交通流预测的可行性[3]。姜璐等总结了初等突变理论在社会科学中的2种应用途径并以燕尾突变为例，给出了具体的分析步骤和突变特点[4]。YiShui等分析在快速路上的交通拥堵与交通瓶颈的关系，并得出交通运行状态会在较短时间发生突变并导致拥堵的结论[5]。上述研究只是将实例数据做了简单特征分析，预测未来交通流，但未采用尖点突变理论做系统的关联阐述，并对交通由畅通流-拥堵流的演变过程进行分析研究。该研究从交通流的实际交通数据出发，对交通流作拥堵分析，并将其与尖点突变理论结合，从流量、占有率、速度3个参数对城市交通状态的演化做详尽分析。

1交通流的拥堵特性

1.1 数据样本分析

该项研究利用无人机航拍的方式对唐山市路北区西山道与学院路交叉口于2019年11月21日和2019年11月22日的6:30～8:00早高峰时段进行车流量采集。北新道与建设路均为双向8车道，统计时间间隔为5 min，分别对流量、速度和占有率进行统计，并对数据进行了相应的预处理，剔除了冗余、无效的数据。表1所示为高峰时段部分流量、速度、占有率的统计情况。

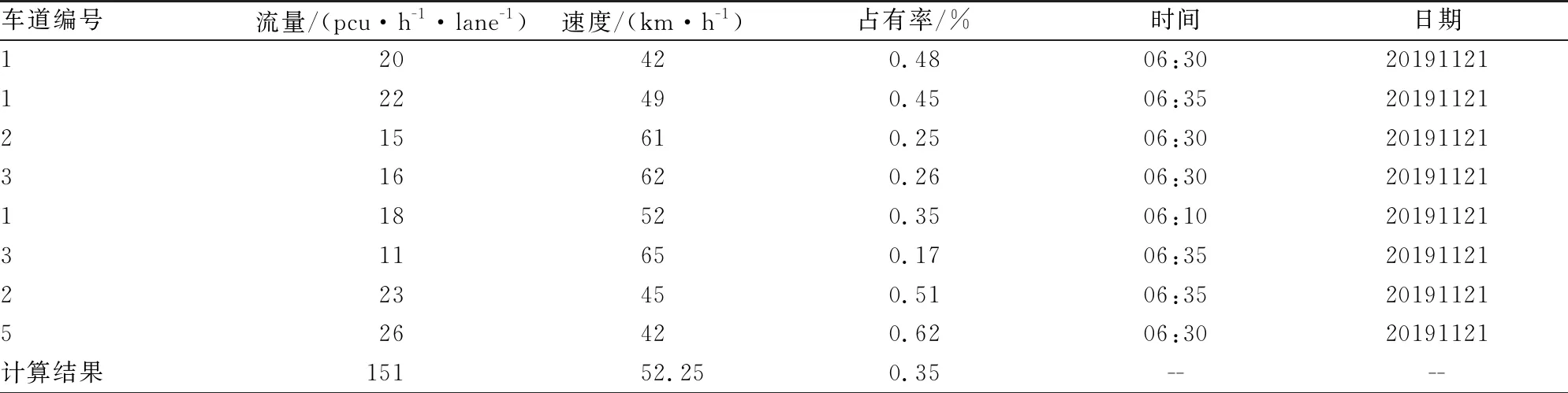
表1 数据样本示例

1.2 交通流拥堵分析

根据交通拥堵发生的频率可以将其分为常发性拥堵和偶发性拥堵，常发性拥堵在设计学因素的影响下可以分为结构性拥堵和非结构性拥堵。交通道路设计结构性缺陷(分段限速、车道变窄等)不明显存在的情况下导致的常发性拥堵，其主要原因是交通需求与交通供给不平衡。为了更形象、直观地描述交通流三项参数与尖点突变之间的关系，绘制出占有率-流量、流量-速度和占有率-速度之间的关系图。

图1所示是占有率-流量关系的二维图。观察图1可得，交通状态在非拥堵状态和拥堵状态比较集中，而非拥堵和拥堵状态的衔接是不连续的，表现为交通状态的突跳性。由此可见，交通状态突跳性的变化与尖点突变理论的突变性是一致的。

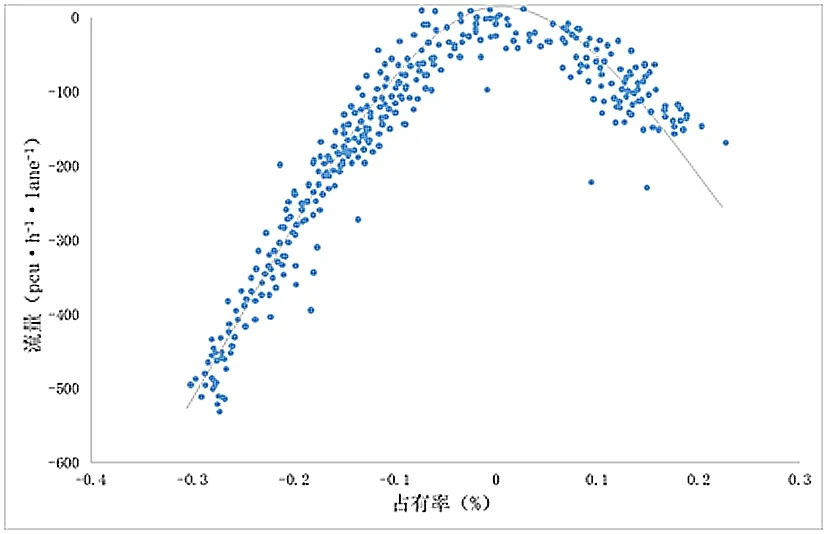
图1 占有率-流量关系图

图2所示是流量-速度关系的二维图。观察图2可得，同一流量值可能对应2个速度值，同一流量值的上半部分对应的是拥堵状态对应的速度，下半部分是非拥堵状态对应的速度，这体现了交通状态的多态性。由此可见，交通状态的多态性与尖点突变理论的多模态性是一致的。

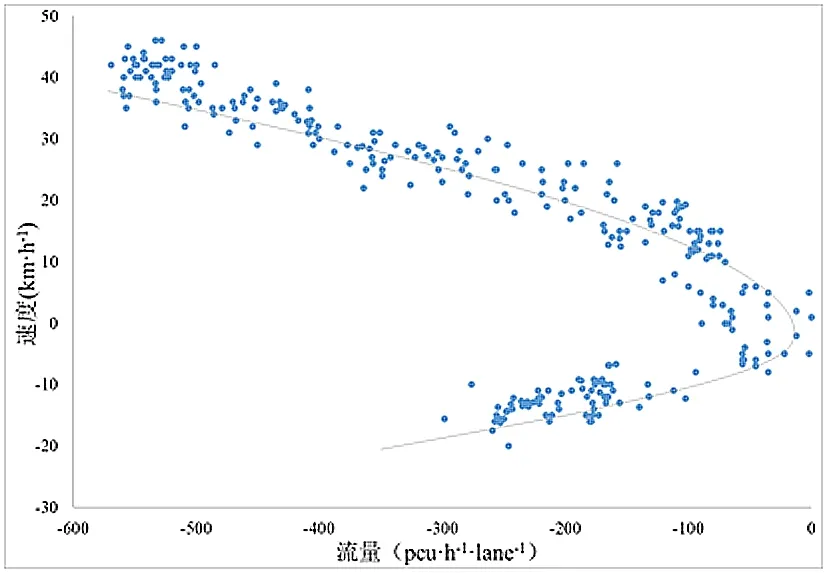
图2 流量-速度关系图

图3所示是占有率-速度关系的二维图。观察图3可得，该区域的数值较为集中，是因为驾驶员具有较强的时间概念以减少道路上的延误。在原点周围占有率-速度出现了明显的跳跃变化，由非拥堵的平衡状态跳跃到拥堵的平衡状态，这体现了交通状态的不可达性，与尖点突变理论中的不可达性是一致的。

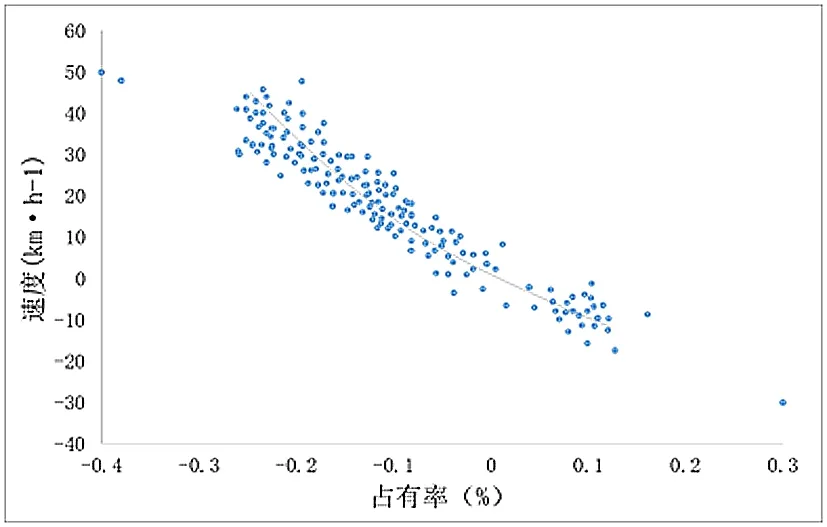
图3 占有率-速度关系图

通过对3个参数之间关系的分析，表明交通状态与尖点突变理论有着相似的特征，因此利用尖点突变理论研究交通拥堵的状态演化具有一定的理论依据。

2突变理论

法国数学家Thom于1972年在《结构稳定性和形态发生学》一书中关于突变原理问题进行阐述，标志着突变理论的正式诞生。突变理论是通过建立势函数，探究突变临界点以描述系统发生突变时所发生的潜在规律。该理论表明，某个因素的持续变化可能会导致整个系统的态势发生突然改变。量变造成质变，事物的质变关键在于中间态是否稳定，反之则会发生突变。

突变理论包含2个参数，分别是状态变量和控制变量。状态变量是系统中任何时刻的状态都由n个给定的变量确定(n有取值范围)。控制变量则是系统中受到m个变量的控制。控制变量就是影响系统形态的重要因素。在突变理论中，状态参数与控制参数的数量分别控制在2个和4个的初等突变函数有以下7类：折迭型、尖点型、燕尾型、蝴蝶型、双曲型、椭圆型、抛物型。针对不同系统，尤其是存在突变情况的系统，在对系统进行准确分析后，可以对状态变量与控制变量的个数进行确定，再次从以上7种初等突变函数中选择一类适合的模型，从中总结该系统的演化特征。

突变理论的特性主要用来分析微分动力学体系中状态的跳跃变化，以及在光滑动力学中平衡态的分歧问题。其特性体现在以下几个方面：

(1)突变性

对于Maxwell约定而言，系统总是转移到使它的势全局最小的平衡位置(即极小值中的最小值)，其势的变化是连续的，但是导数变化是不连续的；对于理想延迟约定而言，系统在控制参数的变化时，由原来的平衡位置跳跃到局部极小或者全局极小位置，其势的变化是不连续的。在交通系统中，势函数的值随着交通流量的增加而增加，若交通流量突然发生变化，超过突变临界点，势函数的数值会瞬间变小。

(2)不可达性

在系统中存在3种状态之间的转化，由稳定平衡态—不稳定平衡态—稳定平衡态，系统从稳定平衡态到达下一个稳定平衡态的过程中直接跳跃了不稳定平衡态，所以该不稳定的平衡状态是系统不能达到的状态。

(3)分歧性(发散性)

在系统中，状态变量是随着控制变量的变化而改变的。一般来说，控制变量的改变只会引起状态变量的微小变动，但此微小变动会使其处于突变的临界位置来回摇摆，则会导致极大改变。

(4)多模态性(双模态性)

对于系统本身来说，存在的状态可能是2个，也可能是多个，所以在改变参数时，系统才可能从一个稳定位置跃迁到下一个稳定位置，发生突变。在交通系统中，通畅和拥堵都是状态的表现形式。

(5)滞后性

突变的发生是与控制变量的方向有关的。当一个局部极小与另一个局部极小相互跳跃时，控制变量所对应的点是不断变化的，所以说当控制变量从不同方向进行改变时，发生的突变状况是有差异的。这种情况只存在于理想延迟约定，Maxwell约定中不存在滞后情况。

在选取模型进行分析时，可以考虑系统中存在的状态变量和控制变量的个数来建立合适的突变模型用于求解问题。假设系统的演化可以由一个状态变量和2个控制变量来描述，并且有明显的突变现象，则对平衡曲面的刻画就有式(1)所示的形式。

x2+ux+v=0

(1)

由Siersma算法[6]可得，该系统平衡曲面方程可化为式(2)所示。

(2)

与折迭突变的平衡曲面为同一类型。

x2+v=0

(3)

由此可得，刻画满足式(1)的系统只需要1个控制变量。因此，描述上述2个控制变量和1个状态变量系统的平衡曲面应为式(4)所示。

4x3+2ux+v=0

(4)

在交通系统中，将对速度、流量、占有率3个变量进行分析，因此，将速度作为状态变量，流量、占有率作为控制变量，此时应该选择1个状态变量和2个控制变量的尖点突变模型。

3基于尖点突变的交通状态演化研究

3.1 基于尖点突变的交通状态演化模型建立

尖点突变势函数为：

F(x)=ax4+bαx2+cβx

(5)

对式(5)求导得到的曲面即为突变流形：

4ax3+2bαx2+cβ=0

(6)

12ax2+2bα=0

(7)

分叉集应同时满足突变流形方程与势函数的二阶导数方程，即分叉集为突变流形的皱褶在α-β平面上的投影： 8bα3+27ac2β2=0

(8)

其中:

x——状态变量：速度，km·h-1；

α——控制变量：流量，pcu ·h-1·lane-1；

β——状态变量：车道占有率，%；

a、b、c——参数。

3.2 基于尖点突变的交通状态演化模型求解

为满足Maxwell约定，尖点突变理论应用于交通流3个参数的分析中需进行一些变换。初次变换为坐标平移，经过坐标平移之后，α-β平面中的α轴与Maxwell约定中的垂直面重合并作为区分交通流中拥挤状态与非拥挤状态的界限，满足分叉的特性(如图4所示)。

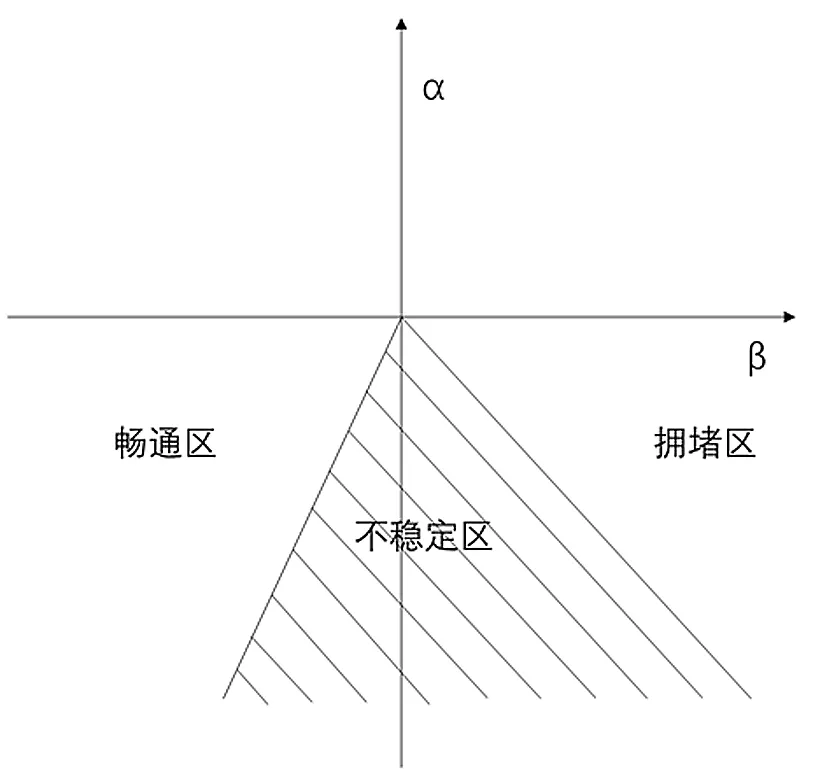
图4 尖点突变分叉集

(1)坐标平移

(9)

其中：

xm——最大流量时最大车道占有率对应的速度，km·h-1；

αm——最大流量，pcu ·h-1·lane-1；

βm——最大流量对应最大车道占有率，%

(2)坐标旋转

坐标平移后，需要对α轴和β轴进行旋转，与Maxwell约定的垂直面重叠，因此可将α轴定义为区分非拥挤和拥挤状态的界限，即：

(10)

其中：

m——图形因子：是αm与βm的比值；

θ——旋转角度，°。

经数据处理后，方程可写为：

(11)

4 城市交通状态演化分析

突变理论的应用最早的特征是Zeeman提出的“狗受到威胁时的反应”。“狗受到威胁时的反应”被假设为一个系统(比如一条狗)在遇到不同因素的情况下做出的不同反应(比如狗的咆哮、追赶)。将狗的反应定义为状态因素，愤怒和恐惧定义为控制因素。图5表示狗由正常到受到威胁时的若干种行为可能。

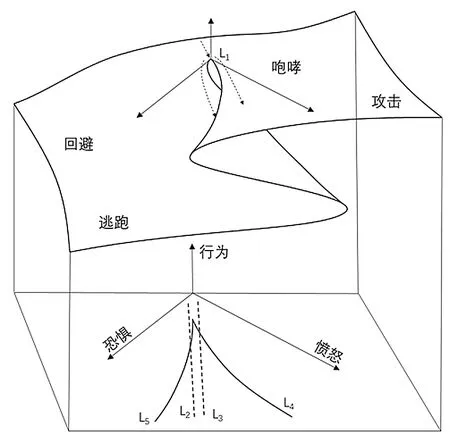
图5 狗受到威胁时的反应

路径L1：此路径表示在愤怒和恐惧2种控制因素同时增加时，可能会造成的2种不同结果分别是畏缩不前(路径L2)和产生攻击行为(路径L3)。

路径L4：随着愤怒增加，狗的回避突然转变为攻击。当狗受到外界刺激而被激怒时，通常会保持一段时间的畏缩不前，而后突然变为攻击状态。一旦出于攻击状态，即使愤怒减小也会维持现状。

路径L5：此时狗处于攻击状态，随着恐惧的增加，攻击状态会突变为畏缩不前。一旦处于畏缩不前的状态，即使恐惧减少也会维持现状。

“狗受到威胁时的反应”与城市交通拥堵的演化相似(如图6所示)。在城市道路，伴随上班高峰期的到来，车量逐渐增加，相应路段的车辆占有率也会随之增加。与此同时，交通路径会按照路径L4-L5从畅通状态过渡到拥堵状态；若当交通流处于畅通平衡态，突然有交通事故的发生，则会导致路段占有率激增，路段通行能力大大减小，流量减小，此时交通流会按照L3-L2从畅通状态突变为拥堵状态。为预防城市道路交通拥堵的发生，提出以下建议与措施：(1)对城市道路的功能和配套设施采取科学的评估方法，使其符合当前城市道路系统的要求；(2)对道路等级进行重新规划，根据周边配套设施配置合理的道路等级比重，做到运行效率高又考虑到交通流的分流效果，最大限度的发挥道路资源；(3)通过合理的渠化设计在原有道路条件的基础上增加道路通行能力；(4)在有效避免交通事故发生的前提下，也可提高瓶颈路口的通行能力，缓解交通拥堵的传播。

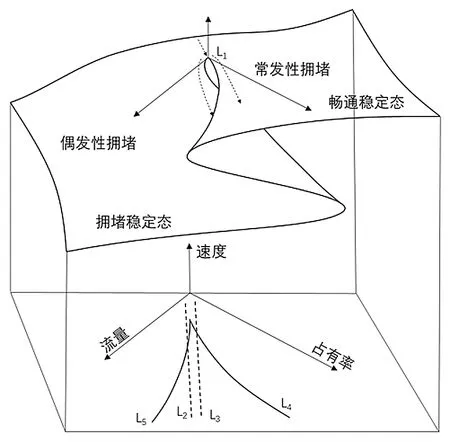
图6 城市交通流状态演化

5结论

(1)阐述了道路系统在运行过程中具有的基本特征和运行规律，提出了基于尖点突变的城市交通状态演化模型。通过对势函数和分叉集的讨论分析，对交通状态进行划分。

(2)结合“狗受到威胁时的反应”的分析对交通状态的演化过程进行描述。发现城市道路交通状态会存在不稳定的突变特性。

(3)城市道路发生交通拥堵现象时，为更好地实施交通控制和拥堵疏导应从多角度出发，考虑交通流的空间特性，利用尖点突变曲面判断城市道路交通状态突变的关键节点，根据拥堵形成的消散特征实施有效、合理的疏导措施。