基于Python的AHP-熵权法的信贷风险分析模型

王 若 雨

(哈尔滨工业大学(威海) 信息科学与工程学院，山东 威海 264209)

截至目前，中国有2 000多万中小微企业法人和6 000多万个体工商户，这些中小微企业占市场主体的90%以上，贡献了全国80%的就业、70%左右的专利发明权、60%以上的GDP和50%以上的税收。中小微企业已经成为国家产业升级的新生力量和吸纳就业的重要载体，是社会经济发展的主力军。但中小微企业也面临诸多先天不足，如规模相对较小、可抵押的资产较少、资金短缺和融资困难等。总之，中小微企业的可持续发展能力还较弱，需要社会各方面，特别是金融资金方面的扶持助力[1]。加强银行信贷对优质中小微企业的支持力度，同时降低银行信贷风险已成为业界亟待探讨解决的课题。该文基于Python语言程序，针对规模相对较小且缺少抵押资产的中小微企业，结合其实际经营运行特点，运用AHP-熵权法建立了信贷风险分析模型，以期指导实际信贷工作。

一、AHP-熵值法信贷风险分析及Python程序

信贷决策分析是运用构建的风险识别指标体系对风险进行综合评估的过程。风险识别指标体系是由一系列相互联系的指标构成的组合，由于各指标之间存在差异，且每一项识别指标在整体评价中的相对重要程度也不相同，为保证综合评价的客观性，须给每项指标赋予一定的权重。目前,研究指标赋权的方法主要有两大类，即主观赋权法和客观赋权法。

主观赋权法方面，比较典型的是层次分析法，简称AHP，其由美国运筹学家萨蒂提出，对风险因素问题进行分层决策分析。AHP法将决策分析分成不同层次，明确各层所涉及的内容，构建层次比较判断矩阵，由专业分析人员对指标进行两两比较，并根据指标间的相对重要性进行定量描述，进而计算出指标的权重，再通过所有层次之间的总排序运算得到指标体系赋权重[2]。AHP法适用范围较广，特别是在风险分析方面优势明显。然而，AHP法依据评价者对指标重要性的认识来确定指标权重，容易受主观因素的影响，如个人学识、经验和习惯等。客观赋权法方面，熵值法比较有代表性。熵的概念由德国物理学家克劳修斯提出，可以较为准确地度量系统的无序程度。熵值法完全依靠指标样本观测值自身的信息来判断指标的有效性和重要性，受人为因素干扰较小，可以作出较为客观公正的评价。但该方法也有难以克服的缺点，如该法是根据指标所提供的信息量大小和相互关联程度来确定指标权重的，容易受样本观测值差异性与样本数量不足等因素的影响，造成客观赋权误差。

AHP-熵值法是层次分析法和熵值法的有机结合，它充分考虑了影响两种赋权方法的不利因素[3]，首先利用层次分析法计算出反映专家主观意志的主观权重，保证重要性指标所占权重较大，其次利用样本数据自身的信息对主观权重进行调整，如运用熵值法的差异性系数对层次分析法的权重进行修正，得出优化权重组合[4]。

Python是一种跨平台的、独立的大型计算机程序设计语言，由荷兰人吉多·范罗苏姆在20世纪90年代初开发，最初被设计用于编写自动化脚本，随着语言新功能的不断添加和版本的多次更新，开始日益广泛应用于独立的大型项目的开发分析。Python结合了解释性、编译性、互动性和面向对象的脚本语言，完全面向函数、模块、数字和字符串等对象，提供了丰富的API和工具，便于模块扩充。

AHP-熵值法信贷决策分析结合主客观多种因素，是一种多层次、多种类和多目标的参数指标评估体系。Python适应这一复杂分析需求，通过语言编程，形成海量数据分析决策模型，服务银行信贷决策[5]。

二、信贷风险分析模型的建立

基于Python的AHP-熵权法并结合实际情况量化分析企业信贷风险，进而确定对于这些企业的信贷策略。企业风险评估模型主要符号为：风险评价指数：σ，权重：ω，财务指标：D1，非财务指标：D2，偿债能力指标：E1，盈利能力指标：E2，发展能力指标：E3，信用评级信息：E4，违约信息：E5，利息保障倍数：F1，供求关系稳定性：F2，息税前利润：F3，经营利润率：F4，利润增长率：F5等。

企业风险评估模型是一个递阶层次结构，假定将其分为3个层级，共计选取18个指标进行分析(表1)[6]。

表1 风险评估模型指标

(一)确定企业风险评估指标

根据企业已有资料，计算确定其风险评估指标。针对规模相对较小且缺少抵押资产的中小微企业，结合银行通常作法，主要参考信贷政策、企业的交易票据信息和上下游企业的影响力分析信贷风险，确定信贷政策。

假定风险评估指标主要包含利息保障倍数、供求关系稳定性、息税前利润、经营利润率、利润增长率、信用评级和违约情况等7项。其中，息税前利润=收入总和-支出总和，利息保障倍数=息税前利润/利息费用，经营利润率=息税前利润/销售收入净额。供求关系稳定性通过各企业的销售交易规模确定，利息费用则根据各企业的信誉评级分类确定。

对非财务指标进行定性指标定量化，假定各指标对应量化值见表2。

表2 非财务指标量化值

对于极大型指标，令

使用极差变换法对所得指标数据进行无量纲化处理。

(二)企业风险评估指标赋权

运用层次分析法对二级财务指标的内部指标和三级盈利能力的内部指标进行赋权假定(表3～4)。

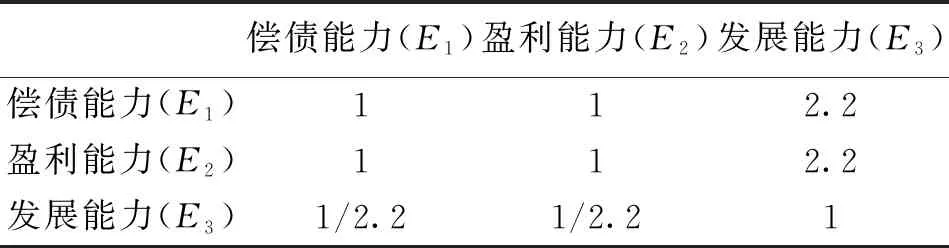
表3 二级财务指标的两两比较

把表3和表4中的数据用矩阵A1=(aij)3×3，A2=(aij)3×3表示，则

表4 三级盈利能力指标的两两比较

A1=(aij)3×3和A2=(aij)3×3为正互反矩阵，n阶正互反矩阵At=(aij)3×3，t=1,2的特点是aij>0,aij=1/aji,aii=1,i,j=1,2,…,n

由佩罗定理可知，两个矩阵各存在一个最大的特征值λtmax,t=1,2,λtmax所对应的特征向量为正向量，即AtXt=λtmaxXt。

将Xt(t=1,2)归一化(各个分量之和等于1)作为权向量Wt(t=1,2)，即Wt满足AtWt=λt maxWt。

利用Python可以求出最大特征值λ1max=3,λ2max=3,对应的特征向量经归一化得[7]

W1=[0.407，0.407，0.185]，W2=[0.5，0.2，0.3]

为保证权重准确性，对上述模型进行一致性检验，定义一致性指标

表5 平均随机一致性指标(RI)

在上述模型中，矩阵A1的一致性比率CR1=1.98×10-16<0.1，矩阵A2的一致性比率CR2=-1.98×10-16<0.1，均通过一致性检验。

依据财务管理专业知识和实际应用经验，假定第一级各指标权重比为7∶3，第二级指标(信用评级与违约情况)权重比为4∶1。运用层次分析法求得二级指标权重V={0.2849，0.2849，0.1295，0.24，0.06}，三级指标权重ω={0.2849，0.0855，0.057，0.1425，0.1295，0.24，0.06}。

利用熵权法对权重进行计算：对数据进行非负化处理bij，计算第j项指标下第i个评价对象的特征比重：

计算第j项指标的熵值为：

计算第j项指标的差异系数为：

gj=1-ej,j=1,2,…,m

第j项指标的观测值差异越大，则差异系数gj就越大，第j项指标也就越重要。确定第j项指标的权重系数：

将层次分析法和熵权法求得的三级指标的权重进行简单综合，得综合权重：

Q={q1,q2,…,qn}

对每个二级指标内的三级指标的权重进行归一化处理：

将二级指标的权重与dij对应相乘，并对其进行归一化处理，综合两种方法，得出：

F1=0.2849，F2=0.26168109，F3=0.00031543，F4=0.02290348，F5=0.1295，E4=0.24，E5=0.06。

三、信贷风险实例评估

收集了99家规模相对较小且缺少抵押资产的中小微企业在2017-2019年2个年度的进项、销项发票明细、信用评级与违约情况。基于Python的AHP-熵权法，依照前述模型体系要求，进行了利息保障倍数、供求关系稳定性、息税前利润、经营利润率、利润增长率、信用评级和违约情况等7方面风险评估体系指标原始数据的整理(图1～7)。

图1 企业利息保障倍数情况

图2 企业供求关系稳定性情况 图3 企业息税前利润情况

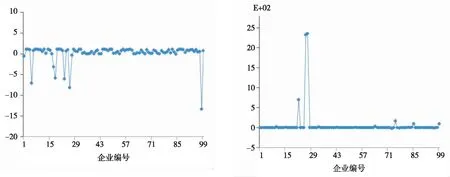
图4 企业经营利润率情况 图5 企业利润增长率情况

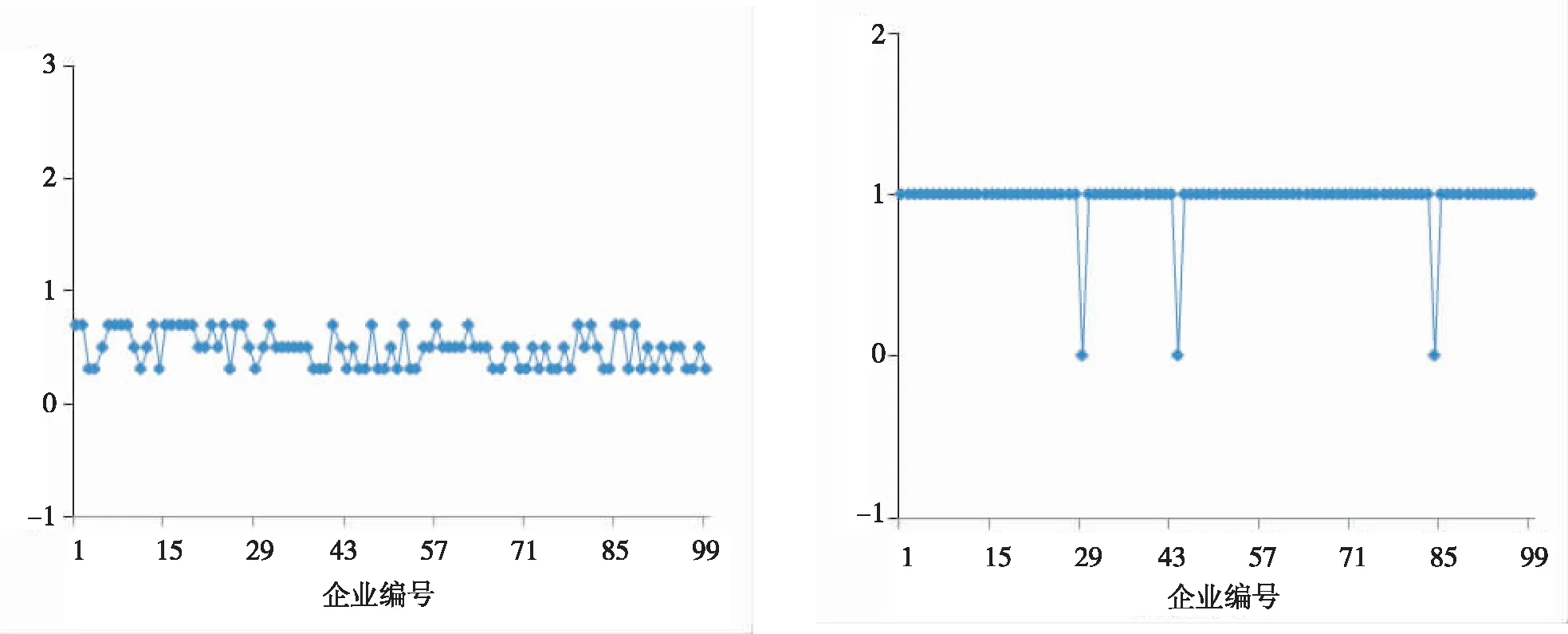
图6 企业信用评级情况 图7 企业违约情况

在此基础上，使用极差变换法对所得指标数据进行无量纲化处理。基于7方面风险评估体系指标原始数据及其赋权，99家中小微企业的信贷风险评估值见表6。

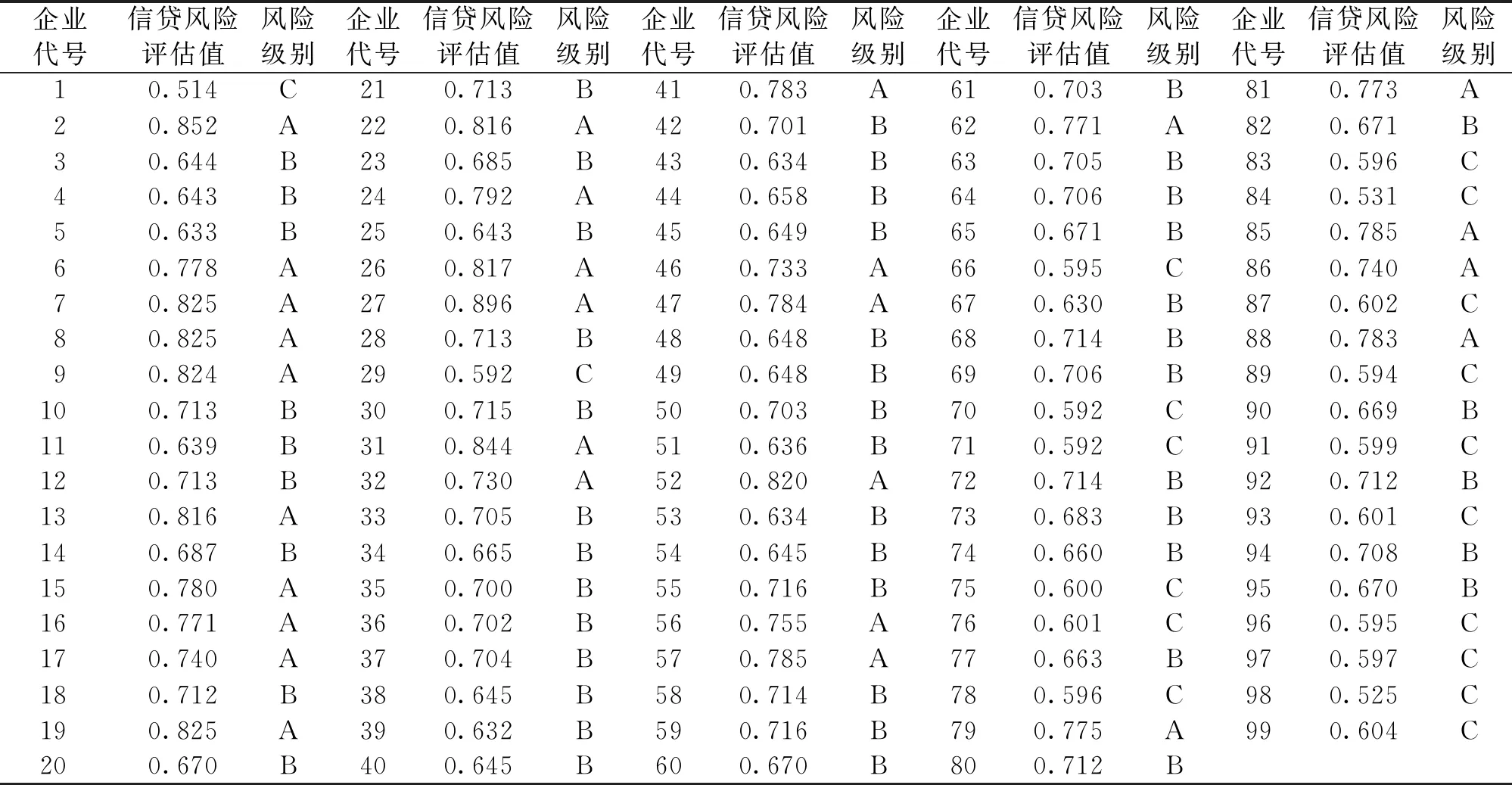
表6 99家中小微企业信贷风险评估值

中小微企业已经成为中国市场经济发展的主力军，但其往往规模相对较小，缺少抵押资产，信贷风险较大。基于Python的AHP-熵权法信贷数字分析模型较为准确地反映了该类企业的信贷风险，简化了银行评估流程，实现了数字化决策。该模型的应用对提高银行资金效率和促进优质中小微企业健康发展意义重大。