Buck变换器的降阶扩张状态观测器与无抖振滑模控制

王书旺 ,李生权 ,哀 薇 ,李 娟

(1.扬州大学 电气与能源动力工程学院,江苏 扬州 225127;2.华南理工大学 自动化科学与工程学院,广东 广州 510640)

1 Introduction

DC-DC buck converters are widely used in industrial control systems,such as electric vehicle,aerospace industry,renewable energy generation system,DC motor drives,etc.,since such converters are power electronic devices utilized to adapt the output/input voltages between the sources and load[1].It is difficult to control the converter in some situations,since a DC-DC buck converter is also a time-varying and nonlinear system due to the switching operation of the power electronics converter and the existence of some phenomenon such as chaos and bifurcation[2].Additionally,the excellent tracking performance of DC-DC buck converter is difficult to achieve due to different kinds of disturbance,variable circuit parameters and uncertain external load.The electronic parameters uncertainties exist in DC-DC buck converters inevitably,which bring great challenges to the advanced control strategies needing accurate model information[3].Thus,dynamic uncertainties are deemed as the main disturbance sources resulting in a large deviation between theoretical and actual output voltages.Different types of disturbances and modeling errors can also present severe challenges of high efficient and precision control performances for DC-DC buck converters [4].Therefore,a variety of control strategies have been explored to improve the tracking performances of DC-DC buck converter systems,such as backstepping control algorithm,adaptive control,model predictive control,intelligent control approaches,disturbance estimation based control methods,sliding mode control(SMC),and so on[5-8].These control strategies can actually improve the disturbance rejection ability of DC-DC converters in different aspects.It also can be found that the excellent robustness of the above control methods can be achieved by sacrificing the other control performances,such as the tracking performance,fast dynamical response,etc.Unfortunately,the practical applications of sliding mode control method are limited because of the disadvantages of the sensitiveness of mismatched disturbances and chattering phenomenon,since the total disturbances are conservatively reduced with large switching gains than the amplitudes of the disturbances.A type-2 fuzzy modeling method with an adaptive sliding mode controller has been proposed to attenuate the disturbances and uncertainties of the system[9].In addition,the high frequency chattering can also result in serious damage to real industrial control systems,which produces undesirable highly nonlinearity of the system dynamics.The chattering caused by sign function also involves extremely high control activity and increases electric power consumption resulting in great waste for DC-DC buck systems [10-11].Some strategies are proposed to reduce the effect of chattering in sliding mode control system.One of the most common solution to chattering problem is the boundary layer approach[12].The SMC with the boundary layer consists of a smooth function instead of the sign function.In addition,a super-twisting based on high-order sliding mode control law uses integrator to attenuate chattering[13].In[14],a SMC method based on a strict feedback nonlinear model is developed to attenuate chattering by changing the sign function into a continuous function.A novel fractional-order sliding surface based on an adaptive equivalent control law is designed to attenuate chattering and drive the system trajectories to the predefined sliding surface in finite sampling steps[15].

The traditional sliding mode control law has discontinuous term which attenuates the disturbances and leads to chattering,simultaneously.The disturbance estimation technologies are introduced to eliminate the external disturbance and uncertainty,which are the keys to solve the chattering problem.In recent years,the disturbance-observer-based-control (DOBC)method compensating the internal and external disturbances by a feedforward part has been widely applied in industrial control systems[16].The main advantage of DOBC is that it can improve the robustness of the closed-loop system without sacrificing the nominal control performance.Considering input voltage and load uncertainties in a DC-DC converter system,a nonlinear disturbance observer-based(NDOB)sliding mode control with a novel sliding surface have been developed to counteract the mismatched disturbance[17].Disturbance observer composite integral sliding mode control(ISMC)can eliminate high frequency chattering by introducing a low pass filter for the DC-DC buck system with mismatched disturbance[18].

Extended state observer(ESO)is considered as another practical disturbance estimation method and has been widely used in the real industrial control systems,which introduces a concept of total disturbance including external environmental disturbances and internal uncertainties [19].The controller based on extended state observer named active disturbance rejection control (ADRC) can estimate both system states variables and total disturbances by simple computations,then the observed value of disturbances can be furtherly employed to compensate in the feedforward channel to improve the performance of system.A linear-ADRC(LADRC) has been proposed in [20] to make the controller design and parameter tuning more practical,since the ADRC method has been used in industry control widely,such as,permanent magnet synchronous motor (PMSM) servo system,mechanical arm system,wind energy conversion system[21-26].In[27],a voltage tracking control method based on an active disturbance rejection control(ADRC)is proposed to improve the robustness of the H-bridge DC-DC converter system under matched disturbance.The ESO-based control method defines the uncertainties and changes in system dynamics including external environmental disturbances and internal uncertainties as a total disturbance,which makes the control method unique in concept and simple in engineering with superior performance.In addition,the chattering caused by SMC can also be attributed to total disturbance and compensated by ESO,while large observer bandwidth of ESO would be chosen to obtain the satisfactory disturbance rejection performance [28].In [29],a reduce-order ESO (RESO) is been designed to reduce the gains of observer to solve the problem of the weak noise reduction performance caused by the large observer bandwidth gain.Considering the pulse width modulation-based DC-DC buck converter system subject disturbances and uncertainties,a composite control method based on sliding mode control and ESO technique is developed in[30],but the large gains of observer and switching function are not mentioned.Along the research direction,an enhanced ESO method is proposed to deal with mismatched disturbances in DC-DC buck converter system,so the SMC has the ability to attenuate the disturbance without having to change the control structure of feedback part[31].Unfortunately,the chattering phenomenon caused by the relatively large switching gain is also not been considered in the reference.

A sliding mode control method based on reducedorder extended state observer (SMC-RESO) aiming at the chattering caused by the large gain of SMC and the noise amplified by the large bandwidth observer gain of ESO,is proposed to achieve the excellent voltage tracking performance the DC-DC buck converter system in this paper.The key features of the proposed strategy are as follows:1) A novel state space model based on the tracking error between the expected and the actual voltages is designed to define the matched disturbances and mismatched disturbances as a uniform matched total disturbance.Therefore,the amplitudes of total disturbance to be attenuated by the sliding mode control can be reduced by the novel mathematical model;2) The proposed sliding mode control method can significant reduce chattering without losing the robustness of the system;3) A RESO is introduced to reduce the estimated burden of ESO by a small bandwidth gain,so the high frequency noise amplified by the large gain can be solved with the proposed control method.This paper is organized as follows.The description of the nominal system mathematical model with chattering attenuation is given in Sec.2.A composite RESO-based SMC controller is proposed in the Sec.3.In addition,the stability of the proposed control method will be shown in Sec.4.In Sec.5,numerical simulation results are presented to compare the proposed RESO based SMC against the tradition ESO based SMC.Finally,Sec.5 concludes the work.

2 Mathematical model of a DC-DC buck converter

Operation mode of a PWM-based DC-DC buck converter can be shown in Fig.1.The current of the inductance and the voltage of the capacitance cannot change suddenly,so the DC-DC buck converter dynamic mathematical model with two switching modes can be deduced as follows:

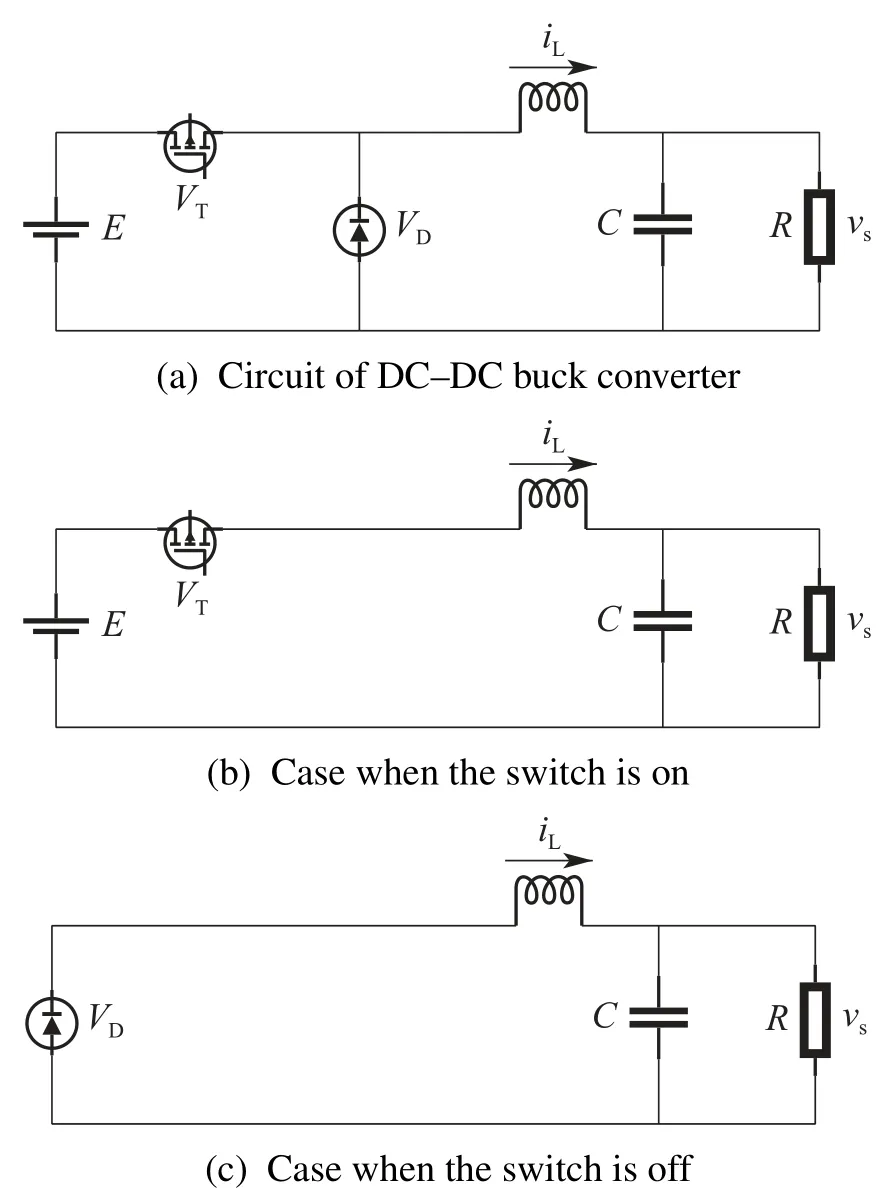
Fig.1 Average model circuit of buck converter

Case 1The switch is on

Case 2The switch is off

whereE,VTandVDare the input voltage,a MOSFET which can be turned on and off according to the input duty ratioμ ∈[0,1],and the circuit diode,respectively.The circuit parametersL,RandCrepresent circuit inductor,circuit load resistance and circuit capacitor,respectively.The currentiLand voltagevsare the current flowing through the inductor and the voltage of the load(i.e.,the output voltage),respectively.The load resistance and input voltage are usually time-varying,when the converters are applied in different operating conditions in practical situations.The nominal values of the load resistance are assumed toR0.Therefore,the average mathematical model can be described by following Eq.(3):

The system mathematical model can be rewritten as follows with definition of tracking errore1=vr-vs

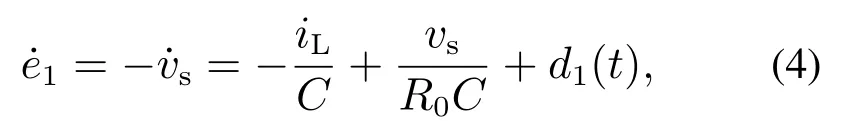
whered1(t)=represents the ratio of the change in load current to the capacitor.Due to the output voltage both ends of the capacitor,the current flowing through the load resistance cannot change suddenly,so is differentiable.The following equation can be obtained with definition ofe2=:

whered2=In addition,external disturbances and modeling error should be taken into consideration for improving the control performance.Parameterd3(t) is used to represent the uncertainties of the system,such as the modeling errors and the variation of electronic component parameters.So,the statesatisfies the following equation:

Equation(5)can be further rewritten as the following simple form with the total disturbanceDwhich can be defined asD=-d2(t)+(t)+d3(t).

The integral series standard form of buck converter should be conveniently obtained to design the controller and analyze the ESO.So,system control input can be defined as following.

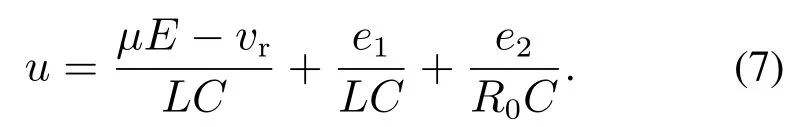
In addition,the system model can be further described as a state space model in Eq.(8) with the proposed control input in Eq.(7).

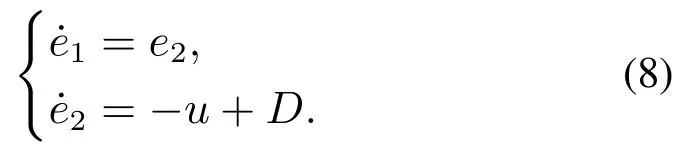
Considering the error between the actual total disturbancesDand their estimated values,system(8)can also be further deduced as Eq.(9)withv=u-and

3 SMC-RESO controller design

3.1 Reduce-order extended state observer design

The control method proposed in this paper is the sliding mode controller mainly based on Eq.(9).The robustness of the system is guaranteed by the characteristic that the sliding mode controller is insensitive to matched disturbance.The system variables that cannot be obtained directly such as ˙e1,are estimated and given by observer technology.Compared with nonlinear extended state observer(NLESO),LESO has advantage of easy parameter adjustment.Therefore,a third-order linear ESO(LESO)is commonly designed for a secondorder system(9)as follows:

wheree0is defined as the tracking error of the observer.The bandwidth of LESO(10)is expressed by.The estimated values ofe1andcan be defined asz1andz2,respectively.The extended state variablez3of LESO is the estimation of the total disturbanceD,i.e.,ˆD.In addition,a second-order RESO is proposed to reduce the bandwidth of the observer due to the system statee1which can be measured directly.Based on the system Eq.(9),the RESO is designed as follows:

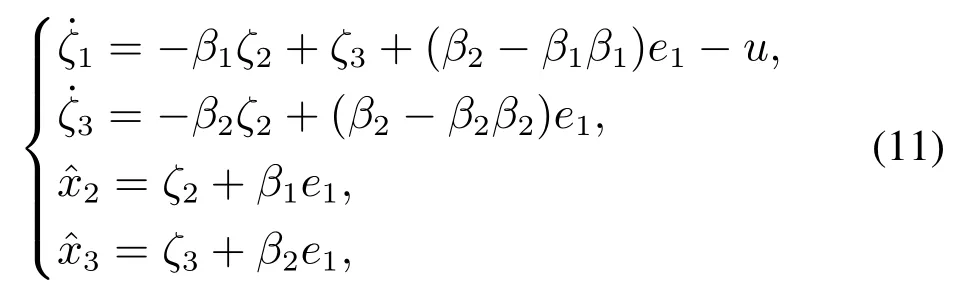
whereβ1,β2are defined as the gains of the RESO,ζ2,ζ3denote the states of the RESO.The outputs of RESO are,which represent the estimate value ofandD,respectively.Bandwidth method has been applied in the parameters tuning,soβ1=2ω0,β2=.The bandwidth of the RESO (11) is expressed byω0.The speed of RESO tracking system disturbances and dynamic uncertainties can be improved by abandoning the estimation of system first order state.

3.2 Sliding mode control design

The novel modeling method proposed in this paper has two advantages.Firstly,the mismatched disturbance can be transformed into matched disturbance,since it is unnecessary to consider the types of total disturbances in the design of SMC controller for DC-DC buck converter system.Additionally,the disturbance,i.e.,observer error between the actual total disturbances and their estimated values,should be attenuated by SMC in Eq.(9),which is smaller than that in Eq.(8).Therefore,the sliding mode surface is defined as follows:

whereλis a designed constant of sliding mode surface.Exponent reaching law Eq.(13) is selected to improve the rapidity of sliding mode control and reduce chattering,simultaneously:

whereηis the parameter of sign function to be designed.The control coefficientkrepresents the rate that system reaches at the sliding mode surface.The disturbance rejection ability and the approaching rate can satisfy practical requirements by choosing appropriate values ofηandk.So the derivative of sliding mode function is deduced as follows:

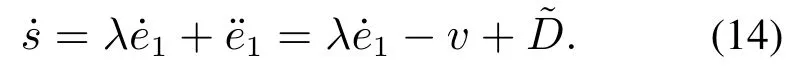
According to Eqs.(13) and (14),the sliding mode control law can be obtained as following Eq.(15).

The design of switching gainη′in the control law satisfiesη′≥||+|η|.The magnitude of chattering depends on the value of.The chattering free can be achieved when disturbance is approximately to zero with accurate estimated total disturbance by RESO.Therefore,the SMC-RESO control law is deduced as follows by achieving ˙e1,information from RESO:

Appropriate parameters can be selected to satisfy the different requirements.The disturbance rejection ability of the closed-loop system can be improved by increasing the bandwidth of RESO.The switching gainηin exponent reaching law can select 0 when the total disturbance is estimated accurately by RESO.Meanwhile,parametersλandkare used to improve the rapidity of the system.According to Eq.(7),the duty ratio can be deduced from Eq.(16):

The SMC-RESO control system for DC-DC buck system is shown in Fig.2.It can be found in Fig.2 that only the output voltagevsneeds to be measured.Therefore,the proposed SMC-RESO control method is beneficial to the application of practical engineering,because the inductance current is not a value that must be measured in the controller design for DC-DC buck converter system.The modeling errors caused by electronic components in Eq.(17) will be summarized asd3(t).Meanwhile,the ESO will regard it as the total disturbance.The results of modeling errors added to the system will be shown in the simulation.

Fig.2 Control system structure based on the proposed control method for DC-DC buck converter

Lemma 1[32]Considering a non-linear system=F(x,w) with the condition of input-to-state stable (ISS),if the inputs satisfy→0,then the states satisfy

4 Stability analysis

4.1 Convergence analysis RESO

whereρ=-ω0＜0,as long asβ2e1-is bounded.The poles of the system will stay in the left-half complex plane,that is to sayε2,ε3will gradually converge to zero.Therefore,it can be proved that the designed observer is globally convergent.

4.2 Proof of sliding mode controller stability

The closed-loop control system of DC-DC buck circuit consists of Eqs.(9)-(16).The stability of the sliding mode controller can be proved by using Lyapunov stability criterion with following Lyapunov function:

The following Eq.(22) can be obtained by taking derivative of along dynamics Eq.(14).

By substituting Eq.(15)into Eq.(22),Eq.(22)can be further rewritten as Eq.(23):

According to Assumption 1,the total disturbances including mismatched and matched uncertainties and disturbances are bounded,so the state variableε3in Eq.(29)is also a bounded variable.

whereη′is the designed switching gain of sign function which satisfiesη′≥|η|+||＞|η|+|ε3|≥0(η≥0).The designed composite controller satisfies Lyapunov stability criterion according to Eq.(24).Therefore,the system can reach the sliding mode surface from any initial condition in finite time with an appropriateη′.The sliding motion is described as Eq.(25)when system state variables move on the sliding mode surfaces=0:

Equation (26) can be obtained by substituting into Eq.(25):

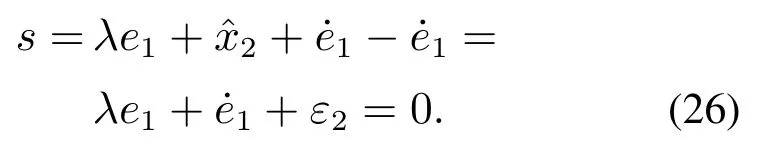
The following Eq.(27) can be further deduced along Eq.(26):

5 Simulation and analysis

The simulation verification is based on MATLAB/SIMULINK with the proposed average mathematical model in this paper.The desired output voltage value is set to be 5 V and the DC-DC buck converter circuit parameters is shown in Table 1.To compare the disturbance rejection ability of SMC-RESO and SMC-ESO methods,the external disturbances and internal uncertainties in actual DC-DC converter have been studied in this section.First,the load resistance changing from 100 Ω to 130 Ω and 75 Ω at 2 s and 4 s is regarded as the external disturbance in Fig.3.A pulse signal with 1 V value is added to the input voltage at 2 s to take the modeling errors into consideration.The impulse disturbances are also added to the inductance and capacitance which changes from 4.7 mH to 2.2 mH at 4 s and changes from 1000 μF to 400 μF at 6 s,respectively.The response curve of modeling errors is shown in Fig.4.In addition,it is inevitable that the measurement noise caused by sensors exists in practical industry,therefore,random noise is added into the output voltage.The comparison results of noise rejection ability between SMC-ESO and SMC-RESO are shown in Fig.5.Finally,the chattering attenuation ability with the proposed modeling method is shown in Fig.6 by choosing different switching gains.

Table 1 Parameters of the DC-DC buck converter

Similar rapidity is chosen for two methods to show the advantages of the sliding mode method proposed in this paper.The parameters in SMC-ESO controller are chosen asλ=50,k=0,η=0,ω=100,while the parameters in SMC-RESO controller are selected asλ=80,k=0,η=0,ω=80.The output voltage response curves under the load disturbance and modeling error are shown in Fig.3.It is observed that the modeling error can be attenuated effectively by the two ESO based control method.In addition,the SMCRESO controller produce a better convergence rate than that of the SMC-ESO controller when the two control methods achieve the similar rapidity.This is because the first-order statee1can be measured directly,so the total disturbance can be estimated more quickly.Although the bandwidth of ESO is the same as that of RESO,but the observer gain of ESO is much larger than that of RESO.Therefore,the impact of the high frequency noise on the DC-DC buck system can be reduced by RESO.

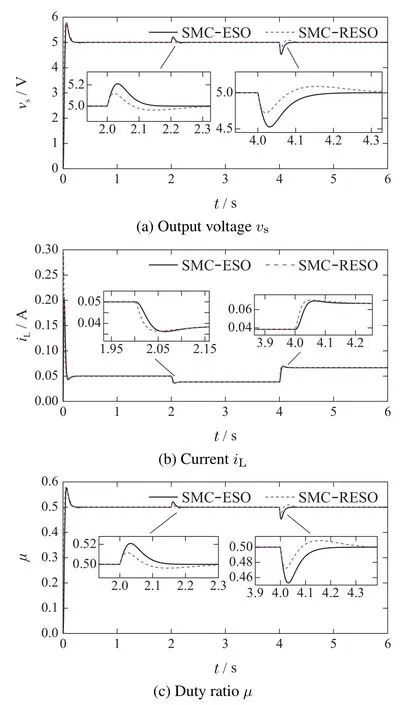
Fig.3 Response curves under SMC-RESO controller and SMC-ESO controller when the load resistance is changed

It is impossible to keep the electronic parameters of the DC-DC buck system invariant,so the modeling errors should be taken into consideration.Fig.4 shows the response curve of the SMC-ESO controller and SMCRESO controller under the modeling errors.It is clear that the SMC-RESO controller has strong disturbance rejection ability when the input voltage changes.It also can be found that the SMC-RESO controller can keep invariable when the inductance and capacitance change greatly,while the SMC-ESO controller is difficult to attenuate these disturbances.It is necessary to take the high frequency noise into consideration,because the measurement noise unavoidably exists in the actual industry control systems.Appropriate parameters are chosen to make SMC-ESO and SMC-RESO have similar rapidity.To have a fair comparison,the bandwidth of ESO and RESO are selected as 80.The response curves of output voltages are shown in Fig.5.It can be found in Fig.5 that the sensitivity of noise has been significantly improved by RESO method because the observer gain of RESO is litter than tradition ESO method.In Fig.6,to verify the chattering attenuation ability of the modeling method proposed in this paper,three switching gainsη=0,5,10 are chosen to compare the duty ratioμchattering amplitude,respectively.It can be observed that the disturbance rejection ability is similar in three cases,but chattering is close to zero whenη=0.Compared to the casesη=5,10,the voltage tracking curve has chattering free feature whenη=0.The larger switching gain is,the greater the chattering amplitude and the worse the tracking performance.This advantage directly guarantees the chattering attenuation ability of the SMC-RESO method.The tracking error state space model proposed in this paper is also another significant factor to attenuate the chattering in SMC.The response curve of output voltage under the tradition SMC controller and SMC-ESO controller is shown in Fig.7.The traditional SMC controller parameters areλ=20,η=50,while the SMC-ESO controller parameters areλ=10,η=0,ω=70.It can be found that the SMC-ESO controller under the proposed modeling method achieve a better chattering attenuation result without loss robustness.

Fig.4 Response curves under SMC-RESO controller and SMC-ESO controller with modeling errors

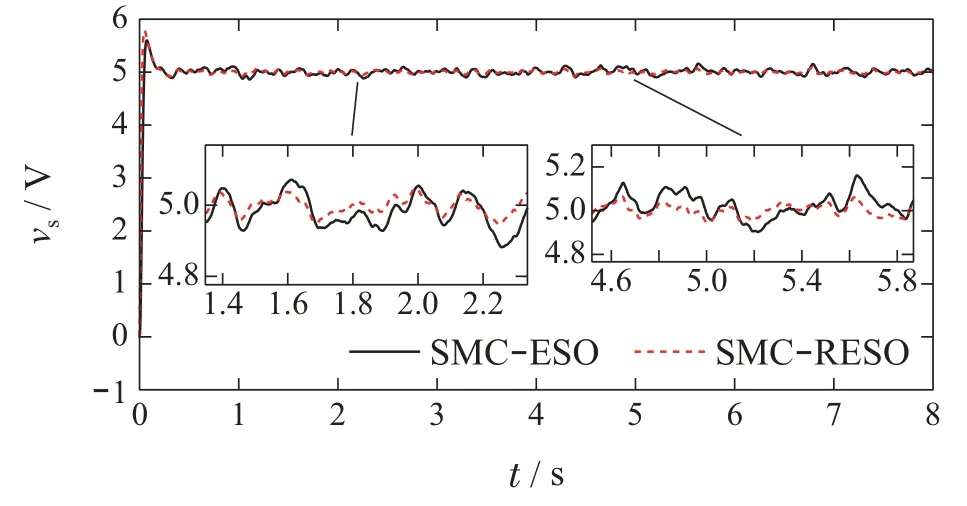
Fig.5 Response curves under SMC-RESO controller and SMC-ESO controllers with measurement noise

Fig.6 Control curve of duty ratio μ under different switching gains

Fig.7 Response curves under SMC-ESO controller and tradition SMC controller

It can be seen from the comparative verifications that the chattering of the traditional SMC controller can be reduced effectively under the proposed tracking error state space model.In addition,the proposed SMCRESO control method also has better disturbance and high frequency noise rejection performance than SMCESO method.

6 Conclusions

A SMC-RESO controller based on a novel tracking error state space model is proposed to improve the voltage tracking performance of a DC-DC buck with system uncertainties.The superiority of the proposed control method is systematically analyzed,then the tracking performances of SMC-RESO method and SMCESO method are compared by simulation results for a DC-DC buck converter subject total disturbances in this paper.In addition,the simulation results of several cases show that the proposed SMC-RESO controller with the novel modeling method can attenuate the chattering and also possess the robustness.In the future,the experiments can be carried out after the establishment of the experimental platform.