基于遗传算法的移动机器人路径规划及人机协同控制研究

杨国庆，方振江，吴 昊

（天津城建大学控制与机械工程学院，天津300384）

针对目前移动机器人在作业时，对环境的适应和理解能力仍有不足，提出采取人机协同控制来适应环境，提高移动机器人作业效率的方案.在进行人机协同控制之前，机器人的路径规划问题是第一个要解决的问题.路径规划是为了让机器人在一定的约束条件下（距离最短，耗时最小等），从起始地点向终点移动，最终找到一条可行路径[1].

目前，按照对周围环境信息是否已知，将路径规划问题分成全局、局部规划两类.当环境已知时，可采用可视图法、自由空间法、栅格法等.反之，就需借助传感器获取环境信息，并对机器人进行局部路径规划.常用的局部规划方法有人工势场法[2]、速度分解法、神经网络算法等.但是它们都由于自身的局限性和独特性而无法通用.遗传算法依靠其自身较强的全局搜索能力、强适应力、灵活性、鲁棒性等在路径规划方面有一定的成果，但也存在容易得到“最优解”和易陷入局部最优的缺点.文献[3]改进了传统遗传算法中的交叉和变异算子，增强了全局和局部搜索能力，提高了算法计算效率，但在复杂环境下效果一般.文献[4]通过生成可行路径辅助点的方法加速遗传算法收敛，但是其采用二维实数编码，这样做使得编码方式与一维实数编码相比更复杂，随着种群的增加，增加了系统的存储量，使后续计算更复杂[5]，使寻优速度下降.

本文将采用先全局再局部的规划方法，采用传感器感知环境信息，并对遗传算法[6]进行以下改进：优化初始种群，使其开始就获得比较好的父代，根据要求建立适应度函数，优化选择、交叉、变异算子，通过灾变防止遗传算法过早得到“最优解”.最后结合实际发现其在狭窄、路况不佳的路段，机器人无法自主找到真正的最优解，于是提出人机协同控制，对其进行进一步优化.

1 基于改进遗传算法的机器人路径规划

遗传算法的并行性，以及操作时的灵活性、适用性使其成为了一种被广泛采用的算法[7].在进行路径规划时，将传统的遗传算法进行改进后，设计的流程图如图1所示.

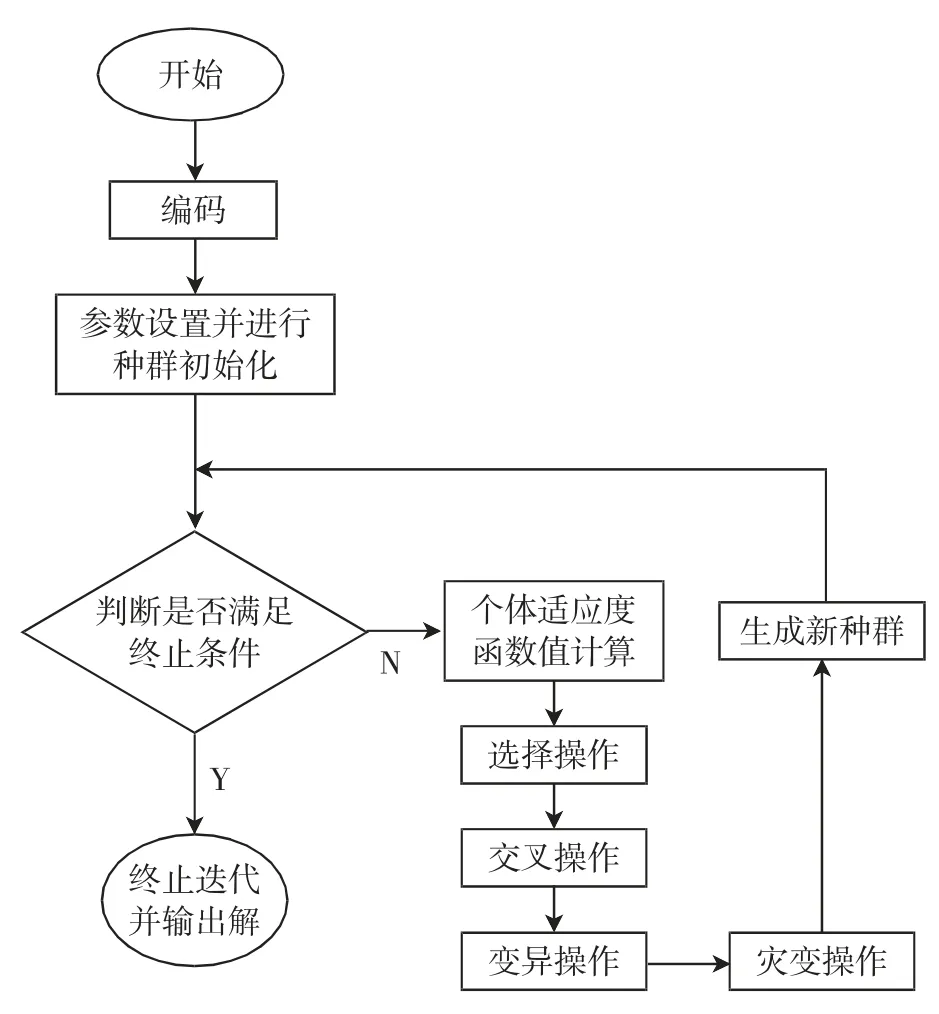
图1 改进遗传算法的流程图

第一步，确定种群中每个个体的编码方式，并初始化种群；第二步，判断是否满足终止条件，若满足终止条件则退出，并得到最优解；第三步，若不满足终止条件，则由适应度函数计算种群中各个个体的适应度；第四步，进行基本遗传操作（选择、交叉、变异）；第五步，进行有限次数的灾变；第六步，生成新种群并转到第二步，依次循环.

1.1 环境建模和编码处理

用栅格法[8]对移动机器人的移动空间进行二维环境建模[9]，其周围环境信息（障碍数量、方位等）已知.为了方便建模，将其看成可以随机移动的质点.建立环境模型时，忽略机器人可以越过的障碍.白色部分为可以到达的区域，红色部分为障碍物区域，记原点处栅格序号为1，每层按照从左到右递增1的规律，依次标出各格栅的序号，相邻的上、下层栅格中上层的栅格序号比下层的大15.设起点为S，终点为G，机器人的工作环境模拟图如图2所示.

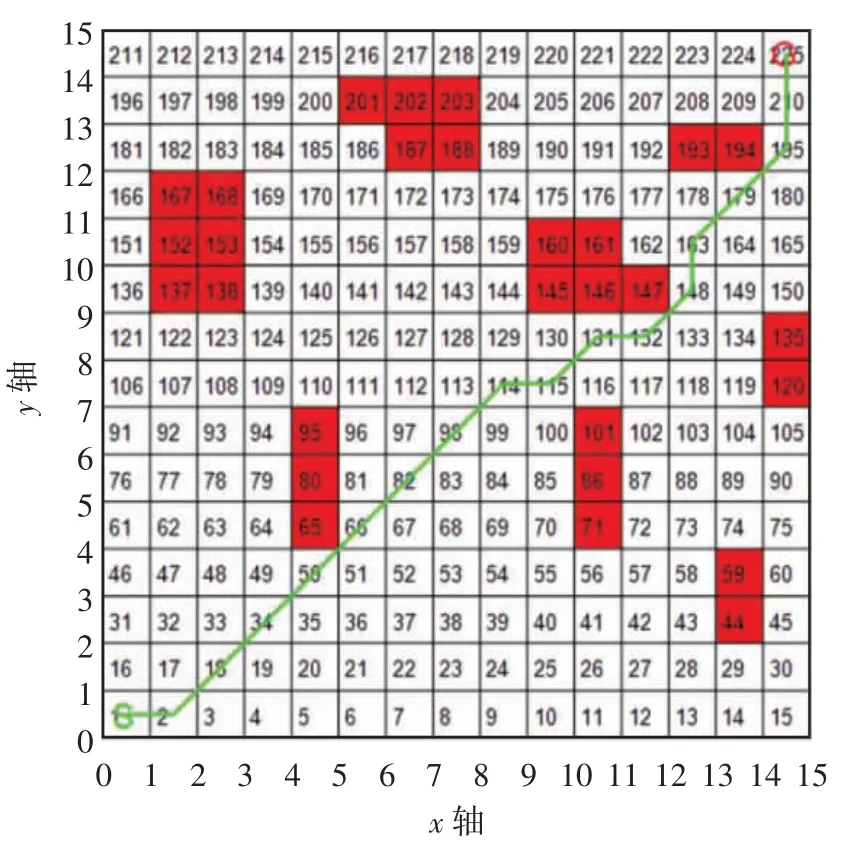
图2 机器人的工作环境模拟图

编码时采取一维实数编码，该编码方式跟二维编码方式相比在存储时减少了内存的消耗，计算时也更简单[10].记起始栅格序号为S，目标栅格序号为G，然后由N个点组成一条，则其中一条染色体如图3所示.

图3 路径编码图

1.2 初始化种群优化

随机初始化种群，虽然使得种群可以多样性，但会造成父代种群质量偏低，减慢了求最优解的速度.因此对该操作做出改进，即先产生一条可行路径.记0区域为移动机器人当前所在的位置，其周围栅格如图4所示.

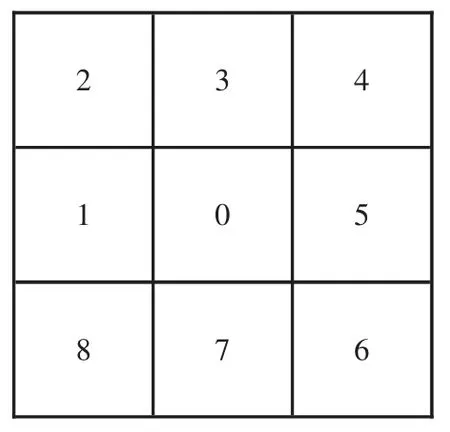
图4 周围栅格

具体方法如下：

第一步，选取机器人周围{1，8，6，7}这4个栅格作为下一步所要到达的栅格，记下一步要到达的点到终点的距离为i，该点被选中的概率为pm.考虑到当前栅格位置可能处于最外圈，{1，8，6，7}当中会有一些栅格不存在，因此分成两种情况.若下一步所要到达的点无法到达，记i=+∞，则pm=0.若下一步的点可以到达，则表示为

第二步，随机生成一个两位数n（n≠0），然后k=.选一个最接近概率值pm的栅格作为下一步的目标栅格.

第三步，若下一个栅格是可行栅格则跳到第一步继续寻找下一个栅格.若当前找到的栅格为不可行栅格则淘汰当前栅格并不再使用，并转到第二步.若备选的栅格都是障碍栅格，则全部淘汰并选择新的方向栅格{2，3，4，5}，并转到第一步计算被选中的概率pm.

第四步，判断是否到达目标点，若到达，则保存当前路径，并生成下一个个体直到到达种群规模.

1.3 适应度函数的建立

建立合适的适应度函数对提升遗传算法的稳定性有很大的帮助，不够好的适应度函数会使算法无法快速地找到最优解甚至陷入局部最优.适应度值大小反映了路径的优良程度且与其成正比[11].为了更快地到达目标点，改进后的适应度函数为

l为起始点到目标点的路径长度，其具体公式为

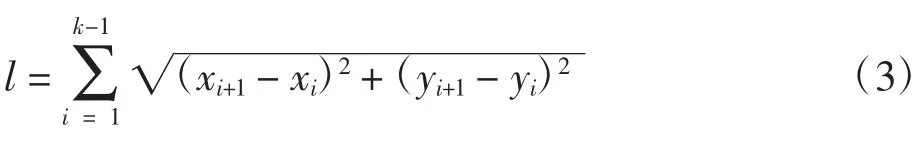
式中：xi表示第i个点的横坐标；xi+1表示第i+1个点的横坐标；yi表示第i个点的纵坐标；yi+1表示第i+1个点的纵坐标.

1.4 遗传算子的设计

1.4.1 选择算子的设计

选择操作是为了保证种群内优秀的基因得以留存.轮盘赌法使得个体适应度大的容易被选择，但是由于其随机性可能导致种群中适应度差的个体易被选择.因次，若单一的采用轮盘赌法并不可靠，因此提出了一种改进方案，在首次选择时先进行锦标赛选择法，取2个个体进行比较，并保留具有最高适应度的个体.在下次选择时采用轮盘赌法进行选择，并与上一次留下的个体进行适应度比较，大的保留并进行下一轮选择，在后面选择时，都须采取此种策略[12].

1.4.2 交叉算子的设计

交叉算子的设计是为了提升子代基因的优良程度，即在繁殖时，保留较好的基因.目前交叉方式有多点交叉、单点交叉[13]、部分映射交叉等.采用除起点外第一个相同的点进行单点交叉，是为了尽可能保证路径的连续性和可行性.在交叉时随机两两交叉然后父子代个体按照适应度值排序，设置一定的淘汰率如10%，使种群更好地朝着最优方向发展.

1.4.3 变异算子的设计

由于变异具有不确定性，可能使得原本可以通过的线路在变异后无法通过，结果如图5所示.

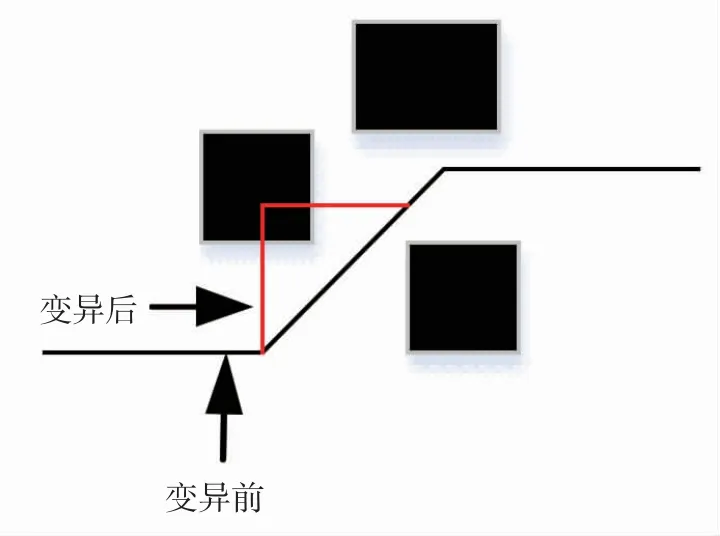
图5 不确定变异图

为了保障路径的可行性，采用一种改进的变异策略.随机选择可行路径上的某一栅格（除起点、终点外），将其视为障碍栅格并删除，然后原路径就会一分为二，含有起点的路径称为前向路径，含有终点的路径称为后向路径，最后重新寻找一条连接路径将之前得到的两条独立路径连接，就能得到一条完整的可行路径.连接路径的起点就是前向路径的终点，连接路径的终点就是后向路径的起点.连接路径的寻找策略：采用本文1.2初始化种群优化的策略来得到一条连接路径.

1.4.4 自适应交叉、变异策略

自适应遗传算法[14]使得种群进化时对交叉、变异率的选取更加科学.因为在进化前期，一定的交叉、变异率将会让种群朝着更好的方向发展，但是在种群进化后期，固定的交叉、变异率就会显得过高，从而使得本已优秀的个体进行不稳定的进化，反而使得种群退化.

传统的余弦自适应交叉、变异函数如下

式（4）-（5）中：Pc、Pm为选取的交叉率、变异率；Pcmax、Pcmin为交叉率的最大值、最小值；Pmmax、Pmmin为变异率的最大值、最小值；fmin、fmax是种群当中最差、最优个体的适应度值；favg为种群的平均适应度值；f为当前个体的适应度值；f′为两个个体进行交叉操作时，适应度值较大者的适应度值.

logistic函数如下

logistic函数在起始阶段和末尾阶段有着很好的平滑度，这两个阶段的函数值的减小速度十分缓慢，logistic函数值都在0到1的范围内，跟交叉率与变异率的取值范围一致.因此可以引入该函数来优化余弦自适应遗传策略.

在种群实际进化时，随着迭代的进行，交叉率、变异率不断变化，种群在不断进化.因此，在自适应公式中加入迭代次数这个因素很有必要.改进后的自适应交叉、变异函数如下

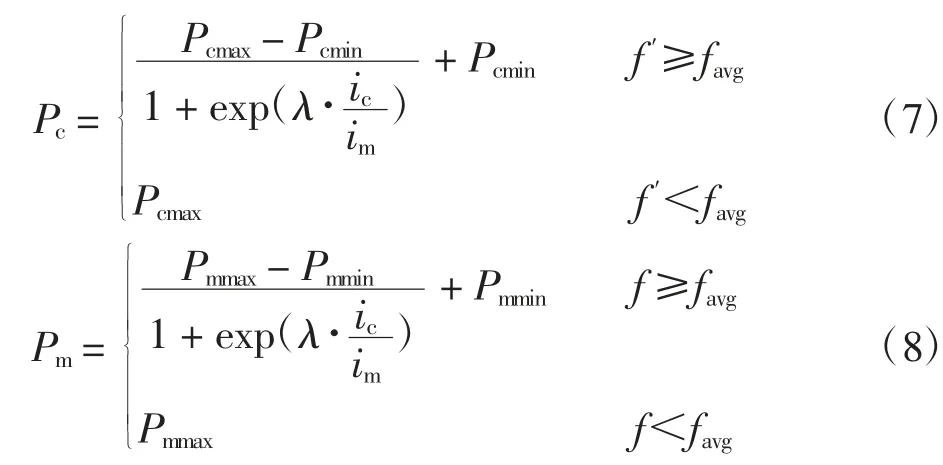
式中：ic为当前迭代次数，且从1开始；im为迭代次数上限；λ为衰减系数.

该公式说明在进化后期，种群个体不断趋于最优时，随着迭代次数的增加，变异率在不断地衰减.

上述提到的两种自适应遗传策略进行对比时，二者的交叉率与变异率曲线变化趋势一致，因此只要比较该自适应函数与余弦自适应函数的变异率变化曲线的优缺点就能类推二者交叉率变化曲线的优缺点.变异率变化曲线如图6所示.

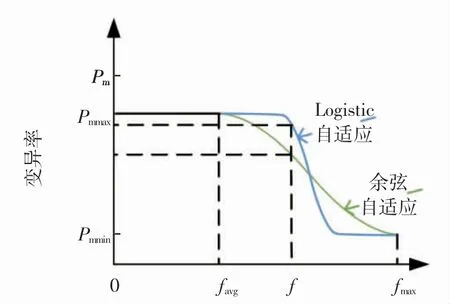
图6 logistic自适应和余弦自适应变异率变化曲线

通过分析图6，发现改进的自适应遗传策略在种群进化前期，即适应度值在区间[favg，（favg+fmax）/2]的个体变异率高于余弦自适应遗传策略的变异率，在种群进化前期保持较高的变异率，有利于种群的进化；在种群进化的稳定阶段，即适应度值在区间[（favg+fmax）/2，fmax]改进的自适应遗传策略的个体变异率要小于余弦自适应遗传策略的变异率，在种群进化后期，较低的变异率有利于保护种群当中的优良个体.另外，其变异率的减小速度与余弦自适应遗传策略相比也更平稳.这样分布的变异率说明本算法更加科学.

1.4.5 灾变算子

灾变[15]就是杀死种群内最优的个体，使得种群远离局部最优，避免了种群过早得到“最优解”，同时也使得种群更加多样化.但是如果种群一直在经历无限次的灾变，那么种群将无法得到最优个体，种群的结构也会被破坏，种群会无法进化，这样做显然是不可取的.因此本文设置了最大的灾变次数如下

设计的灾变公式如下

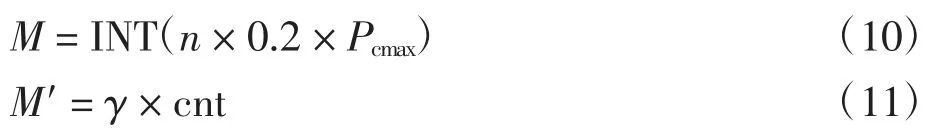
式中：INT表示取整操作；n表示种群大小；M表示种群进行灾变时设置的计数器的初始计数值，当发生灾变时，M值就会减1.如果M值在没有变成0之前就产生了新的最优个体，取当前M值记为cnt，并引入权重系数γ，γ取1.5.重新设置新的计数值为M′，不断重复灾变过程直到达到灾变次数的最大值.

1.5 未协同时的路径规划模拟仿真

设3种算法的最大迭代次数im为180，种群大小n为200.第一种算法为一般遗传策略，交叉率为0.4，变异率为0.04，后两种算法分别为余弦自适应遗传策略以及改进的自适应遗传策略，Pcmax为0.4，Pcmin为0.3，Pmmax为0.08，Pmmin为0.04.一般遗传策略、余弦自适应遗传策略、改进的自适应遗传策略路径模拟图和各自的迭代次数与路径长度关系图如图7-12所示.

分析图7、9、11发现一般遗传策略的路径存在明显的缺陷（栅格113、128），由图8、10、12可知，一般遗传策略在第75次迭代才找到最短路径，比余弦自适应策略多了约42次，比改进的自适应策略多了约60次，且改进的自适应遗传策略最优路径起始距离最短.为了确保实验的可靠性分别对每种算法进行15次测试，统计后的数据如表1所示.

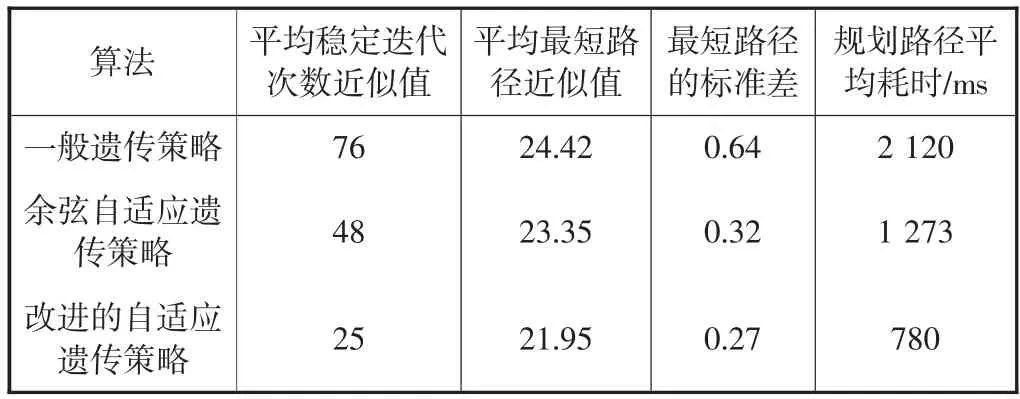
表1 各算法测试结果

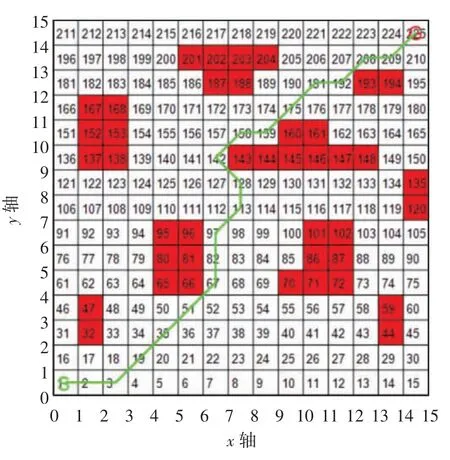
图7 一般遗传策略路径模拟仿真图

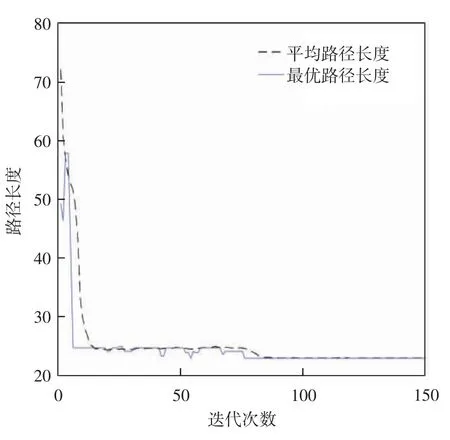
图8 一般遗传算法迭代次数与路径长度关系图

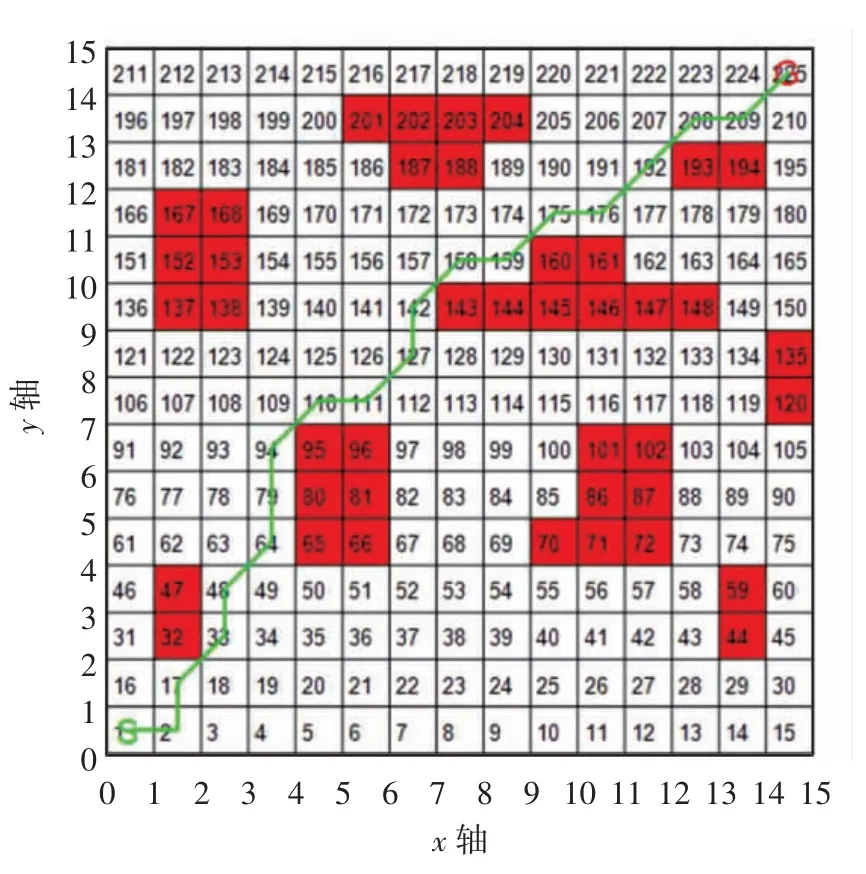
图9 余弦自适应遗传策略路径模拟仿真图

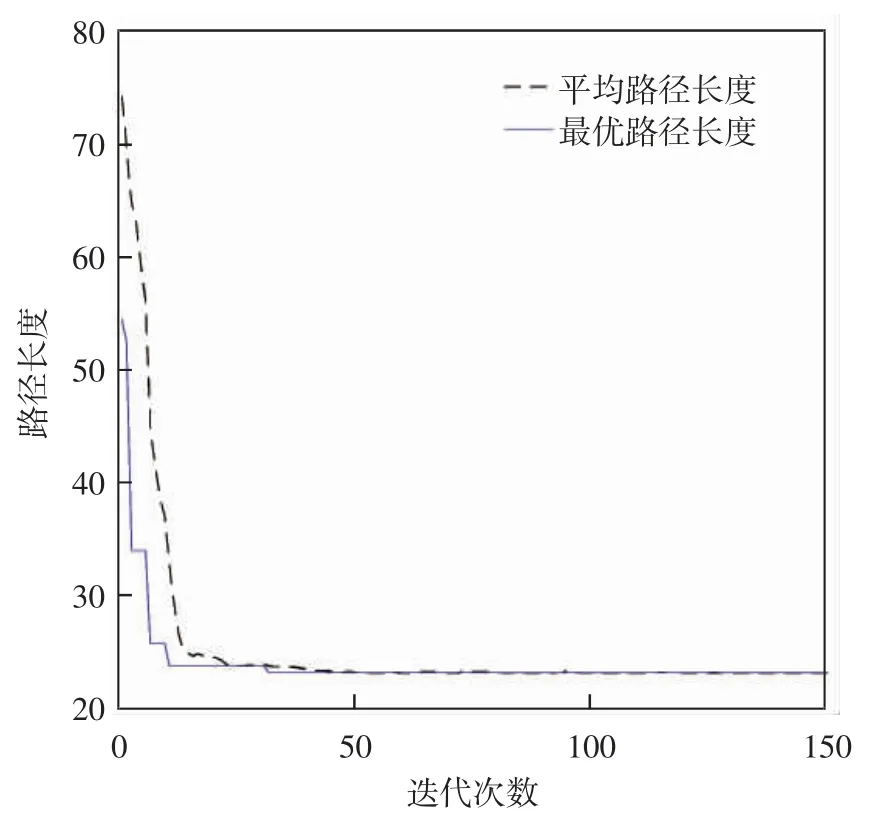
图10 余弦自适应遗传算法迭代次数与路径长度关系图

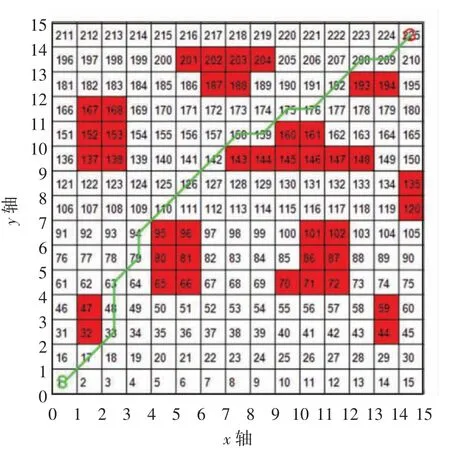
图11 改进的自适应遗传策略路径模拟仿真图

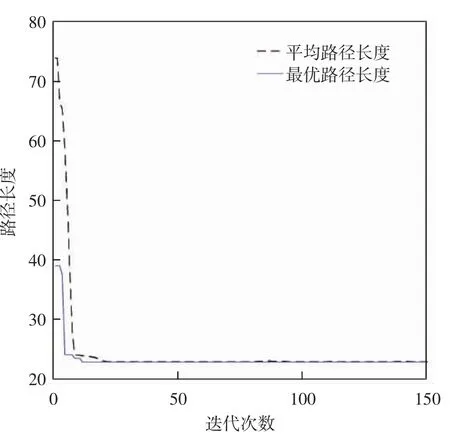
图12 改进的自适应遗传算法迭代次数与路径长度关系图

通过对表1数据的分析，发现改进的自适应遗传算法在平均稳定迭代次数近似值、平均最短路径近似值等方面都比一般遗传算法要好而且跟第二种算法相比其能更快地稳定，所找到的最短路径变化相对稳定，所需时间也短于其他两种算法.

2 协同控制处理

人机协同[16]的关键在于由人和机器一起控制，采用远、近端控制机器人的方法代替机器人自主规划路径.人机控制界面用Python和Eric6设计完成，主要采取4种工作模式.

第一种为主从模式，全程由远端操作人员根据传回的现场图像进行远程遥控.

第二种为全自动模式（未进行协同控制），操作人员先在远端设定好起始位置和终止位置，通过计算机生成最优路径，然后把规划好的路径传送给移动机器人，移动机器人再通过自身解析变成各种运行命令，最后移动机器人按照规划好的路线运行.

第三种为监控半自动模式（采用人机协同控制），监控半自动模式跟全自动模式类似，是在全自动模式运行的基础上加上监控.当远端操作人员觉得当前路径不可行时，可以按照人机交互界面上的控制按钮进行控制，重新规划路径.

第四种为关键点监控模式，当环境数据采集机器人要进行作业时，一定会对移动机器人运行环境内多处位置进行数据采集，那么这些点就是路径关键点.远端操作人员拟合这些路径关键点并设计出一条可行路径.

第五种为语音控制模式，在以上控制模式的基础上加入了语音控制，近端人员根据现场环境控制移动机器人运动.为了防止在控制移动机器人运行时出现顺序错乱的问题，设置语音模式优于其他控制模式.

实验场景如图13所示.

图13 实验场景图

2.1 实验内容及过程

（1）设置移动机器人的起始点S和目标点G，获取移动机器人当前的环境信息（障碍物的位置、障碍物的数量等），用膨胀法对障碍物进行处理，即将小于一格栅格的障碍栅格变为一整格栅格，记障碍栅格为红色，自由栅格为白色，采用15×15大小的栅格来表示移动机器人的运行环境.在环境建模时，假设栅格195、栅格210为环境复杂的路段（路况差、存在不停移动的障碍、有人拦路等情况，在初始环境模拟图上未进行特殊标注），在未经过人为判断时，机器人认为其能通过，实际上无法通过，其初始环境模拟图如图14所示.

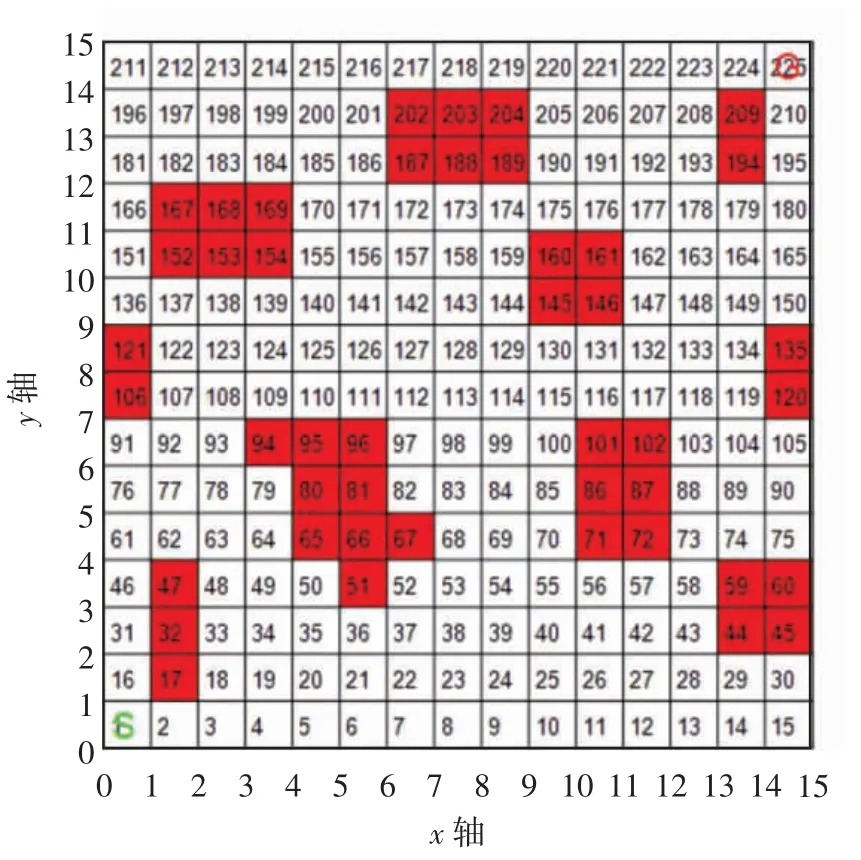
图14 初始环境模拟图

（2）采用全自动模式（未进行人机协同控制）以及监控半自动模式（人机协同控制模式）分别进行10次实验并对周围环境数据采集.

（3）对人机协同实验的结果进行分析.

2.2 实验结果分析

采用全自动模式时，某一次实验过程中的上位机界面如图15所示.

图15 全自动模式下的上位机界面图

采用监控半自动模式时，某一次实验过程中的上位机界面如图16所示.

图16 监控半自动模式下的上位机界面图

采用上述两种模式进行10次实验后得到的数据结果如表2所示.

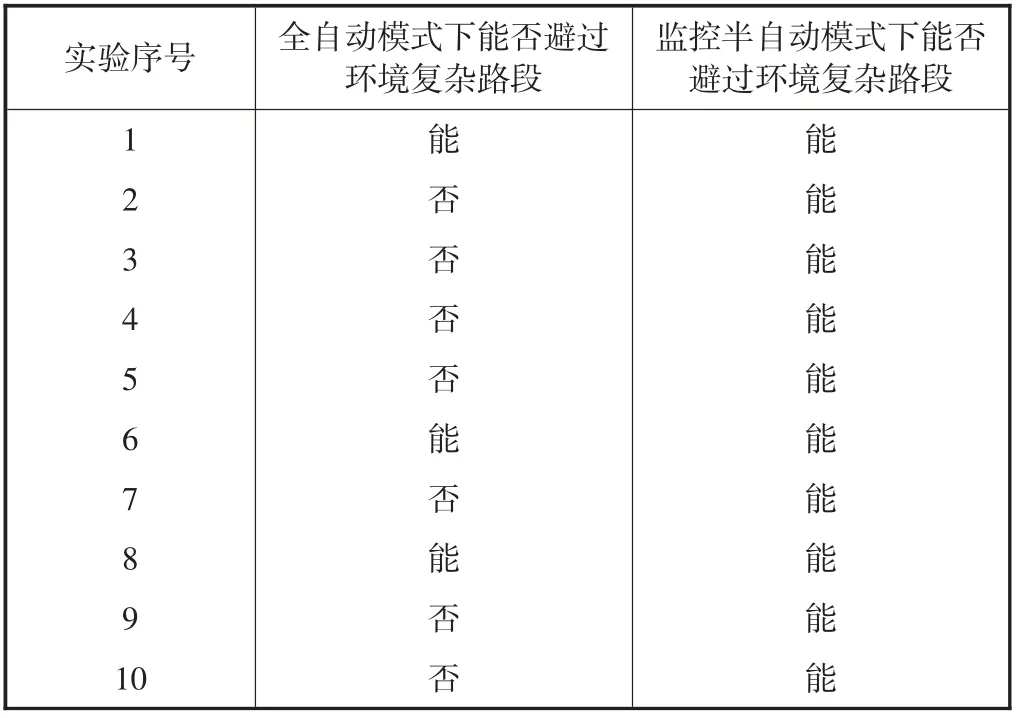
表2 10次实验数据结果

采取上述两种控制模式下的运动轨迹对比图如图17所示.

通过观察分析表2中的数据，可以发现：当采取监控半自动模式时，移动机器人均避过了环境复杂路段，而在全自动模式下的10次实验里只有3次避过了环境复杂路段.通过分析图17，发现全自动模式下移动机器人规划的路径将栅格195、210视为无障碍路段，与实际不符，且经过了环境复杂路段195、210，实际上应避过这些路段.而监控半自动模式下，移动机器人通过人的决策，会将上述两个栅格当作障碍栅格，从而避过了障碍物，安全到达了目标点.通过上述分析可以证明当移动机器人采取人机协同控制时，机器人可更好地在复杂的环境当中进行作业.

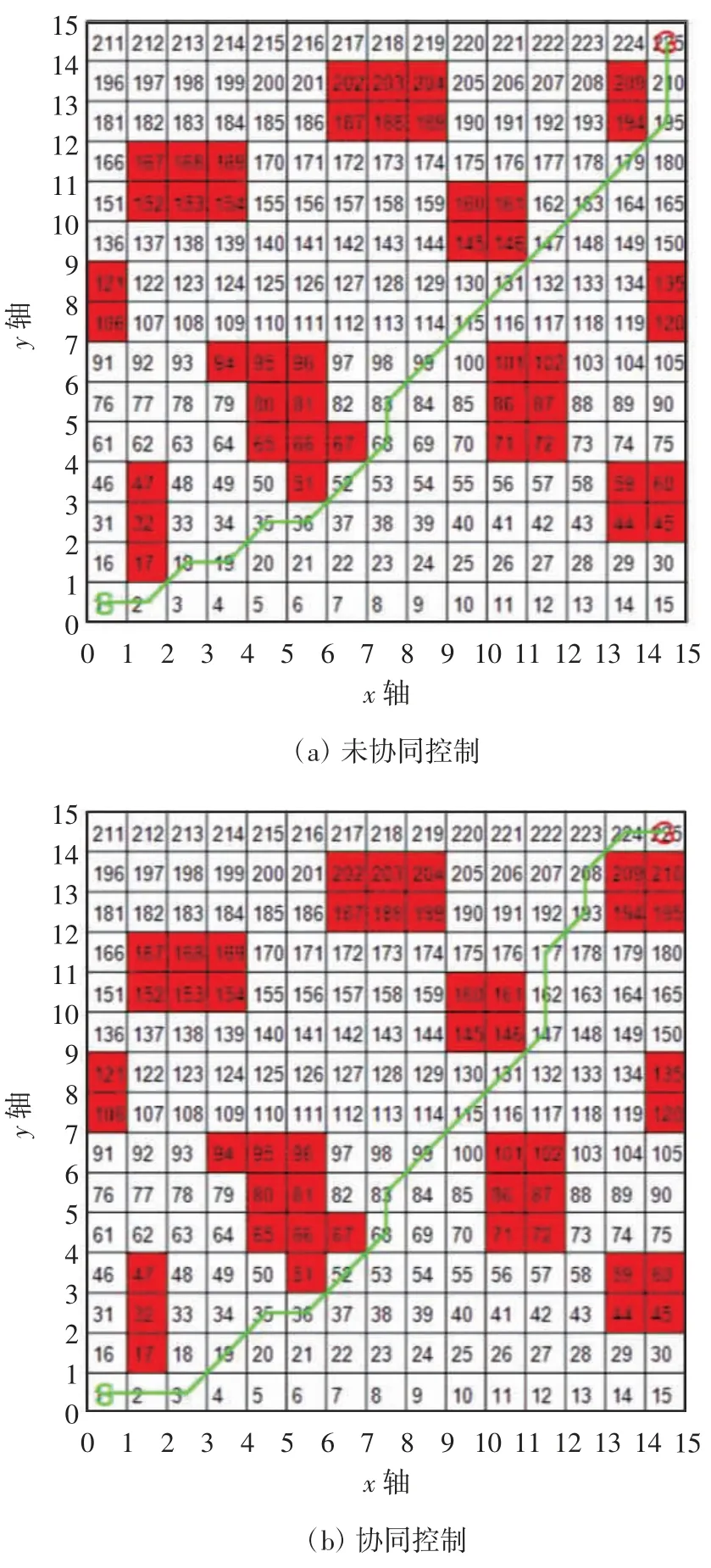
图17 未协同和协同控制路径轨迹对比图

3 结语

在进行人机协同控制之前，需先进行路径规划.在路径规划时，为了解决遗传算法过早得到“最优解”、易陷入局部最优、收敛速度慢的问题，提出了一种改进的自适应遗传算法.对适应度函数、种群初始化、传统遗传算子进行了优化，并引入灾变算子，设计自适应变异，通过仿真证明了该算法的可行性.在利用机器人进行数据采集和预警作业时，为了使其更好适应复杂多变的实际环境，以及提高机器人作业时的效率，提出采取多模式人机协同控制，在实验中发现采用人机协同控制的机器人能够更好地完成作业，证明了该方法的有效性.