多层结构周期折减的规范设计与应用
吴轶雄
中国石油天然气管道工程有限公司沈阳分公司,辽宁 沈阳 110000
建筑结构的地震作用计算是结构抗震设计的重要组成部分,地震力是由地面运动引起的惯性力[1],其大小与结构质量、刚度密切相关。在结构设计中,房屋砌体填充墙的质量可以荷载形式代入计算,但填充墙对整体刚度的增大贡献无法直接体现,因此通常以结构刚度与周期的反比关系,以结构周期折减方式加以考虑。《高层建筑混凝土结构技术规程》(JGJ 3—2010)[2](以下简称《高规》)给出了周期折减系数的建议值,对于非《高规》适用的多层房屋结构,该参数的选取并无明确要求。我国每年仍大量建设有多层结构,因此领会关于多层结构是否执行周期折减的规范精神对结构的经济性、安全性具有重要的现实意义。
1 结构自振周期与水平地震作用
1.1 水平地震影响系数
结构地抗震计算的规范依据是《建筑抗震设计规范(2016年版)》(GB 50011—2010)[3](以下简称《抗规》),该规范确定的方法如下:
(1)底部剪力法。

式中:FEK为水平地震作标准值;α1为水平地震影响系数;Geq为重力荷载。
(2)振型分解反应谱法。

式中:Fji为j振型i质点水平地震作用标准值;Fxji、Fyji、Ftji分别为j振型i层x方向、y方向、转角反向水平地震作用标准值;α为地震影响系数;X、Y为水平相对位移;φ为相对扭转角;r为转动半径;γ为参与系数。
(3)时程分析法补充计算。多组时程曲线曲线的平均地震影响系数曲线应与振型分解反应谱法所采用的地震影响系数曲线在统计意义上相符。
以上三种计算方法均需利用水平地震影响系数α,该参数可由《抗规》地震影响系数曲线确定,如图1所示。
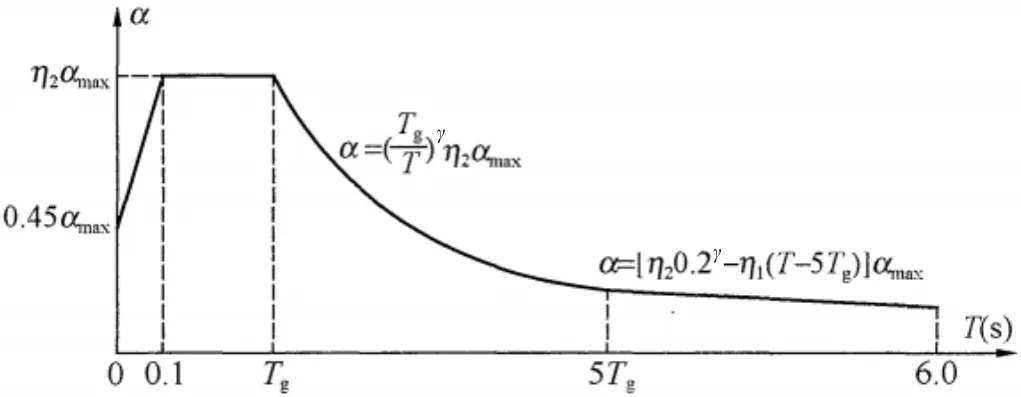
图1 地震影响系数曲线
影响曲线以0.1s和Tg为界,随自振周期增大,依次为上升段、水平段和下降段。
计算水平地震影响系数时,底部剪力法采用结构基本振型的周期,振型分解反应谱法采用不同振型的周期,但计算方法一致,均是根据该振型自振周期位于图1中横坐标的不同位置计算相应地震影响系数。结构自振周期对地震作用的影响,逻辑流程如图2所示。

图2 自振周期与地震作用逻辑流程
1.2 周期折减及相关规定
结构刚度k与自振周期T的关系,可近似取:

式中:k为结构刚度;T为自振周期;m为结构质量。
由式(4)可知,结构的刚度与周期呈负相关,同质量的结构,当刚度越大时,自振周期越短。在结构设计中,通常只进行主体结构的计算,当建筑中的砌体填充墙与主体混凝土墙柱为刚性连接时,结构的刚度不容忽视,其对结构的地震反应也不容忽视。为避免因填充墙结构刚度的增大,而引起结构自振周期的缩短,诸多资料均建议在计算中对结构自振周期进行折减,从而得出更合理的计算结果。
现行规范中,《高规》对周期折减系数给出如下参考值:框架结构的周期折减系数可取0.6~0.7;框架-剪力墙结构的周期折减系数可取0.7~0.8;框架-核心筒结构的周期折减系数可取0.8~0.9;剪力墙结构的周期折减系数可取0.8~1.0。
《高规》适用于10层及10层以上或房屋高度大于28m的住宅建筑以及房屋高度大于24m的其他高层民用建筑混凝土结构。对于非《高规》适用的多层结构,砌体填充墙对整体结构的刚度影响仍是真实存在的,由于现行《抗规》对周期折减尚未有明确要求,多层结构是否应进行周期折减,需结构设计者自行把控,而该参数可能影响地震作用计算,进而影响结构构件设计和整体安全。
1.3 高层结构折减必要性原理
根据《高规》适用条件及《建筑结构荷载规范》(GB 50009—2012)[4]附录F.2估算高层结构基本自振周期的最小经验值。
当以层数估算时,估算10层钢筋混凝土结构自振周期最小经验值为0.5s;当以高度估算时,根据《高规》表3.3.2限值,结构最大高宽比值为3,现以高度为24m、宽度为8m的结构估算自振周期最小经验值为0.4s。
以上计算均为理论最小值,根据场地特征周期不同,以上自振周期可能位于地震影响系数曲线水平段,也可能位于下降段。实际高层结构高度超过百米并不鲜见,其自振周期将远长于以上计算值。
如前文所述,水平地震影响系数由结构的基本自振周期确定,结构刚度增加则自振周期相应缩短,当结构自振周期位于地震影响曲线下降段时,自振周期T越短,则对应水平地震影响系数α越大,相应水平地震作用惯性力越大,因此自振周期实际值乘以小于1的参数,将得到更大的水平地震作用计算值,使结构设计偏于安全。即使最小周期以系数0.6进行折减,折减后周期仍大于0.1s,其水平地震作用较折减前增加或不变,因此对高层结构进行周期折减有其必要性。
2 计算示例
通过建立单层、多层结构模型并以周期折减系数0.6进行试算,验证该参数对计算结果的影响,总结其规律,探讨在实际结构设计中如何合理地选取周期折减系数。
2.1 方案概况
利用结构设计软件建立A、B、C、D四个框架模型,要求结构布置简洁、受力明确,结构立面、平面如图3、图4所示,这四个框架结构层数及高度均非《高规》适用范围。以这四个结构为例分析多层结构周期折减系数对计算结果的影响。

图3 框架立面图(单位:mm)
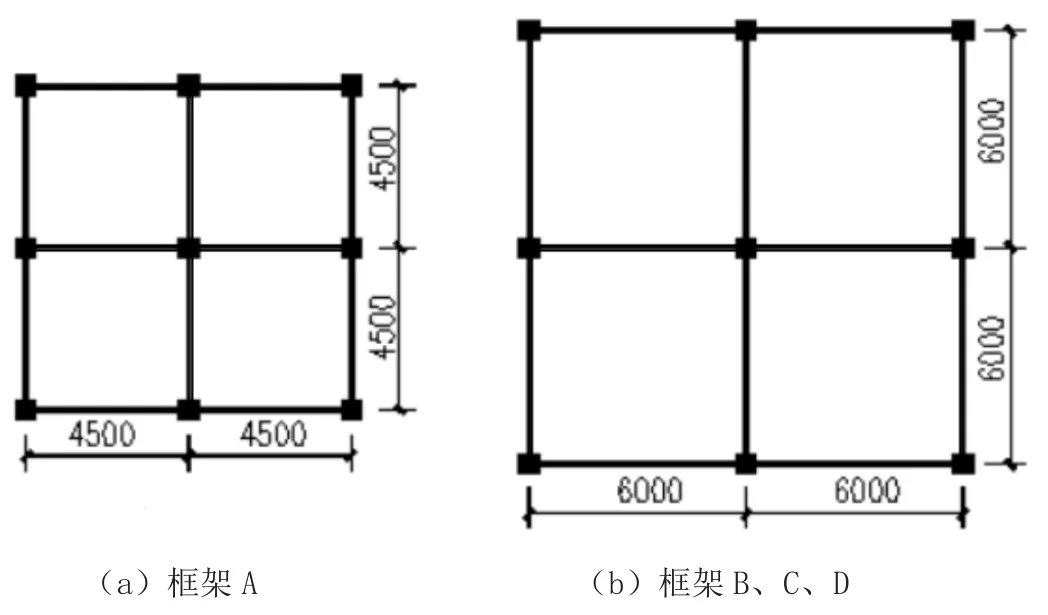
图4 框架平面图(单位:mm)
为检验周期折减对不同结构的影响,四个框架结构方案的建立采用类似结构形式,又考虑其自身特点:框架A柱距最小,梁线刚度最大,与其他框架布局形式一致;框架B、C、D平面布局均相同;框架D为多层结构,其余均为单层结构;框架C层高最高,其余框架层高相同。
四个简单框架所处场地、荷载及环境信息如下:设防烈度为8度(0.2g);第一组,Ⅱ类场地,特征周期Tg为0.35s;框架柱底嵌固标高为-1.0m,梁尺寸为300mm×500mm,柱尺寸为400mm×400mm,板厚为130mm;楼(屋)面恒、活荷载为2kN/m2,3m层高者梁上恒荷载为7kN/m,5m层高者梁上恒荷载为12kN/m,程序自动计算构件自重;均不计风荷载。
2.2 计算结果及分析
利用软件分别计算周期不折减及周期折减系数为0.6的情况,得出计算结果并提取部分指标如表1所示。分别对以上四个梁柱截面尺寸均相同的框架分析得出以下结论:

表1 结构计算主要指标
(1)四个方案中,框架A自振周期最短,其自振周期T为0.1563s位于影响系数曲线水平段,折减后的自振周期T=0.6×0.1563=0.09378<0.1,位于上升段,折减后的地震影响系数减小,因此折减后计算地震剪力减小。
(2)框架B折减后自振周期T=0.6×0.2027=0.12162,折减前后均0.1<T<Tg,位于影响系数曲线水平段,因此计算结果无差别。
(3)相比于框架B,框架C层高大,柱线刚度小,导致整体刚度小,周期略长于框架B,经计算,根据其自振周期确定的地震影响系数位于下降段,折减后位于水平段,因此折减后地震剪力增大。Tg÷T=0.35÷0.4402=0.795,0.1÷T=0.226,当折减系数为0.226~0.795时,折减后周期均位于水平段,计算结果均相同。在实际工程中,填充墙对刚度的贡献有限,周期折减系数不会低至0.226。
(4)框架D为多层结构,自振周期最长,折减前后自振周期均位于地震影响曲线下降段,因此折减后地震剪力增幅最大。
3 多层结构周期折减系数的应用建议
在实际设计中,会存在大量单层、多层房屋或塔架等非《高规》适用的框架结构,对于该类设计,文章提出如下建议。
(1)根据周期折减原理分析及建立模型试算验证,周期折减系数能够影响多层结构地震作用计算结果。其对结构的影响不局限于层数或高度,相同层数或高度的结构,根据其刚度不同,对周期折减的反馈亦不相同,并非折减后偏于安全。
(2)实际设计中可根据《荷规》附录F预估结构的自振周期进行第一次计算,得到结构实际周期,判断该周期位于《抗规》地震影响曲线中的位置。若自振周期T>Tg,位于地震影响曲线下降段,折减后地震影响系数变大,可参照《高规》或根据填充墙材料不同进行折减,代入程序进行第二次计算,自振周期越短,折减系数越适合取大值[5]。
(3)若结构自振周期0.1s<T<Tg,折减后的周期可能位于地震影响曲线的上升段,也可能位于水平段,地震影响系数减小或无变化,因此不宜或不需折减。虽然砌体填充墙对结构刚度的影响客观存在,但是抗震设计应以“概念设计”为主导,在“计算设计”理论尚不完全成熟的现实条件下,应按偏不利的计算方法进行计算。采用刚性连接的砌体填充墙在地震作用下,墙体与混凝土主体结构之间的有限连接(通常为拉结筋、墙顶斜砌砖)破坏后,结构刚度减小,周期增长,地震惯性力相应增大或无变化,按折减后的地震影响系数计算偏不安全或无变化。
(4)若结构自振周期T<0.1s,不可折减,理由同上。
(5)砌体填充墙与主体结构的连接强度不同,将影响填充墙在主体结构中的嵌固作用,当填充墙与主体结构采用柔性连接时,墙体嵌固较弱,可不考虑对整体结构刚度影响。《高规》条文说明中明确提出周期折减不包括采用柔性连接的填充墙。
综上所述,自振周期T>Tg的结构多层房屋结构建议进行周期折减,折减系数可参照《高规》执行,折减后结构计算偏于安全,对于自振周期T<Tg的结构,不建议进行周期折减,折减后偏于不安全或无变化。
4 结束语
周期折减系数由结构层数、层高、填充墙数量、场地信息等诸多因素综合决定,在计算过程中,应根据经验公式预估结构的自振周期。对于常见高层结构,可按《高规》建议值相应折减;对于多层结构,可按照《高规》建议折减值略放大进行计算。若无经验,可暂不折减进行计算,取得第一阵型周期后与场地特征周期Tg比较,若大于Tg则折减,不大于Tg则不进行折减。多层结构周期折减后的地震作用可能偏安全,也可能偏不安全或无影响,因此需要在实际设计中根据自身特点合理确定折减系数。

