三角恒等变换怎么“变”
2021-06-29 07:44章成尧
中学生数理化·高一版 2021年6期
章成尧
三角恒等变换包含三角函数的求值、化简和证明。下面归纳几种三角恒等变换的解题策略,帮助同学们灵活运用数学思想解决三角恒等变换问题。
策略一:变角
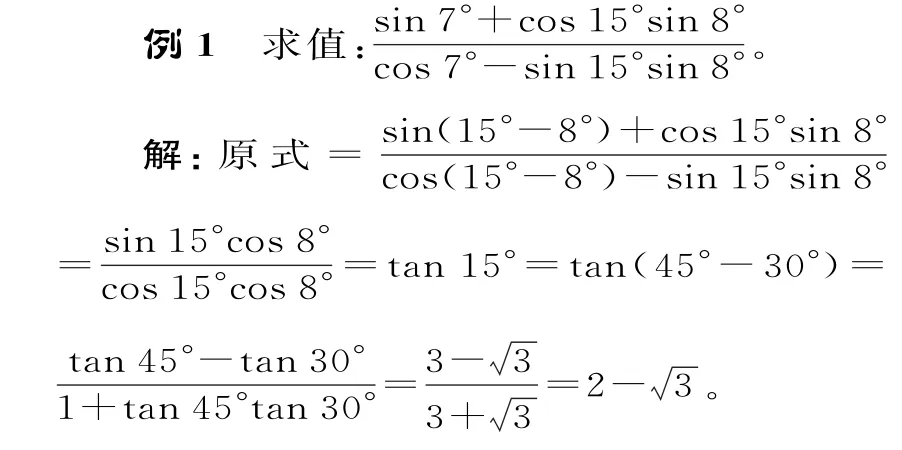
评析:三角恒等变换离不开角的变换,仔细分析条件与结论之间的角的差异,找出它们之间的相互关系,往往是解题的突破口。
策略二:变幂

评析:一般情况下,利用倍(半)角公式实施降次,借助“三角合成”达到“一次”的目的。
策略三:变名
例3 已知tanα,tanβ是方程x2-5x+6=0的两个实根,求2sin2(α+β)-3sin(α+β)cos(α+β)+cos2(α+β)的值。
解:由题意可得tanα+tanβ=5,

评析:三角恒等变换中,把不同名称化为相同名称是一种基本的变换策略,常见的有“切化弦”与“弦化切”。
策略四:变式

评析:根据结构式的特征,通过逆用两角和的正切公式是解答本题的关键。
猜你喜欢
小学生学习指导(高年级)(2022年10期)2022-11-04
音乐教育与创作(2022年6期)2022-10-11
中学生数理化(高中版.高考数学)(2021年11期)2021-12-21
数理化解题研究(2020年8期)2020-03-30
消费导刊(2017年24期)2018-01-31
中学生数理化·七年级数学人教版(2017年3期)2018-01-20
新高考·高二数学(2017年3期)2017-08-17
中学生数理化·七年级数学人教版(2017年12期)2017-02-15
中学生数理化·七年级数学人教版(2017年12期)2017-02-15
中学教研(数学)(2015年3期)2015-12-08

