点阵压气机叶轮的设计与3D打印仿真

张 源，李范春，贾德君

(大连海事大学 船舶与海洋工程学院， 辽宁 大连 116026)

随着航空工业与制造技术的发展，对叶轮性能的要求也不断提高.在保证叶轮具有所需气动性能的前提下，减少叶轮结构质量、增加飞行器有效搭载已成为叶轮设计的一个发展趋势.压气机叶轮是部分高速飞行器的最核心部件之一.高速飞行器飞行环境附近空气相对于飞行器速度一般在1.5 Ma (1 Ma=340 m/s)以上.当叶轮高速转动时，其尖端会产生激波，叶轮所受疲劳载荷会进一步加剧[1-2].对于轻量化航空压气机叶轮来说，其结构可靠性与安全性尤为重要.

应用点阵结构可以实现一般结构的轻量化设计[3]，且点阵结构有利于结构吸收碰撞能量，减少结构振动[4].因此，将点阵结构应用于压气机叶轮的轻量化设计中时，不仅可以减少叶轮质量，而且合理的点阵结构设计将使得叶轮具备吸收激阵能量的能力，从而减小由于周期性载荷引起的对叶轮的疲劳损坏.在满足气动性能与结构可靠性的前提下，金属点阵结构叶轮在航空航天领域将具有极可观的应用前景.对于多数现役飞行器的压气机而言，其叶轮可以通过例如铸造和机铣等传统加工工艺加工.尽管如此，这些传统机加工工艺仍不能够实现金属点阵结构叶轮的加工.

随着增材制造技术的发展，由于具备简单(不需要刀具、夹具及多道加工工序)、高效(较传统加工工艺加工周期更短)、复杂结构可加工性强(在一台设备上可以以高精度快速加工方式制造出多种复杂形状零件)等优点，金属3D打印技术正逐渐被广泛应用于各行各业[5-6].应用金属3D打印技术可以实现金属点阵结构叶轮的加工.

目前，研究人员通常基于实验方式对简单结构的金属3D打印工艺与被加工件的性能进行研究[7]，并总结出经验性能评估依据.但是，大量重复实验与测量会使得成本过大.应用实验方法研究复杂金属点阵结构叶轮的打印过程与打印后性能的可行性较差.然而，只有确保金属点阵结构叶轮具备生产可能性，才能将该型叶轮应用于实际.因此，有必要使用一种新方法对金属点阵结构叶轮的打印过程及打印后性能进行研究.在众多潜在可行的方法中，计算机辅助工程(CAE)技术就是其中之一.

在过去的几十年间，CAE技术已广泛地应用于航空相关领域.该技术的应用可以缩短工作周期，降低工作成本.在轻量化点阵结构及其增材制造的研究工作如疲劳分析[8]、制备设计[9]以及性能分析与优化设计[10-12]中，CAE方法也得到了广泛的应用.尽管如此，由于一些原因，仍需要进行一些额外的研究工作为金属点阵结构叶轮的增材制造作业提供技术参考.首先，打印后压气机叶轮存在残余变形以及残余应力，这两个值将直接影响打印结果的好坏.而影响这两个指标的因素众多，包括激光功率、激光走速、激光宽度、铺粉层厚、基板温度等机器参数以及粉末材料属性、叶轮几何形式等叶轮自身属性.目前业内的相关研究工作的焦点是规则几何形状被加工件打印后的性能评估.这些研究工作对金属点阵结构叶轮这样复杂结构的增材制造作业提供的参考是非常有限的.其次，在压气机叶轮的3D打印作业中，其成型过程是一个合金粉末不断快速熔化而后凝结的过程.在此过程中，加热温度高低以及冷却速率快慢都会对熔融态粉末晶相组织的形成造成影响，从而使材料层间产生较高的残余应力，引起叶轮结构破坏，甚至在打印过程中出现开裂.目前有关金属3D打印的研究主要侧重于打印后被加工件的性能，考虑被加工件打印过程中性能的研究是鲜有的，而有关金属点阵结构叶轮3D打印相关工作则是空白.

基于此，本文基于八角桁架点阵结构，采用CAE技术对金属点阵压气机叶轮进行轻量化设计，对其在不同功率下的打印过程及打印性能进行计算分析.此外，采用SLM280型金属3D打印机对压气机叶轮进行增材制造，并应用3D扫描技术获得叶轮几何文件.采用基于热应力分析的有限元方法对金属点阵结构叶轮3D打印作业进行模拟，将通过计算获得的打印后叶轮几何文件与通过扫描获得的叶轮几何文件进行对比，初步验证数值方法的可行性.随后，本文应用有限元方法计算了不同激光功率下金属点阵结构叶轮与实心叶轮打印过程中的残余应力及残余变形的变化，并对变化趋势进行了对比分析.最后，对比分析了两种叶轮可加工性的优劣，同时对打印作业参数设计提供技术参考.

1 基于SLM激光粉末熔融过程热力学分析

为研究增材制造过程热-力学行为以及描述这些行为的数值计算方程及计算方法，首先，采用Galerkin方法将物理控制方程转化为弱形式方程.能量平衡方程为热问题的控制方程，应力平衡方程为力学问题的控制方程.通过弱形式控制方程可以导出被加工件节点位移解向量U及残余向量R.从计算初始U0开始，Newton-Raphson方法应用于迭代过程的形式为

(1)

式中,i和i+1分别为前一迭代步和当前步的迭代步的序数.每一个时间步中，前一时间步的解都将作为当前时间步的计算初始值.迭代是一个基于生死单元逐层进行的过程，未激活层设置为死，激活层设置为生，逐层激活.在工程热力学问题分析中，拉格朗日参考系下准静态热弹塑性过程有限元公式得到了广泛应用[13].该方法假设热分析是瞬态的，而弹塑性分析是准静态的.在例如焊接及热辅助成形等许多热弹塑性工艺分析中，通常假定力学变量与热学变量之间存在弱耦合关系，即假设温度分布独立于应力和应变.因此，在进行模拟3D打印过程的数值计算时，首先进行传热分析，并将温度分布作为力学分析的导入载荷.

1.1 瞬态热分析

对于一个等密度各向同性体，设其密度为ρ，比定压热容为cp，其控制方程可表述为

(2)

式中：T为节点温度；t为时间；q为热流；X为相对参考坐标向量；Q为热源.

此处一个必要初始条件为

T0=T∞

(3)

式中：T0为初始温度；T∞为环境温度.方程的边界条件为

T(X,t)=Tp(X,t)

(4)

qs(X,t)=qp(X,t)

(5)

式中：qs(X,t)为面热流；Tp(X,t)和qp(X,t)分别为规定温度向量和与温度相关的表面热通量.表面对流换热和表面辐射换热过程对应的表面热流量qp(X,t)的形式为

(6)

式中：h为对流系数；ψ为热辐射率；δ为玻耳兹曼常数.零件的热流分布由傅里叶热传导方程进行描述：

(7)

式中,k为导热系数.焓变率的形式为

(8)

式中,H为焓值.联立等式(2)、(7)、(8)可得：

(9)

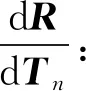
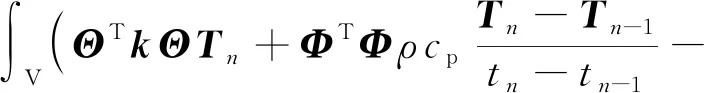
(11)

(12)

式中：V和A分别为单元体积分域和面积分域；T为单元温度节点向量；Tn和Tn-1分别为tn时刻与tn-1时刻对应的温度；Φ与Θ分别为温度算子与温度梯度算子；在下文中，下标n或n-1均表示在tn和tn-1时刻所对应的物理量.这里：

T=ΦT

(13)

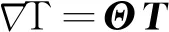
(14)

以上方程的求解需要初始条件、热输入模型以及温度边界条件.初始条件可设定为基板温度、环境温度或预热温度.热输入模型可以由面热流输入模型或体输入模型进行描述.由于3D打印轮内部并不存在体热源，因此本文采用面热流输入模型对3D打印热输入模型进行刻画，其边界条件通常设置为环境温度和基板温度.在本研究中，基板温度为200 ℃，环境温度约为45 ℃.对于金属3D打印，热流输入模型由椭球热流密度输入模型进行刻画较为准确.设椭球中心为O(0, 0, 0)，半轴分别为a、b、c.为方便求解，将直角坐标系圆点设为椭球中心，规定熔池深度方向为y向，熔池移动方向为x向，z向为x-y面外法线方向.其热流输入可由下式进行描述：

(15)

式中：υ为融化速度；τ为滞后系数，用于定义t=0时热源位置.

1.2 力学分析

在进行热分析之后，需要在热分析基础上进行力学分析，以获得材料沉积过程中零件的机械响应.将热分析结果作为热载荷输入到力学模型中.应力平衡控制方程可由下式进行描述：

(16)

式中：B为二阶应力张量；b为体力.对于边界为A的同一材料，其边界条件由以下两式进行描述：

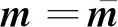
(17)

(18)

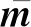
总应变ε可以由式(11)进行描述：

ε=εe+εp+εT

(19)

式中：εe、εp及εT分别为弹性应变、塑性应变和热应变.弹性应变可由应力-应变关系求得.初始条件为：

u=u0

(20)

εp=εp0

(21)

εq=εq0

(22)

式中：u为位移矢量；εq为等效塑性应变，下标0表示t0时刻对应的物理量.应用离散化方法可以得到在tn时刻的应力表述：

σn=σn-1+Δσ

(23)

分别在tn-1和tn两个时刻求解式(19)，可得

Δσ=cpn[Δε-Δεp-ΔεT]+Δcpn-1εe

(24)

式中：cpn为tn时刻的比定压热容.

Δε=Φ(Un-Un-1)

(25)

热应变由下式进行计算：

ΔεT=(εTn-εTn-1)i=

(26)

(27)

式中：a′为热膨胀系数；Tref为参考温度.

采用Von-Mises屈服准则和Prandtl-Reuss流动准则计算塑性应变：

f=σm-σy(εq,T)≤0

(28)

(29)

(30)

式中：f为屈服函数；σm为最大应力；σy为屈服应力；l为流向量.

参考热分析方程，应用方程的弱形式以及有限元离散方法，可以得到单元残余项：

(31)

式中：GVe为单位体积Ve上的高斯点；J和j分别为单位体和单位面上的Jacobian分量；W和w分别为单位体和单位面上的Gaussian加权.

2 轻量化点阵叶轮3D打印工艺过程数值研究

本节将基于有限元方法对点阵轮和实体轮3D打印过程进行数值模拟.

首先，基于有限元方法计算点阵轮与实体轮在标况(规定表1参数下为标况)下的残余变形，并分别获得点阵轮和实体轮变形后的表面几何文件.同时，利用SLM280型金属3D打印机打印出相同参数下点阵轮，用激光3D扫描仪扫描获得打印点阵轮表面几何文件.利用曲面拟合方法分别将打印模型表面几何文件、数值结果表面几何文件与原模型几何表面进行拟合对比，证明数值模拟方法可行性.

在数值模拟方法可行的前提下，对实心轮和点阵轮在不同功率下的残余变形及残余应力进行计算，基于计算结果，对不同功率下点阵轮与实体轮打印中的残余应力及残余变形进行分析，对打印工艺设计提出参考意见.

2.1 SLM粉末熔融金属3D打印数值模拟方法可行性验证

保证方法可行性是进行下一步研究的前提，本节将对数值模拟方法研究金属3D打印过程可行性进行验证.

2.1.1数值模拟前处理及仿真 金属3D打印仿真前处理阶段主要分为模型的建立、模型的三角化、模型及支撑结构的导入和网格生成4步.TiAl6V4合金具有较好的力学性能并被大量应用于航空航天等领域，是3D打印常用的材料之一[14].本文研究所用的实体模型及点阵结构材料均选择TiAl6V4合金.目前常用到的桁架式的点阵结构有10种类型，如图1所示.其中，由立方体晶格变形所得的晶格形式为(1)～(6)，基于双棱锥晶格结构变形所得的晶格形式有4种，分别为(7)～(10).在对叶轮内部点阵结构进行3D打印时，由于内部点阵结构添加支撑会导致打印完成后支撑无法去除，所以，打印加工需要保证点阵横梁能够在无支撑条件下实现自支撑，从而保证点阵在打印时不发生塌陷.设单个标准立方胞元的边长为L，如图2所示，常规立方点阵胞元[图2(c)]由标准立方胞元[图2(a)]去除多余材料[图2(b)]获得.图1中的所有点阵结构也可以由相同的方法制得.对于由立方体晶格变形所得的 (1)～(6)六晶格结构和(8)、(9)两种双棱锥变形所得结构，其最大水平杆件悬空长度均为L，而对于由相同标准立方胞元制得的八角桁架点阵胞元 (图1(10))，其最大水平杆悬空长度则只有0.707L，这意味着八角桁架点阵通过3D打印技术将更容易制备.其次，八角桁架点阵由多个6杆三角形刚架构成，其结构稳定、传力直接、节点受力，机械性能优异[15]，同时具有优异的热传导性和流体流动性[16].图1(7)中的双锥型点阵胞元单根杆件的最大悬升角均为45°， 这意味着其打印时也能实现自支撑，但是由于其刚度不足，因此不宜选用.

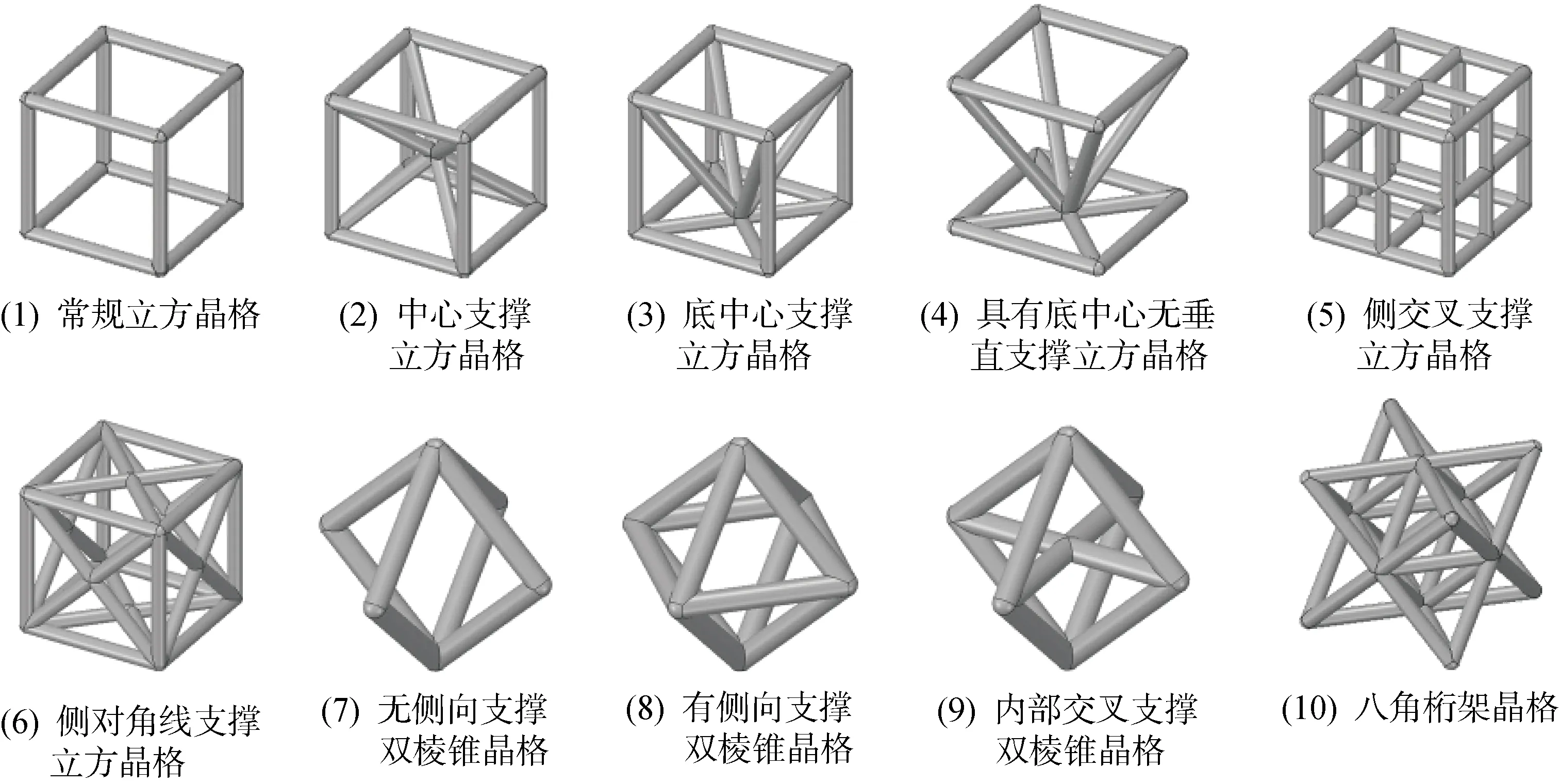
图1 常用桁架式点阵结构胞元Fig.1 Cell of commonly used truss lattice structure

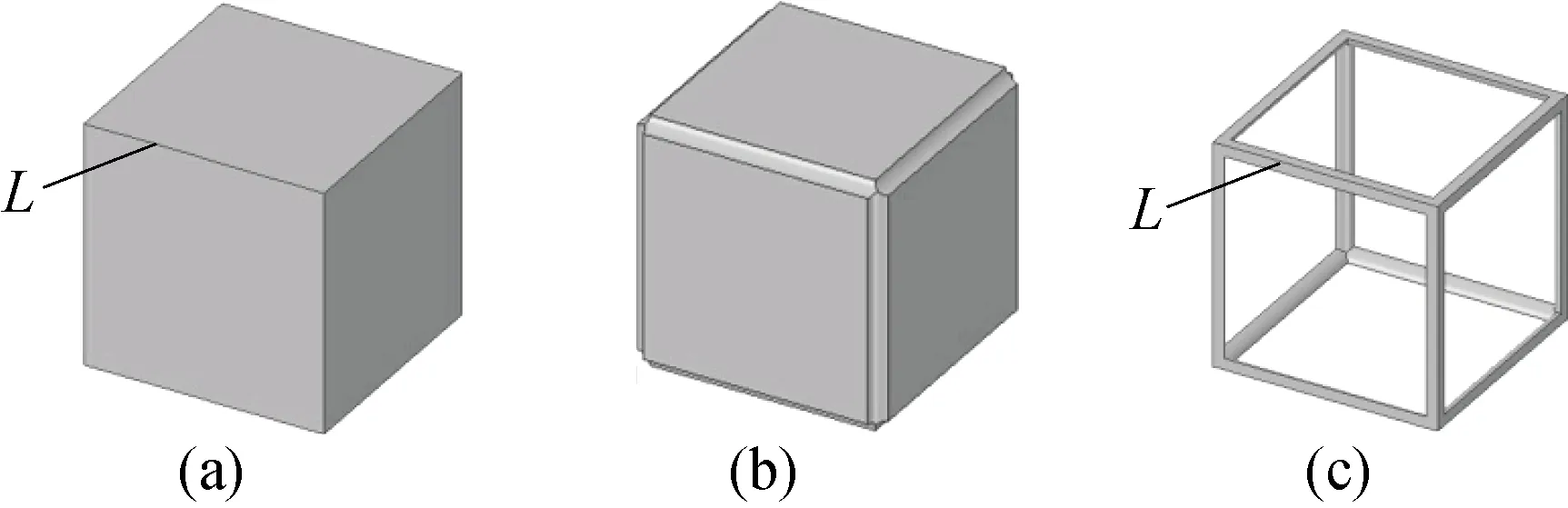
图2 由标准立方胞元减材获得的简单立方晶格Fig.2 Simple cubic lattice obtained by reduction of standard cubic cell

基于以上分析，本文所用点阵选择八角桁架点阵结构，其有效机械性能以及其弹性和塑性屈服模式见文献[17].本文所用单个晶格尺寸为4 mm×4 mm×4 mm，点阵梁直径为0.4 mm，单个晶格填充率为11.4%.将点阵结构镶嵌在叶轮中得到点阵轮模型.由于3D打印机识别的文件为三角体文件，因此需要对实体模型三角化得到三角体模型.将三角体模型导入仿真软件，同时导入支撑结构，生成网格，完成前处理操作，如图3所示.实心轮前处理过程类似，不予赘述.

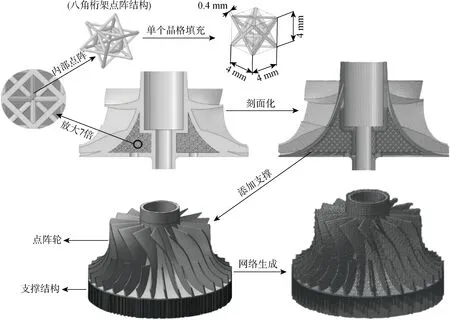
图3 点阵轮分析前处理过程Fig.3 Pre-treatment process of lattice impeller analysis

在点阵轮及实心轮仿真前处理过程完成之后，进行初步仿真结果计算.仿真计算的主要步骤如图4所示.其中，有限元网格依据铺粉层厚的不同进行划分，需要保证计算精度与仿真时间的合理性.初始条件及边界条件的定义，即激光功率、走速、铺粉厚度及基板温度等基本参数的设置在热流模型的输入过程进行.有限元计算过程需要确立热流输入模型，然后基于瞬态热分析和热固耦合分析实现叶轮热应力及热应变的计算.目前生死单元仿真技术被广泛应用于变质量问题的计算[18]及焊接问题的仿真计算[19-20].如式(1)所述，整个热力学的计算过程是一个基于生死单元的逐层迭代的过程，不同层的计算过程中网格逐层激活，最后的仿真结果是逐层结果的叠加.由于网格事先划分完成，生死单元技术只是被用作单元激活，因此迭代过程无需重新划分网格.

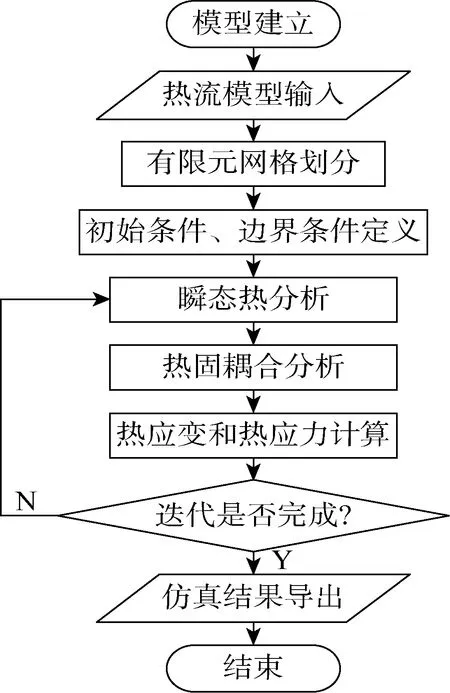
图4 仿真过程的主要步骤Fig.4 Main steps of simulation process

2.1.2金属增材制造能量沉积原理 金属3D打印过程是激光粉末在激光加热下熔融再凝固的过程，如图5所示，图中v′为激光走速，局部输入过大的热流而周围温度较低.局部的材料势必要向外膨胀，而周围材料膨胀变形小于热源输入点的材料，从而限制了热源输入点材料的变形，因此产生较大的热应力(残余应力).金属粉末在输入热量Q的作用下，形成金属熔池，熔池的加热及冷却过程都直接影响着打印零件的变形与应力，而能量的输入直接影响熔池的大小、深度，进而影响零件的成型性能.

图5 粉末在激光下形成熔池Fig.5 Powder forming molten pool under laser

3D打印的仿真过程通过添加移动热源的方式实现系统的能量输入，采用热流密度作为热源.在不考虑粉末颗粒几何参数的条件下，单位体积单激光能量输入计算式为[21]

(32)

式中：P为激光功率；d为扫描线间距；μ为铺粉层厚.结合式(15)可以得到系统的热流输入模型.表面烧结温度与工艺参数间的关系可描述为

(33)

式中：η为耦合效率；TS为表面融化温度.

点阵轮与实心轮变形仿真结果如图6所示，图中ur为残余变形.导出图6所示的变形体几何文件.此处有几点需要解释说明：①叶轮轮毂底盘处存在较大的横截面积，对于3D打印，结构较大的横截面积尺寸意味着较大的热应力和残余应力且结构容易产生翘曲.由于残余应力的存在，在支撑和基板结构去除以后，由于缺少基板结构的抗变形拉力，残余应力被释放，从而会产生一边变形值较大，一边变形值较小的情况.图6所示的变形分布结果能够较好地说明仿真结果的准确性.②图中max表示整个仿真过程(包括材料堆叠过程、基板移除过程及支撑移除过程)所产生的最大变形，在保证支撑及零件无损坏前提下，通常此最大值出现在基板移除或支撑移除过程.

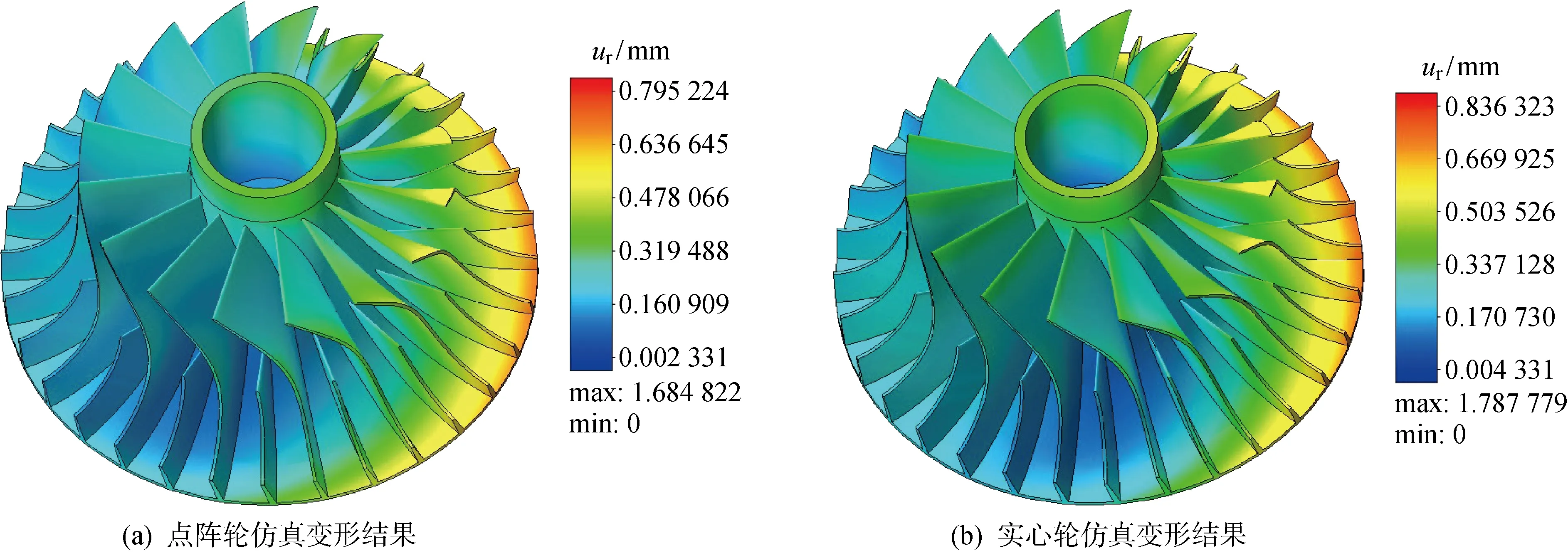
图6 点阵轮与实心轮仿真变形结果Fig.6 Simulation results of deformation of lattice impeller and solid impeller

2.1.3金属3D打印点阵轮实体结果的获得 要验证仿真结果是否可行，需要对一个实体模型进行打印.本文选取SLM280型激光粉末熔融金属3D打印机对点阵轮进行打印，打印过程的主要参数设置为：激光功率为275 W，激光走速为1.1 m/s，层厚为0.03 mm，扫描间距为0.12 mm，激光初始偏转角为15°，层偏转角为67°.

点阵轮实体模型的打印过程如图7所示.SLM280型金属3D打印机读取的文件为三角化文件，因此需要对原模型进行三角化操作，在对原模型进行三角化操作后，切片生成扫描路径，激光将沿着扫描路径进行合金粉末熔融过程.扫描过程逐层进行，粉末材料逐层堆叠.在进行去除支撑及基板等后处理操作后得到点阵轮的打印结果，此时，叶轮的底面已经通过铣削工艺进行过加工，以降低叶轮底部粗糙度.直接打印的叶轮的粗糙度为6.3 μm，铣削叶轮的粗糙度为1.6 μm.

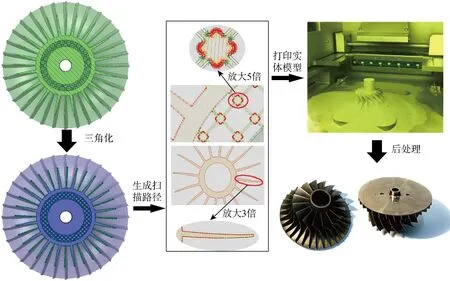
图7 点阵轮打印过程Fig.7 Printing process of lattice impeller

2.1.4表面几何文件获取及曲面拟合结果对比 点阵轮和实心轮的表面几何文件通过导出图6(a)、 (b)的仿真变形文件得到.导出时变形比例因子设置为1,即按照1倍变形比例导出仿真变形结果.实际打印点阵轮的表面几何文件则是通过手持式激光3D扫描仪扫描得到.手持式激光扫描仪的扫描过程如图8所示，其中，图8(a)为操作人员正在进行扫描操作，图8(b)为计算机中扫描几何文件的生成.

图8 手持式激光扫描仪扫描过程Fig.8 Scanning process of handheld laser scanner

图9为几种叶轮表面的三角化几何面，其中，图9(a)为实际打印模型扫描所得的表面几何，由于手持式激光扫描设备会造成局部缺失及操作时产生的误差， 扫描形成的刻面化主体叶轮边缘及光滑曲面存在少量残缺面，即图9(a)中的白色小孔.图9(b)和(c)分别为打印过程仿真结果中导出的点阵轮和实心轮变形模型表面几何.与实验扫描获得文件不同，导出的仿真刻面体表面没有残缺.由于大量扫描非残缺区域可以与仿真导出文件进行比较，因此，点云几何文件的少量残缺不影响两个结果的比较.由于本文应用的扫描设备只能够获得叶轮上表面几何数据，故本节主要针对两个模型上表面进行比较.在未来的研究中，可以采用X射线对叶轮内部点阵进行数据提取，进而与仿真结果进行比较.

图9 叶轮表面三角化几何Fig.9 Surface triangulation geometry of impeller

在获得叶轮表面的三角化结果后，采用曲面拟合方法对三角几何与设计模型表面进行拟合比较.图10(a)、(b)及(c)分别对应打印轮、点阵轮仿真及实心轮仿真设计拟合斜视图，图中dr为拟合的相对偏差.对比发现，点阵轮打印结果与仿真结果存在一致的变形分布.二者叶轮底面边缘与叶片顶面均会产生少量变形，变形范围在0.25 mm内.二者导流叶片位置变形均较小，大叶片边缘产生的变形较大，仿真结果相较于实际打印结果仅在大叶片边缘存在较小差异，整体上仿真值与实际测量值具有较好的一致性.因此，可认为本文利用数值方法模拟叶轮的实际打印作业过程是有效的.

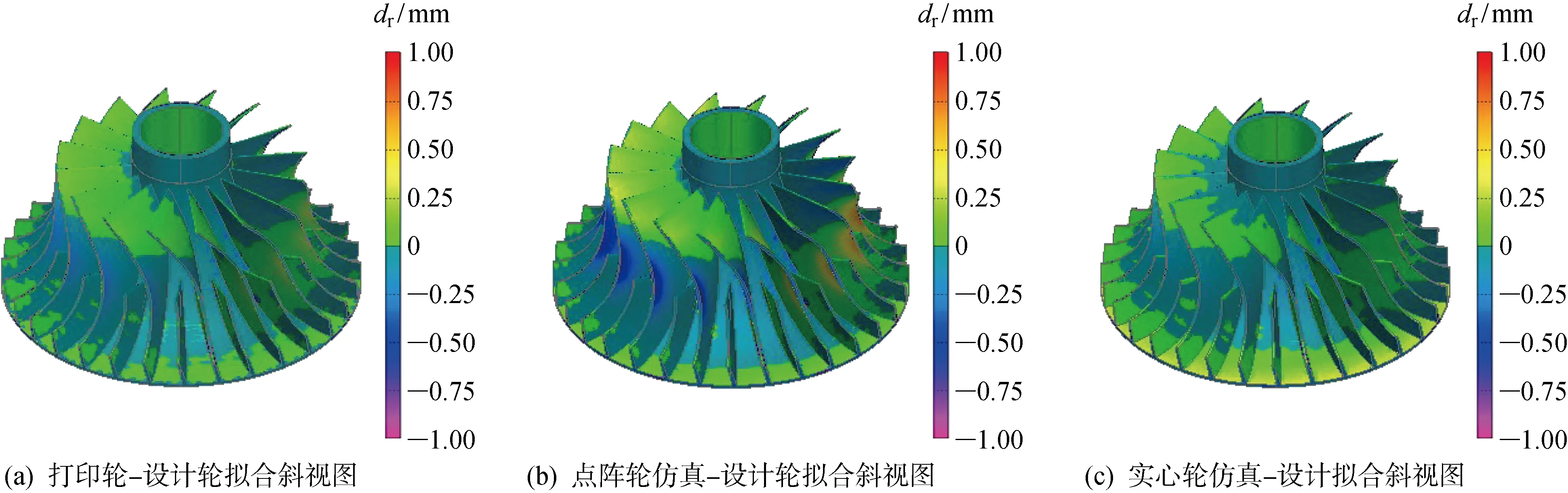
图10 曲面拟合结果对比Fig.10 Comparison of surface fitting results

2.2 点阵轮与实体轮不同激光功率下的残余变形及残余应力

本文基于SLM280型激光粉末融床金属3D打印机进行打印参数选取.在功率范围为150～300 W区间对点阵轮及实体轮打印过程进行研究，其中，相邻功率间隔25 W.假定2.1.3节中的给定工况为标准工况.

2.2.1点阵轮与实心轮打印过程时域结果 选择3组不同功率下打印过程做时域分析，其基本参数设置如表1所示.

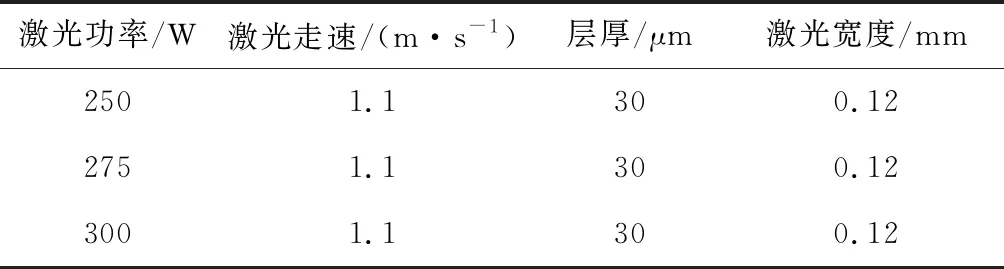
表1 不同激光功率下的打印参数Tab.1 Printing parameters at different laser power values

图11、12分别为3组功率情况下的最大残余变形和最大残余应力时域结果，图13显示了关键层在仿真过程的层分布情况.图中：σrmax为最大残余应力，urmax为最大残余变形，lN为层数.此处的层为网格层数，而非粉末层数.粉末层厚为30 μm，网格层厚为1 mm.

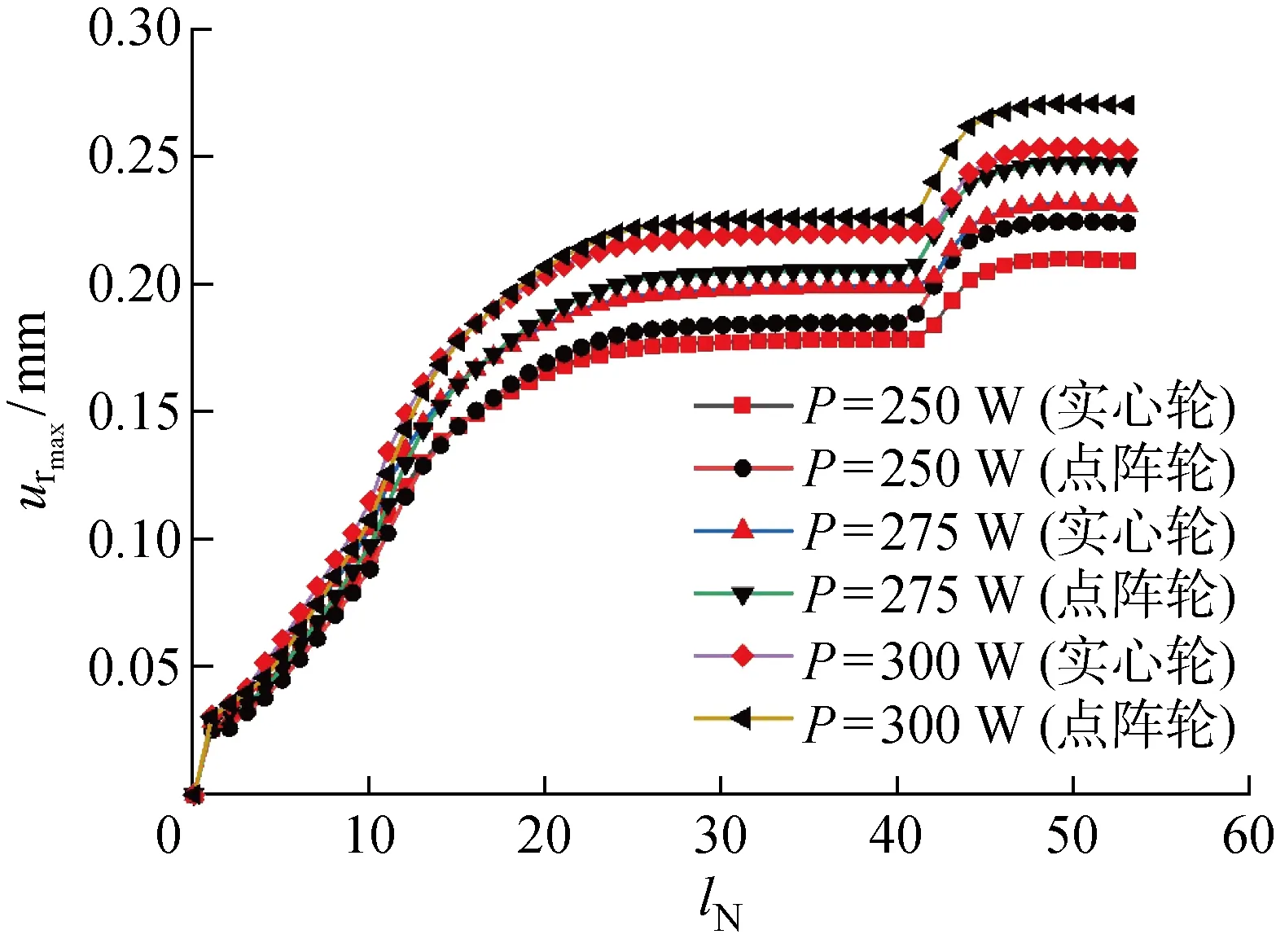
图11 不同功率下最大残余变形Fig.11 Maximum residual deformation at different power values

图12 不同工况下最大残余应力Fig.12 Maximum residual stress under different working conditions

图13 层分布Fig.13 Layer distributions

由图11可知，不论是点阵叶轮还是实心叶轮，在以上3种功率工况下，层变形都随堆叠层数增加而增加，且二者的变形最大值与层数之间均存在一个非线性关系，点阵轮与实心轮之间的这种非线性变形具有相同分布趋势，再次验证前文所述的层变形是一个逐层累加的过程.为方便说明，将部分层位置在图13中进行标注.在表1工况下，点阵叶轮变形都主要在前31层(恰好完成点阵结构打印)，而实心叶轮的最大变形增加主要集中在25层之前(轮轴轴孔变大位置).不论是点阵轮还是实心轮，在打印叶轮的前11层过程中(支撑结构打印完成之前)，叶轮变形增长最快.点阵叶轮在打印至31～40层(点阵打印结束至叶轮顶面下方)时，叶轮变形基本不变，实心叶轮则在打印至25～41层(轮轴轴孔变大处至叶轮顶面下方)时，叶轮变形保持基本不变.随打印层数增加，点阵轮和实心轮均会出现第2次最大变形增长区，其中点阵轮该区域出现在40～44层(叶轮顶面下方至叶轮顶面)，实心轮该区域出现在41-45层.最后点阵轮和实心轮最大残余变形都会再次达到一个稳定值.从变形的整体趋势来看，在以上3种功率下，点阵轮和实心轮的变形曲线均存在1个交点，该点之前均为实心轮层最大变形大于点阵轮，该点之后均为实心轮层最大变形小于点阵轮.此外，无论是对于点阵轮还是实心轮，功率增大，层变形增大.如式(32)，功率增大导致熔池能量输入的增加，进一步使3D打印过程的局部热流输入增大，而此时材料周围的温度较低，局部材料势必向外膨胀，而周围材料的膨胀变形小于热源输入点的材料变形，因此产生较大的热应力，当热源在结构边缘处没有周围强力约束时将产生较大变形.

对比图12，发现在材料堆叠过程中，点阵轮与实心轮之间最大层应力差主要出现在前几层，随后点阵轮与实心轮应力基本趋于一致.点阵轮的前几层最大残余应力均大于实心轮.在堆叠过程中，每一层的加热都是反复进行的，下一层材料堆叠的同时会对上一层材料进行加热.因此，后面材料的堆叠会对前面材料的堆叠过程造成影响，这种影响导致了点阵轮和实心轮在11层之前，最大残余变形和最大残余应力分布也会有所不同.此外，功率的增大也会引起最大残余应力较小增长.

2.2.2不同功率下点阵轮与实心轮打印结果分析 图14为不同功率下点阵轮与实心轮的残余变形最大值及残余应力最大值比较.比较主要分为3个部分：基板移除前、基板移除后和支撑移除后.

图14 不同功率下被打印件的残余变形最大值及残余应力最大值Fig.14 Maximum values of residual deformation and residual stress of printed part at different power values

由图14(a)可知，基板未移除时，点阵轮和实心轮的变形均随激光功率的增大而线性增大，且点阵轮最大残余变形增大的速率稍大于实心轮.基板移除后，由于内部应力的释放，实心轮和点阵轮的最大残余变形都会大幅增加，实心轮增大相较于点阵轮更多.实心轮整体上满足最大残余变形随激光功率的增大而线性增大.点阵轮在该过程中的最大残余变形在功率较大情况(≥150 W)下均小于实心轮.支撑移除后，点阵轮和实心轮的最大残余变形都会进一步增大，但是实心轮在所有功率下的增大都极小(最大不超过0.02 mm)，而点阵轮增大则较多(约0.1 mm).

由图14(b)可知，基板未移除时，实心轮的最大残余应力随功率增大呈指数增长趋势，而点阵轮的最大残余应力随功率增大呈线性增长，当功率较小时(≤175 W)，点阵轮的最大残余应力与实心轮基本保持一致.当功率逐渐增大(175～275 W)，实心轮最大残余应力小于点阵轮.当功率进一步增大(>275 W时)，实心轮最大残余应力大于点阵轮，并且增长率逐渐变大.基板移除后，内部应力被释放，点阵轮和实心轮最大残余应力都降低，降低率随功率增大逐渐减小.实心轮的最大残余应力随功率增大而呈非线性增长，增长率随功率增大降低，点阵轮的最大残余应力随功率增大线性增大.功率小于175 W时，点阵轮的最大残余应力大于实心轮，功率大于175 W时，点阵轮的最大残余应力小于实心轮.支撑移除后，实心轮的最大残余应力随功率的变化趋势与支撑移除前基本一致.点阵轮的最大残余应力随功率的变化趋势仍然保持线性，增长速率较支撑移除前有所增大，250 W之前，支撑移除前最大残余应力大于支撑移除后，功率大于250 W时，支撑移除前最大残余应力小于支撑移除后.

通过以上分析，发现支撑结构的移除对实心轮的变形及应力影响不大，对点阵轮的变形及应力影响较大，但是支撑移除并不会造成其最大残余变形分布趋势的变化，只会造成整体分布趋势的上移.

2.3 点阵轮与实心轮打印结果比较

目前，针对点阵轮3D打印过程的研究基本还处于空白，从增材角度对实心轮的研究也尚不完善.相较于实心轮，点阵轮在一定程度上更具加工优势，但是这种优势并非无限制的.相对偏差反映了点阵轮与实心轮之间残余变形或残余应力的相对差值，计算式为

当打印参数发生改变，点阵轮同实心轮的相对偏差也会随之改变.为使点阵轮相较于实心轮的打印优势最大化，有必要对不同打印参数下点阵轮与实心轮的残余变形与残余应力的相对偏差进行分析.本文对不同激光功率下点阵轮和实心轮的残余变形与残余应力的相对偏差结果进行定量比较.表2定量反映了点阵轮与实心轮在打印完成时，不同激光功率下的残余变形及残余应力的相对偏差值.

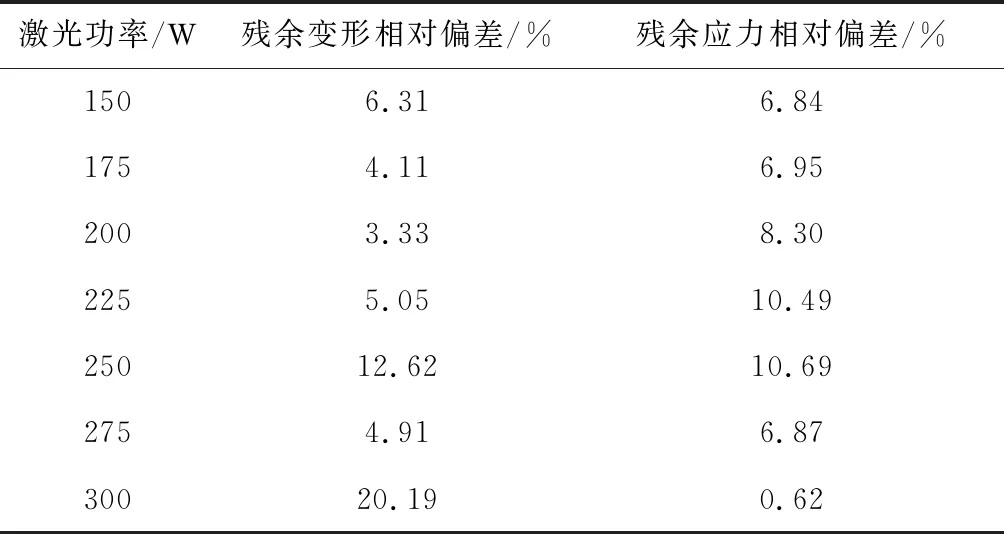
表2 不同激光功率下点阵轮与实心轮的残余变形与残余应力的相对偏差

由表2可知，当以激光功率作为变量时，功率为300 W时残余变形相对偏差最大值为20.19%，当功率为250 W时，残余应力偏差最大值为10.69%.

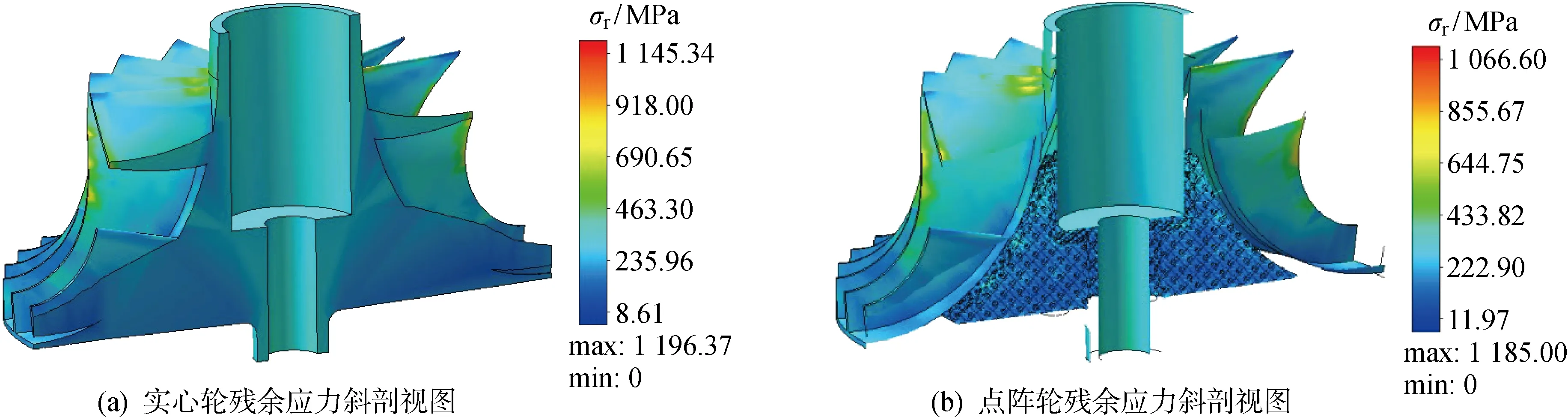
图16 点阵轮和实心轮支撑移除后残余应力Fig.16 Residual stress of lattice impeller and solid impeller after support removal

图15、16分别为点阵轮和实体轮在支撑移除后的残余变形及残余应力分布，图中σr为残余应力.对比发现二者最大残余变形总体分布趋势大致相同，叶片上边缘存在较小差异，各处分布幅值不同，二者最大残余应力分布趋势基本一致.

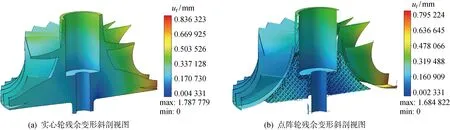
图15 点阵轮和实心轮支撑移除后残余变形Fig.15 Residual deformation of lattice impeller and solid impeller after support removal

4 结论

(1) 本文将八角桁架结构点阵应用于压气机叶轮设计中，对于单个胞元填充率为11.4%的点阵轮，其质量相对于原设计轮可降低23.5%.

(2) 结合有限元仿真技术，对点阵轮和实心轮的最大残余变形进行了计算，并利用SLM280型金属3D打印机对点阵轮进行了打印，通过曲面拟合方法，对实际打印点阵轮表面几何结果与仿真点阵轮的表面几何结果进行了比较.发现仿真预测变形分布与实际打印变形分布具有大致相同的分布趋势，仿真结果与实际打印结果吻合良好，充分说明采用有限元方法研究金属3D打印过程的有效性.

(3) 不同激光功率下，叶轮层变形分布保持一致，幅值不同，基板未移除时，点阵轮与实心轮最大残余应力均随功率增大而增大，最大残余变形随功率增大变化较小，此时，实心轮变形均小于点阵轮.基板移除后，实心轮和点阵轮的最大残余变形均大幅增加，实心轮增速较快，此时，实心轮变形均大于点阵轮.支撑结构的移除对实心轮的变形及应力影响不大，对点阵轮的变形及应力影响较大，但是支撑移除并不会造成其最大残余变形分布趋势的变化，只会造成整体分布趋势的上移.

(4) 在本文所有工况下，点阵轮的应力及变形幅值均小于实心轮.当激光功率为300 W，其余参数保持标况时，点阵轮残余变形最多可比实心轮小20.19%.当激光功率为250 W，其余参数保持标况时，点阵轮最大残余应力最多可比实心轮小10.69%.这意味着点阵轮比实心轮具有更好的3D打印性能，点阵轮在打印完成时具有更好符合原始设计的表面形状，进而可以保证更好的气动性能.