基于非局部Biot理论的平面波作用下饱和地基动力响应

王 宁，丁海滨，童立红，蒋亚龙

(1. 华东交通大学 江西省岩土工程基础设施安全与控制重点实验室，南昌 330013； 2. 江西省地下空间技术开发工程中心，南昌 330013)

关于弹性波传播至两种介质交界面的反射及折射问题，国内外学者已经做了充分的研究[1-3].但以往对于饱和土中弹性波传播问题的研究基本都是基于经典Biot理论[4].然而，Biot理论的建立是基于波长远大于饱和土中的孔隙尺寸的假设，但理论[5-8]及试验[9-10]研究均表明，在高频下，波长远大于孔隙尺寸的假设已不再成立，此时，孔隙材料的孔隙尺寸对波传播特性具有显著的影响.此外，波的传播会引起土颗粒的运动，由此会导致土颗粒产生惯性力(孔隙动应力)，显然此惯性力随入射频率的增加而增大，而Biot理论假定孔隙尺寸为常数.因此，其理论中未考虑孔隙尺寸及孔隙动应力对波传播特性的影响.

为解决上述问题，Chakraborty等[11]结合经典非局部弹性理论[12]和Biot理论[4]预测了饱和多孔材料中波的传播特性，但其由于考虑了流体的非局部效应，对Biot理论进行过修正，而使其预测结果与实验结果产生一定的偏差.Tong等[13]摒弃了流体部分非局部效应，提出了仅考虑土骨架非局部效应的非局部-Biot理论模型，分析了饱和土中波速的传播及其衰减规律，其结果与Bouzidi等[9]的试验结果吻合得很好，以此说明了所提出模型的合理性.随后，徐长节等[14]、Xu等[15]及Ding等[16]基于非局部-Biot理论研究了饱和土中深埋、浅埋圆形衬砌及浅埋复合式衬砌对入射P波的散射问题.结果表明，高频下孔隙尺寸对衬砌动应力影响显著，而低频情况下，非局部-Biot理论解与经典Biot理论解基本一致.Tong等[17]利用非局部-Biot理论，分析了非局部参数对饱和土中Rayleigh波的传播特性的影响，结果仍表明高频下孔隙尺寸对波传播特性的影响不可忽略.由以上分析可知，高频下，饱和土中孔隙尺寸及孔隙动应力会对波的传播特性产生较大的影响，为此，研究孔隙尺寸在平面波作用下对地表动力响应的影响显得尤为重要.

本文基于非局部-Biot理论，构建了P波及SV波入射下，饱和土地基地表响应计算模型，采用波函数展开法，得出了地表位移及水平应力的解析解，通过算例分析研究了非局部参数、入射波频率及入射角对地表位移及应力响应影响的变化规律.

1 计算模型

假设平面P1(SV)波以入射角为θα(θβ)经饱和土半空间传播至地表，如图1所示.饱和土地基为典型的两相介质，因此，入射波经地表反射将产生P1、P2及SV波.

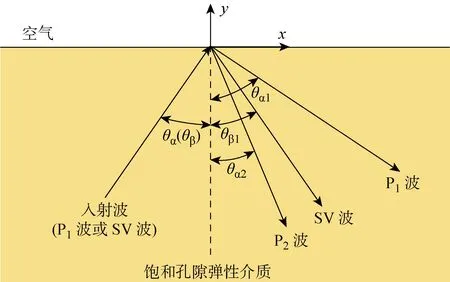
图1 计算模型Fig.1 Calculation model

P1波入射时：

(1)

SV波入射时：

(2)

式（1）中，fsr为转发器接收信号频率，fst表示卫星天线发射频率，即卫星下行频率，fs为卫星转发器本振频率。

2 非局部-Biot理论控制方程

饱和土中总波场由入射波场和散射波场构成，本文考虑入射波场分别为P波和SV波情况.

灯草老爹说：“瓦是盖在屋上的，本来就捂不得。”他看了一眼刁德恒，“当然当然，刚出窑的瓦例外，不能被雨淋了。但是出窑之后放一两天，热气没了，如果再盖就会破裂。这个道理，我本来想跟刁队长说，但他老拿手枪指着我，我就不敢多嘴……”

本构方程：

(3)

高中生物课堂教学质量水平的提高，要充分注重方法的科学应用，而生活化的教学方法的应用就显得比较重要，这是将学生生活中比较熟悉的情景内容在生物课堂中呈现的教学方法，能促使学生对生物知识的学习产生共鸣，从而激发学生学习的积极主动性。生活化教学方式的应用过程中要注重从多方面加强重视，将教学方法的应用要点进行把握，这样才能有效提高生物教学的质量。生活化教学方法的应用过程中，就要充分注重师生间的沟通交流，教师对学生要能够有所了解，这样才能更好地开展相应教学活动。生物课堂的生活化教学不能只注重学生的学习成绩，要注重学生课堂学习表现以及学习的过程表现。

运动方程：

(4)

SV波入射：

(5)

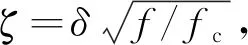
3 波场的求解

3.1 饱和土中散射波场的求解

β9=-ρfτ2ω2

(6)

将式(6)带入式(4)，并消去φf和Ψf，可得：

式中：ξ1、ξ2及ξ3为流体部分势函数与土骨架部分势函数的比值，其表达式为

(7)

实际工程中人们所关心的问题是地表的位移及应力变化，地表位移可采用式(15)中第1式计算，所得出的位移为与入射波幅值的比值(本文取入射波幅值为φ0=1)，因此后续分析中的位移为无量纲位移，针对P波和SV波入射分别采用ka1和kβ对其位移进行无量纲化.地表应力采用无量纲应力，即

参数关系为

β1=(λ+α2M+2μ-ρω2τ2)

β2=αM-ρfω2τ2

煨姜 煨姜为生姜经煨制的品名，生姜经煨制后辛温不燥，辛散药力不及生姜，温中止呕功效又较生姜好，适用于腹痛呕吐、大便泄泻等症。

β3=-ρω2,β4=-ρfω2

β5=αM,β6=M

β8=μ-ρτ2ω2

为求解式(4)，引入土骨架标量和矢量势函数φs和Ψs，及流体部分标量及矢量势函数φf和Ψf，根据Helmholtz分解定理，饱和土中位移场可表示为

其中：ω为圆角频率.

目前的技术水平已经可实现不受控制的核聚变，如氢弹等核武器早已登上历史舞台。但如要使核聚变释放出的巨大能量可有效为人类所利用，则必须对其进行人为控制，即受控核聚变。

由式(7)可知，饱和多孔介质中存在两种P波，土骨架部分的P波势函数可表示为

φs=φs1+φs2

(8)

同理，由式(4)和(6)可得流体部分P波和SV波势函数为

(9)

（三）在学习“健康的生活”一章内容时，教材中提到“拒绝毒品、远离毒品”。青少年时期是一个“出生牛犊不怕虎”的时期，对什么都感到好奇，对什么都想试一试，再加上对毒品的危害认识不清，致使受害人数较多。青少年时期正是迅速生长发育的时期，若吸毒危害比成年人更为严重，所以我们要在青少年中开展禁毒教育，使之充分认识毒品的危害，自觉抵制毒品、远离毒品。在每年的6月26日，制作相关内容的展板，宣传相关的禁毒知识，并开展讲座，以具体事例教育学生，真正从思想上树立高度警惕意识。

产业集聚过程中所产生的环境效应是经济因素、生态因素、社会化因素、文化因素、政治因素、地理因素等共同作用的结果，因此，通过多学科交叉研究产业集聚与环境效应相互作用机制是未来研究的趋势。将多因素纳入系统的研究框架，考虑

ξ3=-β4/β7

1）对一些已经废弃但是确实可以体现城市历史文化特色的街道名称进行调研，必要时予以恢复。潍坊市2018年发布的《关于道路命名征求意见的公告》中将原来已经废弃的“状元胡同”重新启用，改为“状元街”。

3.2 饱和土中总波场

根据文献[13]可知，饱和孔隙弹性介质的非局部-Biot理论的运动方程为

国家应加大金融市场的建设，鼓励机构投资者和中小投资者参与。同时，营造良好的市场环境，提供信誉担保，预防不诚信行为的发生，促进我国资产证券化市场的发展。

当下对中国建筑的考古挖掘和文献整理已取得一定成就，这让我们有机会去触碰中国传统建筑形式背后的文化渊源，回归中国传统建筑的原初形式的探讨，文章透过史料去探究和诠释中国古建山面入口到檐面入口面向转变的内在逻辑，这种入口面向转变是由建筑技术、居住经验、礼制文化等共同作用、逐渐演变的结果，并且通过对其探究，让我们可以理解一些建筑形式的时空联系和文化内涵。探讨传统建筑的形式逻辑这类问题将有利于我们摆脱对传统形式拙劣的模仿，做出有中国性的设计。

入射波为P波时：

(10)

入射波为SV波时：

(11)

此处需要说明的是，入射波为SV波时，由于P1波波速通常大于SV波波速，当SV波的入射角达到临界角θcr1时，P1波的反射角将大于90°，此时，P1波表现出随深度增加，其幅值呈指数减小的非均匀波.与此同时，在软黏土介质中，P2波波速也有可能大于SV波波速，此时将存在第二个临界角θcr2.由波的反射关系，可得两个临界角为

(12)

为便于分析，将式(2)表示为

(13)

式中：K1、K2及K3为反射波待定系数，

k=kβsinθβ=kα1sinθα1=kα2sinθα2

为提高公路沥青路面运行使用的整体性与安全性，路面表面的施工应进行防水施工处理，以降低雨水环境对其结构稳定性带来的负面影响。此外，相关人员还应在公路工程的两侧设置排水沟，以使雨水能够快速排除，进而降低对路面结构作用效果带来的影响。

4 边界条件及待定系数求解

4.1 应力位移与势函数关系

由式(3)可知，非局部-Biot应力张量与经典Biot理论应力张量满足

即

(14)

结合式(3)、(6)及(14)，应力、位移与势函数关系可表示为

(15)

式中：ux、uy分别为x、y方向土骨架位移；wx、wy分别为x、y方向流体相对土骨架位移；σxx、σyy、σxy分别为x、y方向正应力与切应力；Pf为孔隙水压力.

4.2 边界条件

考虑到地表零应力及透水特性，可将其边界条件表示为

(16)

将式(1)和(13)分别代入式(15)，并结合式(16)可求出P波及SV波入射下势函数的待定系数，待定系数求解方程组如下[3].

P波入射：

(17)

式中：ρ为土体密度；ρf为流体密度；m=ρf/n0，b=ηF(ξ)/k，η为流体黏滞系数，k为流体渗透系数；F(ξ)为高频下黏性修正系数，其表达式为[18]

(18)

系数矩阵表达式见表1.

通过式(17)，并结合表1即可求出反射系数，从而可利用式(15)求解出饱和土中位移及应力表达式.

表1 系数矩阵表达式Tab.1 Expression of coefficient matrix

5 结果与讨论

式中：kb为剪切波波数，满足

加特可（广州）自动变速器有限公司是加特可株式会社在海外独资设立的第二家生产基地。公司于2007年4月在以高新技术为主导的广州经济技术开发区科学城成立，注册资金7 500万美元，主要生产无级自动变速器（CVT）。公司在2012年4月成立了“加特可中国品质技术中心”，该中心集顾客品质保证、SQA、开发和采购等功能于一体，形成以组织形式对市场品质、车辆适用开发和零部件国产化作出高效反应的机制。

(19)

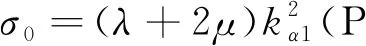
5.1 结果验证

为验证本文结果的合理性，将本文计算结果与Lin[3]结果进行对比(见图2)，为此，取流体黏滞系数η=0，P波及SV波入射下，同样水平位移(Ux)及竖向位移(Uy)分别采用kα1和kβ进行无量纲化，其余参数见文献[3].由图2可知，P波及SV波入射下，本文水平及竖向位移计算结果与文献[3]结果一致，由此说明本文计算结果的正确性.

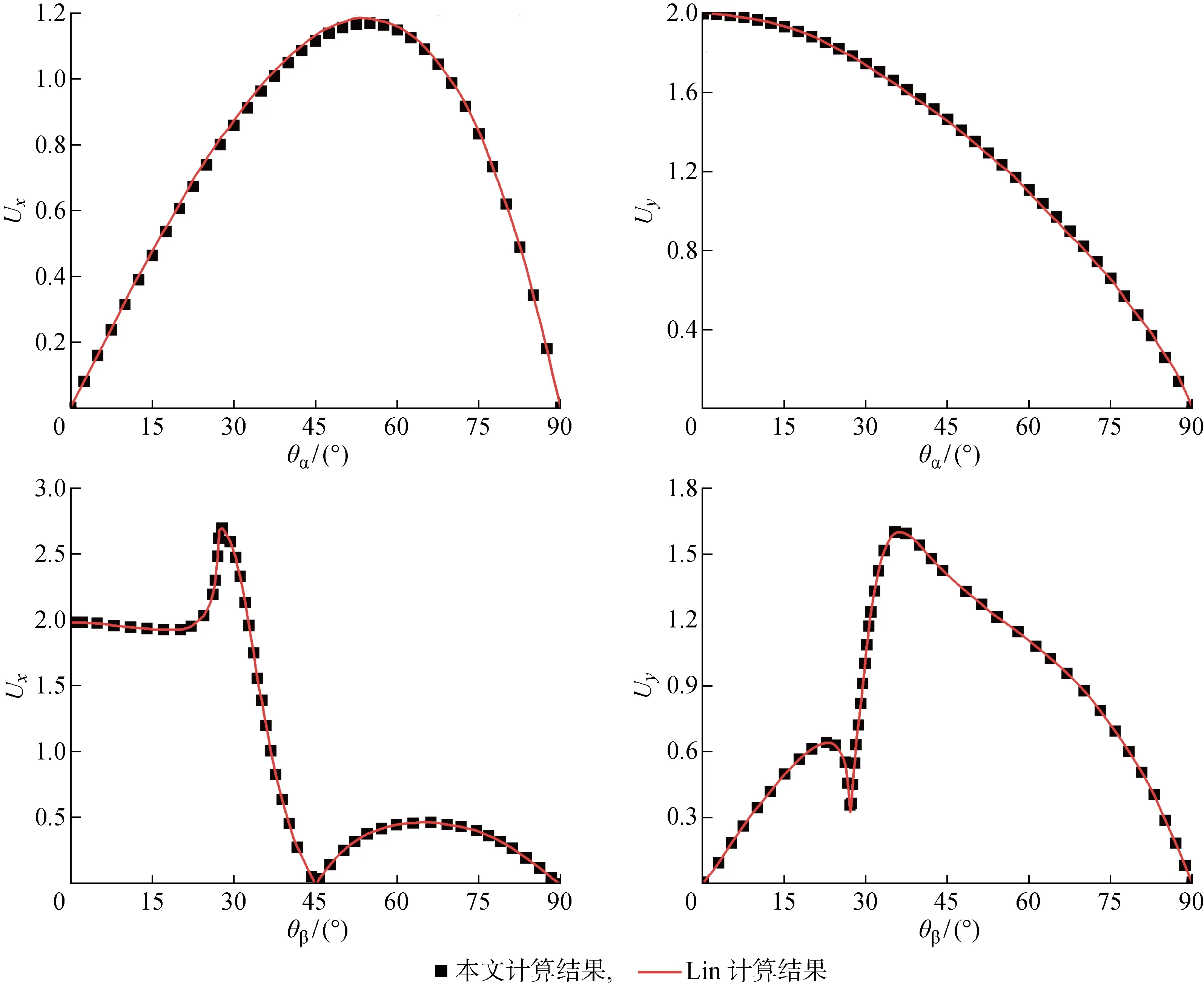
图2 本文结果与文献[3]结果对比曲线Fig.2 Comparison of results obtained in this paper with those in Ref.[3]

5.2 算例分析

为充分分析P波及SV波作用下饱和地基地表动力响应情况，本文选取饱和土体计算参数，见表2所示.

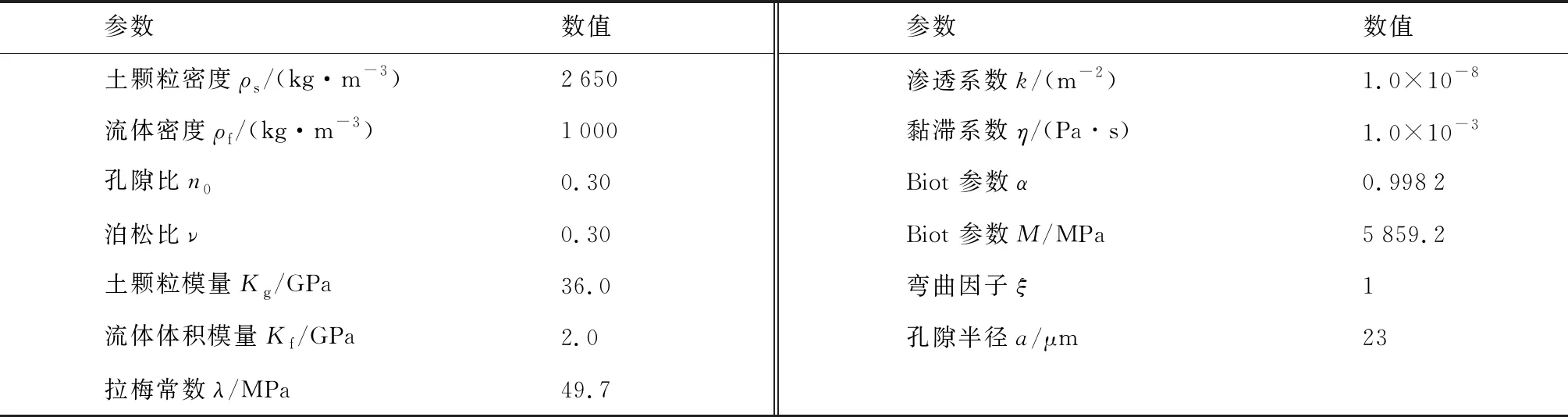
表2 饱和土体物理力学参数Tab.2 Physical and mechanics parameters of saturated soil

图3、4分别为P波及SV波作用下，地表位移及应力随非局部参数的变化曲线(入射角为30°).由图可知，当入射频率f=10 Hz时， 地表位移及应力随非局部参数的增加几乎没有变化，而随着入射波频率的增加，非局部参数对地表位移及应力具有显著的影响.如当入射波频率达到 1 000 Hz，P波入射情况下，地表位移随非局部参数出现增加而增大，应力随非局部参数增加而呈现出减小的趋势.SV波入射情况下，地表水平位移及水平应力均随非局部参数的增加而减小，其竖向位移随非局部参数的增加而增大.其原因是非局部参数的增加，意味着饱和土中孔隙尺寸的增大，入射频率较低(如10 Hz)时，波长远大于孔隙尺寸，此时孔隙尺寸对波传播的影响可以忽略，而随着入射波频率(如 1 000 Hz)的增加，饱和土中波长减小，此时随着孔隙尺寸的增加，波长与孔隙尺寸更加接近，导致孔隙尺寸对波传播特性产生较大的影响.此外，从图3和4中还可以看出，随着入射波频率的增加，地表水平位移及竖向位移的起始值逐渐增大，这是由于入射波频率增加引起地表位移增大，而入射波频率对地表应力起始值影响不大.

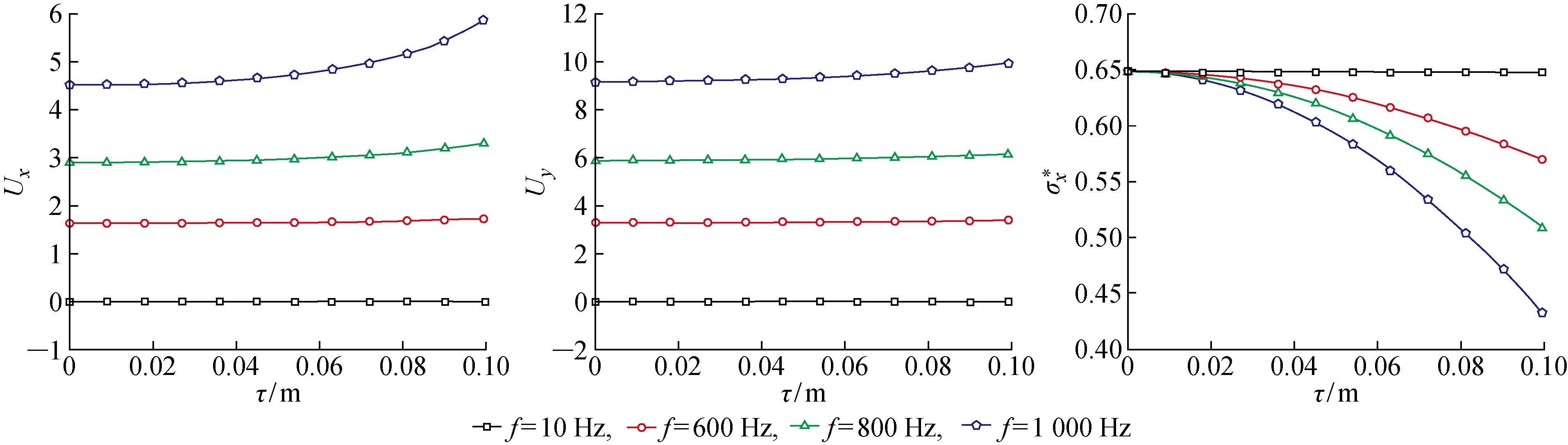
图3 P波入射下地表位移及应力随非局部参数的变化Fig.3 Displacement and stress of ground surface versus nonlocal parameter subjected to P wave

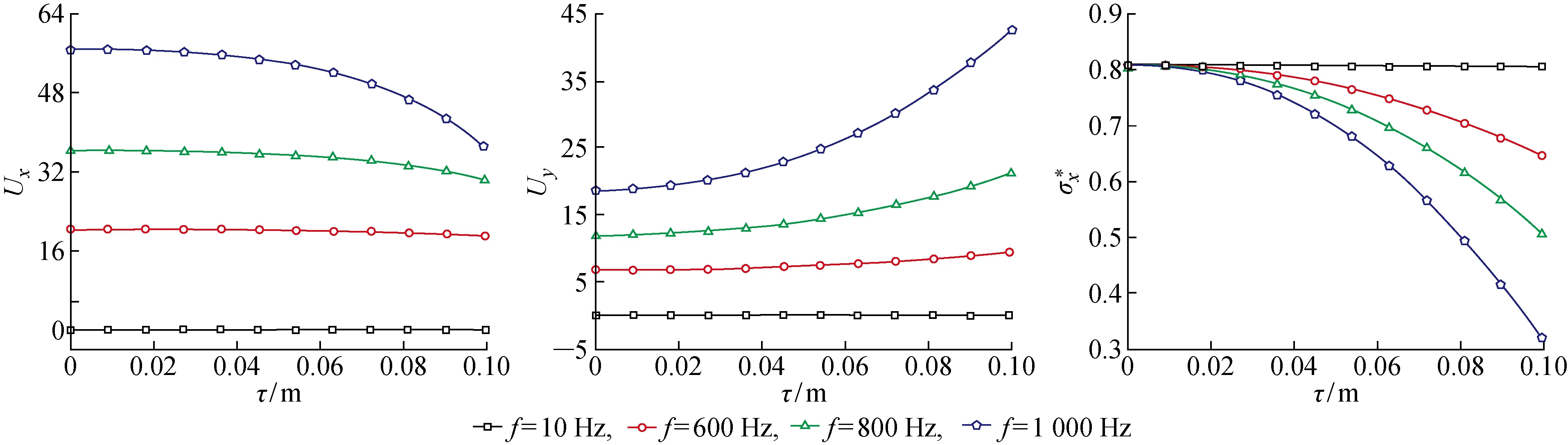
图4 SV波入射下地表位移及应力随非局部参数变化Fig.4 Displacement and stress of ground surface versus nonlocal parameter subjected to SV wave

图5、6分别为不同非局部参数时，P波及SV波入射下，地表位移及应力随入射波频率变化曲线，其中P波及SV波入射角均为30°.由图可知，当入射波频率较低时，本文理论计算结果与经典Biot理论计算结果(τ=0.00 m)基本一致，而随着入射波频率的增加，本文理论计算结果与Biot理论计算结果逐渐显现出差异.由此说明，高频下孔隙尺寸对波传播特性的影响不可忽略.倘若以与经典Biot理论偏差达5%为分界点，由图可以看出，频率分界点(与Biot理论偏差达到5%的频率点)随非局部参数的增大而减小.如SV波入射下，地表水平位移在非局部参数为0.06、0.08及0.10 m时，所对应的临界频率分别为892、672及538 Hz，其原因是非局部参数越大，其对应的饱和土孔隙越大，从而导致其对波传播特性的影响越大.

图5 P波入射下地表位移及应力随入射频率变化Fig.5 Displacement and stress of ground surface versus input frequency subjected to P wave

图6 SV波入射下地表位移及应力随入射频率变化Fig.6 Displacement and stress of ground surface versus input frequency subjected to SV wave

图7、8分别为P波及SV波作用下，地表应力及位移随入射波入射角度的变化曲线，入射频率为1 000 Hz.由图可知，P波入射下，地表水平及竖向位移随非局部参数的增加而增大，而应力随非局部参数的增大而减小.SV波入射时，地表水平位移及应力在入射角为45° 时减小为0，这是由于SV波在45° 入射时， 在地表发生全反射，此结论与经典弹性解相同[19].在45° 之前水平位移随非局部参数增加呈现出增加的趋势，在此之后随非局部参数的增加而呈现出减小趋势.地表竖向位移随非局部参数增加而增大.此外，图中虚线内出现的拐点随非局部参数增大而向左移动，这是由于非局部参数增加使得临界角度减小所致.对比图7、8可知，对于相同幅值的P波、SV波作用下，SV波所引起的地表响应大于P波.

为了研究生物炭添加量对土壤水分保水性能的影响，采用每天称重的方法测得土壤每天的水分蒸发量，计算土壤水分总蒸发量，同时还对陈化2天后及自然状态下蒸发12天的土壤含水量进行了计算，结果如图6和图7所示。由图6可以看出，土壤水分日蒸发量出现上下波动现象，整体服从相似的规律。由图7可以看出，样品陈化2天后的含水量随生物炭添加量的增加而增大，水分总蒸发量亦表现出相似的趋势，但每个样品蒸发总量相差不大，土壤最终含水量随生物炭含量的增加而增大，即生物炭添加量越大，虽然蒸发量大，但由于土样吸水量大，因此最终含水量还是最高。

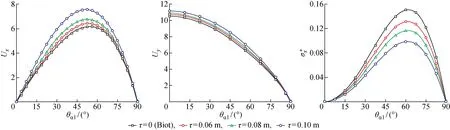
图7 P波入射下地表位移及应力随入射角变化曲线Fig.7 Displacement and stress of ground surface versus incident angle subjected to P wave

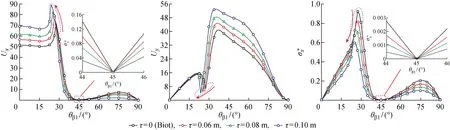
图8 SV波入射下地表位移及应力随入射角变化Fig.8 Displacement and stress of ground surface versus incident angle subjected to SV wave

6 结论

基于非局部-Biot理论，利用波函数展开法，求解了P波和SV波作用下，饱和土地基地表响应问题的解析解.将本文解退化为经典Biot理论下无黏性解，并与文献[3]对比，结果一致.通过算例分析研究了非局部参数、入射波频率及入射角对地表动力响应的影响，得出如下结论：

(1) 非局部参数对地表动力响应的影响与入射波频率有关，入射波频率较低(10 Hz)时，本文解与经典Biot理论解基本一致，随入射波频率增加(如 1 000 Hz)，非局部参数对地表影响的影响较为显著.其原因是频率越高，波长越小，孔隙尺寸对波传播特性的影响越大.

(2) 入射波频率对地表响应的影响与非局部参数有关，倘若以与经典Biot偏差5%为分界点，可知非局部参数越大，频率分界点越小.

(3) P波入射时，地表位移随非局部参数的增大而增大，应力随非局部参数的增大而减小.SV波入射时，地表水平位移及应力在入射角为45° 时，其值为0，这是由于SV波在45° 时发生全反射所致.此外，非局部参数通过减小SV波入射的临界角，而使地表响应的拐点向左移动.相同幅值的P波和SV波作用下，SV波所引起的地表响应大于P波.

本文理论及研究成果可为半空间饱和土中波动问题的研究提供借鉴.