Pasternak地基降水对邻近管线影响的解析研究

徐长节，曾怡婷，田 威，陈 明

(1. 浙江大学 滨海和城市岩土工程研究中心， 杭州 310058； 2. 华东交通大学 土木建筑 学院， 南昌 330013； 3. 杭州市水务控股集团有限公司， 杭州 310009； 4. 浙江省交通投资集团有限公司， 杭州 310000)

随着城市地下空间开发利用规模的不断扩大，地下工程邻近既有地下管线的情况越来越常见[1-3].基坑开挖前往往需要展开抽水试验及试泵试井等预降水工作来获取水文地质参数，确保降水井在开挖施工时能达到施工降水设计要求，这会引起周边土体及结构物的沉降变形.地下管线作为城市生命线，一旦发生事故会造成巨大的经济损失.因此，深基坑开挖前预降水引起邻近既有地下管线的挠曲不可忽略，准确预估变形量及分析结构受力薄弱点对地下管线的变形控制及防护至关重要.

目前，对于基坑降水引起的土体沉降及管线变形问题国内外已有较多研究.Shen等[4-7]等对不同截降水条件下水位的分布进行了现场试验、数值模拟及解析预测.Zhang等[8]对深层承压含水层多井抽水回灌试验进行数值模拟，分析了地下水和地层对抽水回灌的影响.Zeng等[9-10]指出基坑开挖前预降水引起的挡墙及周边土体变形可达厘米级.黄戡等[11]基于流固耦合理论建立三维仿真模型，分析渗流特性、基坑开挖过程、不同降水速度下基坑施工特性以及其对邻近地铁的影响.郑刚等[12]进行了承压层减压降水对既有盾构隧道影响的有限元模拟，分析了既有隧道相对于承压含水层不同位置时的横断面内力、变形及周围土体应力场.施成华等[13]推导了基坑降水漏斗曲线方程及考虑水的渗流作用的基坑周边土体有效应力的计算公式, 并由此导出了考虑渗流作用的基坑降水地表沉降计算公式.周念清等[14]采用三维有限差分法对基坑降水进行模拟，同时对基坑降水引起的地面沉降进行计算. Wang等[15]对某地铁基坑降水井-隔水帷幕相互作用下的地面沉降进行了数值模拟.上述研究大多集中于基坑施工阶段的开挖及降水影响，而开挖前阶段的降水对管线的影响研究却少有涉及，管线在降水作用下的空间变形响应研究则不多见.

目前理论解析方法求解管线变形常采用弹性地基梁模型.传统的Winkler地基模型假设土体表面任意一点的应力与该点的位移成正比而与其他点的应力状态无关，忽略了地基变形的连续性，许多学者在此基础上提出了改良的“双参数模型”[16].Tanahashi等[17-18]提出了基于Pasternak地基模型的二维弹性地基梁变形及受力解析计算方法.Liang等[19]通过引入Pasternak模型提出了一种简化的分析方法来预测与邻近开挖有关的盾构隧道行为.可文海等[20]运用修正Vlasov模型中的迭代流程计算出Pasternak模型的关键参数(弹性系数与剪切系数).Zhang等[21]基于Pasternak地基模型，研究了基坑降水及开挖对其下卧既有隧道的影响，然而其研究过程中未考虑降水引起管线附加荷载的空间变化.

本文针对砂土地基，采用二阶段分析法，基于Pasternak弹性地基梁理论，考虑土体剪切作用，结合土的有效应力原理和Dupuit假设，考虑降水引起地基附加应力的空间变异性，推导了由单井降水引起的邻近管线附加荷载，并进一步推导管线变形解析解.通过算例分析，研究了不同参数下管线的整体变形及受力规律，可为相关工程的管线防护提供参考.

1 基于Pasternak弹性地基梁理论的管线变形推导

如图1所示，管线距降水井距离为d，将对称点O视为管线中心和坐标轴原点，沿管线建立x轴，x=l处距降水井距离为r，降水影响半径为R，D、D′为影响半径与管线交点.图2为相应的xOz平面内的Pasternak弹性地基梁模型，z方向为竖直向下，σ(l)为x=l处由降水引起的附加荷载.为计算降水导致的管线变形，本文基于以下假定和简化处理：

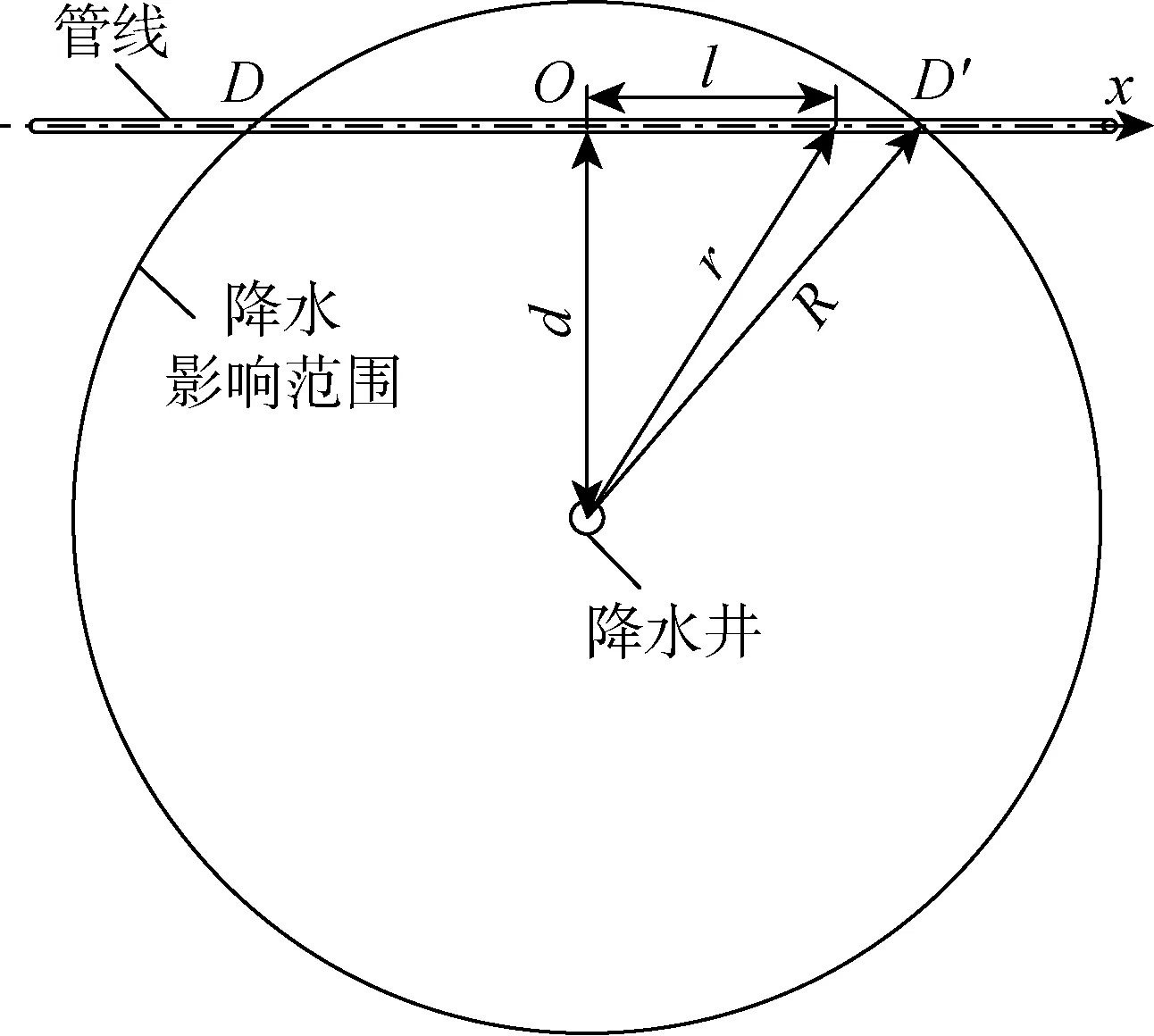
图1 管线及降水井平面位置Fig.1 Plane position of pipeline and dewatering well

图2 计算模型Fig.2 Calculation model

(1) 将地下管线视为无限长的Euler-Bernoulli梁；

(2) 将地基土视为可考虑剪切刚度的Pasternak弹性地基；

(3) 土层为无限潜水各向同性均质含水砂土层；

(4) 存在影响范围为R的补给边界，边界外水头不变；

(5) 忽略管线直径对降水的影响；

(6) 只考虑xOz平面内管线的受力和变形.

1.1 降水曲线公式

如图3所示，初始水头为H的无限潜水含水层中有一口半径为r0的完整井，井管处设计降水水位为h0，经长时间定流量抽水后形成相对稳定的降水漏斗[22]，距离降水井r处水头为h.基于Dupuit假定，等水头面为共轴圆柱面，不同过水断面流量与井的流量Q相等，为

图3 潜水完整井降水曲线Fig.3 Drawdown curve during phreatic well dewatering

(1)

式中：k为渗透系数.

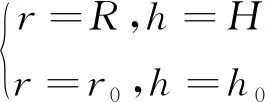
(2)

(h0≤h≤H,r0≤r≤R)

1.2 降水引起的有效应力增加

土体的强度和变形主要由有效应力决定，降水前后有效应力变化可根据降水后水位线与计算点相对位置分为两种情况，如图4所示.图中计算点A、B埋深与初始水位的高差分别为hA、hB，降水后水位线位于A下方、B上方，埋深为h1.

图4 降水前后有效应力计算示意图Fig.4 Schematic diagram of effective stress calculation before and after dewatering

A点有效应力计算：

降水前，

(3)

降水后，

(4)

所以A点降水前后有效应力变化值为

(5)

B点有效应力计算：

降水前，

(6)

降水后，

(7)

所以B点降水前后有效应力变化值为

Δh(γ+γw-γs)

(8)

1.3 降水引起管线附加荷载

如图5所示，附加荷载计算分为两种情况，一种为降水前后水位始终位于管线上方，另一种为降水后部分水位降到管线下方，对应的附加荷载分布形式如图6所示.

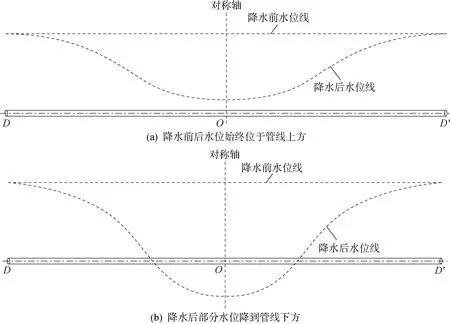
图5 降水前后水位线沿管线长度分布Fig.5 Water level distribution along pipeline length before and after dewatering

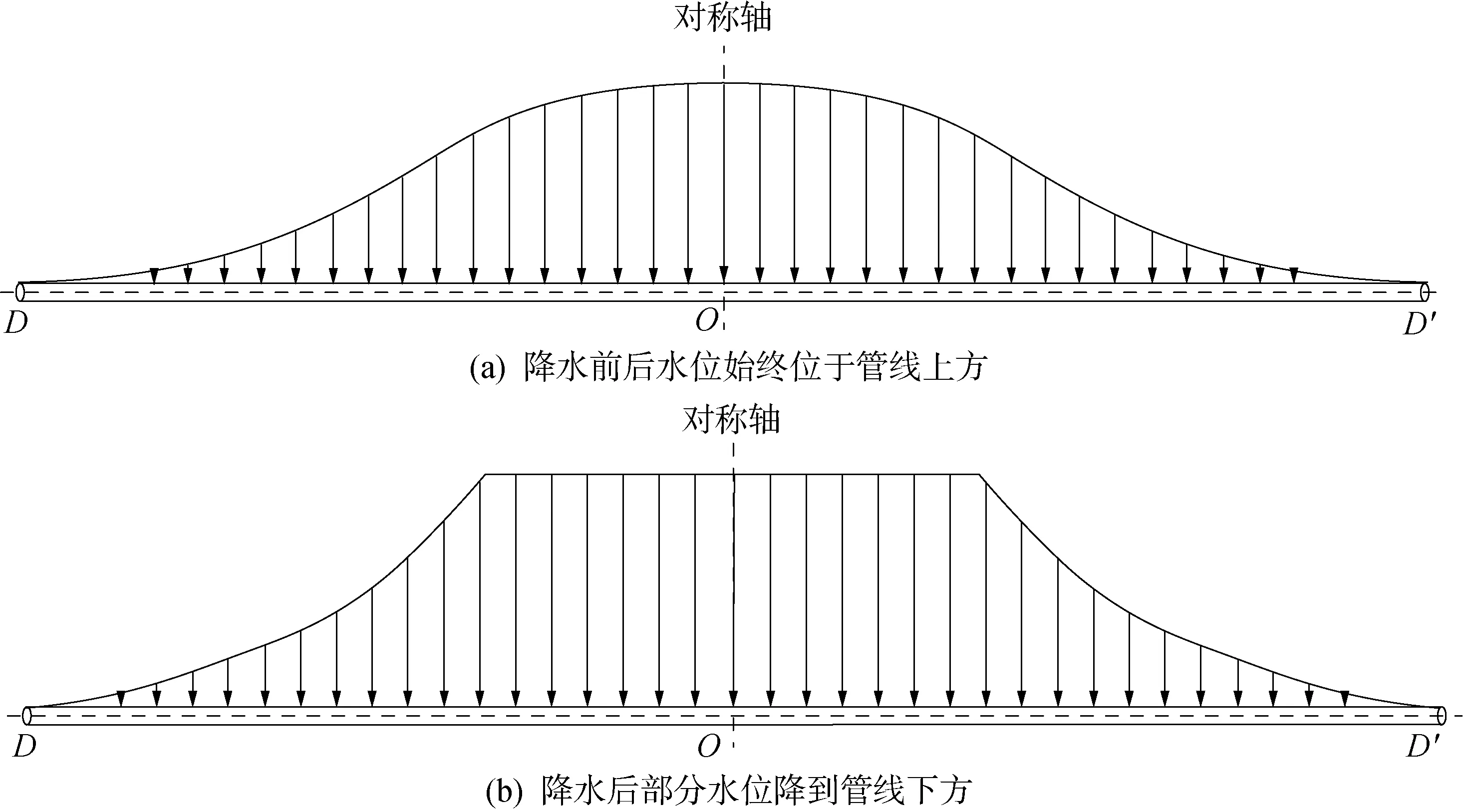
图6 降水后附加荷载沿管线分布Fig.6 Additional load distribution along pipeline after dewatering

(1) 降水前后水位始终位于管线上方.如图1所示，管线上任一点x=l处与降水井距离为

(9)

则由式(8)得管线沿长度受力为

σ=Δσ′=(H-h)(γ+γw-γs)

(10)

将式(2)代入式(10)得

(γ+γw-γs)

(11)

将式(9)代入式(11)得

(γ+γw-γs)

(12)

(2) 降水后部分水位降到管线下方.管线受力分为两部分，降水后水位位于管线上方部分受力为式(12)，由式(5)得降水后水位降到管线以下部分受力为定值：

σ=Δσ′=hA(γ+γw-γs)

(13)

当hA=H-h时，为分界点， 即

(14)

解得

(15)

综上，降水引起管线附加荷载分布为

σ(l)=

(16)

1.4 基于Pasternak 地基模型的管线位移推导

Pasternak 地基模型地基反力和位移的关系式为[18]

(17)

式中：p为地基反力；K为地基反力系数；w为地基位移；Gp为地基切变模量.

(18)

地基反力系数K及地基切变模量Gp可按以下式取值[17，19]：

式中：vs和Es分别为土体的泊松比和弹性模量；Ht为土体剪切层厚度，取为管线直径的2.5倍[19].

根据Euler-Bernoulli 梁理论，降水引起管线位移的控制方程为

(21)

式中：E为地下管线弹性模量；I为地下管线横截面惯性矩；q为管线受力；b为管线直径；σz(x)为降水引起的管线附加荷载.把式(17)代入式(21)整理得

bσz(x)

(22)

该式对应的齐次方程为

(23)

特征方程为

(24)

式中：λ为特征方程的特征根.

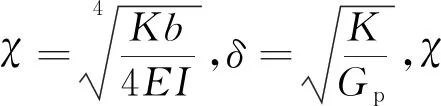
(25)

所以有

(26)

特征方程有两个单重复数根，解得：

(27)

(28)

(29)

故得式(27)的通解为

w(x)=eαx(c1cosβx+c2sinβx)+

e-αx(c3cosβx+c4sinβx)

(30)

式中：c1,c2,c3,c4为4个积分常数，由于附加荷载σz(x)关于原点对称分布，所以取x≥0进行分析求解.σz(x)不是均布力，故先求集中应力P作用下管线挠度，并利用坐标变换求得任一点在集中应力作用下的管线挠度，再通过积分求得在σz(x)作用下的管线挠度.

如图7所示，假设x=0处作用集中应力P，当x→∞时，w(x)=0，代入式(30)可得c1=c2=0，又因为此时式(22)的一个特解为w*=0，所以σz(x)为集中应力P时式(22)的通解为

图7 集中力作用下的管线与Pasternak地基模型Fig.7 Pipeline on Pasternak foundation model at concentrated load

w(x)=e-αx(c3cosβx+c4sinβx)

(31)

(32)

将式(31)代入(32)解得：

(33)

将式(33)代入式(31)得x=0处作用集中应力P下的挠度方程为

(34)

利用坐标变换求得任一点x=l处在集中应力σz(l)dl作用下引起的管线挠度为

(35)

积分得管线挠度方程为

(36)

式中：l1、l2为附加荷载作用范围，分别为

(37)

2 算例验证

为验证本文解析方法，将计算结果与抽水试验下邻近管线监测结果进行对照，并与PLAXIS三维有限元数值模型计算结果进行对比分析.

试验场地含水层厚度在20.0～26.4 m，初始水位埋深在1.3～2 m，含水层主要由砂土和粉砂土层构成，下部淤泥质粉质黏土和粉质黏土构成了潜水含水层的隔水底板，具体参数详见表1.抽水试验为混合稳定流抽水试验，即将浅部粉及砂性土作为一个整体的均质含水层考虑(无限边界)，并将抽水井模拟为淹没滤水管井壁进水的完整井.

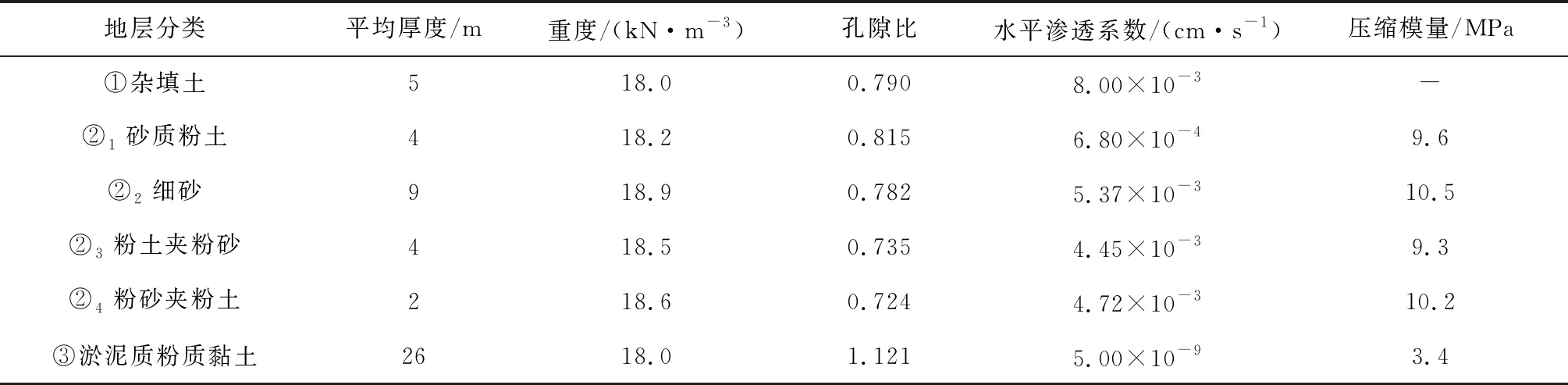
表1 试验区地层参数Tab.1 Soil parameters of test area

试验采用单孔抽水试验方法，共计1个落程，在距现有管线10 m处设置一口试验井，抽水井降深sw随时间t的变化如图8所示，降深值在较短时间内趋于稳定，稳定后抽水量为28.30 m3/h，降水深度为12 m.

图8 抽水试验s-t图Fig.8 s-t curves of pumping test

如表2所示，为对比数值模拟和解析计算结果，数值模型及解析计算地层参数取用试验土层参数加权平均的近似值，综合渗透系数取抽水试验实测值.管线参数如表3所示，管线采用梁单元进行模拟，地基土体采用线弹性模型.图9为数值计算模型，模型平面取边长为500 m的正方形，该距离超过影响半径范围，模型深度取60 m，为降水深度的5倍，模型

图9 数值计算模型Fig.9 Numerical calculation model

表2 数值模拟参数Tab.2 Parameters of numerical simulation

表3 管线计算参数Tab.3 Parameters of pipeline calculation

中心设置排水线模拟降水井抽水，管线位于距降水井10 m处，模拟抽水工况时将排水线处水头孔压设置为-12 m，数值模型四周边界和地表设为地下水渗流的补水边界，模型底部为关闭地下水渗流的隔水边界，图10所示为模拟降水后管线竖向变形示意图.

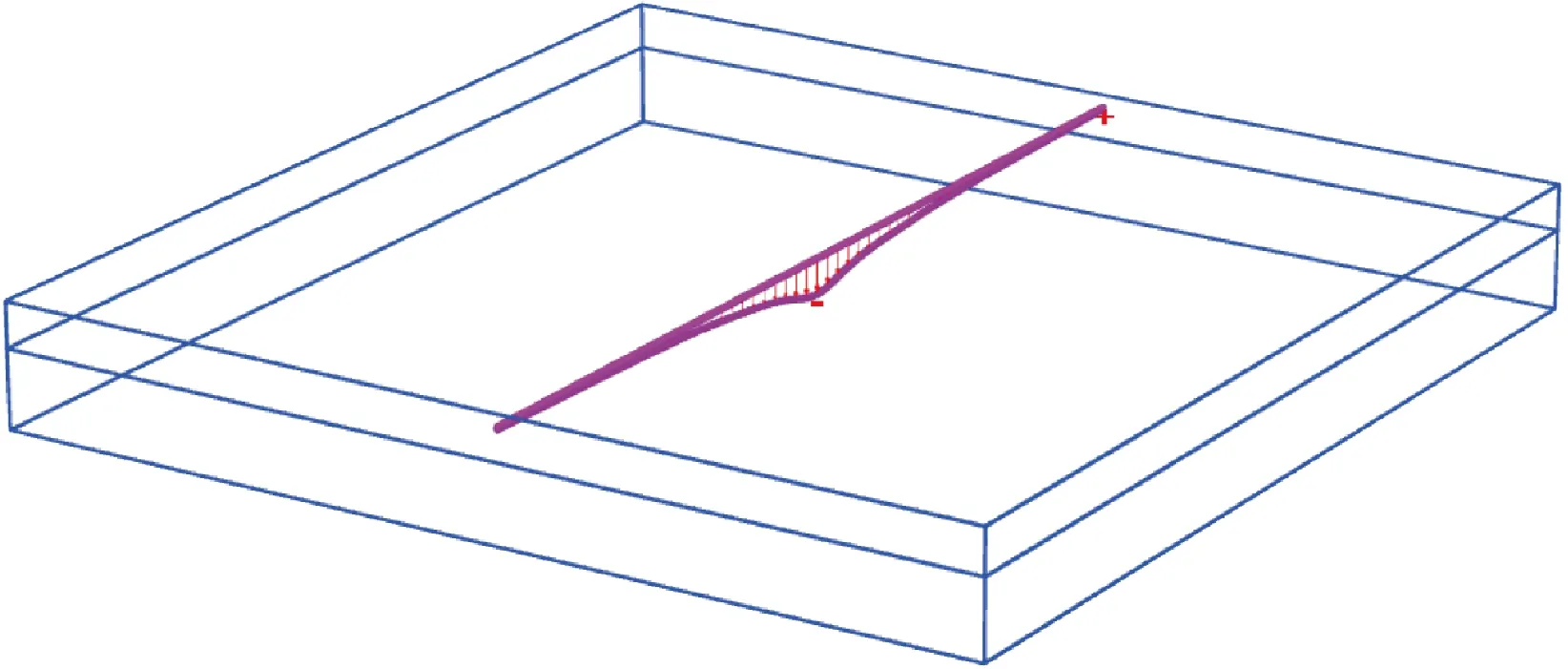
图10 降水后管线竖向变形示意图Fig.10 Schematic diagram of vertical deformation of pipeline after dewatering

用MATLAB对式(36)进行编程计算，抽水试验、数值计算以及本文解析解得到的管线变形如图11所示，x=0处为管线距降水井最近处.可见，三个结果在±100 m范围内吻合较好，从而验证了本文解析解的合理性.位移沿管线长度呈中间大两头小的类似于正态分布的对称非线性分布，x=0处存在最大位移值约9 mm，可见降水引起邻近管线位移可达厘米级，在工程中预降水带来的影响不可忽略[23].x=0处实测变形比解析解小9%，由于Dupuit公式推导水位线时无法考虑潜水井存在渗出面，导致实际浸润曲线高于计算曲线，这种误差会随着管线上计算点与降水井距离的增大而减小.超出±100 m范围处理论计算结果偏小，主要原因在于有限元模型中没有降水影响半径，而理论模型中假定了一个降水影响半径R=234 m.理论与有限元计算位移误差小于1 mm，在合理范围内.

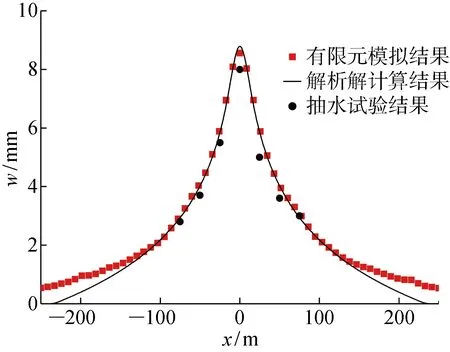
图11 解析解计算结果与数值模拟及抽水试验结果对比Fig.11 Result comparison of analytical calculation, numerical simulation, and pumping test

3 参数分析

变形计算公式w(x)是与所受附加荷载σz(l)及地基反力系数K、参数χ及ρ有关的函数，参数χ、ρ由土体及管线刚度决定，沿管线的附加荷载σz(l)则与降深、影响半径及管线与降水井间距等参数有关.为了研究管线在单井抽水下的受力变形规律，对这些参数进行了算例分析.

3.1 土体剪切刚度对管线受力变形的影响

以表2、3的参数为基础，保持其他参数不变，取ρ不同值：0，0.3，0.6，0.9，代入公式得到管线竖向位移w和弯矩M沿管线的分布，如图12、13所示.当ρ=0时，剪切刚度为0，Pasternak 弹性地基模型退化为传统的Winkler地基模型.ρ越大，对应的土体剪切刚度越大.此外，随着ρ增大，管线位移和弯矩都逐渐减小，其中ρ=0时的位移最大值与图11所示抽水试验所得管线最大位移值相差10%，误差为ρ=0.9时的两倍.当ρ从0变化到0.9时，弯矩最大值减小27%，说明在分析管线受力时不考虑土体剪切刚度将会引起较大误差.比起传统的Winkler 地基模型，Pasternak 地基模型考虑了土体在垂直方向上的实际剪切效应，管线刚度相对较小，采用Pasternak地基模型能更好地反映管线的受力及变形[16].

图12 不同ρ下的管线位移Fig.12 Deformations of pipeline at different ρ values

图13 不同ρ下的管线弯矩Fig.13 Bending moments of pipeline at different ρ values

3.2 降水井降水深度sw对管线受力变形的影响

为研究降水深度sw对管线受力变形的影响，在算例计算中分别取降水井降水深度sw为 4、8、12、16及20 m，得到管线竖向位移w和弯矩M沿管线的分布，如图14、15所示.

图14 不同降水井降水深度下的管线位移Fig.14 Deformations of pipeline at different drawdown of dewatering well

由图14可看出，随着sw的增大，管线最大位移从3 mm逐渐增大到11 mm，增大速率逐级减缓，管线发生位移的范围逐渐变大，从±80 m范围等距离发展到±400 m范围，这是由于计算时影响半径取值随sw增大而线性增大，管线所受附加荷载范围也随之变广.管线变形值超过最大值50%的部分集中在影响半径值25%范围内，超出该范围的管线变形较小，因此工程中应对影响半径25%范围内的管线变形进行重点监测及保护.

由图15可看出，管线受力主要在±50 m范围内，在这个范围外弯矩较小可忽略.sw从4 m增大到12 m的过程中，弯矩最大值出现在管线中心且逐渐增大.但sw从12 m增大到20 m的过程中，弯矩最大值开始减小，最大弯矩位置由中心向外偏移，出现两个弯矩峰值，sw为16 m、20 m时的峰值分别位于±6 m、±13 m，水位线与管线相交点也分别为±6 m、±13 m位置.可见，峰值出现在水位线与管线相交点附近，降水时应对该位置进行重点保护，相交点位置可由前文式(15)计算得到或者在工程监测中得到.由于随着sw增大，管线受到附加荷载增大，所以弯矩逐渐增大.但是当sw增大到一定值时，管线中间位置水位降到管线下方，如图5(b)所示，该部分附加荷载将不随sw增大而改变，而是为一定值σ=hA(γ+γw-γs)，其仅与降水前水头及管线埋深有关，相当于原弯矩叠加了降到管线以下水位引起的附加荷载所导致的负弯矩，因此弯矩最大值反而减小并由管线中心向外偏移.

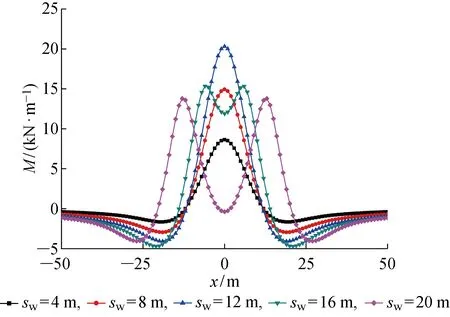
图15 不同降水井降水深度下的管线弯矩Fig.15 Bending moments of pipeline at different drawdowns of dewatering well

可见，存在最不利降深使得管线中心弯矩最大，该降深为管线与降水曲面相切时的临界降深，可由式(15)中l=0计算得到此时的降水井临界降深为

(38)

当sw超过临界降深后，管线最大弯矩将减小，且由管线中心向外偏移，出现两个弯矩峰值，峰值位于水位线与管线相交点附近.

3.3 降水井距管线距离d对管线受力变形的影响

为研究降水井距管线距离d对管线受力变形的影响，保持其他参数与前文一致，降水深度sw固定为12 m，管线埋深z为4 m和6 m时，分别取距离d为5、10、15及20 m进行算例分析.

如图16(a)和图17(a)所示，管线埋深z=6 m时，当d从5 m增大到10 m时，位移最大值减小15.8%，弯矩最大值减小46.3%.可见，d对管线变形有显著影响，d越大，管线变形越小，弯矩越小，因此在工程中降水点应尽可能远离管线.如图16(b)和图17(b)所示，管线埋深z=4 m时，d较小时，管线变形随d增大变化不明显，d增大到一定值后，管线变形才出现减小的趋势.弯矩有两个峰值，对称分布在管线两侧， 随d增大逐渐减小且向中心靠拢并回归为一个峰值.

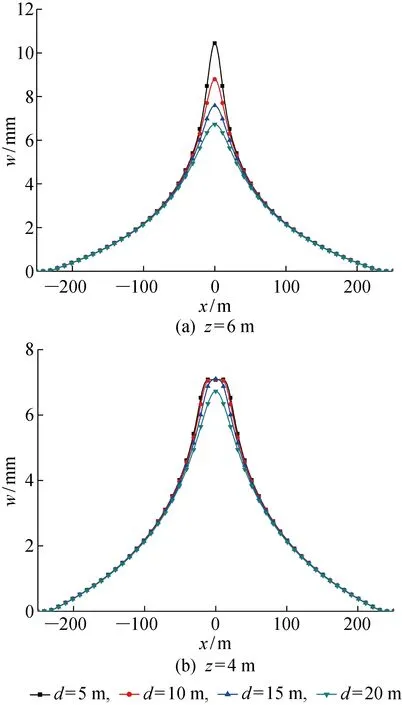
图16 降水井距管线不同距离时的管线位移Fig.16 Deformations of pipeline at different distance from dewatering well

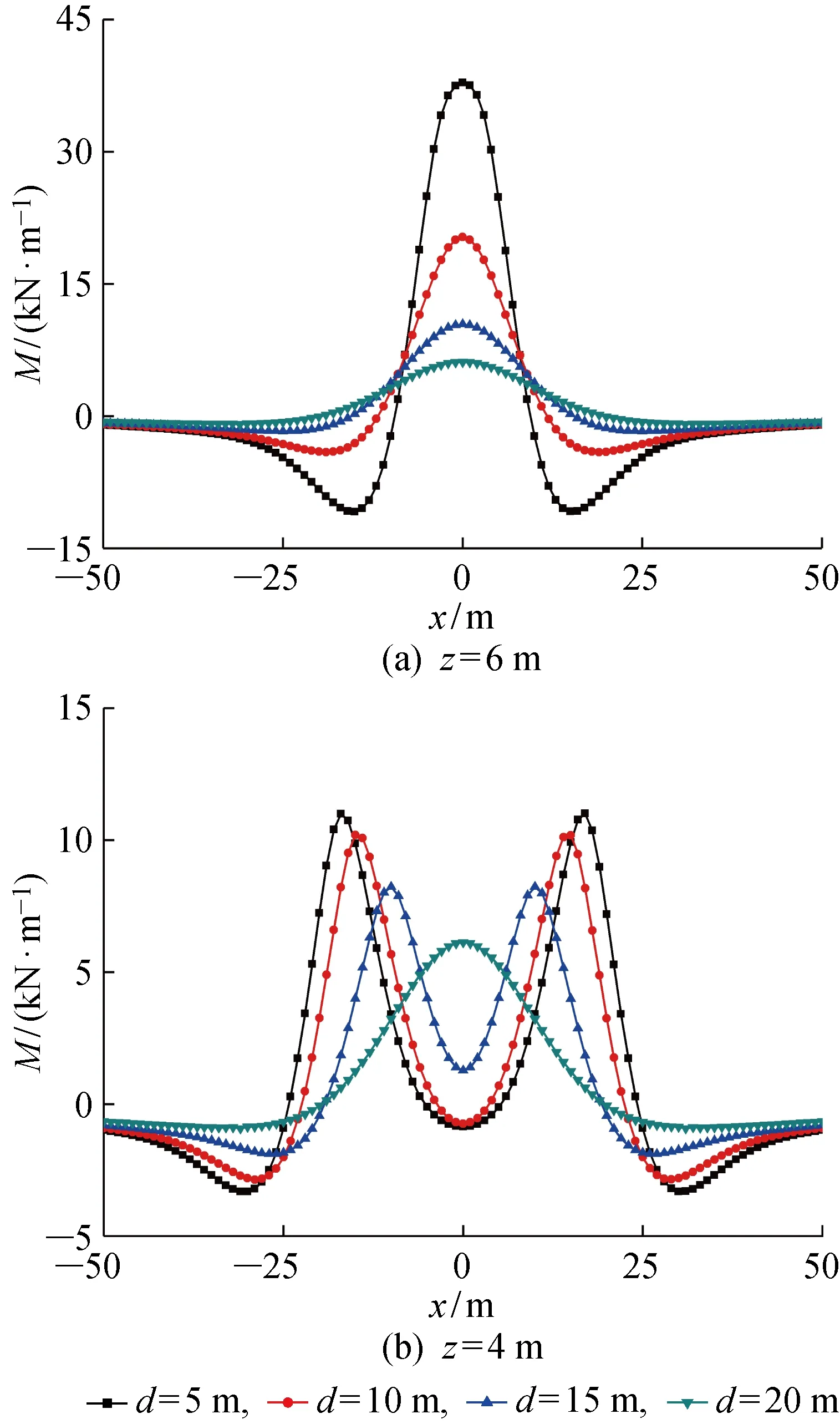
图17 降水井距管线不同距离时的管线弯矩Fig.17 Bending moments of pipeline at different distances from dewatering well

上述现象是由于当管线埋深较浅时，d较小时降水曲面与管线相交，部分水位降到管线以下，该部分管线所受附加荷载恒定，故d较小时管线变形基本不随d变化，管线弯矩为两个峰值，再次验证了前文提出的管线与水位线相交处会出现弯矩峰值.d增大到一定值后，降水曲面位于管线上方，水位线与管线不再相交，此后附加荷载分布形式随d变化将与管线埋深较浅时相似，管线变形及受力随d变化将呈现图16(a)、17(a)的趋势.此定值可由管线与水位线恰只有一个交点计算得出，为

(39)

4 结论

为了能反映降水引起的管线附加荷载空间变化以及管-土相互作用时土体的剪切效应，本文基于 Pasternak 弹性地基梁理论推导了一种单井降水引起邻近管线变形的解析计算方法，并通过降水试验及数值模拟验证其准确性.进一步对不同参数的敏感性展开了算例分析，研究了单井降水引起邻近管线受力变形的规律及机理，得到以下结论：

(1) 降水引起的邻近管线位移可达厘米级，可见工程中预降水对管线带来的影响不可忽略.参数分析中，土体剪切刚度对弯矩影响可达27%，证明了在研究管-土相互作用时，土中剪力的影响不应被忽略.

(2) 管线变形范围与影响半径大致相等，但变形较大值分布在影响半径25%范围内，应对管线中心段的变形进行重点监测及保护.

(3) 管线变形和弯矩最大值随降水井降深sw增大而增大，但存在一个临界降深，当sw达到临界降深后，弯矩最大值随着sw增大而减小，由中心向外偏移，出现两个弯矩峰值，弯矩峰值位于水位线与管线相交点附近，故对管线进行监测及保护时要注意水位线与管线相交处.

(4) 管线与降水点距离d对管线变形影响很大，降水点应尽可能远离管线，距离降水井越远，管线变形越小，弯矩越小.当埋深较浅且d较小时，管线弯矩有两个峰值，但会随着d增大逐渐减小并回归为一个峰值.