上方长距离基坑开挖引起的共线隧道变形研究

陈 拴，吴怀娜，陈仁朋，沈水龙，刘 源

(1. 湖南大学 土木工程学院， 长沙 410082； 2. 汕头大学 工学院， 广东 汕头 515063)

近年来，我国各大城市掀起了轨道交通建设的高潮，截至2019年底，我国共有44个城市开通轨道交通.同时，由于城市建设和改造速度的加快，已建地铁沿线出现了大量新建、改建和扩建的工程项目.地铁隧道多采用盾构法修建，盾构隧道的衬砌是由管片通过螺栓拼接而成，其变形控制要求往往达到毫米级.邻近工程建设不可避免会引起地层扰动，使既有隧道产生变形[1]，过大变形可导致管片开裂、渗漏水及道床脱开等病害，严重时甚至可能引发列车安全事故.近年来，由于邻近施工诱发的隧道破坏事故屡见不鲜，如台北捷运线邻近基坑开挖导致连续60余环衬砌道床脱离达20 mm，41环衬砌因受损严重[2-3].宁波地铁1号线[4]因邻近基坑开挖导致左线隧道375环范围出现不同程度的接头变形、渗漏水及管片开裂.上述安全事故多以侧方基坑开挖为主.然而，近年来一些城市修建的城市快速道路、综合管廊等使得地铁隧道上方出现长距离共线基坑开挖工程.隧道上方基坑开挖将导致下方土体应力释放、地层回弹，进而引发既有隧道产生上浮变形，而长距离基坑开挖的影响尤为严重，相关的研究仍鲜见报道.

针对基坑开挖引起的隧道变形预测，国内外学者采用现场实测[2-4]、数值模拟[5-8]、模型试验[9-10]以及理论分析[11-14]等方法开展了大量研究.其中，理论分析方法由于概念清晰，适用性广，具有重要的研究意义和实用价值.现场实测及反分析表明，盾构隧道纵向变形是由管片环刚性转动引起的弯曲变形、环间错台变形共同组成的[15-16].现有纵向理论模型可分为两类[16]：① 纵向管片环-接头模型，采用梁单元或壳单元模拟管片环、弹簧模拟接头；② 纵向等效连续化模型，将隧道简化为均质梁并通过等效刚度考虑环间接头的刚度弱化效应.相比之下，纵向等效连续化模型由于计算简单而被广泛采用.然而，传统的纵向等效连续化模型通常将隧道简化为均一刚度的欧拉伯努利梁，即假设隧道为纯弯变形，与实际不符.Wu等[16]基于铁木辛柯梁理论建立了能同时考虑弯曲变形和剪切错台的纵向结构模型，并给出了环间张开量和错台量的确定方法.

本文在Wu等[16]提出的隧道纵向铁木辛柯梁简化模型的基础上，引入Winkler地基模型，提出了一种上方基坑开挖引起隧道变形的解析模型，进而利用叠加原理推广至长距离共线基坑开挖对隧道的影响分析.依托深圳某长距离共线基坑工程，验证本研究模型的有效性，并进一步探讨了长距离基坑开挖对下方隧道上浮变形和渗漏水的影响机制.

1 上方基坑开挖引起隧道变形解析模型

本文采用2阶段分析法分析上方基坑开挖引起的共线隧道纵向变形和接头变形.阶段1：假定土体为弹性半无限空间的弹性体，隧道为无限长连续体，不考虑既有隧道的影响，采用Mindlin弹性解计算基坑开挖引起的土体附加应力.阶段2：将隧道纵向的铁木辛柯梁简化模型[16]与Winkler地基相结合，建立土-隧道相互作用模型，将阶段1附加应力施加于隧道上，进而获得基坑开挖引起的隧道纵向变形和内力的解析解.

1.1 基坑开挖引起的隧道附加应力

图1为基坑与隧道相对位置平面图，分别以基坑平面中心O′和隧道中心O为原点建立ξ′-η′全局坐标系和x-y局部坐标系，OO′为原点连线，O′x′为x轴的平行线，χ为ξ′轴与x轴之间的夹角，s为原点连线OO′的长度，υ为ξ′轴与原点连线OO′之间的夹角，χ、υ均以逆时针旋转为正，反之为负.

图1 基坑与既有隧道相对位置平面图Fig.1 Plan of relative position of excavation and existing tunnel

基坑开挖引起的隧道上任意位置(x，y)的附加应力f(x，y)为

(1)

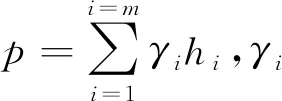
其中，X、Y为计算点在ξ′-η′全局坐标系下的坐标，与x-y局部坐标系之间满足：

X=xcosχ+ysinχ+scosυ

(2)

Y=-xsinχ+ycosχ+ssinυ

(3)

基于Mindlin解的附加应力计算方法，可以考虑不同相对位置对隧道的影响.

1.2 土-隧道相互作用模型

Wu等[16]基于铁木辛柯梁理论提出了考虑剪切错台变形的纵向等效连续化模型.该模型把隧道理想化为一个均质的铁木辛柯梁，采用综合考虑衬砌环和接头影响的等效弯曲刚度和等效剪切刚度.图2为隧道纵向的铁木辛柯梁简化模型示意图.图中：M、Q分别为弯矩和剪力；ls为管片环宽度；lb为螺栓长度；abcd和cdef分别表征变形前管片单元和接头单元的形状；abc′d′和c′d′e′f′分别表征变形后管片单元和接头单元的形状；θ、θs及θj分别为弯矩作用下计算单元的转角、混凝土管片环的转角及环缝引起的转角；u、us及uj分别为剪力作用下计算单元的位移、混凝土管片环的位移及环缝引起的位移.

图2 隧道纵向的铁木辛柯梁简化模型示意图[16]Fig.2 Illustration of Timoshenko beam simplified model of tunnel in longitudinal direction[16]

根据铁木辛柯梁理论，隧道满足以下平衡方程、几何方程和物理方程[17]：

(4)

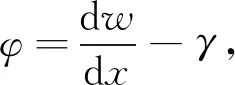
(5)

M=(EI)eqkc,Q=(κGA)eqγ

(6)

式中：M′、M″为分别为弯矩的一阶、二阶导数；q为外荷载；φ为管片环旋转角；w为隧道中性轴的竖向位移，即隧道上浮变形；γ为剪切角；kc为中性轴的曲率；(EI)eq为隧道纵向等效弯曲刚度，其中E为弹性模量，I为第二惯性矩；(κGA)eq为隧道纵向等效剪切刚度，其中κ为铁木辛柯剪切系数(对于环形隧道，κ=0.9)，G为切变模量，A为管片环横截面积.

(EI)eq及(κGA)eq基于几何等效确定，其计算公式如下[16]：

(7)

(8)

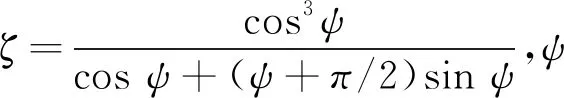
Wu等[16]进一步推导环缝的最大张开量Δ、环间最大错台量δ的计算公式如下：

(9)

(10)

式中：r为隧道半径.

本文在Wu等[16]提出的隧道纵向铁木辛柯梁简化模型的基础上，引入Winkler地基，建立土-隧道相互作用模型，并给出外荷载作用下隧道内力和变形的解析解[19].图3为Winkler地基-铁木辛柯梁模型示意图，图中q(x)为纵向x位置作用在隧道的外荷载.

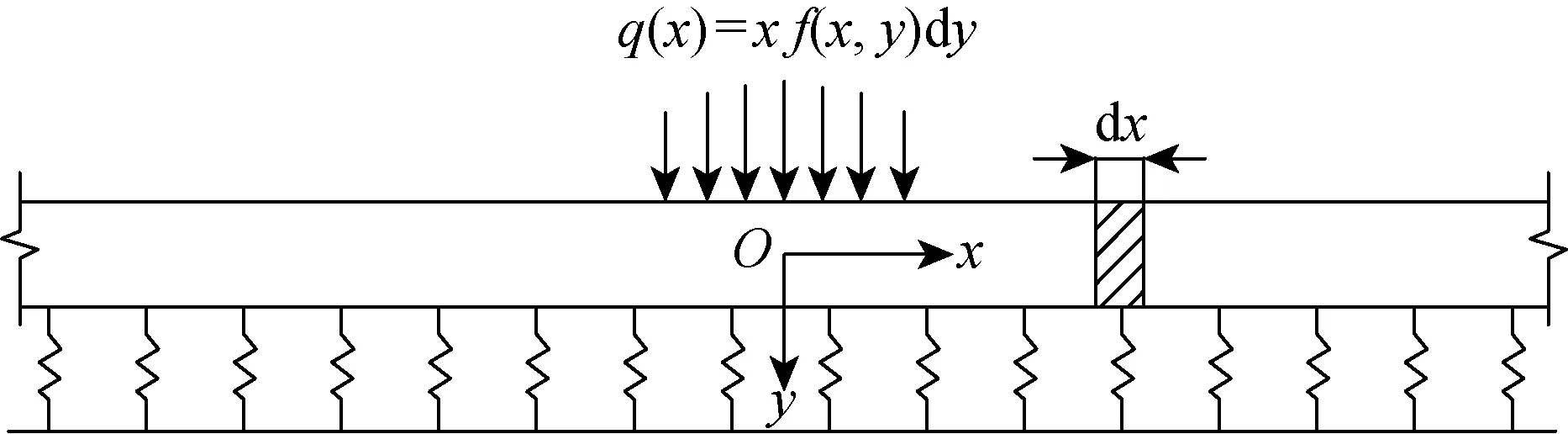
图3 Winkler地基-铁木辛柯梁的土-隧道相互作用模型示意图Fig.3 Illustration of soil-tunnel interaction model of Winkler foundation-Timoshenko beam

取足以覆盖隧道影响范围的纵向计算长度L作为模型分析范围.将作用在隧道纵向上的外荷载q(x)以Fourier级数展开，即

(11)

由铁木辛柯梁理论和弹性地基梁理论可得Winkler地基上有限长梁的力的平衡方程为

(12)

式中：ke为等效地基土压缩基床系数，ke=2kr，k为地基土基床系数.

将式(4)、(5)代入式(12)，并令D=(EI)eq，C=(κGA)eq，由此可得：

(13)

(14)

由(13)、(14)推导得Winkler地基上铁木辛柯梁变形控制方程：

(15)

将式(11)代入上式，则w的通解为

w=(c1cosβx+c2sinβx)eαx+

(c3cosβx+c4sinβx)e-αx+

(16)

式中：c1～c4为常数；α、β、dn分别为

(17)

(18)

(19)

上式仅在ke<4C2/D时成立，当ke≥4C2/D时，令式(18)中β为iβ.

梁任意截面的旋转角为

φ=(c5cosβx+c6sinβx)eαx+

(c7cosβx+c8sinβx)e-αx+

(20)

式中：

(21)

(22)

(23)

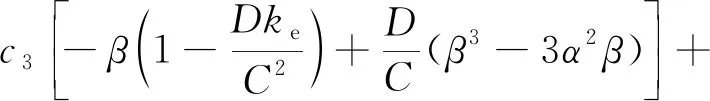
(24)

上述w和φ表达式中c1～c8可通过以下边界条件确定：

(25)

当c1～c8确定后，w和φ即可得出，则M和Q可由式(4)～(6)求得.已知M、Q后，由式(9)、(10)确定管片环的张开量和错台量.

2 工程实例分析

2.1 工程概况

深圳某地下快速道路基坑工程与既有地铁隧道长距离共线，共线段达3.09 km，基坑采用明挖法施工，主体段开挖宽度39.7～46.0 m，局部宽度达52.0 m，开挖深度8.4～16.3 m，隧道拱顶距离基坑底板6.2～14.9 m.基坑围护结构为钻孔灌注桩，直径1.0 m，间距1.2 m.图4为典型断面I基坑与隧道相对位置关系图.该断面基坑开挖宽度和深度分别为46.0 及16.3 m，左线隧道距离基坑围护结构8.0 m，左、右线隧道轴线间距13.0 m，基坑底板与隧道拱顶最小垂直距离为6.2 m.表1为隧道衬砌和螺栓参数，表中De和t分别为隧道外径和衬砌厚度；νs为混凝土衬砌的泊松比；Db、Eb和νb分别为纵向螺栓直径、弹性模量和泊松比.

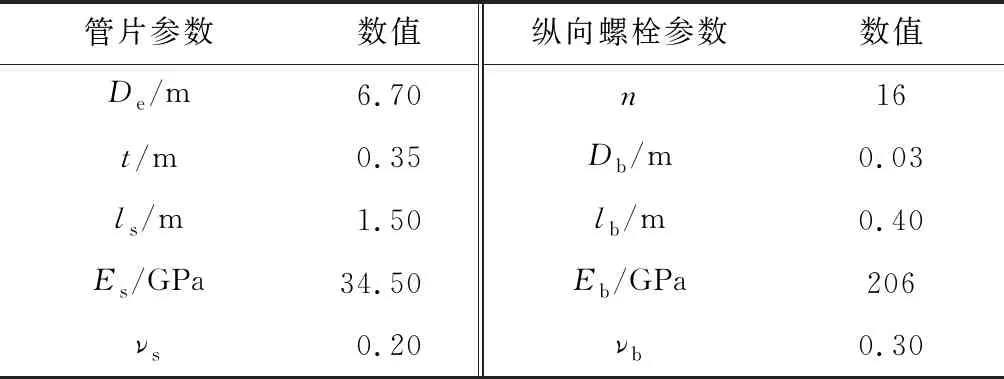
表1 隧道衬砌和螺栓参数Tab.1 Parameters of segmental lining and bolt

图4 典型断面I基坑与隧道相对位置(m)Fig.4 Relative position between excavation and tunnel for typical section I (m)

本文取该工程其中340 m共线段进行分析，图5为其地质剖面图.场地上覆土层为素填土，填砂或

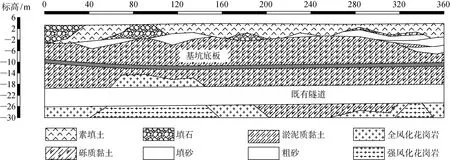
图5 隧道沿线地质剖面图Fig.5 Geological section along tunnel

填石交替出现，局部夹杂淤泥质黏土粗砂.其下为厚度3～12 m的砾质黏土层，下伏全风化和强风化花岗岩.基坑底板全部位于砾质黏土层，隧道下卧土层为砾质黏土或全风化花岗岩.表2为场地土层物理力学参数.表中：γs为土体天然重度；e0为孔隙比；w0为含水量；c0为黏聚力；φ0为内摩擦角；Es0为变形模量.

表2 土层物理力学参数Tab.2 Physical and mechanical parameters of soil layers

为减小长距离共线基坑开挖对既有地铁隧道的影响，土方开挖采用分层分段开挖方法.本文研究其中4个开挖工况，如表3所示，工况1-1表示第1个工况的第1个开挖步，1-2表示第1个工况的第2个开挖步，以此类推.表中Le和He分别为开挖长度和开挖深度.现场对隧道变形进行实时监测，并对隧

表3 开挖工况Tab.3 Excavation conditions

道渗漏水情况进行调查.在工况4-4主体结构施工完成后，首次发现左线隧道193～212 m多处发生不同程度渗漏水，断面I (即207 m处)最大上浮量达20.5 mm，超过变形控制标准值(20.0 mm)，其内弧面管片局部压溃脱落，接头渗漏严重.右线隧道位于围护结构外侧，基坑开挖引起的上浮量小(不超过 5.0 mm)，无渗漏水现象.

2.2 结果分析

2.2.1模型验证 基于本文提出的Winkler地基-铁木辛柯梁模型对该工程变形较为严重的左线进行分析.根据表1所获得隧道弯曲刚度有效率η=1/7，剪切刚度修正系数ξ=0.68，并由式(7)、(8)确定 (EI)eq=1.83×108kN·m2，(κGA)eq=1.97×106kN.根据主体结构截面形式所得的结构荷载为Ps=130 kPa.并且由步骤3通过反演分析可以确定出砾质黏土和全风化花岗岩的基床系数分别为13.44 MPa/m 和21.0 MPa/m，将上述参数代入所提的土-隧道相互作用模型，可得不同开挖工况下的隧道变形和内力.对分段开挖引起的隧道变形，分别计算各段引起隧道变形和内力，并通过叠加的方法确定总变形量和总内力.

图6为计算的隧道上浮量与实测结果对比图，图中S为距离.由图可知，隧道上浮变形理论计算结果与现场实测均呈现双峰状，工况4-4施工完成后隧道最大上浮量达20.5 mm，与理论计算的最大上浮量20.3 mm较为接近.二者从趋势和幅值上均较为吻合，表明本文提出的土-隧道相互作用模型能较好地预测上方基坑开挖引起的隧道变形，同时说明基于叠加原理分析长距离开挖引起的共线隧道变形是合理的.根据图6可以判断，基坑开挖到底时，其变形影响范围可延伸到开挖范围外侧40 m左右.

图6 隧道变形理论计算结果与现场实测结果对比Fig.6 Comparison of theoretical calculation results of tunnel deformation with field measured results

2.2.2隧道渗漏水分析 现场观测表明工况4-4主体结构施工完成后出现隧道渗漏水，而此前并未观测到渗漏水.为探明其原因，将工况4-3和4-4下的隧道内力和接头变形进行对比，如图7所示.由图7(a)可知，长度为40 m的主体结构施工完成后，约80 m范围隧道结构上浮变形显著回落，最大减小量达11.4 mm，但局部出现沉降槽，差异沉降量约为10 mm/40环.

图7(b)、 7(c)为隧道弯矩和剪力图.可知，主体结构施工后，内力显著增大，其变化范围约 110 m.主体结构范围内隧道弯矩由504.7 kN·m变成-3 160.9 kN·m，两侧弯矩峰值由 3 624.9 kN·m 变成 5 549.1 kN·m.剪力方向不变，两侧最大剪力由148.5 kN和-92 kN提高到363.5 kN和-350.1 kN.由图7(d)、7(e)为主体结构施工前后接头变形图.由图可见，接头张开量和错台量的变化趋势与隧道弯矩和剪力相对应，较之主体结构未施工时，环缝弯曲张开和剪切错台量显著增加.

图7 主体结构施工前后隧道内力和接头变形Fig.7 Joint deformation and internal force of tunnel before and after construction of structure

图8为工况4隧道上浮变形、接缝变形与渗漏水位置关系图.隧道在193～212 m出现连续渗漏，主要位于环与环之间接缝.对比渗漏区域与隧道变形可以发现，渗漏区域并非位于上浮最大值处，因为此处隧道上浮量虽大，但接缝变形表现出张开量大、剪切变形量小的特点.渗漏区域主要位于接缝张开量最大值与接头错台变形最大值之间.同时，也进一步说明隧道渗漏水是由弯曲变形和剪切变形共同作用所致，即隧道纵向变形是弯曲张开、剪切错台兼而有之.传统的模型将隧道变形简化为纯弯模式，忽略了环间剪切变形，将导致计算结果的不准确性.

图8 工况4-4隧道接缝变形与渗漏水位置分析Fig.8 Analysis of tunnel joint deformation and water leakage location for 4-4

2.2.3隧道剪切变形占比 隧道的弯曲和剪切变形机理不同，前者由管片环刚体旋转，环缝张开变形为主，后者则由管片环与环错台累积而成.本节进一步探究两者在隧道上浮变形中发挥的作用.图9为工况4-4时w、弯曲变形wb、剪切变形ws沿纵向分布图.可以看出，剪切变形占总变形的比例最大仅21.72%，但根据上节接缝变形分析，其引起的接缝错台变形最大值较弯曲引起的最大张开量更大，其对渗漏水的影响有着重要的影响.表4统计了不同工况下隧道上浮变形达到峰值时剪切变形的占比P.由表4可知， 当隧道上浮变形达到峰值时剪切变形的占比一般为21.72%～27.04%，隧道上浮变形达到最大时剪切变形的平均占比为21.41%.

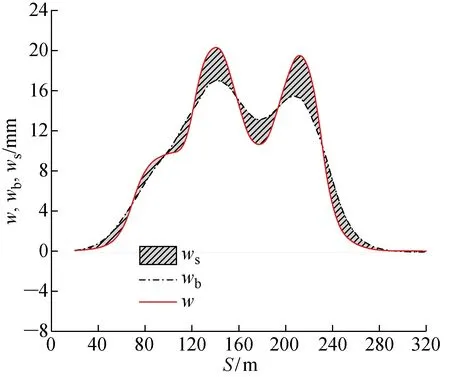
图9 工况4-4的隧道纵向变形Fig.9 Longitudinal deformation of tunnel under excavation condition of 4-4

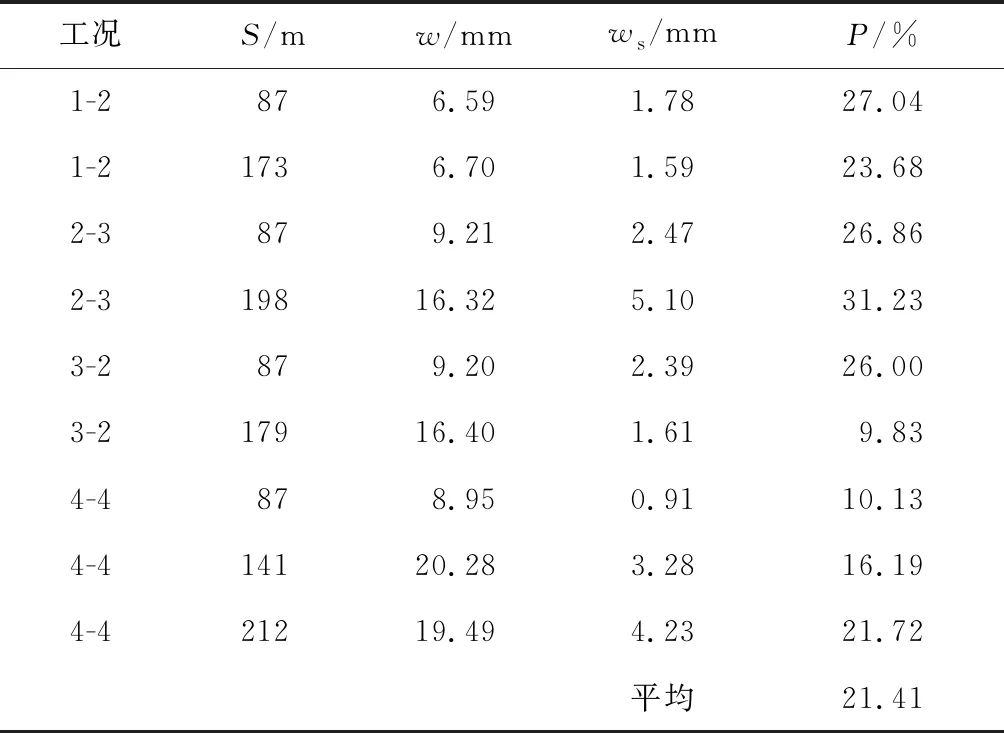
表4 剪切变形与隧道最大上浮变形的占比

3 结论

本研究提出了一种用于分析上方基坑开挖引起的共线隧道结构变形的解析模型，结合深圳某长距离共线基坑开挖工程进行分析，得出如下结论：

(1) 基于考虑隧道剪切错台的铁木辛柯梁简化模型，引入Winkler地基模型，提出了一种上方基坑开挖下土-隧道相互作用解析模型，推导了其在任意荷载下的解析解.利用叠加原理将该模型推广至上方长距离基坑开挖引起的共线隧道变形分析.通过实例分析表明本研究模型具有较好的合理性，同时上方基坑分段开挖引起的共线隧道上浮变形满足叠加原则.

(2) 主体结构施工后，隧道上浮变形明显回落，但局部差异沉降增加，导致隧道内力显著增大，环缝接头张开量和错台量明显增加.隧道渗漏水位置并非位于隧道上浮变形最大处，而是位于接头张开量最大处与接头错台变形最大处之间.进一步说明隧道变形是由接缝弯曲张开和环间错台共同作用所致.实际工程中不应仅关注隧道总变形，同时应关注接缝张开及错台变形.

(3) 通过统计不同工况下隧道上浮变形达到峰值时剪切变形所占比例发现，隧道上浮变形最大处剪切变形仅占21.72%～27.04%，平均占比为21.41%，但其引起的接缝错台变形最大值较弯曲引起的最大张开量更大，其对接缝防水有重要影响.理论模型中考虑剪切错台变形的影响十分重要.