动载荷下含水率对黄砂岩的分形特征及比表面能的影响

侯文光，秦金辉

1.霍州煤电李雅庄煤矿，山西 霍州031400；2.河南理工大学安全科学与工程学院，河南 焦作454003

水分对岩石的物理力学性能有重要的影响［1］，水分在岩石内部容易对岩石产生物理［2-5］及化学［6］作用，这些作用对于岩石的力学特征及能量耗散等有重要影响。随着地下工程及煤炭的深部开采等一系列岩土工程的需要，常常需要对地下岩石进行爆破类的动载荷作用，由于不同岩层的含水情况不同，导致岩石受到相同的动载荷作用时破碎情况有所差异，该差异的内因是由于岩石内部的比表面能变化所引起。因此将含水率作为突出变化因素，研究含水率对岩石比表面能的影响有重要意义。

目前关于岩石含水情况下的物理力学性能及能量耗散等一系列性质研究成果很多。不同含水率岩石动静力学试验表明，含水率的变化对岩石的力学性能有重要影响［7-8］。吴勇［9］研究发现岩样直剪强度参数C、φ随含水率的增加而减小，且C值对水的反应比φ值敏感。王斌等［10］对长径比为0.5的开阳磷矿砂岩进行自然风干和饱水状态下的静载和冲击压缩试验，发现中应变率加载条件下，自然风干砂岩动态屈服应力与其静态相近，饱水砂岩动态屈服应力比其静态下的结果可提高近2倍，表现出比风干岩石更强的应变率敏感性。

含水率对岩石能量耗散规律与损伤变量的影响受到国内外学者的广泛关注［10-12］。李天斌等［13］利用MTS815对5种含水率（ω=0，ω=0.2ωs，ω=0.5ωs，ω=0.7ωs，ω=ωs，其中ωs为饱和质量含水率）分别开展围压20、30、40 MPa下的常规三轴压缩试验，发现随含水率的增大，岩石吸收的总能量及其增速减少，弹性能在储能阶段随含水率的增加而减少。郭佳奇等［14］研究了自然与饱和水状态下的能量机制，发现饱水试样吸收的总应变能小于自然状态试样吸收的总应变能。段天柱等［15］在单轴压缩试验中发现损伤变量随含水量的升高而增加。一系列研究表明含水率变化对岩石的能量及损伤有重要影响。

大量的研究揭示了含水率对岩石的影响规律，然而大多数关注点侧重于其物理力学性质、能量耗散、损伤等方面，对于上述现象发生的本质即含水率变化对岩石比表面能的影响研究较少。霍州煤电李雅庄矿在岩巷掘进生产过程中，涉及到不同含水率黄砂岩的动载荷问题，因此本文利用霍普金森压杆对6种不同含水率黄砂岩进行动态冲击，对试验后的碎块进行统计分析，同时将其转化为对应粒径范围内的球体，并结合冲击过程的耗散能，研究含水率变化对黄砂岩的分形维数、损伤、能量耗散及比表面能的影响。研究结果对于解决岩土工程中涉及到的动力学相关问题有重要的指导意义。

1 试验部分

1.1 试样制备

试样采自霍州煤电李雅庄矿深度约550 m处的黄砂岩。原始的黄砂岩经过钻芯机取样-切割机切割-球磨机打磨等流程后，最终制成50 mm×50 mm（直径×高）的圆柱体试样。

将制备好的黄砂岩试样置于105℃的恒温箱中烘干24 h，称量烘干后黄砂岩的质量，重复多次，直至前后两次的质量差小于0.01 g，认为此时黄砂岩干燥。将干燥的黄砂岩置于不同湿度的恒湿箱中24 h，然后称量吸水后黄砂岩的质量，重复多次直至其前后两次质量差小于0.01 g，即认为达到设定的含水率。

1.2 试验方法

试验设备采用霍普金森压杆试验系统，该系统包括气体控制装置、入射杆、反射杆、透射杆、信号采集系统等。

试验前，利用霍普金森压杆试验系统对黄砂岩在不同冲击气压下进行冲击，分析冲击后的试验数据，并结合现场实际情况，将冲击气压定为0.21 MPa。

试验时：首先，将吸水后不同含水率黄砂岩试样两端涂抹一定量的凡士林，减少端部摩擦效应；其次，打开气体控制阀，在发射腔内注入氮气直至气压达到0.21 MPa，关闭气体控制阀，打开发射控制阀，完成撞击。试验过程中数据通过入射杆和透射杆上的应变片收集。

2 不同含水率黄砂岩碎块分布及其分形维数

2.1 不同含水率黄砂岩碎块的粒径分布

为了更加直观地分析含水率变化对黄砂岩的碎块分布的影响，利用分级筛对不同含水率黄砂岩碎块进行筛分，分级筛网格的孔径分别为3.00、2.00、1.50、1.20、1.00、0.50、0.30、0.25 mm，最终收集到粒径范围为5.00～3.00、3.00～2.00、2.00～1.50、1.50～1.20、1.20～1.00、1.00～0.50、0.50～0.30、0.30～0.25、0.25～0 mm范围内的碎块。

式中，wi为该粒径下碎块所占质量分数，mi为该粒径下碎块的质量，md为试块总质量。

首先，定义筛分后各级碎块质量mi与试样初始总质量md的比为试样碎块质量分数wi；然后，将各分级组的碎块平均粒径di与该粒径下碎块质量分数wi相乘，获得该级碎块的粒径分布δi；最后将该试样各级碎块的粒径分布δi进行累加，可求得该试样破碎后的平均粒径δ，相关计算表达式［16］为：

式中，i为分级筛等级数，i=1，2，3……9；di为每级筛分碎块的平均粒径，取分级筛上、下两级的平均筛孔尺寸计算。

利用式（1）和式（2）对不同含水率下黄砂岩的碎块进行计算，可得到其不同粒径范围内碎块的质量分数，以及不同含水率下黄砂岩碎块的平均粒径，如表1所示。

表1 不同含水率下黄砂岩碎块的粒径分布Tab.1 Size distribution of yellow sandstonefragmentswith different water contents

图1为不同含水率黄砂岩的碎块分布。从图1中可以看出含水率变化对于黄砂岩的碎块分布有重要影响：含水率较低时，黄砂岩的碎块主要分布在较大粒径范围内，随着含水率的升高，黄砂岩碎块分布逐步向小粒径范围内发展；黄砂岩的平均粒径随着含水率的升高逐步减小，表明水分含量越高的情况下，在相同的冲击作用下，黄砂岩的破坏越严重。

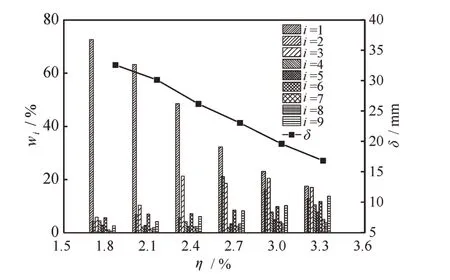
图1 不同含水率下黄砂岩的碎块分布Fig.1 Fragment distribution of yellow sandstone with different water contents

2.2 不同含水率黄砂岩碎块分形维数的计算原理

大量关于岩石类破碎情况的研究中，发现利用分形几何学可以将破碎无规则的试验碎块转换成可以描述的数据，从而将试验过程中碎块分布规律进一步量化［17-19］，而利用质量-等效尺寸方式的分形维数算法是一种简单有效的方式，具体计算过程如下［20-21］：

式中：D为碎块的分形维数，d为双对数坐标下所绘制直线的斜率，mR为直径小于R的碎块累计质量。

2.3 含水率变化对黄砂岩分形维数的影响

根据式（3）可以计算不同含水率黄砂岩试验碎块质量分形维数与等效粒径分形维数的关系，如图2所示。从图2中可以看出，不同含水率下砂岩碎块质量分形维数与等效粒径分形维数的斜率分布有所差异，斜率随含水率增加而降低，含水率越大，斜率越小。当含水率为1.8%时，黄砂岩碎块质量与等效粒径分形维数的斜率为1.125 0，随着含水率的升高，当含水率为3.3%时，黄砂岩碎块质量与粒径分形维数的斜率为0.683 7。

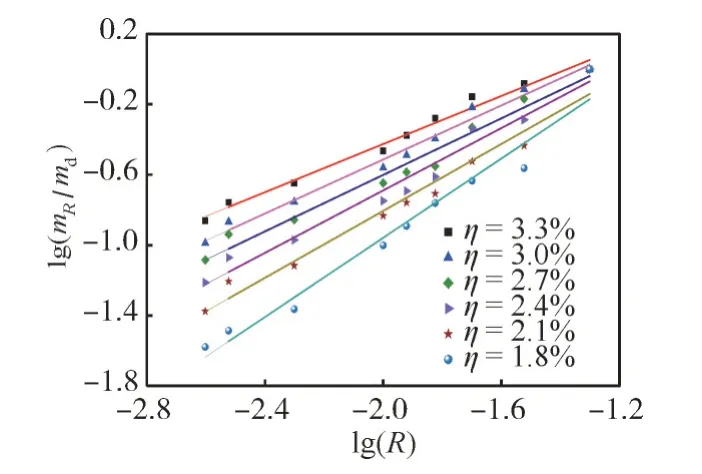
图2 试验碎块的质量与等效粒径分形维数的关系Fig.2 Relationship between mass of test pieces and fractal dimension of equivalent particle size

图3为黄砂岩的分形维数D随含水率的变化规律。从图3中可以看出，随着含水率的升高，黄砂岩的分形维数D逐渐增加。当含水率为1.8%时，黄砂岩的分形维数D为1.875 0，随着含水率逐渐上升到3.3%，此时黄砂岩的分形维数为2.316 3，较含水率为1.8%时的分形维数增幅23.54%。由黄砂岩的分形维数随含水率变化可以看出，水分的增加使得黄砂岩在受到冲击时，其完整性更加容易破坏。

图3 黄砂岩的分形维数D随含水率的变化规律Fig.3 Variation of fractal dimension of yellow sandstone with water content

3 含水率对黄砂岩能量变化的影响

3.1动载荷作用下黄砂岩的能量计算原理

黄砂岩在进行冲击载荷过程的变形破坏为典型的物理变化，其实质是将积聚的机械能转化为耗散能等能量的动态过程。因此应力波所携带能量通过式（5）［21-22］计算：

式（5）中，A为入射杆与透射杆的横截面积，为1 963.49 mm2；E为入射杆与透射杆的弹性模量，为210 GPa；C为一维应力波波速。由于入射杆和透射杆皆为刚体，因此，C与入射杆的密度和弹性模量E相关，二者之间的关系可用式（6）［14-15］表示：

根据式（5）和式（6），霍普金森压杆试验动态冲击过程中入射能WI、反射能WR和透射能WT可表示［14-15］为：

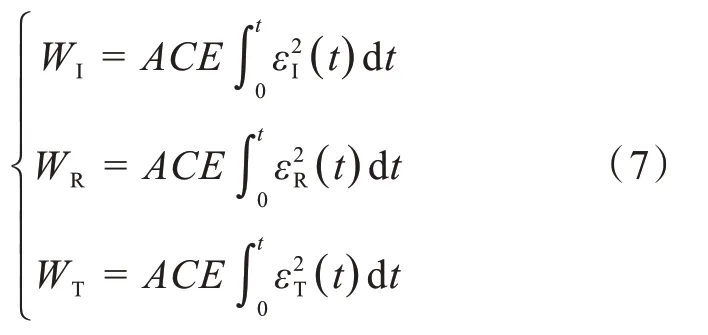
式（7）中，WI、WR、WT分别为入射能、反射能、透射能。

由入射能、反射能和透射能之间的关系最终可获得砂岩在冲击破坏时的耗散能WL，如式（8）所示［20-21］：

3.2含水率对黄砂岩各能量变化的影响

图4（a）为黄砂岩中各能量随含水率的变化规律。由图4（a）可以看出：随着含水率的升高，黄砂岩的反射能逐步升高，透射能和耗散能逐步降低；当含水率为1.8%时，黄砂岩的反射能为12.18 J，含水率升高到3.3%，黄砂岩的反射能为30.39 J，较含水率为1.8%增幅149.51%；当含水率为1.8%时，黄砂岩的透射能为22.61 J，随着含水率升高到3.3%，黄砂岩的透射能为9.38 J，较含水率为1.8%降幅58.51%；当含水率为1.8%时，黄砂岩的耗射能为9.36 J，随着含水率升高到3.3%，黄砂岩的耗散能为4.61 J，较含水率为1.8%降幅50.75%。通过对反射能、透射能和耗散能与含水率之间进行拟合发现，三者与含水率的变化呈线性关系。

能量的变化说明含水率变化对黄砂岩的能量耗散有重要影响，这是由于随着含水率的增加，水分降低了黄砂岩内部颗粒间彼此的黏结力，从而使得黄砂岩软化，而黄砂岩受冲击破坏过程本身是一种能量的积聚与释放过程，颗粒间的黏结力的降低，使得颗粒需要更少的能量就可以彼此分离。同时，随着含水率的增加，水分与黄砂岩内部的矿物质成分作用，溶解了部分胶结物，降低了黄砂岩整体结构的完整性［13］。这些变化反应到黄砂岩的能量耗散过程中表现为不同含水率下各能量有所差异。

图4 黄砂岩中（a）各能量和（b）比表面能随含水率的变化规律Fig.4 Variation rule of（a）energy and（b）specific surface energy with water content in yellow sandstone

3.3 黄砂岩比表面能计算原理

岩石为脆性材料，耗散能主要是以使碎块彼此分离的比表面能的形式耗散掉［22］，为了进一步探究含水率变化对黄砂岩的比表面能的影响，将不同粒径下的碎块简化为球体，将砂岩碎块简化成筛分对应尺寸的球体［22］。在筛分的直径范围内球体的数量按式（9）计算［22］：

式（9）中，ni为尺寸i下球体的数量，mi为尺寸i下球体的质量，ρ为黄砂岩的密度，为2 395 kg/m3，ri为尺寸i转化的球体半径。

利用式（9）并结合不同粒径下碎块质量mi可以计算得到尺寸i下球体的数量ni，所有尺寸球体的表面积之和减去试验前圆柱体的上下表面积及侧面积之和，即为黄砂岩破坏面的面积之和，计算如式（10）所示［22］：

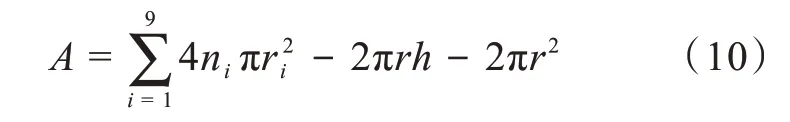
式（10）中，r为冲击试验中砂岩试块的半径，h为冲击试验中砂岩试块的高度。

黄砂岩在受到冲击作用时，输入的动能逐步转化为内部积聚的能量，这些能量导致黄砂岩碎块彼此分离，而所有碎块彼此分离所需要的能量之和即为外界的输入能量。黄砂岩自身作为一种脆性材料，耗散能可以视为黄砂岩破碎时所需的比表面能，因此比表面能与耗散能的关系为［22］：

式（11）中，γ为比表面能，即碎块彼此分离时单位面积所需的能量。

由于耗散能大部分作用为使界面彼此分离，利用耗散能与碎块的表面积之间的关系，可求得单位面积上黄砂岩碎块的比表面能［22］：

3.4含水率对黄砂岩比表面能变化的影响

图4（b）为黄砂岩的比表面能随含水率的变化规律。由图4（b）可知，随着含水率的升高，黄砂岩的破碎表面积逐步增加，当含水率为1.8%时，黄砂岩的破碎表面积为169.89 cm2，含水率升高至3.3%，黄砂岩的破碎表面积为510.00 cm2，较含水率为1.8%时增幅200.19%；随着含水率的升高，黄砂岩的比表面能逐步减小，当含水率为1.8%时，黄砂岩的比表面能为0.06 J·cm-2，随着含水率升高到3.3%，黄砂岩的破碎表面积为0.01 J·cm-2，较含水率为1.8%时降幅83.59%。

比表面能随含水率的变化说明含水率对于黄砂岩的比表面能有重要影响。这是由于水分降低了黄砂岩内部颗粒的黏结力，同时水分对于部分矿物质有溶解作用，含水率越高，溶解作用越明显，从而使得单位面积上黄砂岩颗粒彼此分离的能量越低。

4 结 论

利用霍普金森压杆对6种不同含水率黄砂岩在0.21 MPa气压下进行动态冲击，对冲击后的碎块进行筛分，并结合耗散能，得到碎块的分形维数、耗散能及比表面能与含水率的关系。

1）随着含水率的升高，黄砂岩碎块的质量-等效尺寸分形维数的斜率逐步升高，碎块的粒径分布由大粒径逐步向小粒径发展，黄砂岩的损伤逐步增大。水分增加降低了黄砂岩的比表面能，相同冲击气压作用下，碎块更容易彼此分离，导致碎块的整体粒径分布更小，黄砂岩破碎的越严重，分形维数越大。

2）随着含水率的升高，黄砂岩的反射能逐步增大，透射能和耗散能逐步减小。表明含水率对系统中能量的变化影响显著，水分降低了黄砂岩内部颗粒的黏结力及对黄砂岩内部矿物质的溶解，导致黄砂岩在相同的冲击气压下各能量有所差异。

3）随着含水率的升高，黄砂岩碎块的表面积逐步增加，比表面能逐步下降。水分的增加造成黄砂岩软化从而降低了黄砂岩颗粒彼此间的黏结力，溶解了黄砂岩内部的部分矿物质颗粒，因此随着含水率升高，黄砂岩单位面积上的颗粒需要更少的能量即可彼此分离。