共固化双层阻尼薄膜复合材料结构的阻尼性能∗

王绍清，梁 森，刘 鹏

（1.潍坊科技学院山东省高校设施园艺实验室 潍坊，262700）（2.青岛理工大学机械与汽车工程学院 青岛，266000）

1 问题的引出

共固化双层阻尼薄膜复合材料结构（co‐cured composite structures with double ‐ layer damping membranes embedded，简称CCSDDME）是在特定环境下将3 种不同性质的材料通过人工或现代工艺复合而成的一种多相固体［1‐6］。这3 种材料在性能上相互协调，大大提高了结构的阻尼性能，并获得了单一材料难以比拟的动力学性能。该结构在智能化温室、航天飞机、卫星和建筑等领域有着极其广泛的应用前景［7］。由于CCSDDME 具有可设计性，包括黏弹性阻尼材料、阻尼层几何尺寸、增强材料和基体材料种类等，这些为CCSDDME 的力学性能改善和极端使用环境提供了可能，其结构如图1 所示。

图1 CCSDDME 试件结构Fig.1 Structure of CCSDDME specimens

固有频率和损耗因子是共固化双层阻尼薄膜复合材料结构动力学性能的重要指标［8］。文献［9‐12］对单一阻尼层嵌入的连续阻尼结构动力学性能、隔声性能、疲劳性能以及低速冲击性能进行了研究。文献［13］利用模态应变能方法研究了嵌入式共固化穿孔阻尼层复合材料结构在不同参数下的固有频率和模态损耗因子。文献［5］按照固化过程工艺曲线制成了嵌入式中温共固化多层阻尼薄膜复合材料试样，并用模态应变能的方法研究了该结构的阻尼性能。文献［14］研发一种新型5层夹芯复合材料仪表板，并将该仪表板中心层和上、下蒙皮设计成共固化多层阻尼复合材料结构，通过模态实验和模态应变能有限元相结合的方法研究了黏弹性材料层和泡沫材料层厚度变化对固有频率和模态损耗因子的影响。综上所述，研究人员对单一阻尼层和多个阻尼层嵌入的共固化复合材料结构动力学性能的研究多采用模态实验和模态应变能有限元法，但模态应变能有限元法对单元依赖性较强，精确度浮动较大。利用Rayleigh‐Ritz 可以较精确地求解结构的固有频率和损耗因子。

笔者应用Rayleigh‐Ritz法研究了结构的动力学性能，并计算了结构的固有频率和损耗因子，得到了固有频率和损耗因子随阻尼层位置和剪切模量的变化规律，为轻质大阻尼复合材料结构设计提供了理论支撑。

2 CCSDDME 固有频率和损耗因子的推导

为了得到控制方程，假设如下：①CCSDDME在厚度方向的变形忽略不计；②CCSDDME 每层界面之间不发生滑移；③CCSDDME 各层之间的位移关系符合1 阶剪切变形理论；④CCSDDME 中黏弹性层具有相同的力学性能，剪切模量采用复常数模量。CCSDDME 面内位移如图2 所示。

图2 CCSDDME 面内位移Fig.2 In-plane displacement of CCSDDME

2.1 结构的几何方程及本构关系

根据1 阶剪切变形理论和上述假设，结构的各层位移可表示为

由于层与层之间为理想黏接，无缝隙、无滑动，可知第2 层上表面和第3 层下表面的位移相同，第2 层下表面和第1 层上表面的位移相同。化简后得

同样可得第4 层中面位移为

结构第i层的位移‐应变关系表示为

每层的应力‐应变关系表示为

第i层的刚度矩阵表示为

通过坐标变换，可得到x⁃y坐标中的应力‐应变关系为

2.2 控制微分方程的推导

根据上面得到的应力‐应变关系式计算层合板的应变能和动能为

结构在边界x=0和x=a处的边界条件为0；vi=0；w=0=0；βi=0。其中i=1，3，5。

结构在边界y=0 和y=b处的边界条件为：=0；ui=0；w=0=0；αi=0。其中i=1，3，5。

应用Navier 型解法，满足四边简支边界条件的位移函数表达式为

其中：i=1，3，5；m和n为整数。

对于不同的m和n，结构将作不同波形的固有振动，也就有不同的固有频率。

利用Rayleigh‐Ritz 法可以得到共固化双层阻尼薄膜复合材料结构的控制方程，从而求解结构的各阶固有频率

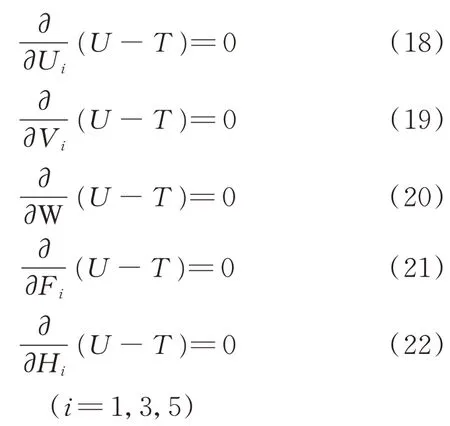
将位移表达式代入控制方程并简化成矩阵形式

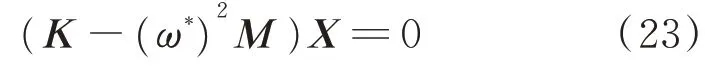
其中：M为质量矩阵；K为复刚度矩阵；X=(U1，U3，U5，V1，V3，V5，W，F1，F3，F5，H1，H3，H5)T

共固化双层阻尼薄膜复合材料结构的固有频率和损耗因子按式（24）进行计算

3 算例分析与讨论

为了检验推导公式的正确性，利用模态应变能有限元法分别计算双层阻尼薄膜嵌入的四边简支夹芯板的固有频率和损耗因子，其中损耗因子为无量纲参数。结构单元类型选为Solid185，单元尺寸取1 mm，材料参数分别如表1 和表2 所示。将模态应变能有限元法计算结果与Rayleigh‐Ritz 求解结果进行比较，如表3 和表4 所示

表1 弹性层材料参数Tab.1 Material parameters of composite layer

表2 黏弹性层材料参数Tab.2 Viscoelastic material parameters

表3 固有频率计算结果对比Tab.3 Comparison of natural frequency calculation results Hz

表4 损耗因子计算结果对比Tab.4 Comparison of loss factor calculation results

由表3 和表4 可知，由有限元计算出的固有频率和损耗因子与本研究算法计算的固有频率和损耗因子误差在5%以内。该理论所做的基本假定和有限元中单元格的大小都是造成误差的原因，但求解结果基本是吻合的，验证了该理论分析的正确性。

3.1 阻尼层位置对CCSDDME 固有频率和损耗因子的影响

保持结构总厚度不变，研究阻尼层位置对CCS‐DDME 固有频率和损耗因子的影响。为了便于表述，引入变量D，将其定义为两阻尼层中面间的距离，如图3 所示。D取不同值时，分别计算结构的固有频率和模态损耗因子，计算结果见图4 和图5。

图3 双层阻尼薄膜中面距离DFig.3 Mid-surface distance D of double-layer damping film

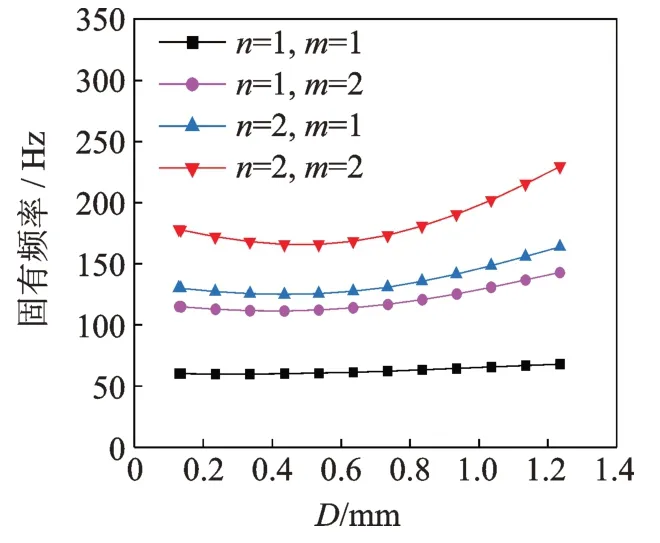
图4 固有频率随D 的变化规律Fig.4 Change law of natural frequency with the mid-sur‐face distance D

图5 损耗因子随D 的变化规律Fig.5 Change law of loss factor with the mid-surface dis‐tance D

由图4 可知，两阻尼层中面间的距离对1 阶固有频率影响较小，当D约为0.435 mm 时，结构的2 阶、3 阶和4 阶固有频率出现极小值。由图5 可知，结构损耗因子随着D的增大先增大后减小，存在设计最佳 值。当D值分别为0.435，0.535，0.535 和0.635 mm 时，结 构的1 阶、2 阶、3 阶和4 阶损耗因 子分别达到峰值。这是由于双层阻尼薄膜嵌入结构后，分别受到中间层和上下侧材料层的共同约束，随着D值的增加，阻尼层得到充分的受力变形，使CC‐SDDME 的模态损耗因子增大；而当D值继续增大，结构总厚度不变，结构上下层材料厚度减薄，使阻尼层的剪切应变减小，结构的损耗因子随之减小。

3.2 阻尼层剪切模量对CCSDDME 固有频率和损耗因子的影响

保持其他参数不变，研究阻尼层剪切模量对CCSDDME 阻尼性能的影响，分别计算不同的剪切模量下的固有频率和损耗因子，计算结果如图6 和图7 所示。

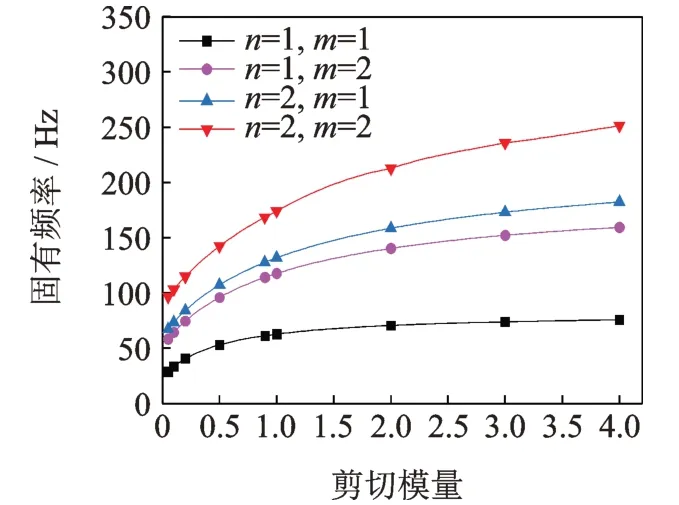
图6 固有频率随剪切模量的变化规律Fig.6 Change law of natural frequency with shear modulus

图7 损耗因子随剪切模量的变化规律Fig.7 Change law of loss factor with shear modulus

由图6 和图7 可知，随着结构剪切模量的增加，结构的整体刚度和固有频率随着增大。结构的损耗因子随着剪切模量的增大先增大后减小，存在设计的最佳值。当结构的剪切模量分别为0.2，0.5，0.5和0.896 MPa 时，结构的1 阶、2 阶、3 阶和4 阶损耗因子分别出现峰值。同时可以看出：剪切模量较高时，CCSDDME 高阶损耗因子高于低阶损耗因子；剪切模量较低时，CCSDDME 高阶模态损耗因子低于低阶损耗因子。

4 结论

1）将该理论计算的固有频率和损耗因子同有限元计算结果进行对比，验证了该理论的正确性。

2）结构固有频率随着两阻尼层中面距离的增大先减小后增大，存在极小值；结构损耗因子随着两阻尼层中面距离的增大先增大后减小，存在设计的最佳值。

3）随着结构剪切模量的增加，结构的固有频率随着增大。结构的损耗因子随着剪切模量的增大先增大后减小，存在极大值。当剪切模量较高时，高阶损耗因子高于低阶损耗因子；当剪切模量较低时，高阶模态损耗因子低于低阶损耗因子。