可移动着陆器腿足最优时间‐急动度轨迹规划∗

贾 山，周向华，张 胜，赵建华，陈金宝

（1.南京航空航天大学航天学院 南京，211106）（2.深空星表探测机构技术工信部重点实验室 南京，211106）（3.航天进入减速与着陆技术实验室 南京，211106）

引言

未来的人类深空星表探测将越来越频繁。在月球探测领域，中国探月工程在实现“绕、落、回”三步走之后，将继续进行“载人登月”和“月球基地建设”等任务。美国重启Artemis 登月计划，并以建立月球基地供人类长期驻留为最终目标［1］。在火星探测领域，中国、美国、阿联酋已于2020 年先后发射火星探测器，并将在2021 年到达火星开展后续探测活动。这些任务中，星表着陆是关键环节，决定了相关任务的成败。目前，着陆器均采取传统腿足式着陆缓冲装置与固定式着陆的组合，即着陆时姿态无法调整，着陆后位置无法移动，例如美国阿波罗计划、前苏联登月计划、中国探月工程等。这种组合与轮式巡视器相结合的方式存在着一定局限性：①被动式着陆缓冲不仅难以保证各着陆腿缓冲进程的统一，且对着陆点选择和着陆过程控制精度要求较为苛刻，同时难以在执行返回式任务时为上升器创造最佳的起飞姿态；②探测范围的可扩展性不足，传统着陆器搭载巡视器的探测方式受体积、能源以及通信等各方面的制约，可探测范围局限于着陆器周边的有限区域内，且往返式的探测路线存在较大的重复性；③对月面环境适应性较差，为保证着陆安全，着陆点要求尽可能位于地势较为平坦的区域，该区域基岩物质出露较少，勘探难度较大，很大程度上限制了任务的科学回报率；④对于载人探月及星表基地建设等任务适用性有限，在载人探月任务中，如果缓冲后的着陆姿态不是水平的，将会导致很多不便，且被动式的自平衡机构又会导致着陆器构型复杂，降低其着陆缓冲过程的安全性与可靠性，在星表基地建设任务中，传统着陆器无法承担物资转运、人员运输等工作。由此可见，兼具着陆缓冲和星表移动等功能的着陆器在未来深空星表探测领域有着重要的应用价值。

为此，笔者提出了一种可移动六足着陆器，通过在主/辅缓冲支柱中集成主动驱动功能的方式，实现了腿足式着陆缓冲机构的吸能/驱动一体化，可为未来开展多点位、大范围的星表探测提供一种切实可行的解决方案。为保证所设计可移动着陆器腿足机构运动过程的平稳可靠，需对其驱动关节的运动轨迹进行规划，并以时间‐急动度最优为目标进行相关轨迹的优化，从而使得各驱动关节具有平稳的运动过程和较短的行程时间。

在运动轨迹规划方面，Zhou 等［2］提出了一种着陆移动装置的最优时间‐急动度轨迹规划方法，并采用自适应遗传算法对轨迹进行了优化，得到了连续可靠的轨迹。Li 等［3］提出了一种高速摘放并联机器人的平滑轨迹规划方法，对操作空间轨迹进行了规划，但未对关节空间进行轨迹优化。Huang 等［4］研究了工业机器人的最优时间‐急动度轨迹规划方法，应用GSGA‐Ⅱ多目标优化函数对时间和急动度进行优化，但未分别考虑变量对时间、急动度的影响。Abu‐Dakka 等［5］提出了一种求解复杂环境下最优时间和无碰撞轨迹的方法，说明了除总行程时间的优化外，急动度的最小化对机械手的性能也有着十分重要的意义。Gasparetto 等［6］提出了一种不设置总时间情况下规划轨迹的方法，但该方法未对时间和急动度限定范围且未对时间‐急动度进行优化。丰意［7］对舱位对接机构的最优时间、急动度和能量进行了轨迹优化，采用人工免疫算法得到了三者最优解。陈栋等［8］提出一种并联机构运动学的多目标轨迹规划方法，以时间‐急动度为优化目标，并对每种轨迹方法下的调姿难度进行了分析，但未提出时间、急动度所占权重不同对优化值的影响。徐海黎等［9］采用罚函数的方法处理约束问题，对工业机器人的最优时间、能量进行了轨迹规划，并采用了人工免疫算法进行了最优解求解。徐扣［10］采用三次B 样条曲线对六自由度机械臂进行了轨迹规划。乔木［11］采用3 段修正正弦函数对码垛机器人进行了轨迹规划，并采用遗传算法对其时间变量进行了最优值求解。

在运动轨迹优化方面，遗传算法、免疫算法、退火算法以及多学科优化算法等智能算法［12］得到了广泛应用，其主要思想是将机器人关节或末端的轨迹方程转化为优化控制问题。其中，遗传算法有着全局收敛能力强、适应度函数易于构造等优势［13］。卢晓东［14］采用遗传算法对喷涂机器人进行了轨迹规划及优化。周锋［15］采用自适应遗传算法对工业机器人进行了轨迹规划。皮骏等［16］采用改进遗传算法对航空轴承的4 种故障工况进行了诊断。鄢波等［17］采用遗传算法对机器人末端位置补偿进行了轨迹规划。然而，传统遗传算法对高维、非线性和多峰问题的求解性不高，难以达到较高的求解精度和收敛速度。为此，林明等［18］提出了一种改进遗传算法改善了收敛速度和收敛精度。Pang 等［19］通过适当舍弃最优个体、改善交叉变异概率来改进遗传算法，对三肢机器人进行了最优轨迹规划。林阳等［20］采用多种群遗传算法对一般机械臂的逆运动学进行了求解。

笔者在上述所提出的可移动着陆器设计方案的基础上进行了以下工作：完成了运动学建模和落震缓冲性能分析；采用三次样条函数对其关节空间内各驱动位移轨迹进行规划；采用多种群遗传算法，并引入模拟退火思想改进交叉算子，引入移民算子、人工选择算子和精英保留策略提高算法收敛性和全局搜索能力；使用改进多种群遗传算法对各驱动进行了最优时间‐急动度轨迹优化；通过仿真试验验证了腿足各驱动关节的最优时间‐急动度轨迹的合理性和有效性。

1 可移动着陆器

1.1 可移动着陆器构型

笔者所提出的可移动着陆器由1 个正六棱台本体和6 条三自由度腿足机构组成。每条腿足机构均由1 个主支柱和2 个辅助支柱构成，主支柱和辅助支柱内置缓冲/驱动一体化装置，该装置由驱动电机、滚珠丝杠和缓冲材料组成，可实现着陆器的缓冲吸能和星表移动。图1 为缓冲/行走一体化着陆器整机构型示意图。

图1 可移动着陆器构型Fig.1 Buffering/walking integrated hexapod lander

1.2 可移动着陆器运动学模型

以着陆器腿足与本体连接点O0为原点，建立腿足坐标系如图2 所示。在该连接点处建立基坐标系{O0}，以该点处胡克铰为转动关节建立坐标系{O1}和{O2}。O3为主缓冲支柱与足垫连接点，以该点处球铰建立足端坐标系{O3}。坐标系{O1}和{O2}处的关节转角为θ1和θ2；{O3}处的关节伸缩位移为p1；L1为主支柱初始长度；L2和L3为辅助支柱初始长度。由改进D‐H 参数法建立单腿机构连杆参数表，如表1 所示。

表1 着陆器单腿机构连杆参数表Tab.1 Link parameters of single leg

图2 着陆器单腿关节坐标系示意图Fig.2 Joint coordinates of lander single leg

其中

其中：r11～r33用于描述足端坐标系{O3}在坐标系{O0}下的姿态；px，py，pz用于描述足端坐标系{O3}在坐标系{O0}下的位置。

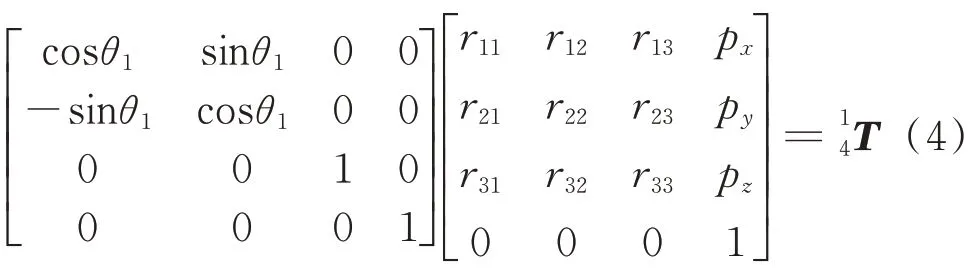
令方程两边的元素（1，4）（2，4）（3，4）相等，可得到方程组为

对方程组求解可得运动学逆解为

在坐标系{O0}下，U1和U2的位置坐标固定，S1和S2的位置坐标可由运动学正解求得。图2 所示关节转角θ1和θ2发生转动后，根据U1，U2，S1和S2在坐标系{O0}下的位置坐标，可求得2 组辅助支柱的关节伸缩变化量与关节转角θ1，θ2之间的变换关系为

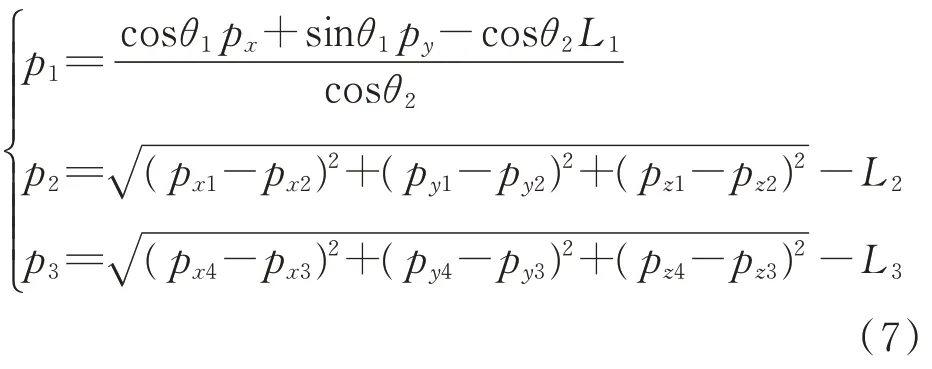
其 中：(px2，py2，pz2)和(px3，py3，pz3)为S1和S2在坐标系{O0}下的位置坐标；(px1，py1，pz1)和(px4，py4，pz4)为U1和U2在坐标系{O0}下的位置坐标。

1.3 可移动着陆器缓冲性能

可移动着陆器的构型参数和性能指标如表2 所示，通过多体动力学仿真软件ADAMS 对着陆器缓冲性能进行仿真分析。设定重力加速度为月球重力加速度（1.63 m/s2）；设定足端与月面接触动静摩擦因数均为0.45，该系数满足月壤摩擦力要求。对着陆器进行了3 种工况的仿真，分别是坡度为0°的垂直着陆（工况1）、坡度为8°的“2‐2‐2”着陆（工况2）和坡度为8°的“1‐2‐2‐1”着陆（工况3），各工况下足端触地速度均为1.5 m/s。测得本体质心处过载加速度曲线如图3 所示，3 种工况下缓冲过程如图4 所示。由图3 可知，3 种工况下本体质心处最大过载均满足要求，具备良好的缓冲性能。

表2 可移动着陆器构型参数和性能指标Tab.2 Mechanism parameters and performance in‐dexes

图3 3 种工况过载加速度曲线Fig.3 Three conditions of overloading acceleration-time curve

图4 3 种工况下着陆器缓冲示意图Fig.4 Three conditions of lander buffering

2 最优时间‐急动度轨迹问题描述

轨迹规划过程可以同时在任务空间和关节空间内实现，图5 描述了任务空间和关节空间内轨迹规划的关系。关节空间内进行轨迹规划时，首先在任务空间内对任务轨迹插补得到关键点，再根据逆运动学将各关键点转换为关节空间内对应关节点的矢量值，最后将关节点根据任务要求拟合成光滑函数曲线。关节空间内轨迹规划无需描述任务空间内关键点的姿态问题，且不存在结构的奇异问题，因此操作方便。关节空间与任务空间的映射关系是非线性的，关节空间内的轨迹规划过程不能直接反应出任务空间内腿足末端的执行轨迹。本研究所述可移动着陆器对移动速度、足端位置精确度要求不高，但对系统的抗振动、抗冲击能力要求较高，故在关节空间内进行轨迹规划，以减小驱动部件在工作过程中的振动和冲击。

图5 任务空间与关节空间轨迹规划关系图Fig.5 The relationship between task space and joint space in trajectory planning

2.1 轨迹生成

关节空间内的轨迹可由关节空间内的一系列节点组成，采用三次样条曲线来连接这些节点，可以获得每个节点处的位移、速度、加速度和急动度。对于关节i(i=1～N)，设q1，q2，…，qj，…，qn为其关节空间内的节点；t1，t2，…，tj，…，tn为与之相对应的时刻。定义Sij(t)为时间间隔[tj，tj+1]内的三次多项式函数，和分别为节点qj，qj+1 之间的位移、速度、加速度和急动度。各关节初始时刻和终止时刻的速度值与加速度值均已知。根据三次样条曲线定义，其Lagrange 形式的表达式为

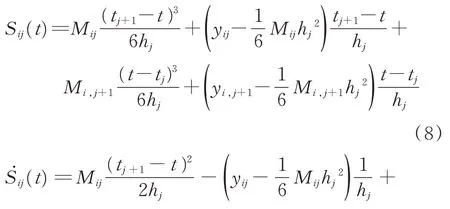
其中：Sij(t)为关节i在时间间隔[tj，tj+1］内的位移；为关节i在时间间隔[tj，tj+1]内的速度为关节i在时间间隔[tj，tj+1]内的加速度为关节i在 时间间隔[tj，tj+1]内的急动度；yij为关节i在时间间隔[tj，tj+1]内第j个插值节点的位移；hj为tj与tj+1之间的时间间隔；tj为时刻点；i=1，2，…，N，表示有N个关节点；j=0，1，…，n，表示有n+1 个插值点。

2.2 约束条件

可移动着陆器腿足共有3 个约束，分别为速度约束、加速度约束和急动度约束，表明其动态行为需在正确控制下合理应用，从而限制可移动着陆器的过度损耗。

速度约束

加速度约束

急动度约束

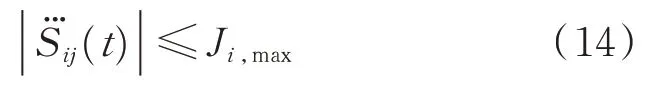
其中：Vi，max，Ai，max和Ji，max分别为关节i的速度、加速度和急动度的约束；i=1，2，…，N；j=0，1，…，n。

2.3 目标函数

由式（11）可以看出，腿足在运动过程中各关节存在冲击（急动度）且不连续。因此，为减小冲击对腿足运动稳定性和各零部件工作寿命的影响，建立了最优时间‐急动度轨迹规划模型，目标函数为

因为急动度存在正负值，故对其取绝对值，其余各符号定义与上述一致。

3 轨迹优化——多种群遗传算法

3.1 单种群遗传算法描述

单种群遗传算法是一种模拟自然选择进化过程的智能算法。相比于其他智能算法，遗传算法避免了复杂的数学推导和参数选择，有着很强的全局寻优能力和鲁棒性。单种群遗传算法在变量数目增加时，计算量增大，寻优能力下降，忽视了算法可并行运算的潜力，难以实现全局最优解的搜索。

3.2 多种群遗传算法描述

在最优时间‐急动度轨迹规划中，要想获得平滑的轨迹曲线，势必会引入较多的插值点，导致优化变量随之增加。然而，传统单种群遗传算法对多目标、非线性和多峰问题的求解能力不足，随着优化目标的增加，算法的收敛速度和收敛精度会下降，易陷入局部最优解。多种群并行遗传算法是一种改进的遗传算法，近年来被广泛运用于解决多目标最优值等问题。在最优多种群并行计算过程中，其局部收敛和收敛速度慢等问题没有得到明显改善。为此，笔者从以下方面进行改进：

1）采用多种群遗传算法，引入多个种群同时进行优化搜索，对不同种群赋予不同控制参数，实现不同的搜索目的；

2）引入模拟退火算法思想改进交叉概率，使算法运行后期种群个体趋于最优值时，以小变化搜索最优值，避免造成局部收敛或无法收敛等情况；

3）采用移民算子对各种群并行计算进行调节，使最优解为各种群协同进化的结果；

4）通过精英种群保留策略保存各种群每个进化代中的最优个体，并实时更新最优个体种群，采用人工选择算子保存各种群进化中最优个体，并作为算法收敛与否的依据。

图6（a）为单种群遗传算法流程图，图6（b）为多种群遗传算法流程图。其中：G为当前运行的代数；XN为每个群体中的个体数；XM为种群数目；GMAX为最大进化代数；Fitness(F(G，N)，XN)为适应度函数；F(G，N)为运行到第G代的第N个种群。本研究采用多种群遗传算法并在上述4 个方面进行改善，对最优时间‐急动度轨迹规划模型进行了最优值求解。

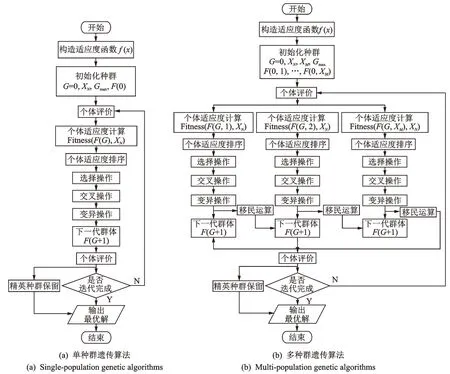
图6 遗传算法流程图Fig.6 Genetic algorithm

3.3 轨迹优化求解算法

在多种群遗传算法基础上，对变量采用二进制编码，将目标函数分解为时间函数和急动度函数组成的方程组，构建最大值求解的适应度函数，并引入权值因子改变时间、急动度所占权重大小和平衡搜索速率，采用多点交叉的交叉算子并引入模拟退火思想改进交叉概率，引入移民算子进行协同进化，对精英种群进行保留。

基于多种群遗传算法的最优值求解分为8 个步骤，具体描述如下。

1）构造目标函数。将最优时间‐急动度轨迹规划模型的目标函数分解为式（16）所示非线性方程组其中：根据先验条件设定变量的边界范围为hj，min≤hj≤hj，max。

2）初始化种群。初始设置种群数目为XM，各种群个体数目为XN，个体均采用二进制编码。单个种群采用二维矩阵来存储数据集合。交叉概率Pc和变异概率Pm用来均衡算法的全局搜索和局部搜索能力，交叉算子是新个体产生的主要算子，变异算子用于提升算法的全局搜索能力。其中，初始设置交叉概率Pc为0.8，初始变异概率Pm为0.01。

3）设计适应度函数。遗传算法在进化搜索过程中仅以适应度函数为依据，且其目标函数不受连续可微约束，定义域可为任意集合。由于目标函数为非线性方程组，故将其映射成适应度函数

其中：α为时间权值系数，用于改变时间、急动度所占权重的大小，0 ≤α≤1；β为数量级权值系数，计算可知时间的数量级为100，急动度的数量级为102，故取β=0.01 来平衡搜索速率。

4）确定选择策略。采用“轮盘赌”选择法，利用各个体适应度所占比例大小来决定其子代保留的可能性。

5）确定交叉算子。单点交叉算子只能提取部分基因信息，这将限制算法搜索能力。笔者采用多点交叉的方式，多点交叉是指父母染色体中在两个相连的交叉位间的基因进行交换，产生两个新的子代。多点交叉可以促进算法进行稳定、高效地搜索，避免早熟现象发生。

在标准遗传算法中，由于交叉概率确定，导致任意一个基因位作为交叉位置的概率是相等的，但等概率地选取交叉位置并不能有效地搜索最优解。由于个体采用二进制编码，不同基因位的改变造成个体适应度值的改变程度不同，因此等概率地选取交叉位置必将影响遗传算法的寻优能力，笔者引入模拟退火思想对交叉概率进行改进。对于第G代种群，设每个个体的第i个基因位的交叉概率为保留算法运行过程中产生的当前最优解X(q)*。在每一代运行中，对于在第i个基因位做多点交叉可以得到两个子代X2和Y2，则基于模拟退火算法思想，交叉算子修改公式为

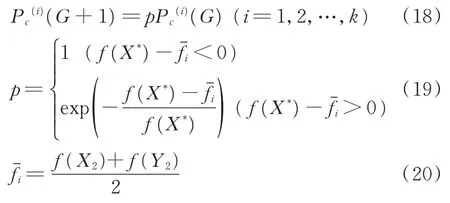
其中：k为染色体长度；X*为当前最优解。

由此可见，交叉概率是自适应变化的。

6）采用移民算子进行协同进化。在进化过程中，采用移民算子在各种群之间建立信息交流，定期将相邻种群的最优个体与最差个体进行互换，具体替换流程如图7 所示。采用移民算子可使各种群之间保持协同进化，从而提高整体收敛速度与精度。

图7 移民运算替换流程Fig.7 Immigration operator

7）对精英种群进行保留。在进化的每一代，采用人工选择算子将适应度值高的种群保留至精英种群，精英种群不再进行选择、交叉及变异等操作，只进行更新，以保证最优个体不被破坏和丢失。

8）进化结束，输出最优解

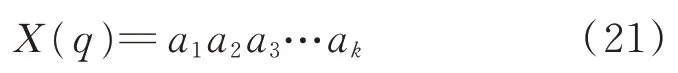
其中：X(q)为具有最优适应度值的个体，a1a2a3…ak为其编码值，将a1a2a3…ak替换为实数即可得到最优解。

4 仿真分析

以可移动着陆器单腿机构为例，足端步长s与步高h已知，足端圆锥抛物曲线轨迹和方程分别如图8 和式（22）所示

图8 足端迈步轨迹图Fig.8 Foot trajectory planning

根据表2 所述构型参数和任务要求，设定该着陆器足端步长为300 mm，步高为200 mm。对足端迈步轨迹进行关键点均匀采样，可得各节点在坐标系{O0}下的坐标。然后，由可移动着陆器单腿逆运动学，可求得足端轨迹在各关节空间中的驱动关节位移量，如表3 所示。由于关节初始速度、初始加速度、最终速度和最终加速度为定值，故在其初始时间间隔和最终时间间隔内插入虚拟节点来保证其速度与加速度的连续［21］。

表3 足端迈步轨迹及关节空间节点Tab.3 Foot trajectory and joint space nodes

关节空间内驱动关节位移量已知后，由三次样条曲线拟合各节点，可得到关节空间内驱动轨迹。基于最优时间‐急动度模型，在Matlab 下进行了对比试验，分别采用单种群遗传算法和多种群改进遗传算法对轨迹进行优化，对比两种算法和收敛精度，进一步说明多种群遗传算法的优势。

参数设置如下。

1）多种群遗传算法：个体数目XN=200，个体染色体长度k=20，种群规模XM=20，迭代次数Gmax=200，初始交叉概率Pc=0.8，初始变异概率Pm=0.01，下边界hj,min=[1 0.5 0.5 0.5 0.5 0.5 0.5 1]，上边界hj,max=[2 1 1 1 1 1 1 2]，采用模拟退火算法改进交叉算子，采用移民算子促进种群协同进化。其中，可移动着陆器腿足机构各关节速度、加速度和急动度约束条件如表4 所示。基于多种群改进遗传算法，参数设置同上，通过修改适应度函数内时间权重系数α的值，可得到时间权重系数与时间和急动度的关系如图9 所示。由图可以看出，当时间权重增大时，总时间逐步减小，急动度值逐步增大，时间的最大值为29.223 0 s，最小值为15 s；急动度的最大值为5 180.484 0 mm/s3，最小值为591.205 5 mm/s3。

表4 可移动着陆器腿足各关节约束Tab.4 Joint limitation of leg‐foot

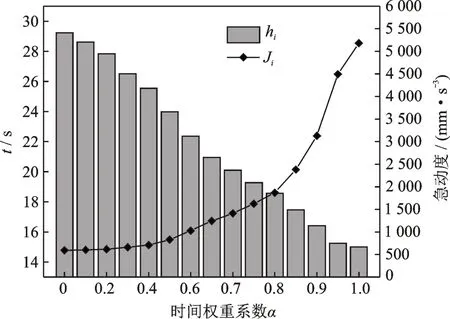
图9 时间权重系数影响曲线Fig.9 Influence curve of time weight coefficient

由于可移动着陆器对行走速度要求不高，故笔者选取较小的时间权重系数（α=0.4）来使着陆器驱动部分具有更低的急动度。

2）单种群遗传算法：个体数目XN=200，个体染色体长度k=20，迭代次数Gmax=200，交叉概率Pc=0.8，变异概率Pm=0.01，上边界hj,min=[1 0.5 0.5 0.5 0.5 0.5 0.5 1]，下边界hj,max=[2 1 1 1 1 1 1 2]。

将该时间权重系数（α=0.4）代入适应度函数中，分别采用单种群遗传算法和多种群改进遗传算法优化5 次，记录最优结果和最差结果的最佳变量值和目标函数值，如表5 所示。

表5 两种遗传算法优化结果Tab.5 Optimization results of two genetic algorithms

由于采取数量级权值系数来平衡搜索速率，目标函数值相差不大，但可以看出急动度存在较大差异。将多种群遗传算法最优解的最佳变量值［1.993 8 0.805 6 0.779 0 0.711 1 0.780 8 0.789 2 0.817 9 1.995 3］代入式（8）～（11），可得关节空间内时间‐位移曲线、时间‐速度曲线、时间‐加速度曲线和时间‐急动度曲线，如图10 所示。

图10 各关节位移、速度、加速度和急动度变化曲线Fig.10 Time-displacement,time-velocity,time-accelera‐tion,time-jerk curve of joints

由图10（a）可知，关节1 的位移曲线光滑平缓，速度和加速度均未发生突变，速度峰值未超过100 mm/s，加速度峰值未超过100 mm/s2，腿足机构具有良好的运动性能，急动度存在突变，但其峰值未超过100 mm/s3，即腿足机构主缓冲支柱在运动过程中不会产生较大的冲击抖动。由图10（b，c）可知，关节2 和关节3 由于呈对称分布，其各曲线均相同，位移曲线光滑平缓，速度和加速度未发生突变，速度峰值未超过25 mm/s，加速度峰值未超过20 mm/s2，急动度峰值未超过35 mm/s3，即腿足机构辅助缓冲支柱在运动过程中具有良好的运动特性。

5 结论

1）采用三次样条曲线构造关节空间轨迹时，引入2 个虚拟节点，保证了速度曲线和加速度曲线的连续性。

2）对多种群遗传算法进行了改进，引入模拟退火算法思想改进交叉算子，引入移民算子保证各种群协同进化，引入人工选择算子保留精英种群，提高了算法全局搜索能力和最优解收敛性。

3）以总时间和总急动度为优化目标，采用多种群遗传算法对关节空间轨迹进行优化，给出了时间权重系数对总时间和总急动度的影响曲线。

4）选取合适的时间权重系数，权衡了时间和急动度对腿足机构运动性能的影响，实现了可移动着陆器腿足机构的最优时间‐急动度的轨迹规划。