基于流体流动参数检测的过滤器滤网分析∗

俞瑞利，梁 瑞，周文海，岳守体，崔本廷，陈 斐，杨 曦

（1.兰州理工大学石油化工学院 兰州，730050）（2.太原卫星发射中心 太原，030027）

引言

航天发射试验是一项高科技、高投入、高风险的任务，供气系统作为发射场地面设备的重要组成部分，其良好的稳定性、可靠性是确保试验任务成功的重要保障。管道中的粉尘等固体杂质颗粒随气流运动会磨损压缩机、管道和仪表等，导致其损伤、破坏，影响输气正常运行，故必须严格控制多余物和检查洁净度。一般在泵、压缩机等设备入口的管道上设置安装过滤器来过滤固体杂质，以保证设备能正常运转。国内外对过滤器流场的数值模拟大多结合内部结构复杂的多孔介质模型，采用Darcy 模型以及该模型的改进形式［1‐3］。该模型无需对流体和固体区域进行区分，采用体积平均法处理方程，而对于温度场的计算，大多采用局部不平衡模型［4‐5］。利用有限元和试验等方法对同种滤料不同结构参数的过滤特性进行模拟，对常见天然气管道过滤器的性能［6］、不同喷嘴的结构形式对出口流场的压力影响［7］、气液分离性能［8］以及褶式滤芯过滤器进行了大量研究［9‐15］。对于过滤器滤网的研究，大多是对圆柱形金属丝网滤芯结合现有的研究方法与技术进行数值模拟［16‐17］，通过与试验数据的对比，证明图示化模型的可行性，而不必用真实的几 何模型 进行计算［18‐19］。在气体过滤过程中，微流体对滤网的冲击［20］同样也会影响过滤性能。

管道过滤器作为重要的管路部件，其安全可靠性对地面供气系统有非常重要的影响，而过滤器滤网又是重中之重。滤网在流体流动过程中，瞬间的不稳定流动会引起较大的变形，甚至发生局部网丝断裂的破坏现象，使得过滤器失效。滤网的变形量可用滤网应变来表征，故笔者对影响滤网应变的流体参数进行分析。利用无量纲π理论，得到在含有固体杂质颗粒的气体流动过程中影响过滤器滤网应变的表达式。利用Fluent 有限元分析软件，通过改变流体的物理参数以及流动参数，得到滤网应变与流体物理参数、流动参数的关系，并与利用无量纲π理论所得公式进行比较，所得规律较吻合。在实际工程中，可通过检测流体的流动参数来保护过滤器滤网，使其持续高效地进行过滤操作。

1 无量纲理论

1.1 无量纲化气相流体对滤网应变的影响模型

含有固体杂质的气体过滤过程中，流体流动阻力会引起滤网变形。将引起滤网应变的气相流体的相关物理量总结为6 个［21］，如表1 所示。

表1 引起滤网应变变化的气相流体相关物理量Tab.1 Gas‐phase fluid‐related physical quantities affecting the strain acting on the filter screen

依据量纲分析π定理，取ρg，ug和d为独立量纲，将影响滤网应变的函数模型用7 个独立参量组合成的4 个无因次组数πi之间的函数关系来表示

因此，流体流动对滤网应变影响的函数关系式可表示为

由无量纲理论可知，不同无因次量π的乘积和商比仍为无因次量，取π1进行计算，解得

整理得

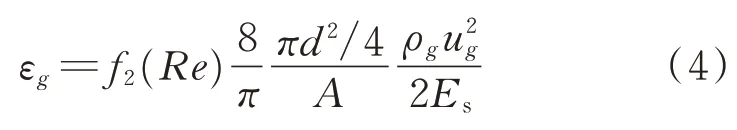
其中：无量纲项f2(Re)为阻力系数，用λg表 示；为流通区域的面积，用S表示。

故流体对滤网应变的影响可表示为

1.2 无量纲化固相流体对滤网应变的影响模型

含有固体杂质的气体过滤过程中，流体流动阻力会引起滤网变形。将引起滤网应变的固相流体相关物理量总结为以下7 个［21］，如表2 所示。

表2 引起滤网应变变化的固体杂质相关物理量Tab.2 Physical quantities related to solid impurities affecting the strain acting on the filter screen

依据量纲分析π定理，取μp，up和Es为独立量纲，将影响滤网应变的函数模型用8 个独立参量组合成的5 个无因次组数πi之间的函数关系来表示

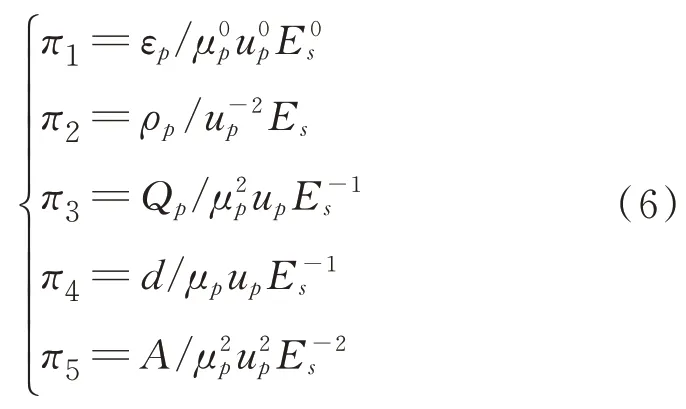
因此，固体杂质流动对滤网应变影响的函数关系式可表示为

由无量纲理论可知，不同无因次量π的乘积和商比仍为无因次量，取π1进行计算，解得

故固体杂质颗粒对滤网应变的影响可表示为

1.3 滤网应变

通过无量纲分析，分别得到了气相流体对滤网应变影响的计算公式以及固相流体对滤网应变影响的计算公式。假设流体速度与固体杂质颗粒的速度相等（u=ug=up），忽略流体与固体颗粒之间的相互作用，根据流体流动阻力引起的滤网变形，将含有固体杂质的流体流动冲击对过滤器滤网应变的计算公式简写为气相流体流动对滤网产生的应变与固体杂质颗粒流动对滤网产生的应变之和

由式（11）可知，在含有固体杂质颗粒的流动中，当流体流动区域面积和滤网有效阻拦面积一定，可得：

1）滤网的应变与流体流动速度呈二次函数关系；

2）滤网的应变与所含固体杂质颗粒的质量流量呈一次函数关系；

3）滤网的应变与气相流体的物理性质有关；

4）滤网的应变随滤网材料弹性模量的增大而减小。

2 模型的建立

2.1 物理模型

管道过滤器滤芯一般为圆柱形，但其有限元模型难以表征。基于滤网的结构特点，若将过滤网结构的每根钢丝都建立出来，所得的有限元模型较为复杂，故笔者将过滤网结构抽象为没有刚度的刚单元，来表征过滤网结构的宏观力学性能。将滤芯简化为平面型，再将丝网垫简化为等厚度的圆形丝网垫，进而变为相互平行的丝网［22］，并建立长度为5 mm 的流体流道进行模拟分析，如图1 所示。

图1 有限元模型Fig.1 Finite element model

2.2 网格划分

不同的网格划分方法会引起最终计算结果的差异，为使计算可较好地收敛且网格疏密程度对计算结果的影响较小，需要选取较适合本次模拟的网格进行计算分析［23］。

笔者通过建立4 种不同的疏密网格模型进行试计算，在气相流体介质为空气（Air）、入口流速均为10 m/s、固相颗粒物的质量流量为0.05 kg/s、颗粒直径为1 mm、滤网材料的密度为7 850 kg/m3、弹性模量为2×1011Pa 及泊松比为0.35 的情况下，对比分析其滤网应变，如表3 所示。

表3 不同网格划分下滤网应变的变化Tab.3 Strain acting on the filter screen for different meshes

网格越密，数值模拟得到的计算结果越准确，但对计算机要求较高，且计算时间较久。以第4 种最密网格为参考，对比滤网应变，其结果表明：

1）第1 种较疏网格在计算过程中残差较大，相比第4 种较密网格，所得的滤网最大应变相差约38.7%；

2）第2、第3 种网格划分方式是对滤网网格进行加密处理，与第4 种较密网格相比，得到的滤网应变计算结果相差4.8%和1.9%。

综合考虑计算准确度、计算时间及迭代残差，本研究网格模型的网格总数为142 154，对滤网网格进行加密处理，占网格总数的15.1%，如图2 所示。

图2 网格划分Fig.2 Meshing

2.3 边界条件

边界条件如下：

1）3 种气相流体的入口均设置为速度入口，出口设置为自由出口，为对比流体在不同入口速度下对滤网应变的影响，保证其他入射条件相同，且不同的速度入口条件下均为独立算例；

2）其余各面均设置为无滑移绝热壁面，固体颗粒与流场内壁发生碰撞后被收集，不考虑反弹作用；

3）采用离散相（discrete phase model，简称DPM）模型定义杂质颗粒的属性，假设颗粒为惰性球形，密度为2 046 kg/m3。

2.4 控制方程

在Fluent‐DPM 模型中，流体主相视为连续相，次相固体颗粒视为离散相，各项的物理性质保持不变。

2.4.1 连续相连续性方程及动量方程

连续性方程即质量守恒方程，流体流动的连续性方程和动量方程［24］可表示为

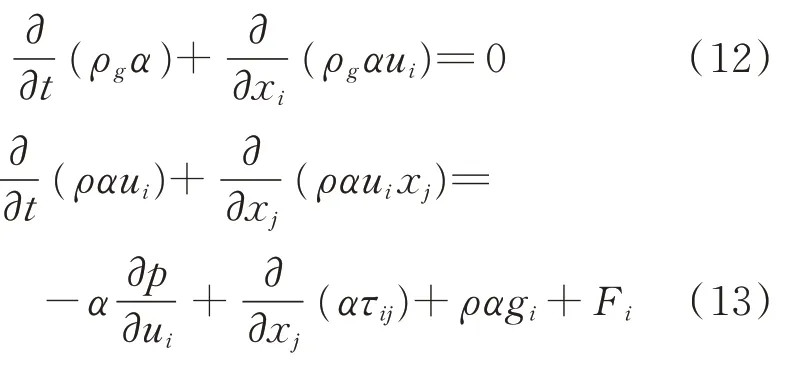
其中：α为连续流体的体积率；ρg为流体相密度；p为静压；ui为流体相在笛卡尔坐标i方向上的流速分量；gi为坐标i方向上的体积力；τij为黏性应力张量；Fi为连续相与离散相的相互作用力。

2.4.2 离散相运动方程

颗粒作用力平衡方程在笛卡尔坐标系下的形式［25］为

其中：ug为连续相在x方向的速度；ρp为离散相颗粒在x方向的密度；uP为离散相颗粒速度；FD为颗粒的单位质量阻力；Fx为x方向的其他作用力。

颗粒的单位质量阻力FD表达式为

其中：CD为阻力系数；μg为连续相动力黏度；dp为离散相颗粒粒径；Re为雷诺数。

2.4.3k‐ε湍流模型

考虑到管道内多相流介质的混合效果，气固相存在自由流状态，故选择Realizablek‐ε湍流模型对动量模型方程进行封闭求解。湍动能及其耗散率运输方程［26］为

其中：k为湍动能；ε为耗散率；μi为i方向的速度分量；xi，xj分别为i和j方向上的坐标分量；μt为湍流黏度；GK为速度引起的湍动能生成项；Gb为浮力引起的湍动能生成项；YM为可压缩湍流脉动膨胀对总的耗散率影响；αk，αε分别为湍动能及其耗散率的湍流普朗特数；C1ε，C2ε，C3ε为常数。

当浮力应力层中速度方向与重力方向相同时，C3ε的值为1；当浮力应力层中速度方向与重力方向垂直时，C3ε的值为0。

2.4.4 流固耦合

流固耦合基于牛顿第三定律。在一个流动过程中，颗粒对流体的作用力与流体对颗粒的作用力存在差异。为减小差异，采用式（19）计算空隙率［27］

其中：ε2d为二维系统空隙率。

颗粒对流体的作用力为

其中：ϖ为修正因子；B为权函数；εi为气体空隙率；Δt为时间步长；ei为i方向的离散速度。

流体对颗粒施加的作用力为

其中：μg为流体黏度；VP为颗粒体积；C，d为有效曳力系数，且

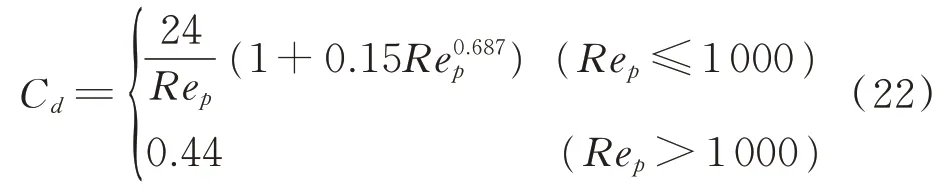
颗粒Reynolds 数为

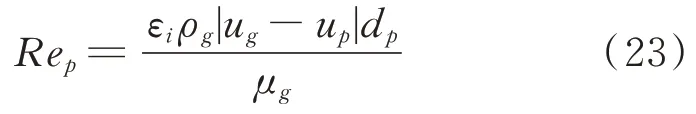
在流固耦合交界面处，滤网的动力学方程［28］可以由牛顿第二定律导出

其中：ρs为滤网的密度；as为滤网的速度矢量；τs为滤网应力；σs为滤网的柯西应力张量；Fs为滤网的体积力矢量。

2.5 基本假设

针对本研究模拟，做出如下假设：

1）流动过程中，所建几何模型不发生形变；

2）由于颗粒较小，质量流量较小，故不考虑重力；

3）因入口距滤网较近，假设流体入口速度等于流体接触滤网的速度；

4）入口气相流体的速度等于固相流体的速度。

3 分析与讨论

3.1 不同流体速度对滤网应变的影响

当气相流体为空气，固体杂质颗粒的直径为1 mm，质量流量为0.05 kg/s，滤网材料的密度为7 850 kg/m3，弹性模量为2×1011Pa，泊松比为0.35，在不同的流体速度冲击下，滤网的应变云图如图3 所示。

图3 不同流体速度下的滤网应变Fig.3 Filter screen strain at different fluid velocities

当气相流体分别为空气（Air）、甲烷（CH4）和氮气（N2）时，在相同的固体杂质颗粒参数（颗粒直径为1 mm、质量流量为0.05 kg/s）和相同的滤网材料（密度为7 850 kg/m3、弹性模量为2×1011Pa、泊松比为0.35）下，滤网的最大应变分别如图4～6 所示，滤网的最大变形量随流体入口速度的变化情况分别如图7～9 所示。

图4 滤网最大应变随空气入口速的变化情况Fig.4 The maximum strain of the filter screen changes with the fluid inlet velocity of air

通过比较图4 与图7、图5 与图8、图6 与图9 可以看出，滤网的应变与最大变形量有相同的规律。当气相流体为空气（Air）、甲烷（CH4）和氮气（N2）、固体杂质颗粒的颗粒直径为1 mm、质量流量为0.05 kg/s、滤网材料的密度为7 850 kg/m3、弹性模量为2×1011Pa、泊松比为0.35 时，流通面的面积不变，滤网的有效阻拦面积不变，只改变流体的流动速度，通过拟合，得到滤网最大应变关于流体入口速度的函数表达式如下。

图5 滤网最大应变随甲烷入口速度的变化情况Fig.5 The maximum strain of the filter screen changes with the fluid inlet velocity of methane

图6 滤网最大应变随氮气入口速度的变化情况Fig.6 The maximum strain of the filter screen changes with the fluid inlet velocity of nitrogen

图8 滤网最大变形量随甲烷入口速度的变化情况Fig.8 The maximum deformation of the filter screen changes with the fluid inlet velocity of methane

图9 滤网最大变形量随氮气入口速度的变化情况Fig.9 The maximum deformation of the filter screen changes with the fluid inlet velocity of nitrogen

空气（Air）

y=0.004 2x2+0.044 7x（R2=0.999 5）

甲烷（CH4）

y=0.002 3x2+0.026 4x（R2=0.999 9）

氮气（N2）

y=0.003 9x2+0.038 6x（R²=0.999 9）

由拟合的公式可以看出，无论何种气相流体，通过改变流体的入口速度，得到滤网最大应变与流体流动速度呈二次函数关系，而且拟合度较高。此结论与利用无量纲π定理推导得出的关于滤网最大应变与流体流动速度的量级一致。

3.2 不同固体杂质颗粒质量流量对滤网应变的影响

当流体的入口速度保持10 m/s 不变，固体杂质颗粒的颗粒直径不变，滤网材料（密度为7 850 kg/m3、弹性模量为2×1011Pa、泊松比为0.35）不变，气相流体分别为空气（Air）、甲烷（CH4）和氮气（N2）时，滤网最大应变随固体杂质颗粒质量流量的变化趋势分别如图10～12 所示。

图10 空气中杂质颗粒的质量流量对滤网最大应变的影响Fig.10 The influence of the mass flow of impurity particles in the air on the maximum strain of the filter

图11 甲烷中杂质颗粒的质量流量对滤网最大应变的影响Fig.11 The influence of the mass flow of impurity particles in the methane on the maximum strain of the filter

当气相流体为空气（Air）、甲烷（CH4）和氮气（N2）、流体的入口速度为10 m/s、固体杂质颗粒的颗粒直径为1 mm、滤网材料的密度为7 850 kg/m3、弹性模量为2×1011Pa、泊松比为0.35 时，流通面的面积不变，滤网的有效阻拦面积不变，只改变固体杂质颗粒的质量流量。通过拟合，得到滤网最大应变关于固体杂质颗粒质量流量的函数表达式如下。

空气（Air）

y=0.114x+0.965（R²=0.963 6）

图12 氮气中杂质颗粒的质量流量对滤网最大应变的影响Fig.12 The influence of the mass flow of impurity particles in the nitrogen on the maximum strain of the filter

甲烷（CH4）

y=0.071x+0.561 7（R²=0.907 6）

氮气（N2）

y=0.167 2x+0.891 6（R²=0.957 3）

由拟合的公式可知，无论何种气相流体，在速度等参数不变时，只改变固体杂质颗粒的质量流量，得到滤网最大应变与固体杂质颗粒的质量流量呈一次函数关系，且拟合度较好。这种规律与利用无量纲π定理推导得出的关于滤网最大应变与固体杂质颗粒质量流量的量级一致。

3.3 在相同流动下不同气相流体对滤网应变的影响

为探究不同的气相流体在相同流动情况和相同滤网材料下滤网应变的变化情况，对比了不同气相流体的物理参数，具体数据如表4 所示。

表4 不同气相流体的物理参数Tab.4 Physical parameters of different gas‐phase fluids

由表4 可知，3 种气相流体的物理参数各不相同。其中：密度为Air>N2>CH4；比热为N2>CH4>Air；导热系数为CH4>Air=N2；黏度为Air>N2>CH4；偏心因子为N2>Air>CH4。

对比3 种不同的气相流体在相同的流动条件、不同的入口速度（20，40，60，80，100 m/s）下滤网的最大应变，如图13 所示。

图13 不同气相流体对滤网最大应变的对比图Fig.13 Comparison of the maximum strain acting on the fil‐ter screen for different gas-phase fluids

由图13 可知，当流动参数、滤网参数保持不变，在相同的流体入口速度下，滤网最大应变为Air＞N2＞CH4。由表4 可知，气相流体的密度和黏度也是相同的规律，但影响流动的气相流体的物理参数较多，无法确定影响因素仅仅是密度和黏度。综上可知，在流动参数、滤网参数不变的情况下，不同的气相流体对滤网的应变有不同的影响。

3.4 在相同流动下不同滤网材料参数对滤网应变的影响

为探究不同的滤网材料在相同流动情况下滤网应变的变化情况，对比了不同滤网材料的物理参数，如表5 所示。

表5 不同滤网材料的物理参数Tab.5 Physical parameters of materials of different filter screen

由表5 可知，3 种滤网材料的物理参数各不相同。其中：密度为B>A>C；弹性模量为A>C>B；泊松比为B>A>C。

气相流体介质为空气，对比3 种不同的滤网材料在相同的流动条件、不同的入口速度（20，40，60，80，100 m/s）下滤网的最大应变，如图14 所示。

由图14 可知，当流动参数不变，同一种气相流体在相同的流体入口速度下，滤网最大应变为B>C>A。由表5 可知，滤网材料的弹性模量是相反的规律。由此可得，滤网的应变随滤网的弹性模量的增大而减小，此结论与利用无量纲π定理推导得出的公式中体现的规律一致。

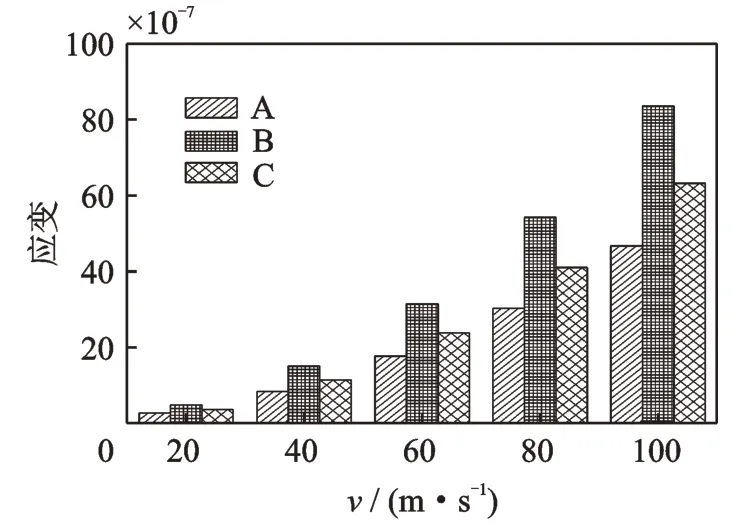
图14 不同滤网材料下滤网最大应变对比图Fig.14 Comparison of the maximum strain acting on the fil‐ter screen for different materials of filter screen

4 结论

1）通过对气相流体和固相流体的密度及黏度、流体的流动速度、流通面直径等因素进行无量纲化，得到滤网应变与流体的流动速度呈二次函数关系，与固体杂质颗粒的质量流量呈一次函数关系，与气相流体的物理性质有关，随滤网材料弹性模量的增大而减小。

2）在所模拟的同一种气相流体流动中，保持固体杂质颗粒的质量流量、颗粒直径等因素不变，只改变流体的入口速度，得到滤网最大应变与流体流动速度呈二次函数关系，与无量纲π理论推导所得公式中滤网应变与流体流动速度的量级一致。

3）在相同的气相流体流动中，保持流体的速度、固体杂质颗粒的直径等因素不变，只改变固体杂质颗粒的质量流量，通过模拟，得到滤网最大应变与固体杂质颗粒的质量流量呈一次函数关系，此结论与无量纲π理论推导所得公式中滤网应变与固体杂质颗粒的质量流量的量级一致。

4）保持流体的速度、固体杂质颗粒的质量流量、颗粒直径等因素不变，对比空气（Air）、甲烷（CH4）和氮气（N2）3 种不同的常见气相流体，得到滤网的应变与气相流体的物理性质相关的结论，与无量纲π理论所得公式中体现的结论一致。

5）在同一种气相流体流动中，保持流体的速度、固体杂质颗粒的质量流量、颗粒直径等因素不变，只改变滤网材料，通过模拟，得到滤网的应变随滤网弹性模量的增大而减小，与无量纲π理论推导所得公式中滤网应变与滤网弹性模量的关系一致。