基于差分进化算法的运输直升机人员装载问题

田 野，田卫萍，李文龙，范文超

（北方自动控制技术研究所，太原 030006；2.驻太原地区第二军代室，太原 030006）

0 引言

直升机因其具有灵活的机动性、低空隐蔽性等特点，逐渐成为现代战争中不可缺少的作战力量，空中机降作战随之成为一种重要作战方式。因此，依据作战任务和作战人员乘载原则，快速地生成合理有效的运输直升机乘载人员分配方案，对于提高作战效率、减少直升机资源浪费、节省时间成本具有重要作用。

运输直升机人员装载问题实质是一个离散空间的多约束组合优化问题，同时也是典型的NP 问题［1］。当前，对此类问题的求解方法可分为以线性规划为代表的传统算法，和以遗传算法为代表的智能优化算法［2-5］两类。传统算法求解效果精确，但大规模的组合优化问题受限于计算量，求解速度较慢，效率较低。相较之下，智能优化算法通过不同的搜索策略和优化搜索机制，可以较快地处理大规模数据并得到较优的解。智能优化算法已逐渐成为求解复杂组合优化问题主要的有效方式。

为了实现对直升机资源高效的使用，减少资源浪费，本文在满足装载原则的前提下，建立了以直升机空间利用率最大化为目标的人员装载模型，并提出一种动态的差分进化算法对该模型进行求解。

1 运输直升机人员装载问题

1.1 问题描述

运输直升机人员装载问题的核心是在现有运输直升机资源有限的情况下，满足作战人员直升机装载原则的前提下，以尽可能高的空间利用率和尽可能少的直升机完成作战人员的分配装载。

其中，装载原则如下：作战人员直升机装载分配过程中，应尽量保持战斗编组和建制的完整性，保证乘机人员机降后保持一定战斗力；多位指挥员不搭乘同一架直升机，避免指挥员伤亡造成部队战斗力大幅下降。

同时，作战人员装载分配过程中受到可用直升机的机型、数量、不同机型直升机的容量（座次）和可承载重量等约束的限制，而直升机的容量和可承载人员重量又与实际作战半径（是否需挂载副油箱）等因素有关。如何处理约束条件和装载原则是求解直升机人员装载问题的重要部分。

1.2 数学模型

设有k 种不同机型的运输直升机，第i 种机型直升机最大可用数量为ni（i=1，2，…，k），该型直升机在作战距离为s 时，最大人员容量为，可承载人员重量为。

设有t 个待乘机建制班，为保证乘机人员战斗力，以作战小组为基本登机单位，将t 个建制班分为m 个具有独立作战能力的作战小组（指挥员单人成组），第h（h=1，2，…，m）个作战小组的人数为Nh，人员及携带装备重量为wh。

假设直升机作战距离一定，针对单波次运输直升机人员装载问题，基于最大的直升机空间利用率建立如下数学模型：

1）目标函数

该式表示所使用直升机的空间利用率。其中，numi表示最终装载方案所使用的第i 型直升机数量。

2）约束条件

直升机数量约束：

容量约束：

载重量约束：

装载原则约束：

其中，xijh= {0，1}，xijh=1 时，表示第h 个小组乘坐第i型机中的第j（j=1，2，…，ni）架直升机，ph为指挥员标志，取值范围为{0，1}，ph=1 时，表示第h 个小组为指挥员。

2 差分进化算法

2.1 算法描述

本文求解直升机人员装载问题采用的差分进化算法主要思想如下：随机生成初始种群，将种群中任意两个个体的向量差与第3 个个体求和产生变异个体；变异个体与父代个体交叉重组产生子代个体；对子代个体与父代个体间进行选择操作，将适应度更高的个体保留下来；不断进化迭代保留优良个体，逐渐逼近最优解。

本文提出的动态差分进化算法具体流程如下页算法1 所示。

2.2 编码设计

首先，对可用的k 种机型直升机依据型号数量按顺序编号。其次，采用整数编码方式对解方案进行描述：染色体上的每一位基因代表一个作战小组，该基因位的数值代表该作战小组搭乘的直升机编号，如图1 所示。这种编码方式与实际问题比较切合，直观易懂，同时满足直升机数量约束，见式（2）。

图1 编码方案

算法1 差分法进化算法Input：Population：pop；Dimension：n；Generation：T Output：The best solution：Δ 1.t←1（initialization）2.while（t≤T）or（f（Δ）is not same in l generation continuously）do 3. if f（Δ）is the same in h generatiaon continuously and f（Δ）≤fo then 4.F=F+rand（0，1）5. Cr=Cr-rand（0，Cr）6.end 7. （Mutation and Crossover）8.for i=1 to pop do 9.for j=1 to n do 10. vi，j t+1=Mutation（xi，j t ）11.ui，j t+1=Crossover（vi，j t+1，xi，j t ）12.end 13.（One to One Survival Selection）14.if f（ui t+1）＞f（xi t）then 15.Δ ←ui t+1 16.else 17.Δ ←xi t 18.end 19.end 20. t←t+1 21. end 22. return the best solution Δ；

2.3 约束处理

现有的启发式算法多用惩罚策略、竞赛选择机制、基因修复策略［2］等方法对约束进行处理。其中，惩罚策略和基因修复策略对可行域大小要求较高，当初始种群中可行解较少甚至毫无可行解时，这两种策略作用都不明显。

相较来说，竞赛选择机制对初始种群个体是否可行要求较低，更适合处理人员分配问题求解时随机生成的初始种群可行解较少的情况。因此，本文采用竞赛选择机制处理约束：

1）如式（6）所示创建违反约束程度矩阵CV。

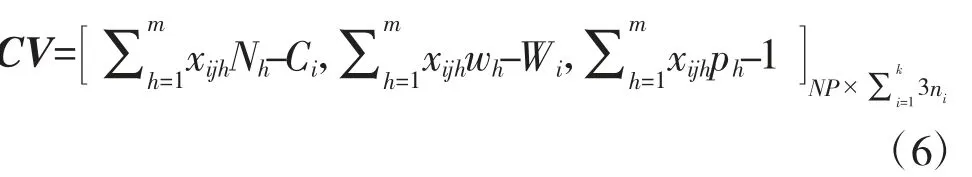
该矩阵中，列表示直升机装载状态，行表示该行所对应的种群个体违反约束程度，若CV 中存在元素cvij≥0，则表示该种群第i 个个体对应的解方案违反约束，为不可行解。若CV 第i 行元素皆小于0，表明该行对应个体为可行解，且CV 中的元素越接近于0，该方案对直升机利用率越高。

2）依据违反约束程度矩阵和种群目标函数矩阵（ObjV）来计算种群适应度（fitness），具体处理原则如下：满足约束个体的适应度高于违反约束个体的适应度；对于满足约束的个体，目标函数值越大，适应度越高；对于不满足约束的个体，违反约束程度越低，适应度越高。

这种约束处理方法保证了可行解对于非可行解的绝对优势，引导进化向可行方向进行，对不可行解的温和处理在一定程度上保持了种群的多样性。

2.4 参数处理

差分进化算法（DE）的控制参数包括种群规模（NP）、交叉概率（Cr，Cr∈［0，1］）和差分权重（F）［8］。NP 反映种群信息量大小；Cr反映父代个体与实验个体交叉重组过程中信息交换程度，通常取值范围为Cr∈［0，1］：F 决定差分向量的放大比例，反映算法的全局寻优能力，通常取值范围为F∈（0，2）。F和Cr两个参数决定着整个算法的搜索效率。

为保证较少的计算量和较低算法时间代价，本文提出的算法在较小的种群规模基础上调整参数Cr和F 来改进算法性能。同时，为保证实际工程中的求解质量，本文在算法中加入预设个体适应度f0，通过对待乘机人员和直升机数量性能的初步估算，给出预设个体适应度f0（即预设目标函数）。具体处理方式如下：在给定初始参数Crinit和Finit的情况下，当进化过程中连续h 代种群最优个体适应度停滞在某一值不变时，且种群最优个体适应度小于预设个体适应度f0时，认为算法陷入局部最优解，此时应调整参数提高种群多样性，即增大差分权重F 的值（F=F+rand（0，1）），提高全局寻优能力，促使算法跳出局部最优解；同时，为避免差分权重F 增大导致算法局部搜索能力变差的风险，减小交叉概率Cr的值进行平衡（Cr=Cr-rand（0，Cr）），保证一定的局部搜索能力。

这种控制参数随进化代数和种群最优适应度变化的动态参数处理方式，可以有效地改善传统差分进化算法进化过程中易产生的陷入局部最优、早熟等缺点，有效平衡了算法的全局搜索能力和局部搜索能力。

2.5 迭代过程

2.5.1 变异策略

本文采用的动态精英变异策略如下页图2 所示。变异的基础是差分向量，即个体通过与种群中个体间的差异作矢量和进行变异。种群初始进化时，个体间差异较大，变异范围更广泛，全局搜索能力更强。随着进化代数增加，种群趋向某个极值进化，个体间差异变小变异被局限在某个范围，种群多样性锐减，搜索将陷入停滞进入早熟状态。此时由图2 可以看出，上调参数F 可以扩展个体的变异范围，算法搜索范围变大，跳出局部极值。

图2 差分变异策略

这种变异策略选取精英个体作为基向量，在可行精英解附近域进行变异，有利于进化向最优解方向发展。而动态的差分权重参数使得种群多样性不随进化过程锐减，始终保持一定的种群多样性，保证算法不陷入早熟。

2.5.2 交叉策略

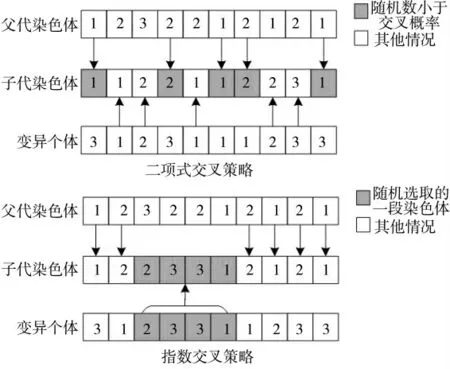
图3 交叉策略

差分进化算法常用的交叉方式分为两种（如图3）：二项式交叉和指数交叉［10］。其中，二项式交叉是针对父代染色体和变异个体的每一位进行交叉互换，指数交叉则对变异个体和父代个体上某一段基因进行交叉操作。2.4.1 节所述的变异策略很大程度上拓展了算法全局搜索能力，二项式交叉策略精确到基因的操作更容易保证局部搜索能力（当Cr取较小值时，交叉基因位数变少，可以充分对变异个体领域进行搜索）可以抵消变异策略，导致算法的局部搜索能力较差的后果。

根据2.3 节所述，在进化过程中，当参数F 增加时，减小交叉概率Cr=Cr-rand（0，Cr），提高局部搜索能力，对进化过程进行微调，平衡差分权重F 增加带来的算法局部搜索能力变弱错失更优解的弊端。

2.5.3 选择策略

本文采用一对一生存选择策略生成新一代种群：将交叉生成的子代染色体与其父代基向量染色体进行比较，排除适应度低的个体，选择适应度高的个体作为新一代种群个体。该策略保留父代精英个体，规避了因变异交叉操作丢失最优解的风险。

2.5.4 终止条件

本文同时使用两种终止条件结束进化过程：当迭代过程达到最大进化代数时，进化终止；连续l（l＞h）代种群最优个体适应度或目标函数值保持不变时，进化终止。两个终止条件相互制约，保证算法收敛同时尽可能缩减时间代价。

3 仿真测试

3.1 实例测试

为验证模型及算法可用性，本文采用如下用例进行测试：假设现有待乘机人员可分为22 个作战小组，参数如下页表1 所示，可用直升机参数如表2所示。设差分进化算法初始差分权重F=0.5，交叉概率Cr=0.5，预设个体适应度f0=90%，基于Python 语言编写代码对运输直升机人员装载问题进行求解。

运行差分进化算法求解得到的作战小组分配方案如表3 所示，共使用6 架直升机（3 架I 型，3 架II 型），总空间利用率为96.97%。实验结果表明，本文提出的差分进化算法可以较好地解决运输直升机人员装载问题，分配方案满足装载原则，直升机空间利用率很高。

表1 待乘机人员参数

表2 可用直升机参数

表3 运输直升机人员装载方案

3.2 算法分析

以3.1 节测试用例为例，采用遗传算法（GA）、传统差进化算法（DE）和本文提出的动态差分进化算法（动态DE）分别对该用例进行测试。

图4 各类算法迭代图

图4 所示为3 种算法对于该用例分别迭代500代的结果，可以看到相较DE 和GA，本文提出的动态差分进化算法具有更快的收敛速度和较好的求解质量，动态变异算子和交叉算子使得算法进行快速搜索，可以较快地得到高空间利用率的直升机人员装载方案。

表4 所示为3 种算法对测试用例进行120 次测试的结果。测试过程中，遗传算法多次出现无可行解的情况，而传统差进化算法求解质量较为一般。可以看出，针对运输直升机人员装载问题，本文提出的动态差分进化算法求解效果更稳定，可以大概率地获得优质的人员装载方案。

表4 各类算法结果比较

4 结论

本文针对运输直升机人员装载问题这一多约束组合优化问题，提出了一种动态的差分进化算法，该算法在传统差分进化算法的基础上，对控制参数差分权重和交叉概率进行了调整，使其随迭代效果进行变化，平衡了算法全局搜索能力和局部搜索能力，改善了传统差分进化算法进化后期种群多样性锐减、易早熟等缺点。第3 章实验测试对该算法的求解效果进行了验证，表明该算法可以在满足装载原则的条件下，更快地得到高空间利用率的直升机人员分配方案。