基于BP神经网络的桥梁移动荷载识别精度

赵 煜， 李冉冉， 周勇军， 田瑞欣

(1.长安大学公路学院， 西安 710064； 2.长安大学公路大型结构安全教育部工程研究中心， 西安 710064)

随着经济社会的不断发展，桥梁上行驶车辆的重量、数量在不断增加，导致中国现有诸多在役桥梁未达到设计寿命就提前结束服役，车辆的超载是重要原因之一。因此从桥梁管养角度出发，迫切需要对桥梁上的车辆负载进行监测，从而保证桥梁的正常使用[1-2]。

确定移动荷载的方法可分为直接法和间接法。直接法是直接测量出荷载大小或测量与荷载有关的参数进而换算出荷载的大小，然而移动荷载测试设备高昂的安装和维修保养费用大大增加了桥梁的建设成本。对于工程结构，比较容易获取的是结构的动态响应，因此一些学者提出基于结构实测响应反算荷载的间接识别方法，即荷载识别技术。荷载识别是通过测量结构的响应(应变、位移、速度、加速度等)，根据已知结构动态特性来识别作用在结构上的荷载。韩万水等[3]提出了基于有限元模型修正的单车通过多梁式桥梁的移动荷载识别方法。王宁波等[4-5]根据桥梁动应变曲线峰值点识别车辆行驶速度、轴数、轴距，并用影响线拟合动应变响应来识别车辆各轴轴重。钱长照等[6]利用影响线建立移动荷载与弯矩之间的关系，提出了一种利用弯矩影响线进行移动荷载识别的方法。邹谭[7]基于剪切应变影响线提出了识别单一车辆荷载的新方法,根据剪切应变影响线的特征不仅能识别车辆轴重和总重,还能识别车速和轴距。左小晗[8]对多车过桥荷载识别问题进行了研究，将多车问题转化成单车问题加以解决。Fitzgerald等[9]基于正则化技巧，准确地计算出了车辆轴载。Chen等[10]开发了一种预处理最小二乘分解法，可以减少未知噪声引起的识别误差，并在简支梁上验证了该算法的有效性和适用性。

近年来，一些学者将人工神经网络方法用于移动荷载的识别。误差反向传播(back propagation, BP)神经网络是一种常用的神经网络，具有多输入和多输出的计算特点，BP 神经网络可在一定程度上解决不适应导致的求解困难问题。根据桥梁的挠度、应变等响应识别桥梁动载已有很多学者对此进行研究，并取得了一些成果。李忠献等[11]基于BP神经网络，提出了一种分阶段识别桥上移动荷载的新方法，分步识别了车辆的位置、速度和荷载；结果表明：所提出的方法能够实时地识别桥上移动车辆荷载，且具有识别精度高、收敛速度快的优点。杨慧等[12]利用BP神经网络以及桥梁动应变响应对车辆的位置、速度和大小进行了识别，通过模型试验验证了BP神经网络用于桥上车辆荷载识别的可行性。陶兴旺等[13]采用斜拉桥实际运营状态下的监测响应 ( 索力和应变)组成网络的输入向量，对通过斜拉桥的重车荷载识别进行了探讨。陈修辉等[14]提出了一种基于分层菌王觅食算法(HKBFO)的桥梁动载识别方法，该方法提高了BP神经网络对桥梁动载识别的效果。

由上述可知，将神经网络用于移动荷载识别时需要确定有效的网络输入参数、输出参数、网络结构以及算法等，这些参数对识别的准确性和稳定性均有重要影响。目前大多数学者集中于网络结构及算法的研究，对输入参数的相关研究较少，且存在一些输入参数不便获取和单参数输入无法得到理想结果的问题。现采用BP神经网络方法进行桥梁移动荷载大小的识别，以识别精度为量化指标分析了位移、速度、加速度单输入参数的敏感性。同时针对单参数输入识别过程中不稳定和识别精度不高的问题，基于BP神经网络多输入多输出的特点，提出了多参数优化设计来提高网络的收敛速度和精度。最后通过实桥试验验证了该BP神经网络识别移动荷载的实用性和准确性。相关研究成果一方面可以为智能交通运输提供参考，另一方面可为桥梁全寿命周期的管养提供数据支持。

1 移动荷载识别理论

以简化的Bernoulli-Euler梁为例，其跨度为L，桥梁单位长度质量为m，抗弯刚度为EI，桥梁阻尼取黏性阻尼c，忽略桥梁的剪切变形和转动惯量。车辆模型简化为一移动集中力，大小为P(t)，车辆移动速度v视为匀速，从桥梁一端向另一端行驶(此处假定为从左向右单向行驶)，如图1所示。

系统运动方程可写为

δ(x-vt)P(t)

(1)

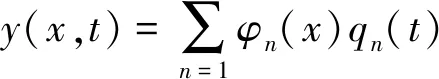
(2)

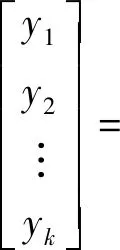
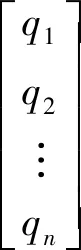
(3)

记为

y=sq

(4)

通过速度识别可得y，运用最小平方法求解式(4)可解得桥梁的位移模态，即

q=(sTs)-1sTy

(5)

同理可解出模态下的加速度和速度。

将式(2)代入式(1)，方程两边同时除以m可得

n=1,2,3,…

(6)

式(6)等号双边同时倍增φj，并将x从0～L进行积分，可得

n=1,2,3,…;j=1,2，3,…

(7)

由振型正交性原理应用式(7)模态响应等式

n=1,2,3,…

(8)

式(8)中：

为第m个荷载和第一个荷载相隔的距离。

式(8)可化简为

(9)

移动荷载P可以通过最小平方法原理求得

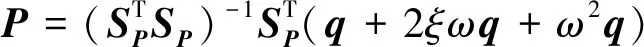
(10)

2 基于BP神经网络的移动荷载识别

2.1 BP神经网络模型

基本的BP神经网络如图2所示，由输入层、隐含层和输出层等基本结构组成，是一种非线性映射关系。图2中有n个输入节点，m个输出节点，网络的隐含层有若干个神经元结构。其中，x1，x2，…，xn为网络的实际输入，y1，y2，…，ym为网络的实际输出，tk(k=1，2，…，L)为网络的目标输出，ek(k=1，2，…，L)为网络的输出误差。BP神经网络的每一层权值都可以通过学习调节。

图2 BP神经网络模型Fig.2 BP neural network model

BP算法的基本原理较为简单，采用的是梯度最快下降法，即通过大量的样本训练，不断地调整网络中隐含层的连接权值，通过不断的使实际输出逼近期望输出，来使整体网络系统的总误差最小。

2.2 基于BP神经网络进行荷载识别的方法

利用BP神经网络进行荷载识别时，首先需要根据桥梁在不同状态(不同的车辆速度，不同车辆位置和不同轴重)的反应，通过特征提取，选择对荷载识别参数较敏感的信号作为输入向量，桥上移动车载的识别参数作为输出，获取数据样本并去除噪声从而获得尽量逼真的原始数据。在原始样本的基础上，进行适当变换，得到适合神经网络识别的样本的表达式。以上两步构成神经网络识别中的预处理过程。然后选择适当的网络结构并采用适当的学习算法，用已知样本作为训练集对网络进行训练，使其网络连接的权值不断调整，直到网络的输出特性与期望的相符合。识别步骤如图3所示。

实际工程中，桥梁响应通过健康监测系统数据采集系统得到，实测数据包含着各种因素，如环境噪声、结构自身振动噪声等，需要人为的进行处理，去除噪声，以避免一些微小的因素影响网络的识别精度。而本文仅作数值理论分析，桥梁响应是通过计算机仿真计算获得的并且都是理想状态下的数据，所以不需要进行常规处理。

3 仿真分析模型

利用神经网络法进行荷载识别最重要的是确定输入参数和输出参数，如果输出信号对输入不敏感，网络的逼近能力就很差，很有可能达不到要求。以一个跨径为30 m的装配式简支梁上作用移动荷载为研究背景，通过数值仿真分析获取移动荷载通过桥梁时的动态响应，理论上分析不同的输入参数对移动荷载大小识别精度的影响。

桥梁总宽15 m，单片梁宽2.5 m、高2 m，共6片T形梁，材料为C50混凝土。T形梁横截面如图4所示。利用ANSYS参数化语言建立简支T形梁的梁格模型，主梁和虚拟横梁均采用beam188单元模拟，采用自由网格划分，确保网格大小符合计算精度。鉴于工程中更加关注车辆总体的重量，这里将车辆简化为一移动集中力，利用ANSYA动力瞬态分析方法求解动力响应。ANSYS有限元模型如图5所示。

图5 ANSYS有限元模型Fig.5 ANSYS finite element model

4 单输入参数敏感性分析

假定上述简支梁桥上作用单个时变移动荷载P=200 kN×(1+0.25sin2πt)(随时间规律变化的荷载)，由于汽车受到路面不平的激励后以车的固有频率发生振动而通过桥梁时, 汽车的惯性力是一种简谐力, 所以讨论这种移动的简谐力所引起的强迫振动是很有意义的。同时为了使得网络的函数映射关系更加简单从而实现较高的识别精度，这里将移动的行驶速度和位置固定来剔除这两个因素的影响，即假定移动荷载以v=20 km/h速度匀速行驶于1#梁上。通过 ANSYS仿真分析分别得到移动荷载作用下1#梁跨中位移、速度和加速度时程曲线如图6所示，数据采集时间为5.9 s，时间步长Δt=0.02 s，每组样本采集322个样本数据点，以此数据作为输入参数，移动荷载的大小作为输出参数，通过MATLAB构建BP神经网络模型，对网络结构进行训练。

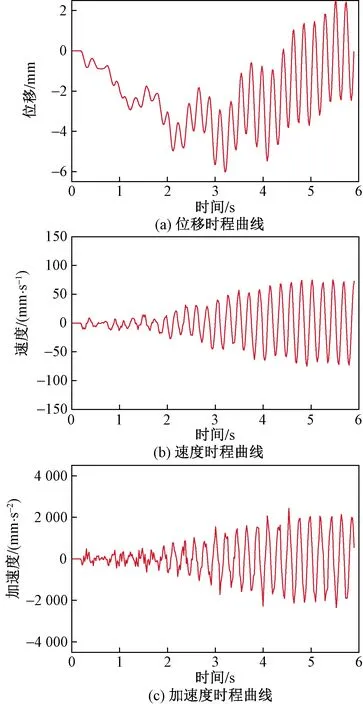
图6 时程曲线Fig.6 Time history curve

将时变荷载作用下1#梁跨中位移、速度和加速度响应数据代入学习训练成功的BP网络中，利用BP神经网络的高度非线性逼近能力实现荷载的大小识别，最终将移动荷载的大小作为输出参数输出。图7为跨中截面时变荷载识别结果。

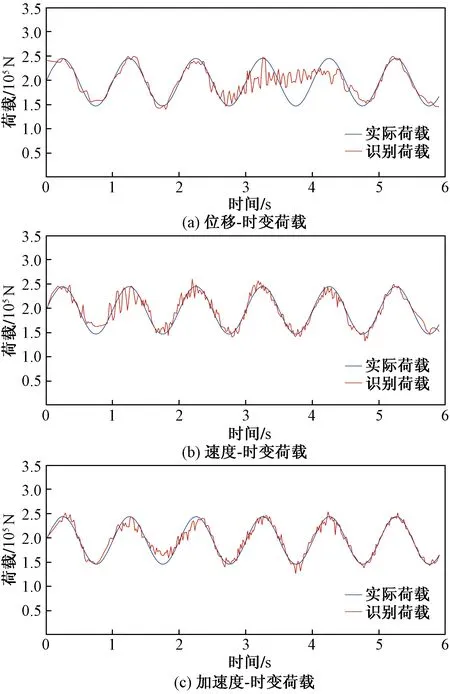
图7 单参数输入荷载识别结果Fig.7 Load identification results of different input parameters

由图7可以看出，位移输入时3～4 s内识别荷载与真实荷载偏差较大，识别过程出现局部振荡现象。速度输入识别效果要优于位移输入识别效果，整体上识别荷载贴近真实荷载，但局部仍然存在微小偏差状况。加速度输入识别效果优于位移输入和速度输入识别效果，识别荷载更加贴近真实荷载，但局部仍然存在识别荷载曲线不光滑状况。

为了评价BP神经网络识别的精度，衡量识别参数与真实参数之间的差距，现引入为相关系数R的概念，R越接近于1表示相关程度越高，其计算公式为

(11)

将1#梁跨中位移、速度和加速度3种移动荷载动态参数作为BP神经网络的输入参数进行敏感性分析，分析结果如表1所示。

表1 单输入参数敏感性分析结果

通过表1可以看出，选择相同的采样时间和采样数量进行BP神经网络识别，其中加速度的训练步数最长，约为位移和速度的两倍，位移和速度的训练步数接近。加速度的相关系数最大，为 0.946 62，表明加速度的识别精度要优于速度和位移的识别精度，这与识别结果图相吻合。

在实际工程中，桥梁的加速度时程曲线更容易获取，故建议在实际工程中采用加速度输入参数进行荷载识别。由识别结果图可以看出，尽管加速度识别已经达到较好的识别效果，但仍然存在局部拟合偏差、识别曲线不光滑等问题，故论文基于输入参数敏感性分析，提出多输入参数优化设计来完善识别过程、提高识别精度。

5 多输入参数敏感性分析

BP神经网络多参数输入的优点是当网络数据存在部分异常以及缺失时，可以依靠多输入的对应关系给予优化弥补。这里分为位移和速度输入优化、位移和加速度输入优化、速度和加速度输入优化两两组合的工况以及位移、速度和加速度三者组合的工况进行输入参数的优化设计。

选取1#梁跨中时程曲线数据作为输入参数构建训练样本，采样时间和采样数量均与单参数保持一致，即数据采集时间为5.9 s，时间间隔设为0.02 s，每组样本采集322个数据点。基于 MATLAB 构建BP神经网络模型，利用BP神经网络的高度非线性逼近能力实现时变荷载的大小识别，并通过相关误差判断识别精度，图8所示为跨中截面时变荷载识别结果。

将图8与图7进行对比可以看出，多参数组合输入一定程度上可以提高识别精度，优化识别过程，使识别荷载进一步逼近真实载荷，同时可以提高识别过程中的稳定性。具体来看，位移和速度输入得到的识别荷载与实际荷载曲线整体上较为接近，仅局部存在微小偏差，识别效果远优于位移单参数输入。位移和加速度输入识别弥补了位移输入识别局部偏差较大的不足，同时改善了加速度识别曲线不光滑的现象。速度和加速度输入识别曲线非常接近真实载荷的曲线，且曲线光滑无局部偏差峰值，可以明显地减小局部振荡现象的产生。将位移、速度和加速度三参数组合输入得到的识别曲线出现锯齿状，虽然整体较为贴近真实载荷，但曲线光滑度降低，表明识别效果有所下降。多参数输入识别结果总结如表2所示。

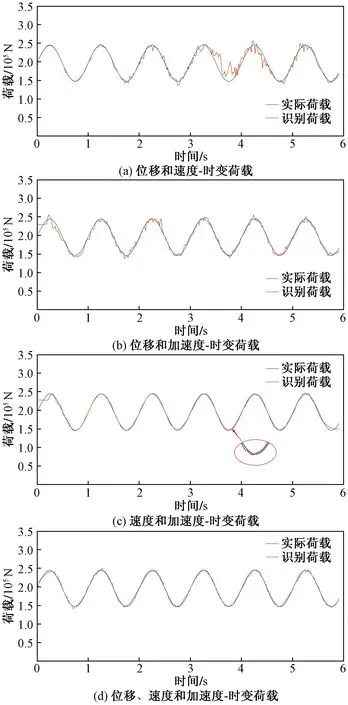
图8 多参数输入时变荷载识别结果Fig.8 Time varying load identification results with multi-parameter input

通过表2可以看出，采样数量和训练步数与相关系数并无线性关系，而是与输入参数紧密相关。速度和加速度组合输入得到的识别荷载与真实荷载的相关系数为0.970 95，是4种参数组合中识别过程最稳定、识别精度最高的组合，可以实现优异的识别效果。

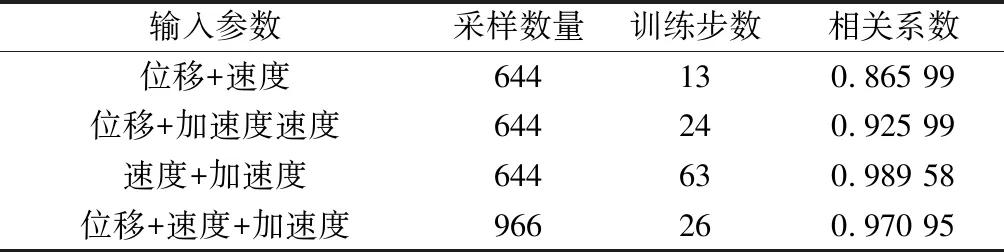
表2 多参数输入敏感性分析结果

6 工程实例分析

6.1 工程简介

椒江北枢纽主线桥全长2 727 m，全桥共29联，试验选取第1联(4×30 m)第2、4跨进行荷载试验。桥宽16.25 m，净宽15.25 m，横桥向共布置7片梁。试验截面为第4跨跨中处Ⅰ-Ⅰ截面、第2跨距2#墩2 m处Ⅱ-Ⅱ截面、第2跨跨中处Ⅲ-Ⅲ截面，如图9所示。在试验截面左右两侧分别布设加速传感器，传感器型号为941-B型拾振器，其测点布置如图10所示。

图9 桥梁测试截面布置示意图Fig.9 Layout of bridge test section

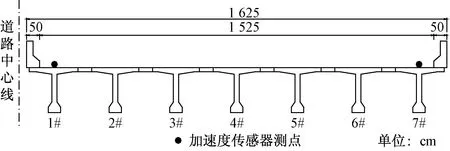
图10 加速度传感器测点横桥向布置示意图Fig.10 Layout of acceleration measuring points

6.2 移动荷载识别

首先建立有限元模型并对模型进行修正[15]，通过大量数值仿真分析数据组建和训练BP神经网络结构。设置8种模拟工况，采用383 kN和376 kN的加载车分别以20、30、40、50 km/h，4种不同的速度等级通过桥梁，总计8组，共计12 864个数据样本点，将多种工况下的桥梁动态加速度时程数据作为神经网络的输入样本进行训练。

然后，依托上述预应力混凝土连续T形梁桥荷载试验对BP神经网络进行验证性分析。实桥动载试验过程中，使一辆373 kN(试验前通过称重获知其前轴重62 kN，两后轴合计重311 kN，车型如图11所示)加载车以匀速30 km/h的速度沿着桥梁外侧车道行驶，获得I-I截面7#梁处的竖向加速度时程数据。为了滤除噪声对测试结果的影响，这里利用计算机对所得信号波形进行处理，处理后的加速度时程曲线如图12所示。

图11 试验用标准车车型Fig.11 Standard vehicle type for test

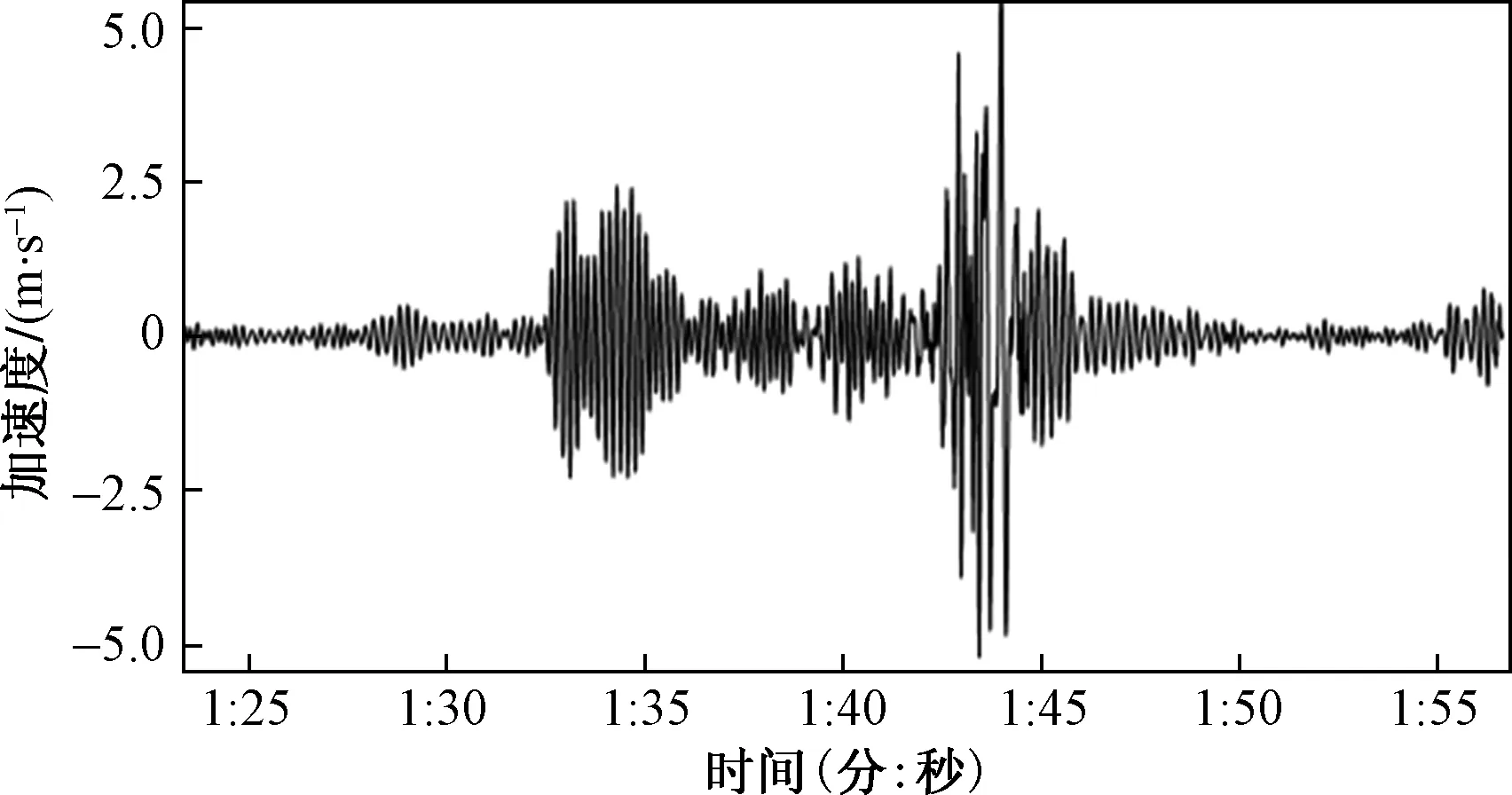
图12 Ⅰ-Ⅰ截面加速度时程曲线Fig.12 Acceleration time history curve

将实测加速度数据作为BP神经网络的输入参数，车辆的前、后轴重作为输出参数进行轴重识别验证分析。这样一方面可以保证BP神经网络的识别精度，另一方面可以得到更为准确的车辆轴载信息。试验获取7#梁共2 000个加速度时程数据点，前、后轴重识别结果如图13所示。经计算得，前、后轴重识别相关系数分别为0.925 6和0.944 7。

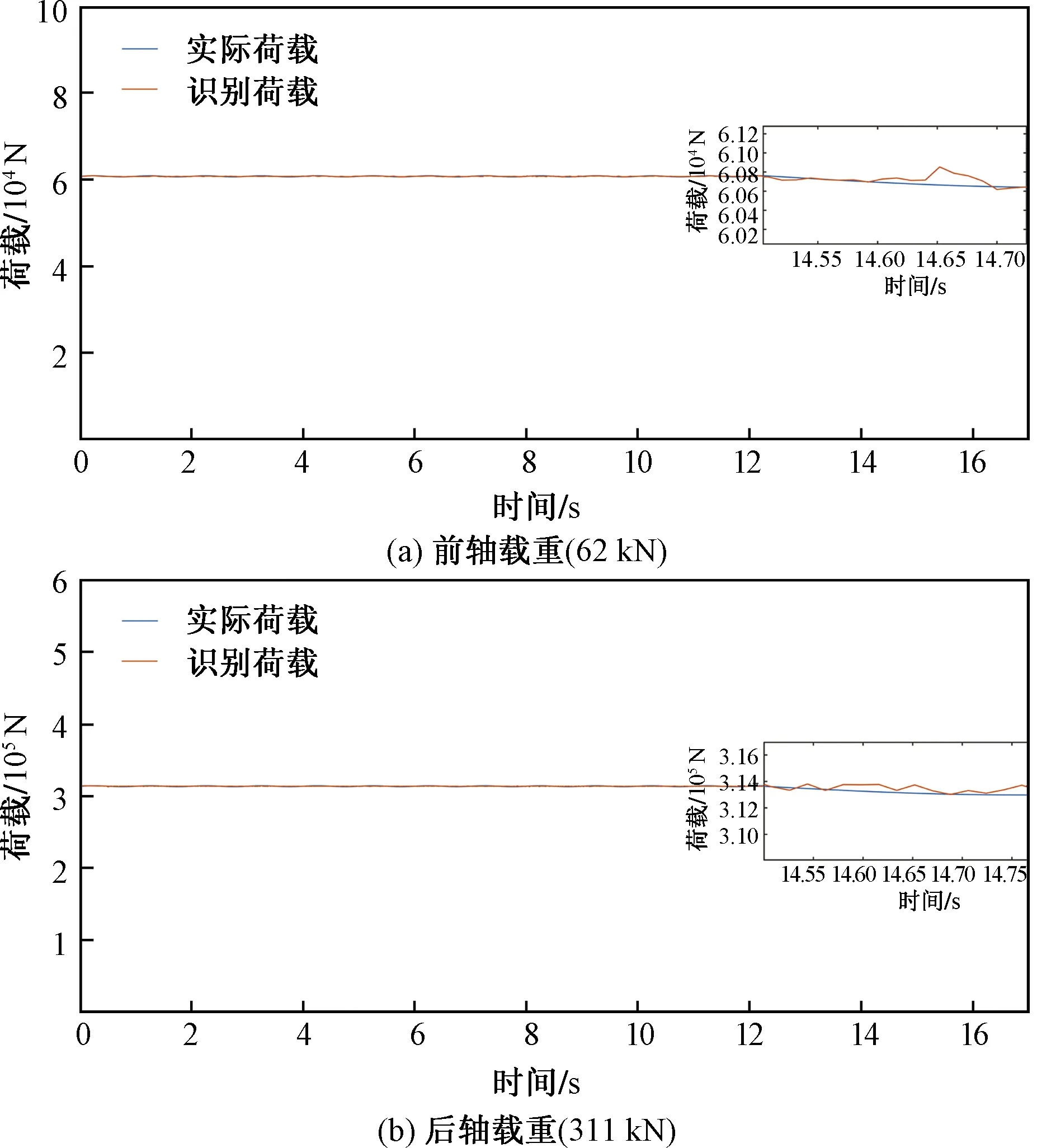
图13 前、后轴载重识别结果Fig.13 Identification results of front and rear axle weight

由上可知，采用实测的竖向加速度时程数据作为BP神经网络的输入参数，其前、后轴重的识别整体上具有较为满意的效果，识别荷载曲线与真实荷载曲线接近，表明了基于实桥的加速度时程数据也具有良好的载重识别效果，验证了该BP神经网络结构用于简单的实桥载荷识别的可行性。

7 结论

(1)针对同一BP神经网络结构，不同的输入参数得到的识别结果是不同的，采用加速度作为神经网络的输入参数可以提高识别精度，提升识别过程的稳定性；采用位移作为输入参数可能会出现局部振荡、与实际荷载偏差较大的现象。

(2)提出了多参数输入优化设计，通过位移、速度、加速度两两组合以及三者组合的输入方式进行识别对比发现，速度和加速度两者组合作为输入参数具有较为理想的识别效果，是多种参数组合中识别精度最高的一组参数组合；多参数输入优化设计可以改善神经网络的识别过程，提高整体和局部的识别效果。

(3)以某4跨预应力混凝土连续T梁桥工程为背景，完成了实桥载重识别的验证分析，结果表明该BP神经网络结构可用于简单的实桥载荷识别。

(4)研究了针对单一荷载的识别方法和识别精度问题，可为后续多个移动荷载的识别奠定理论基础，未来可进一步研究多车辆多种行驶状况下的移动荷载识别问题。