基于非解析计算流体力学和离散单元法的大颗粒在流场中的高效率运动模拟
熊书春, 臧孟炎
(华南理工大学机械与汽车工程学院, 广州 510640)
计算流体力学(computational fluid dynamics, CFD)与离散单元法(discrete element method, DEM)耦合模拟流-固两相流问题,已广泛应用于各种工程研究。其所需要的经验参数少,可方便地考虑颗粒尺寸分布,获得颗粒尺度的微观信息[1-2]。目前, 按照颗粒大小与流体网格尺寸的相对关系,可分为解析CFD-DEM方法和非解析CFD-DEM方法[3]。在解析CFD-DEM方法中,颗粒明显大于流体单元,一个颗粒会覆盖多个网格。常用的有浸没边界法(immersed boundary method, IBM)[4]等,可以精确地解析每个粒子周围的流场,并通过直接数值积分计算流体作用在每个粒子上的力[5]。而在非解析CFD-DEM方法中,考虑的颗粒明显小于流体单元,因此,一个网格可以包含多个颗粒。这类方法不精细求解每个颗粒周围的流场,而是基于曳力模型[6]在局部平均化的流场网格中将流体-颗粒相互作用模型化。
尽管IBM等解析CFD-DEM方法可用于高精度地模拟大颗粒在流场中的运动,但由于计算效率较低,研究大多局限于小数量的球形颗粒和二维情况下的规则非球形颗粒[7-8]。对于三维非球形颗粒,目前的研究也大多使用非解析CFD-DEM方法基于多球模型(multi-sphere model)近似模拟小于流体网格尺寸的较小颗粒的运动[9-11]。而多球模型的颗粒受力点为整体的质心,且有颗粒重叠时会在计算曳力时造成困难。不同于将所有组合球都作为一整个刚体运动的多球模型,黏结颗粒模型(bonded-particle model, BPM)可用无重叠的球形颗粒模拟各种形状[12-13]。为实现高效的大颗粒耦合数值仿真,在开源框架CFDEM中,实现了一种近似模拟大颗粒与流体耦合作用的新方法,将非解析CFD-DEM方法与BPM结合,模拟大颗粒在流体中的运动。
1 数值方法
1.1 控制方程
非解析CFD-DEM方法的控制方程是流相的连续方法和固相的离散方法的组合。不可压缩流体的运动由欧拉框架下的连续方法描述,基于CFD,求解连续性方程和局部平均的N-S(Navier-Stokes)方程得到每个网格尺度上的流场参数近似解,即

(1)
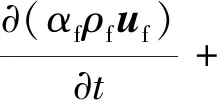
(2)
式中:αf表示由“分割法”[14]计算得到的网格中流体所占体积分数(孔隙率);uf为流体速度;τ=ν∇uf为黏性应力张量;ρf和ν分别为流体密度和运动黏度;Rs,f为基于曳力在每个单元中计算出来的流相与颗粒相的动量交换项。
固体颗粒由拉格朗日方法追踪,基于DEM对单个颗粒的运动分析通过求解牛顿运动方程得到,颗粒间的作用采用合理的接触模型描述。单个颗粒在基于DEM的拉格朗日框架中平移和旋转运动的控制方程表示为
(3)
(4)
式中:mi、Ii、ui、wi分别为颗粒的质量、转动惯量、速度和角速度;Fi,c表示颗粒间及颗粒与壁面之间的接触力;Fi,f为周围的流体作用在颗粒上的力,包括曳力、浮力等;其他外力(如重力、静电力或磁力)总结为Fi,b、Ti,c为颗粒i所受转矩。
1.2 黏结颗粒模型
颗粒可以基于BPM粘结在一起,形成大颗粒或不规则形状的颗粒,如图1所示。
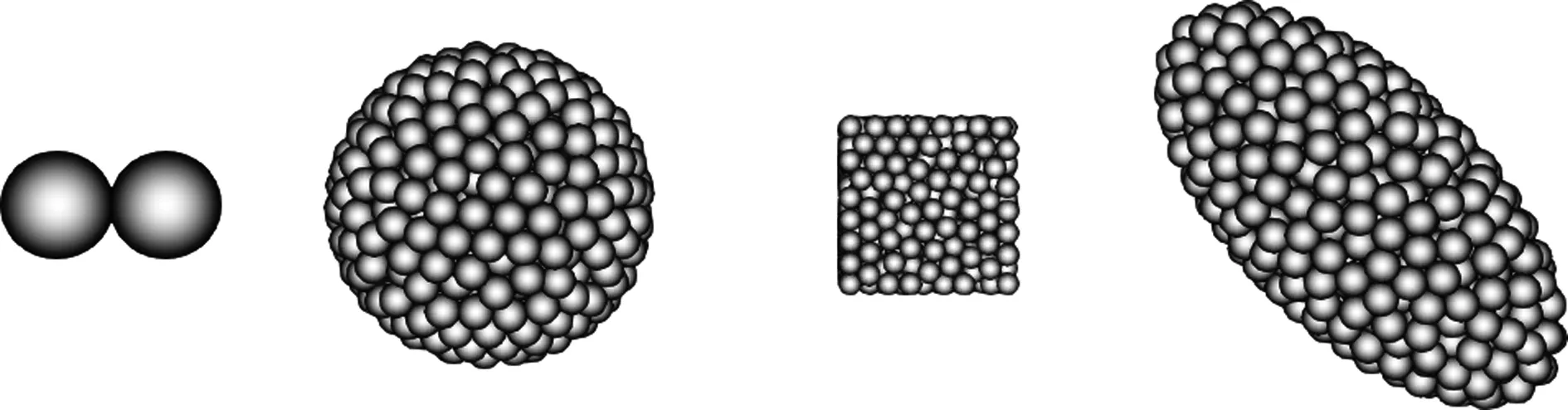
图1 黏结形成的颗粒Fig.1 The bonded-particles
该模型假定两个粒子通过弹簧-阻尼系统粘结在一起,表达式为
(5)
(6)
(7)
(8)
(9)
(10)
(11)
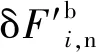
此模型采用虚拟的“黏结键”来黏结颗粒,这个黏结键可以承受切向和法向的微小位移,直到达到最大的法向和切向剪切应力。当法向和切向剪切应力超过设定的黏结强度时,黏结破裂,表达式为
(12)
式(2)中:r为黏结半径。
1.3 曳力模型
通过合理的耦合模型可以实现连续流体与离散颗粒之间的动量交换。Gidaspow曳力模型[6]用于模拟作用在每个小球颗粒上的流固相互作用力,表达式为
(13)
(14)
式中:ds和Vs为颗粒的直径和体积;μ为流体动力黏度。CD计算公式为
(15)
式(15)中:Res为颗粒雷诺数,定义为
(16)
式(2)中的动量交换项Rs,f计算公式为
(17)
式(17)中:n为网格中的颗粒数量;ΔVcell为网格体积;Fi,D表示网格中各个颗粒所受曳力。
1.4 非解析CFD-DEM方法结合BPM
提出一种近似模拟大颗粒与流体耦合运动的新方法,将非解析CFD-DEM方法与BPM结合,把一个大固体化整为零,可以近似地模拟占据多个网格的大颗粒在流体中的运动。
如图2所示,大颗粒直径为15 mm,小颗粒直径为1.5 mm,网格边长为5 mm。当颗粒大于流体网格尺寸时,可以用多个直径小于网格尺寸的小球形颗粒黏结形成大颗粒。因此,BPM可以满足非解析CFD-DEM方法的要求。在此方法中,无重叠量的小球粘结而成的大颗粒内部存在间隙,密度相同的情况下颗粒的总体积和总质量相较于原始大颗粒会变小。根据颗粒运动方程,为保证颗粒动力学计算准确,黏结颗粒各小球所受流体作用力的总和须对应同比例减小。
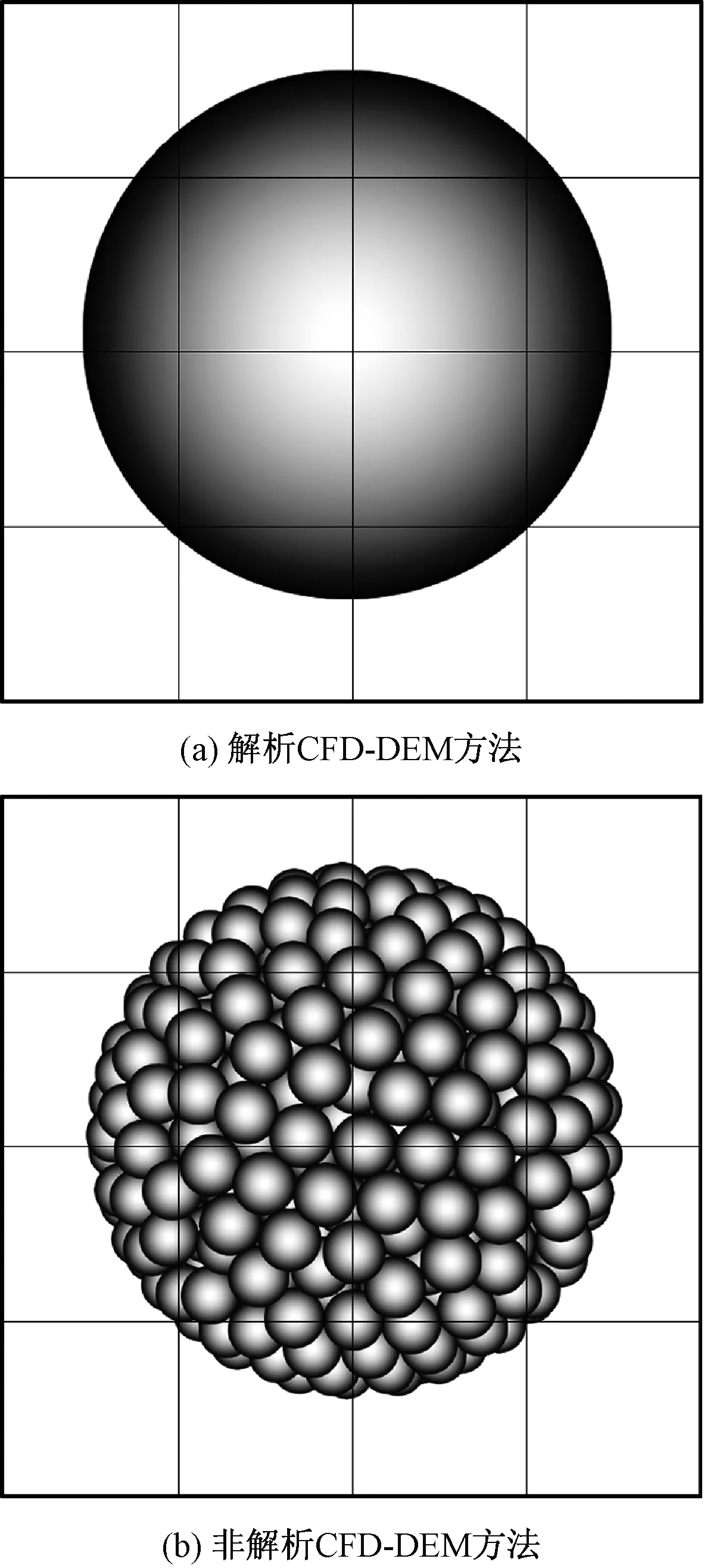
图2 流体网格中的大颗粒Fig.2 A large particle represented in fluid meshes
基于每个小球颗粒计算流体的作用力并将其分别施加在每个组成球上,不需要计算整体质心和转动惯量,这与将力施加到组合颗粒的质心的多球模型方法相反。由于每个黏结组成球所处流场的位置不同,流体作用在每个小粒子上的力可能不同,但是由于黏结键的作用,所有粒子宏观上都可以保持几乎一致的运动状态。总体而言,黏结力和力矩是内力,所有粒子运动参数的平均值可用于描述整个黏结颗粒的运动状态。在非解析CFD-DEM方法中,流体对球形颗粒无力矩作用,只对黏结的小球颗粒施加力在其质心上。但是,各个小球所受流体作用力相对于整个黏结颗粒的质心会产生力矩作用,且能通过黏结键传递,因此该方法可近似地表示流体对非球形大颗粒的力矩作用,模拟在流体中旋转的非球形颗粒。
由于非解析CFD-DEM方法和解析CFD-DEM方法计算流体对颗粒作用力的原理不同,且黏结颗粒内部存在间隙,因此必须修正曳力模型,使黏结颗粒所受流体曳力总和与大颗粒所受曳力之比等于质量之比,以保证黏结颗粒整体运动的准确性。引入校正因子K,即
(18)
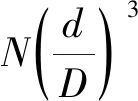
(19)
式(19)中:A为大颗粒的迎风面积。
尽管使用更多的组成球可以更准确地表示大颗粒的形状,但是计算效率会大幅降低。文中将小球的直径都设置为大颗粒(等效)直径的1/10左右,这可以同时满足计算方法对网格尺寸、计算准确性和效率的要求。根据颗粒的杨氏模量和泊松比来设置黏结键的法向和切向刚度,以保证键的精确变形。法向和切向黏结强度设置为足够大,可以防止黏结断裂。
该方法在开源框架CFDEM中实现,通过开源软件OpenFOAM的CFD求解器计算流场,LIGGGHTS软件基于DEM计算、更新颗粒的位置、速度、受力等信息,二者通过耦合接口进行质量、动量的传递和数据交换,实现并行双向CFD-DEM耦合。为保证耦合的稳定性和准确性,DEM时间步长应始终小于CFD时间步长。本文中CFD时间步长都设置为DEM时间步长的10倍,这意味着CFD和DEM的数据交换在耦合接口中每10个DEM时间步长进行一次。
2 研究方法验证
2.1 单个球形大颗粒沉降
分别使用结合BPM的非解析CFD-DEM方法和IBM方法模拟重力作用下单个球形大颗粒在黏性流体中的沉降运动,并与Cate等[15]的实验结果进行比较,验证数值方法的准确性。
如表1所示,设计了四组与Cate试验对应的算例,雷诺数由试验得到的颗粒稳态速度算出。大颗粒的直径为15 mm,密度为1 120 kg/m3,球体起始位置距底部高120 mm,重力加速度为9.81 m/s2。计算域为100 mm×100 mm×160 mm,两种方法的网格数都为25×25×40(IBM方法使用局部网格细化[3]),CFD和DEM的计算时间步长分别为1×10-5s和1×10-6s,BPM的黏结参数如表2所示。
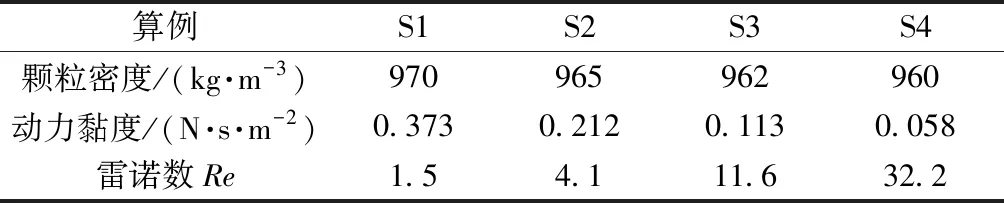
表1 实验和仿真参数Table 1 Experimental and simulation parameters

表2 黏结颗粒参数Table 2 Bonded-particle parameters
图3显示了在不同Re的条件下颗粒沉降速度、颗粒距底部高度与颗粒直径比值的时间历程。其中虚线表示非解析CFD-DEM方法结合BPM获得的数值计算结果(颗粒沉降速度与颗粒高度值都是615个颗粒的平均值),实线表示IBM的模拟结果,而散点符号表示实验结果。对比可知本文提出的仿真方法所得分析结果与IBM和实验结果一致性都很好,验证了该方法的有效性。
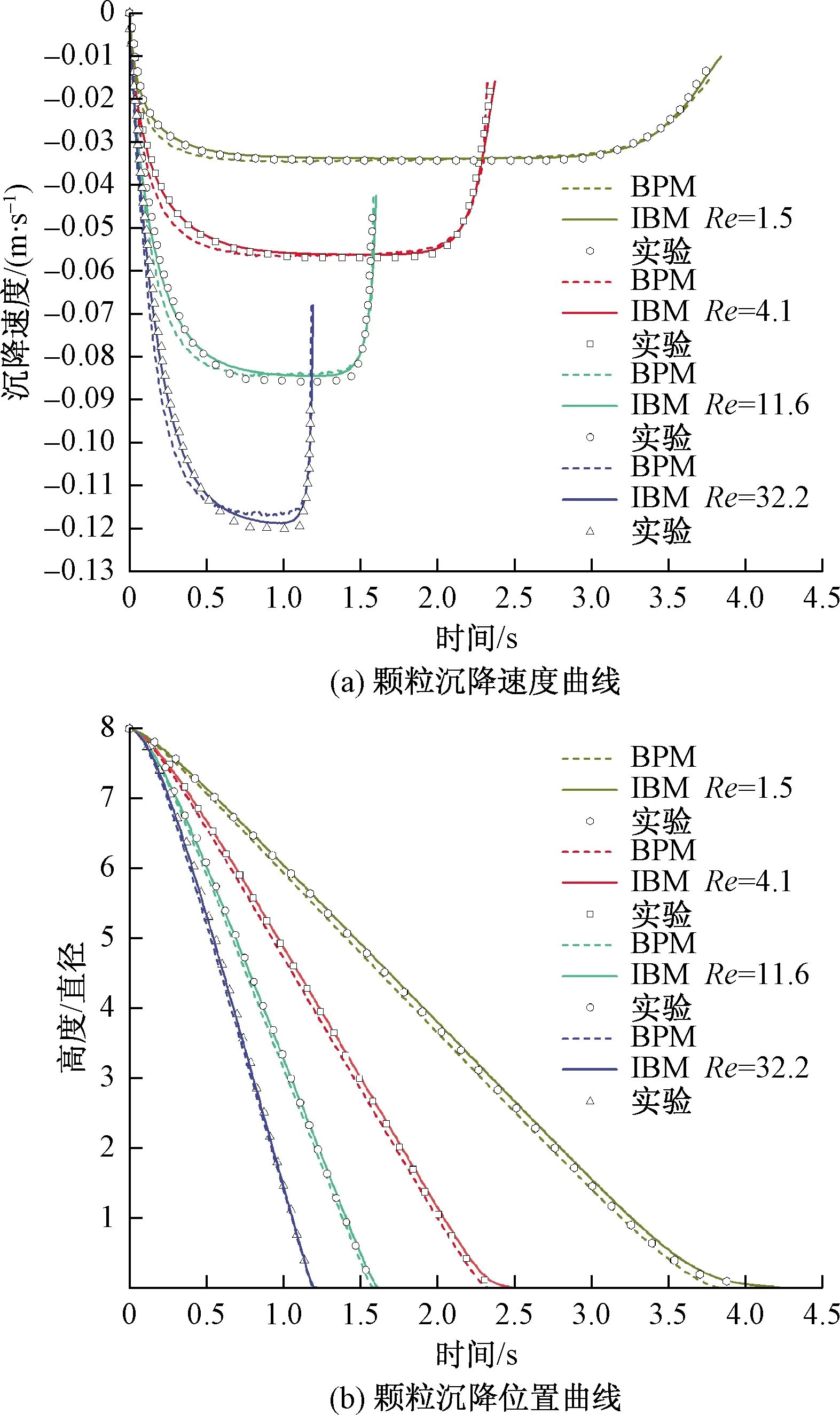
图3 仿真结果与实验对比Fig.3 Comparison of simulation results and experiments
2.2 计算效率验证
为了验证新方法的效率及其与大颗粒数量之间的关系,分别使用该方法和IBM模拟了重力作用下一个、四个和九个大球形颗粒在黏性流体中沉降的运动。流体密度为1 000 kg/m3,动力黏度为0.1 N·s/m2;大颗粒的直径为15 mm,密度为2 000 kg/m3,现象时间为0.5 s。
两种方法模拟所用CPU时间对比如图4所示,显然非解析CFD-DEM方法结合BPM的计算效率显著高于IBM。因为IBM需要颗粒周围非常精细的网格,且需要通过高精度的直接数值积分来计算曳力,尽管使用局部网格细化[3]减少了整体网格数量,但耦合计算过程仍耗时非常多。而本文提出的新方法,尽管BPM用多个小颗粒近似表达大颗粒,增加了离散元部分的计算量,但非解析CFD-DEM方法使用较粗的网格和标准化曳力模型确保了耦合计算效率。从图4中还可以看到,大颗粒数量越多,该方法的高效性越明显。
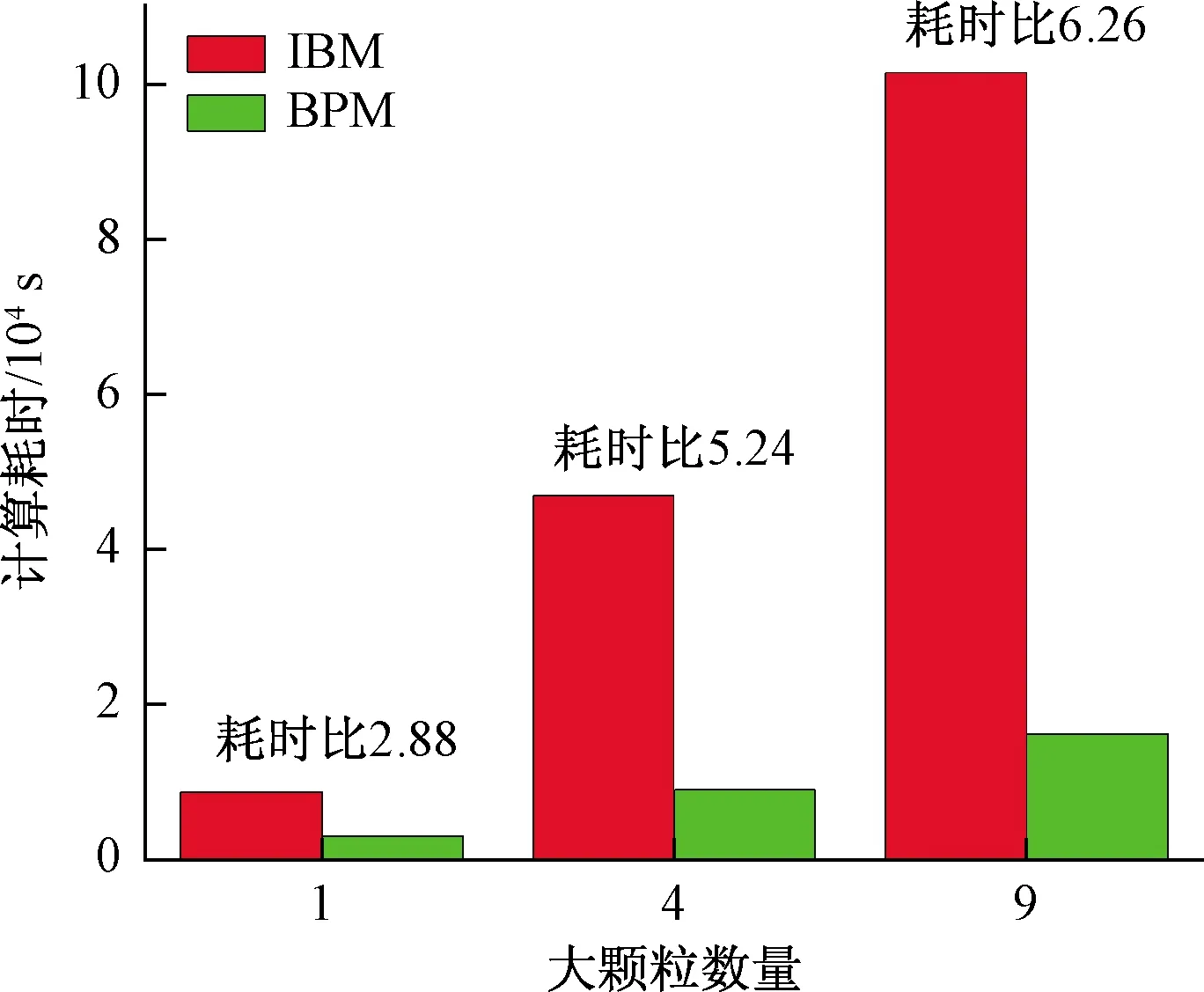
图4 两种方法计算耗时对比Fig.4 Comparison of calculation time between the two methods
3 非球形大颗粒的运动模拟
3.1 立方体大颗粒沉降
使用BPM表示立方体大颗粒,基于非解析CFD-DEM方法模拟其在黏性流体中的沉降,并且通过最大沉降速度仿真结果与表3所示的三组实验结果[16]进行比较,验证该方法对于模拟非球形大颗粒流场运动的有效性。
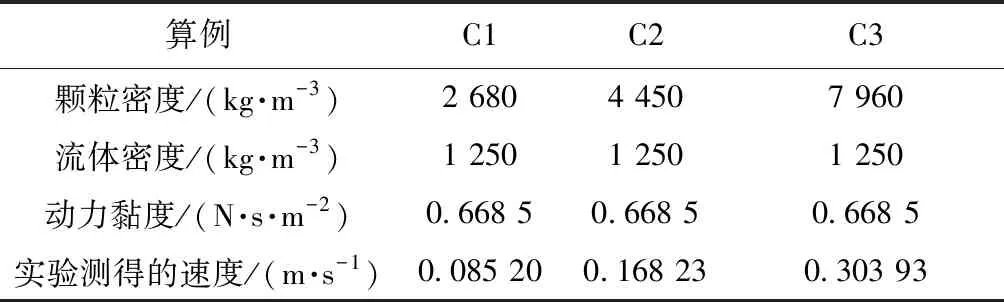
表3 实验和仿真参数Table 3 Experimental and simulation parameters
计算域设置为100 mm×100 mm×400 mm,其高度足够保证颗粒能达到稳态速度且不会碰到底部,网格数为40×40×160。颗粒的起始位置在计算域的中心线上,以避免旋转运动。颗粒尺寸为8 mm×8 mm×8 mm,其体积相当于直径为9.93 mm的球体。使用615个直径为1 mm的小球黏结成该正方体大颗粒,黏结参数同上。
图5显示了颗粒沉降速度曲线,可见仿真结果的最大值与实验结果吻合良好。与球体的沉降运动类似,立方体颗粒的速度在沉降过程中逐渐增加,直到达到稳态为止。图6为算例C2中密度为4 450 kg/m3的颗粒达到稳态时流场速度等高线图。结果表明本文提出的新方法可成功模拟IBM等解析CFD-DEM方法难以实现的三维情况下非球形大颗粒在流体中的耦合运动。
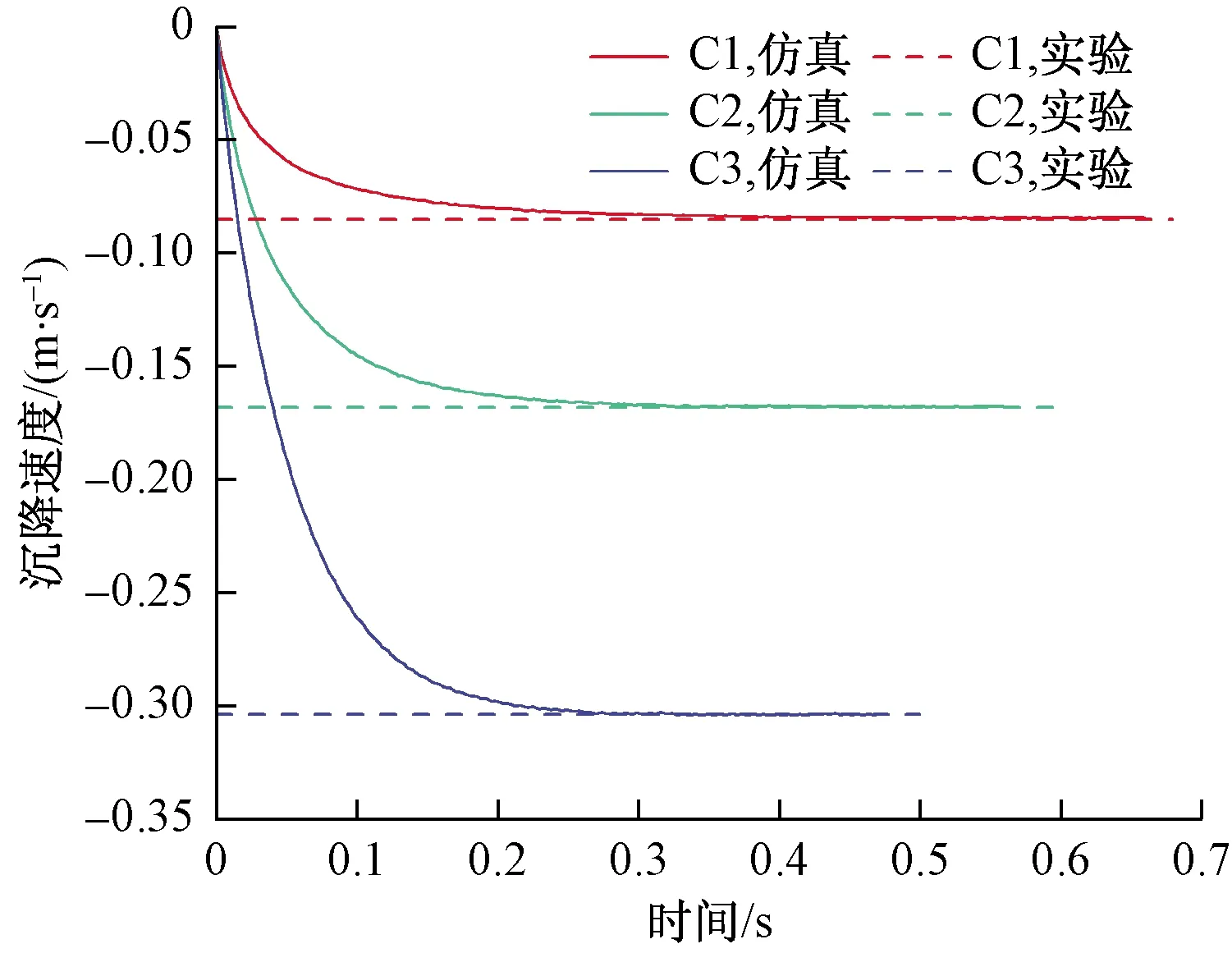
图5 颗粒沉降速度曲线与实验测量值的比较Fig.5 Comparison of the simulated particle settling velocities curves with the experimental values
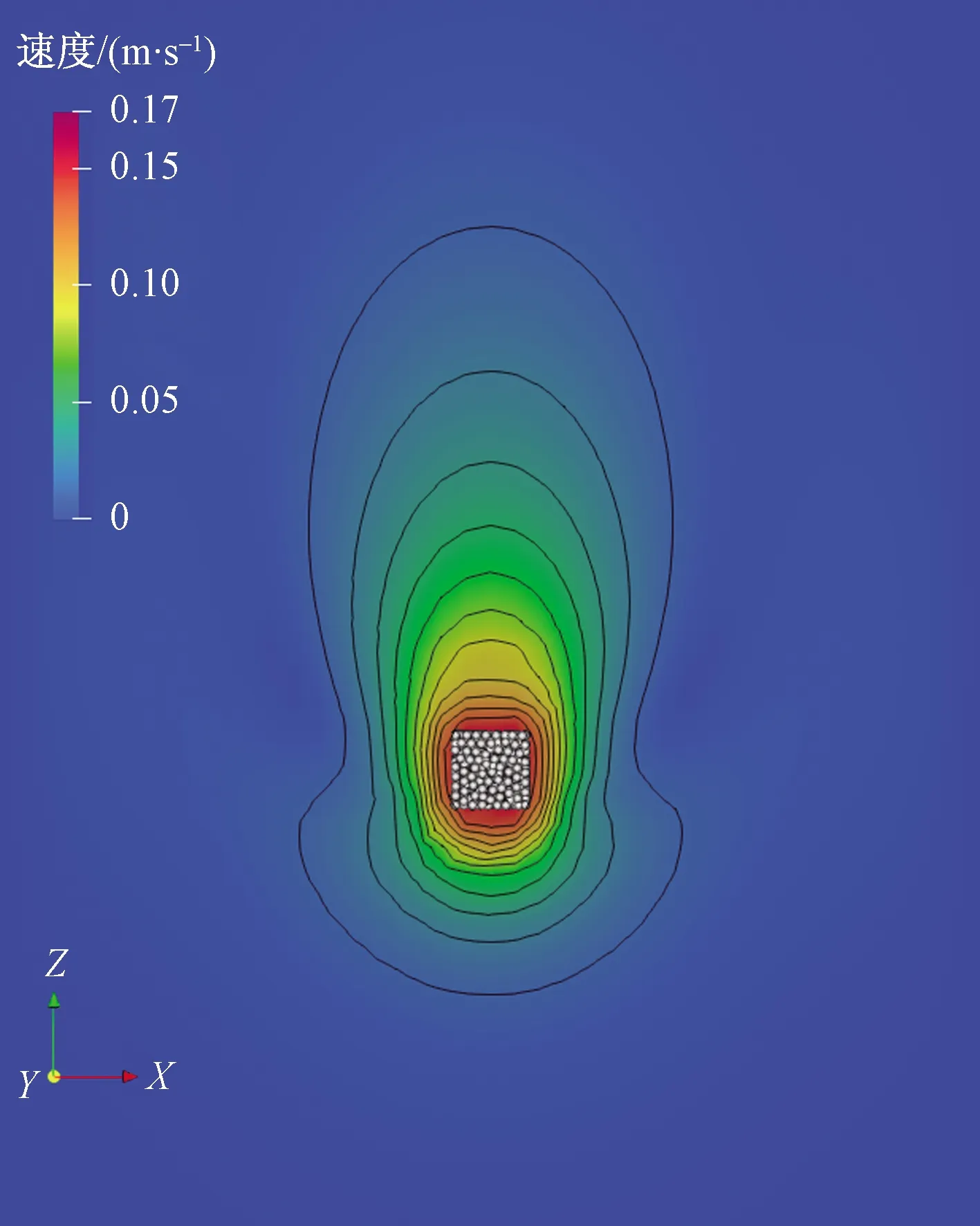
图6 算例C2的流场速度等高线图Fig.6 Contour map of flow field velocity of case C2
3.2 椭球形大颗粒沉降
为了验证该方法适用于可旋转的非球形大颗粒,进一步使用非解析CFD-DEM方法结合BPM模拟了三维情况下单个椭球形大颗粒在充满黏性流体的细长竖直管中的沉降运动。椭球的长轴长23.8 mm,两短轴长11.9 mm,其体积约等于直径为15 mm的球体。椭球颗粒通过黏结610个直径为1.5 mm的小球而形成,黏结参数同上。颗粒和流体密度分别为1 100 kg/m3和1 000 kg/m3;流体动力黏度为0.1 N·s/m2;计算域为95.2 mm×95.2 mm×1 800 mm,网格数量为18×18×360。椭球颗粒最初重心位于计算域的中轴线,长轴沿水平方向倾斜45°。
图7显示了四个时刻的颗粒运动位置和流场速度分布,其运动过程与Xia等[17]模拟的结果类似:开始时,椭球颗粒缓慢下落并逆时针摆动,逐渐靠近右壁面;然后,粒子摆动到长轴水平状态,但是它有继续转动的趋势。接着颗粒继续下降并逆时针摆动,并逐渐接近左壁面,且随着沉降过程摆动幅度逐渐减小至稳定的水平状态。
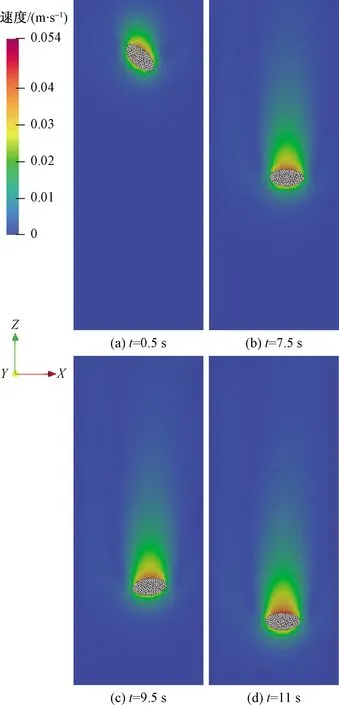
图7 不同时刻椭球粒子的位置和流场速度云图Fig.7 The position of the ellipsoidal particle and the flow field velocity contours at different time
4 结论
为高效率分析大颗粒在流场中的运动响应,提出将非解析CFD-DEM与BPM结合的方法,并通过大颗粒在流体中的沉降运动仿真分析进行计算精度和效率的评价,研究结论如下。
(1)仿真与实验结果的对比分析表明,使用非解析CFD-DEM方法结合BPM可较准确地模拟球形大颗粒在流体中的沉降运动,且计算效率显著高于IBM方法。
(2)非解析CFD-DEM与BPM结合的方法可有效模拟三维情况下非球形大颗粒在流体中包括平动和转动的沉降运动,使非球形大颗粒在流场中的高效率运动响应分析成为可能。

