基于改进果蝇的混合小波神经网络交通流预测
宋瑞蓉, 王斌君*, 仝 鑫, 刘文懋
(1.中国人民公安大学 信息技术与网络安全学院, 北京 100038; 2.绿盟科技集团股份有限公司, 北京 100089)
当今社会,随着汽车占有量的爆炸式增长,交通拥堵成了困扰中国乃至世界的重大课题。在人们对于便捷出行要求日益增强与道路交通压力逐渐增大的冲突之下,智能交通系统得到了极大的促进与发展。精准的交通流量预测是完善智能交通系统的重点和难点研究技术之一。交通流量预测是指通过对已有观测数据规律的研究,预测未来时刻的交通流量,从而便于人们进行出行选择和计划,同时也有利于交通管理部门对路面交通开展科学地统一调度、调配和管理。
现有文献对交通数据预测展开了广泛地研究,大致可分为以下五类:线性理论模型、智能理论模型、交通仿真模型、组合理论模型和非线性理论模型[1]。线性理论模型是利用线性的数学关系完成时间序列的递推。其中,最常见的为差分整合移动平均自回归模型(autoregressive integrated moving average model,ARIMA),该方法在早期交通预测中被大量使用。Liu等[2]将ARIMA作为组合模型长期短期记忆神经网络和时间序列自回归综合移动平均模型的组成部分对交通流进行预测,相较于单一模型提高了预测精度。卡尔曼滤波是最近应用较为广泛的线性理论模型,最初应用于系统状态估计,现在经常被用于时间序列数据的预测。周晓等[3]使用卡尔曼滤波对道路平均速度进行预测,同时考虑了该路段上下游车辆的平均速度因素,使得模型能够同时提取和关注数据的时间和空间特征。智能模型以神经网络模型为主,以其对数据拟合能力强且能够关注到数据间复杂的依赖关系而被广泛适用于各种领域。Ran等[4]使用卷积神经网络进行交通时间预测,同时提出了一种新的局部接受域,用来限制历史数据与待预测信息间的依赖关系,并结合注意力机制对卷积之后的结果进行自适应关注,增强模型对特征的提取能力。文献[5]将长短期记忆网络与注意力机制相结合对交通时间进行预测,与其他基线方法相比,该模型表现出了更好的预测能力。常见的交通仿真模型有自动分配理论、元胞自动机模型[1]。文献[6]中应用元胞自动机模型对航道内区域的船舶交通流进行预测建模,使用概率模型对航道外区域进行建模,从而完成对港口水域的交通流预测。交通数据中存在复杂的线性和非线性关系,所以单一模型往往无法提取到交通数据的全部特征,组合模型是通常采用的策略。文献[7]提出了基于CNN-ResNet-LSTM的网络结构,综合不同网络的优势,卷积神经网络(convolution neural network, CNN)提取空间特征,长短期记忆(long short-term memory,LSTM)网络提取时间特征,残差单元ResNet用于加深网络深度,提高了网络的特征提取能力。Liu等[8]建立了基于(LSTM)网络和人工神经网络(artificial neural network,ANN)的混合神经网络,将时间特征与空间特征相融合,并建立时间滚动窗完成数据的更新和遗忘,从而对公交车到达时间进行有效的预测。文献[9]使用LSTM网络将天气因素考虑在内从而对交通流做出更准确的预测。文献[10]提出了组合模型S-GCN-GRU-NN以预测短期交通流速度。其中,使用时空图卷积网络(spatiotemporal graph convolutional network,S-GCN)模型来获取复杂的时空相关性,并将门控回归单元神经网络(gated recurrent units-neural network,GRU-NN)模型用于短期交通速度预测。综上可以看出,组合模型是当前研究的热点方向,由于其可以综合不同模型优势,提取到更加全面的特征,从而被广泛应用。
智能优化算法是一种用来寻找目标函数全局最优值的方法,现常与深度学习网络相结合,能达到对网络模型的初始参数进行调优的效果。在果蝇优化算法、狼群算法、灰狼优化算法、蝴蝶算法等常见的智能优化算法中,果蝇算法(fruit fly optimization algorithm,FOA)表现突出,该算法于2011年由Pan[11]提出,模拟果蝇的觅食行为,从而寻找全局的最优解。文献[12]对果蝇算法进行了优化并用于交通流量预测,首先采用并行搜索策略和均匀交叉算子,提高了搜索范围和群间的通信能力。同时,提出了果蝇源分配策略来计算每群在下一次迭代中产生的果蝇数量。文献[13]为了克服基本果蝇优化算法的缺点,采用了免疫算法的自非自抗原识别机制和免疫系统的学习-记忆-遗忘知识处理机制,提高了果蝇优化算法的稳定性。文献[14]将果蝇算法中向优势个体聚集改进为向优势群体聚集,同时对聚集方法和搜索半径进行了优化。张铸等[15]提出了一种新型混沌步长果蝇优化算法,改进了果蝇算法中固定步长的缺陷。李春等[16]对搜索半径进行了动态优化改进,同时在适应度函数中增加了逃脱系数,提高了果蝇算法的局部和全局搜索能力。
选择适合于时序数据特征提取的小波神经网络进行交通流量预测,并使用果蝇算法对小波神经网络中的大量初始参数进行调参处理,解决了初值敏感问题。同时,对果蝇算法进行了改进,在保证搜索精度的同时提高搜索效率。此外,采取了组合模型的思路进行了误差二次提取,弥补了单一模型无法提取到数据间的复杂关系,从而导致预测精度不高的缺陷。下面分别进行阐述,与读者商榷。
1 相关工作
为了清晰地阐述本文对小波神经网络预测模型的改进,下面先对已有小波神经网络和果蝇优化算法的核心内容进行简要地表述。
1.1 小波神经网络
交通流量数据中隐含着复杂的非线性关系,神经网络对于这种复杂关系具有很好的提取能力。小波神经网络(wavelet neural network,WNN)在人工神经网络的基础上结合了小波变换技术,激活函数采用小波基函数,输出层对所选取的小波基函数进行加权求和。相较于BP(back propagation)神经网络而言,小波神经网络能够简化网络的训练,在时序数据预测方面往往表现更加突出。
小波神经网络隐含层的输出表示为
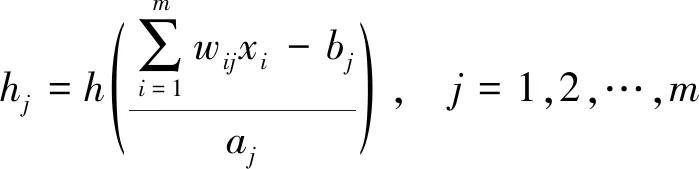
(1)
式(1)中:h(x)为隐含层所选取的小波基函数;wij为输入层与隐含层之间的权重系数;aj为小波基函数的伸缩因子;bj为平移因子;hj为隐含层神经元的输出。
小波神经网络输出层的计算公式为
(2)
式(2)中:wjk为隐含层与输出层之间的权重系数;yk为小波神经网络的输出值。
式(1)、式(2)中的权重参数wij和wjk、小波伸缩因子aj以及小波平移因子bj均采用误差反向传播,通过梯度下降的方法不断迭代更新得到,但初始值需要在模型训练前进行设定。小波神经网络对参数的初始值较为敏感,所以采用果蝇算法对小波神经网络的初始参数进行调节,以提高模型的效率和预测能力。
1.2 果蝇优化算法
果蝇优化算法模拟生物界中果蝇的觅食行为,可用于寻找全局最优解。首先初始化果蝇种群,让果蝇的初始位置在整个空间中随机分布,并确定距离食物最近的果蝇位置,其他果蝇依据视觉向该果蝇方向移动,从而使整个种群向食物所在的位置靠近。果蝇算法的优点在于运行速率快、简单易懂并且有很好的收敛性能和全局搜索能力。
步骤一初始化果蝇种群。
首先,初始化果蝇种群数量sizepop、最大迭代次数maxgen以及果蝇位置(X,Y)。果蝇的初始位置采用随机初始化进行赋值。
文中所优化的参数为权重系数wij和wjk、小波伸缩因子aj及平移因子bj。需要优化的参数数量N的计算公式为
N=inputnum·hiddennum+2·hiddennum+
hiddennum·outputnum
(3)
式(3)中:inputnum代表网络输入神经元的个数,hiddennum代表隐含层神经原个数;outputnum代表网络输出神经元个数。
步骤二果蝇依嗅觉进行搜索。
为果蝇赋予随机的搜索方向与范围,表达式为
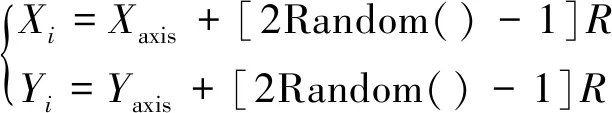
(4)
式(4)中:R代表搜索半径。
步骤三计算位置浓度判定值Si。
根据果蝇的位置来判断其与食物之间的距离,但由于无法获取食物的坐标,将果蝇与原点之间距离的倒数作为浓度判定值Si,表达式为
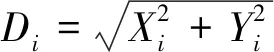
(5)

(6)
步骤四将步骤三所求出的浓度判定值Si代入浓度判定函数,即该问题中的目标函数,求出不同位置的果蝇所对应的气味浓度,从中选取具有最佳气味浓度的果蝇,计算式为
(bestSmell,bestIndex)=min[f(Si)]
(7)
式(7)中:bestSmell为本次迭代后最优的气味浓度;bestIndex为该气味浓度所对应的索引。文中所选取的浓度判定函数为绝对值误差,表达式见式(8)所示。

(8)
步骤五将具有最佳浓度的果蝇所在位置设置为本次迭代之后的最佳位置,其他果蝇向该果蝇的位置靠近。
Xaxis=X(bestIndex)
(9)
Yaxis=Y(bestIndex)
(10)
步骤六重复执行上述步骤,若最佳浓度优于上次迭代后的最佳浓度时,执行式(9)、式(10),更新最佳位置,直到达到最大迭代次数。
2 基于改进果蝇优化算法的混合小波神经网络预测模型
2.1 模型总体结构
基于改进果蝇的混合小波神经网络预测模型由三部分组成,分别为改进的果蝇算法、小波神经网络以及用于误差二次提取的组合模型。具体模型结构如图1所示。

图1 基于改进果蝇的混合小波神经网络预测模型Fig. 1 Hybrid wavelet neural network prediction model based on improved fruit fly optimization algorithm
步骤一利用改进的果蝇算法搜索初始权重参数和初始小波因子。
步骤二将改进果蝇算法输出值作为小波神经网络的初始参数,投入训练数据后,开始进行模型训练,输出预测值及误差序列。
步骤三将步骤二提取的误差序列输入用于误差提取的组合模型中进行训练,输出误差预测值。
步骤四将步骤二输出的模型预测序列与步骤三输出的误差预测序列叠加,得到经过误差二次提取后的最终预测结果。
2.2 果蝇优化算法的改进
2.2.1 搜索半径改进
果蝇优化算法中的搜索半径R对搜索结果具有重要影响,搜索半径较大时,有利于进行全局搜索,但会使训练后期的局部收敛速度下降;半径较小时,在搜索后期有利于寻找最优值,但在前期容易陷入局部最优。基本果蝇算法中搜索半径为固定值,这会降低搜索的效率,将搜索半径动态化可以解决搜索前后期对于搜索半径的不同需求。
文献[17]中提出了改进的DS-FOA算法,将迭代次数对于搜索半径的影响予以考虑,在迭代前期,需要进行全局搜索,搜索半径较大,到迭代后期,已基本靠近最优值,此时需要缩小搜索半径,从而通过迭代次数对搜索半径加以调整,搜索半径公式为
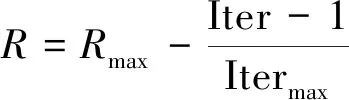
(11)
式(11)中:Rmax表示最大搜索半径;Iter表示现在已完成的迭代次数;Itermax代表初始化的最大迭代次数。
式(11)动态化搜索半径,使得搜索半径随迭代次数增加而减小,但也存在一定问题,由于搜索半径与迭代次数呈一次线性关系,搜索半径的下降速度保持恒定,使得在迭代初期搜索半径的下降速度较快。文献[16]对就针对该缺陷进行了改进,让搜索半径在迭代初期保持恒定,在经过一定迭代次数之后开始减小,具体表达式为

(12)
通过设置搜索半径的衰减因子μ使搜索半径在迭代初期保持稳定,经过一定迭代次数后,搜索半径才开始下降,从而解决了上述问题。由于衰减因子μ需要人为设定,且不同μ的取值会对结果造成影响。本文对该方法进行改进,使得搜索半径在迭代初期可以缓慢下降,在迭代后期快速下降,从而动态调整搜索半径的减小速率,改进后的搜索半径表达式为
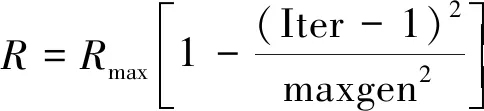
(13)
改进后的搜索半径与迭代次数呈二次关系,迭代初期搜索半径变化程度较小,使得搜索半径基本保持稳定;迭代后期半径减小加快,由于此时已接近最优值,减小搜索范围更有利于寻优。
搜索半径的变化不仅需要考虑迭代次数,还需考虑当前局部的最优解,若当前局部最优解较差时,需要增大搜索半径,反之,则需减小搜索半径。文献[18]对局部最优解的取值进行考虑,并依此对搜索半径进行了改进,表达式为
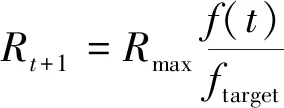
(14)
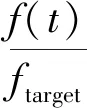
在实际问题中,某些情况下无法获知目标最优值,所以对式(14)进行了改进,引入当前局部最优值bestSmell与上次迭代所产生的气味浓度值f(t),用两者比值作为搜索半径的调整因子,具体表示为
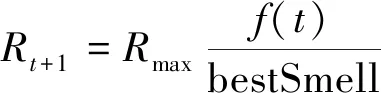
(15)
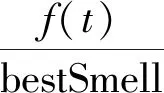
现有动态搜索半径的方法中只单一将迭代次数作为调整因子或将当前浓度函数的取值作为调整因子,将改进后的两种方法进行结合,表示为

(16)
将式(16)代入式(4)中就得到更新之后的果蝇位置,即

(17)
2.2.2 种群数量改进
文献[18]中引入了可变种群规模策略,种群数量会随当前函数取值与目标值的比值而发生变化,表达式为
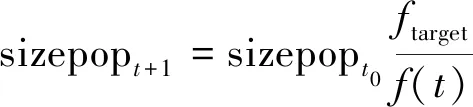
(18)

本模型所选取的气味函数是将归一化后的数据经模型训练所得到的预测值与真实值之间的绝对值误差,气味浓度取值较小,式(18)会造成种群数量变化范围过大,当种群数量取值过大时,会造成算法效率下降,取值过小时则达不到调参的效果。对式(18)进行改进,改进之后的种群数量变化公式为
sizepopt+1=sizepopt0ebestSmell-f(t)
(19)
式(19)中:Smellbest代表当前局部最优值,f(t)代表第t次迭代后气味浓度的取值,Smellbest-f(t)>0时表示当前的解优于局部最优解,则增加搜索能力,扩大种群规模,反之,当前解较差,减小种群规模。
为了对比两种方法下种群规模的变化范围,以AL1053路段为例,将调参过程中种群数量的变化过程分别进行统计。其中,式(18)所代表的种群数量变化公式记为比值法,改进后式(19)所代表的方法记为指数法,两种方法的实验结果如图2所示。
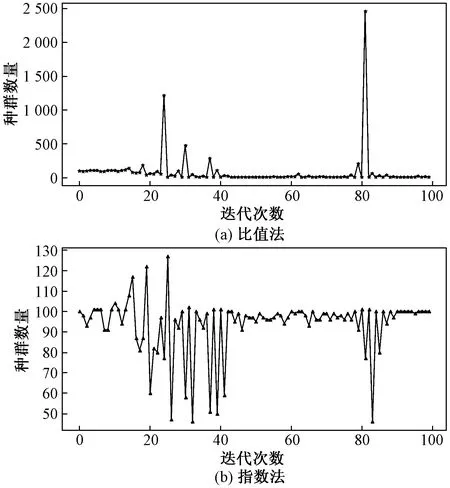
图2 比值法与指数法种群数量变化对比Fig.2 Comparison of population change between ratio method and index method
由图2可以看出比值法的种群数量变化范围为(0,2 500),当前解较差时,种群数量会降低至个位数,此时,达不到调参的效果;当前解较好时,种群数量会有大幅度增加,此时,会降低算法的运行效率。改进后的指数法种群数量变化范围为(40,130),变化范围较小,种群数量可以保持在合理的预期区间内,可以在保证算法运行效率的同时达到调参的效果。
2.3 误差二次提取
误差补偿法(error compensation,EC)是提取预测模型的误差后,再次对误差进行训练,得到误差的预测值,然后将预测值序列与误差值序列相叠加,从而得到最终的预测结果[19]。
文献[19]中提到,交通流预测实验中所得到的误差通常具有某种规律性,再次使用同一模型进行误差二次提取可以挖掘到误差中所隐含的特征信息。文献[20]将船舶的交通流量数据分为线性和非线性两部分,采用误差补偿法组合SARIMA模型与BP神经网络模型,分别用于提取交通流数据中的线性和非线性成分。
将小波神经网络作为第一个误差提取模型,分别与小波神经网络(WNN)、长短期记忆人工神经网络(LSTM)、双向长短期记忆人工神经网络(BiLSTM)、极端梯度提升模型(eXtreme gradient boosting,XGBoost)、随机森林模型(random forest,RF)使用误差补偿法进行组合。使用小波神经网络对自身预测的误差进行二次提取,如文献[19]中所述,可以提取误差中的隐含特征。长短期记忆人工神经网络与双向长短期记忆人工神经网络擅长处理时序化数据,与小波神经网络组合进行误差二次提取能够提取到隐含的时序特征。极端梯度提升模型和随机森林模型与小波神经网络结构相差较大,与小波神经网络组合能够增强预测模型的互补特征提取能力。误差二次提取的具体模型结构如图3所示。

图3 误差二次提取组合模型Fig.3 Error secondary extraction combination model
3 实验结果
3.1 交通流数据及其预处理
实验数据由英国公路局提供和管理。实验中共选取了10个数据集,分别是道路AL1053、AL1249、AL1251等在2014年1月份上的交通流量数据。实验数据是通过传感器等方式获得,所以存在一定的噪声,为了使模型预测更加准确,首先应对数据进行降噪处理。
交通流量数据中存在的噪声通常为高频信号,可以采用小波变换的方法对数据进行降噪处理。本文采用db4小波对交通流量数据进行了4层分解,将含有噪声的高频系数提出,重构小波分解向量,将其中的第一、二层细节分量置零,得到降噪处理之后的交通流量序列。经过降噪处理后的数据序列仍能保留原数据序列的相关趋势,但可以使得整个序列变得更加平滑,去除测量时的不精确及其他噪声原因造成的误差。
采用三层网络结构的小波神经网络,输入层、隐含层及输出层的神经元个数设置为4、6、1。为权重系数和小波因子设置了不同的学习速率,分别为0.01和0.001。小波基函数为Morlet小波,表达式为

(20)
实验结果评价用到3个误差指标分别为均方根误差RMSE、平均绝对误差MAE及平均绝对百分比误差MAPE,计算公式为
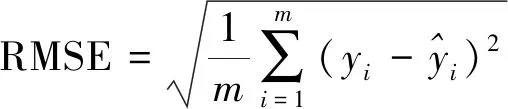
(21)
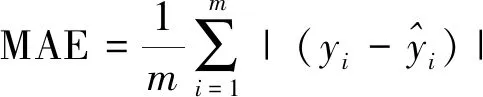
(22)
(23)
3.2 改进果蝇算法实验结果
使用小波神经网络(WNN)、经果蝇算法调参的小波神经网络(FOA_WNN)和本文提出的经改进后的果蝇算法调参的小波神经网络(FOAC_WNN)3个模型分别在所选的10条不同路段的交通流量数据集上进行实验,用上述误差评价指标对实验结果进行评价,如表1所示。
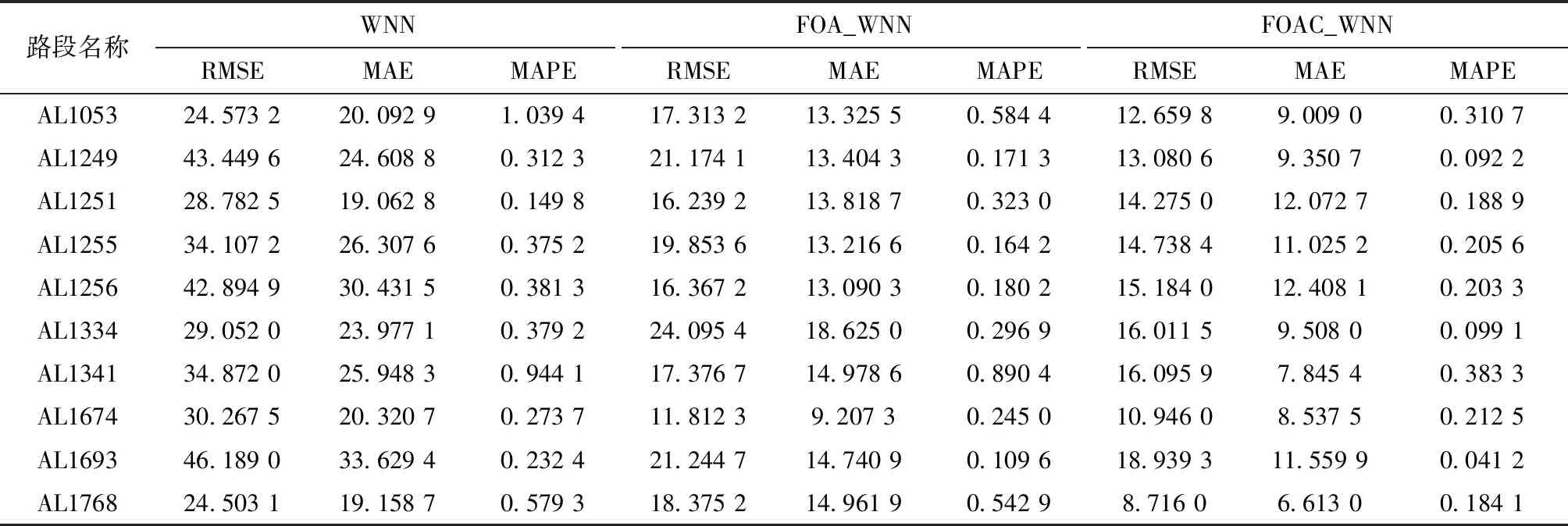
表1 使用改进果蝇算法调参的实验结果对比Table 1 Comparison of experimental results using improved fruit fly optimization algorithm
由表1可以看出FOAC_WNN在3种误差评价指标下均表现出了更好的预测能力。为了更清楚地显示FOAC_WNN模型对特殊点交通流量预测的优势,现对交通流量的峰值与低谷值进行观察,3种模型的对比预测效果如图4所示。
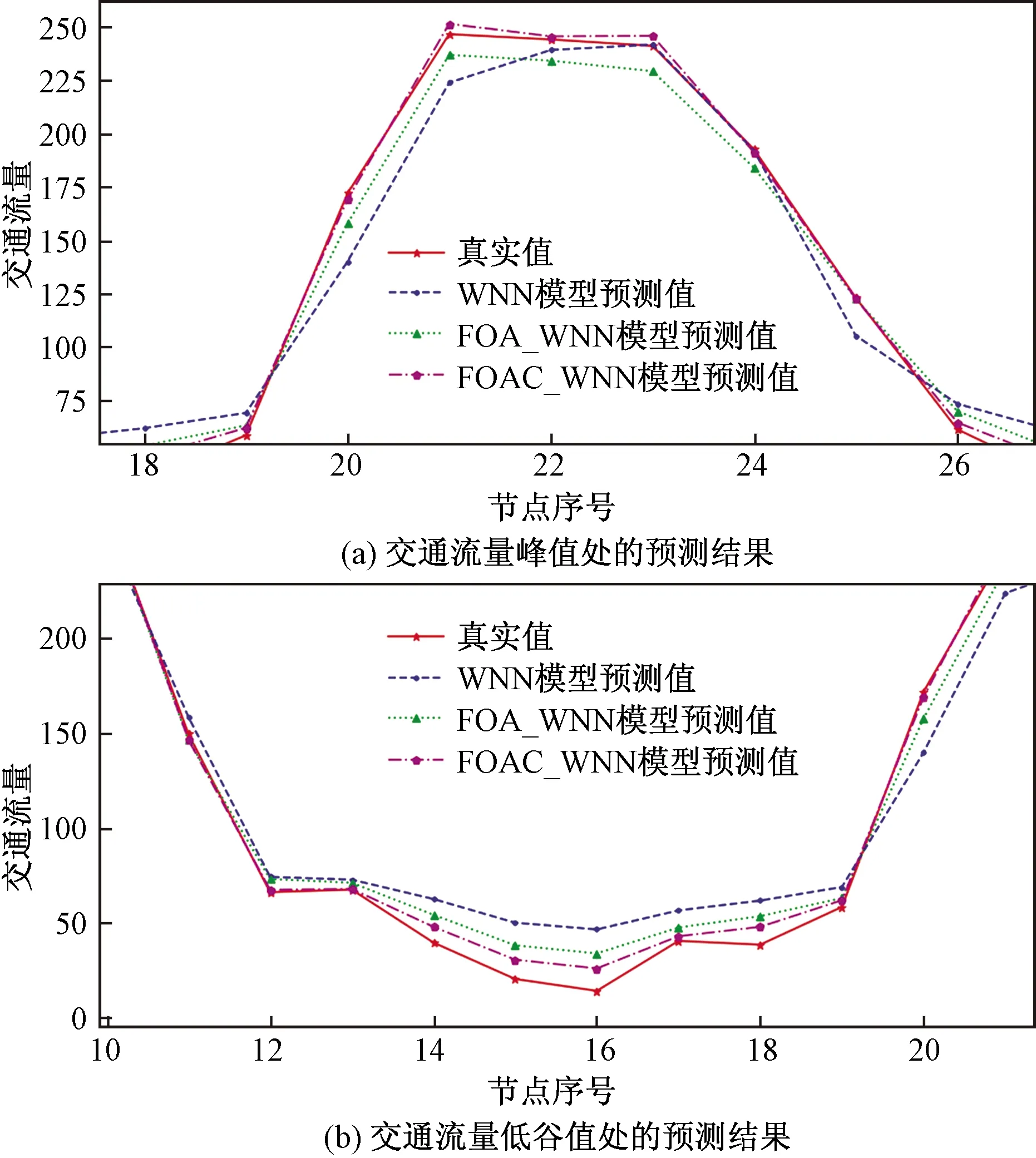
图4 交通流量峰值与低估值处的预测结果Fig.4 Prediction results at peak and underestimation of traffic flow
由图4可以看出,经改进的果蝇算法调参后的小波神经网络在交通流量峰值处和低谷值处预测效果均优于其他两种模型,说明该模型能够拟合各种时间点下的交通流量变化趋势,并且能够做出较为精准的预测。
为了观察这3种模型在所有数据集上预测误差的离散情况,将结果的MAPE指标绘制为箱线图,如图5所示。
由图5可以看出FOAC_WNN的MAPE指标的中位数、四分位数、上边缘均低于其他两个模型,同时预测误差更为集中,说明该模型在不同数据集上的预测效果更加稳定,且均优于其他两个模型。
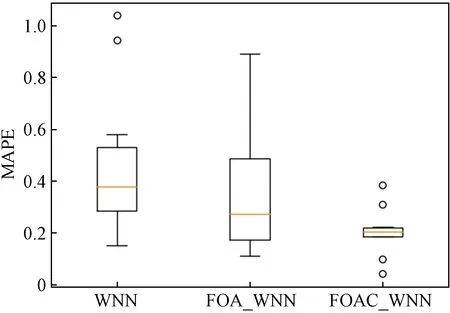
图5 不同模型MAPE箱线图对比Fig.5 Comparison of MAPE box diagram of different models
3.3 组合模型实验结果
为了进一步提高模型预测的准确度,使用前文所述的误差补偿法将经过改进后果蝇算法调参的小波神经网络(FOAC_WNN)与其他模型相结合,这些模型分别为小波神经网络(WNN)、长短期记忆人工神经网络(LSTM)、双向长短期记忆人工神经网络(BiLSTM)、极端梯度提升模型(XGBoost)以及随机森林 (random forest,RF) 模型,使用3种评价指标对实验结果进行评价,如表2所示。
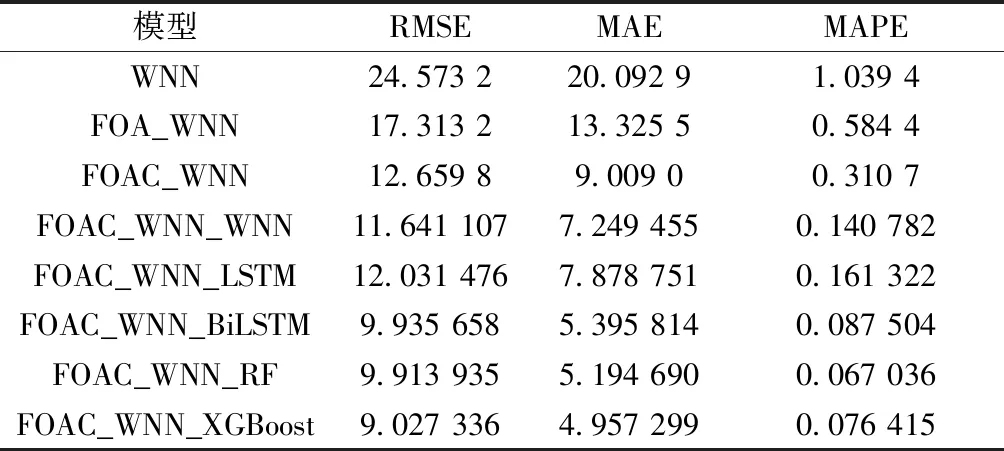
表2 组合模型预测结果
由表2可以看出经过误差二次提取,模型的预测准确度均有提高,其中与Bilstm模型、RF模型、XGBoost模型相结合的组合模型预测效果明显优于其他模型。具体而言,与XGBoost模型相结合的组合模型在RMSE、MAE指标上表现最优,与RF模型相结合的组合模型在MAPE指标上表现最优。综上而言,这两种模型在3种误差指标上相差较小,均可以使用误差倒排法与经改进果蝇算法调参的小波神经网络相结合作为交通流量预测的二次误差提取最佳模型。
4 结论
选用小波神经网络对交通流量进行预测。由于小波神经网络对初始权重和小波因子敏感,故选用果蝇优化算法对权重参数和小波因子的初始值进行调节,并且从搜索半径和种群数量两个方面对基本果蝇算法进行了改进。实验证明使用改进后的果蝇算法对小波神经网络进行参数调节,提高了模型的预测准确度和收敛速度。另外,考虑到交通流量数据中蕴含着复杂的线性和非线性关系,以及小波神经网络预测误差蕴含的规律性,进而采用误差补偿法与小波神经网络、长短期记忆人工神经网络、双向长短期记忆人工神经网络、极端梯度提升模型以及随机森林模型进行组合,进行误差的二次提取与补偿修正。通过实验证明,组合模型均能够提高模型的预测准确度,其中随机森林模型与经改进果蝇算法调参的小波神经网络相组合表现出最好的预测效果。
文中只考虑了交通流量的时间特征,尚未考虑空间特征。将时空特征进行融合提取交通流量信息是接下来需要重点进行研究的内容。

