获取俯仰信息的车载合成孔径雷达成像方法

蒋留兵, 汪 林, 车 俐

(桂林电子科技大学计算机与信息安全学院，桂林 541004)

毫米波雷达作为自动驾驶三大重要的传感器之一，拥有独特的感知优势和极强的环境适应能力。相比较于激光雷达和摄像头[1]，毫米波雷达具有探测距离远、测速精度高以及可实现穿透检测等优点，同时在光线环境较差和风沙雨雪恶劣天气下表现出更可靠的感知水平[2]。但现有的车载毫米波雷达系统也存在一些不足，主要表现在目标分辨能力较差，目标信息不直观等。

现有体制车载雷达其分辨率能力由相应维度的阵列实孔径大小决定，在满足天线排布间隔的条件下，较大孔径就意味着更多的天线和射频通道，同时也会提高系统成本和处理复杂度，丧失其体积小、功耗低的优势。针对这一问题，不少学者和公司将最早发展于机载星载的合成孔径雷达成像技术应用于车载雷达上，利用车辆行进轨迹形成大孔径，提高目标水平方向的分辨率。早在2006年Wu等[3]将合成孔径雷达(synthetic aperture radar，SAR)技术中的距离徙动算法(range migration algorithm，RMA)应用于车载场景并进行了仿真验证。Yamada等[4]通过实测实验对比实孔径角雷达在使用SAR技术前后的检测效果，证明使用SAR技术能更清晰地分辨目标。文献[5]将77 GHz贴片雷达安装在一个线性轨道上模拟车载SAR，使用距离多普勒算法对车辆尾部成像，并分析导轨在不同速度下的成像质量。Feger等[6]将雷达放在车辆的顶端，采用侧前方俯视的模式，通过车辆运动形成大孔径，对行进方向-距离维组成的二维区域成像。以上研究表明车载合成孔径技术的有效性。但所获得的图像相较于真实目标存在不小差距难以令人满意，Iqbal等[7]进一步尝试将极化合成孔径雷达(polarimetric SAR，PolSAR)应用在车载场景中，以增加目标的多极化信息，该方案相较于单极化具有更清晰的效果，但其同样使用一维合成孔径的方案，没有从本质上解决不能获得目标俯仰信息的问题，为后续目标的识别分类工作带来困难。

基于前人研究，首次提出将一维车载合成孔径阵列扩展到二维的车载SAR成像方案，利用等效均匀阵列提供俯仰方向上的分辨能力，并通过车辆移动形成大孔径以提供水平方向高分辨率，使其能够有效反映目标的真实外形信息。采用线性导轨和商用毫米波雷达搭建数据采集系统，对车辆直线运动场景进行模拟，以研究二维SAR方案的可行性。同时进一步考虑所提二维SAR成像方案在车辆非直线运动情况下的算法，传统后向投影算法在该方案和场景下依然适用，但存在时间复杂度过高的问题，结合方案中的阵元位置特点，对该二维方案在非直线运动场景下的快速成像算法进行研究。

1 模型介绍

1.1 回波信号模型

采用调频连续波(frequency modulated continuous wave，FMCW)雷达中锯齿波信号模型进行成像算法和系统的研究。该体制雷达具有容易实现、结构相对简单、集成度高及成本低等优点，在民用领域尤其车载领域得到了广泛的应用[8]。下面对FMCW回波信号模型进行描述。发射和接收信号模型分别可以表示为

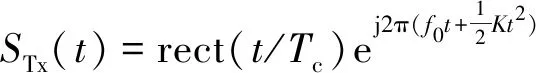
(1)

(2)

式中：rect()为矩形窗函数；Tc为脉冲重复周期；K为调频斜率；f0为起始频率；σi为目标区域第i散射点的反射系数，第i散射点到相位中心时延由τi=2Ri/c决定，Ri为第i散射点到相位中心的距离，c为光速。发射信号与接收信号混频得到中频信号，即

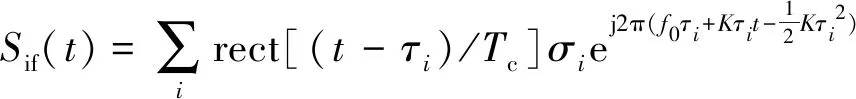
(3)

式(3)中：指数项的第三项为残留视频相位(residual video phase，RVP)项，因为目标距离相对较近，回波时延的二次方相对较小，在车载场景通常可以忽略[9]。将式(3)中频信号表达式进一步写为

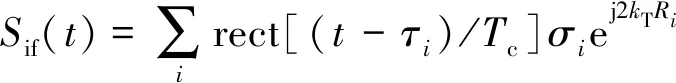
(4)

式(4)中：kT=2π(f0+Kt)/c。合成孔径雷达成像就是通过联合处理不同位置得到的中频回波信号，恢复出目标各散射点幅值信息。

1.2 直线运动场景成像几何模型

由合成孔径雷达的知识可知，雷达从波束扫描起始到波束扫描结束，所走过的路程为相应合成孔径的长度。同样在车载SAR成像中，通过车辆移动获得等效大孔径阵列。本方案中模型如图1所示，建立空间三维直角坐标系，以俯仰天线阵列中间位置作为原点，分别以车辆行进方向、空间俯仰方向和雷达径直辐射方向为X、Y、Z轴。雷达随车辆移动进行信号收发，由于脉冲持续时间Tr和电磁波传播所需时间τ都远小于脉冲重复间隔(pulse repetition interval，PRI)，在车速较慢情况，近似认为雷达在同一位置获得目标的反射回波，上述过程可以看作“走停走”的模式[10]。车辆以速度v行进，根据信号的脉冲重复周期Tc可计算水平采样点均匀间隔ΔX=vTc，当车速改变时通过相应改变Tc可以获得等间隔阵列，文献[11]中研究了在不同车速下得到对应脉冲重复频率的方法，通过调整发射信号参数可以达到水平方向均匀采样的数据，因此本文中仅研究匀速场景下的成像情况。在实际应用中，俯仰方向的均匀阵列数据获取，可由多片级联MIMO经过等效得到[12]。在直线运动场景下，最终能够根据等效均匀排布的二维面阵数据进行成像。

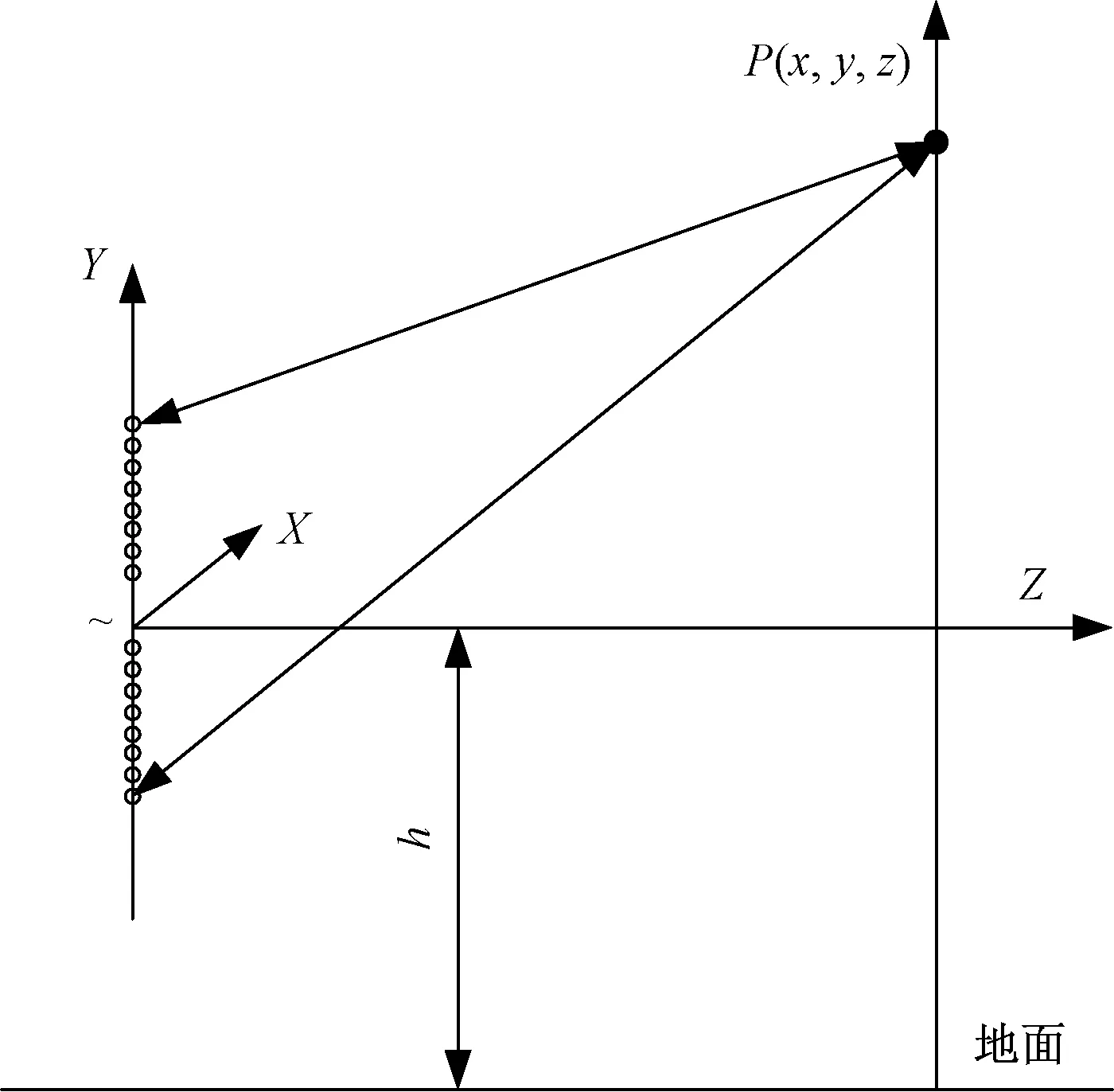
图1 二维SAR成像几何模型Fig.1 Two-dimensional SAR imaging geometric model

2 线性导轨数据采集系统搭建

为了验证方案的可行性，需要获取数据进行成像验证，而商用多片级联MIMO雷达未开放获取，根据现有设备，选用77 GHz商用MIMO雷达AWR1243和线性导轨搭建数据采集系统，通过MIMO等效和空间重复采样得到等效均匀阵列的数据。

该雷达设计有3发4收天线，选用其中处在同一直线上的2个发射天线和4个接收天线，当雷达工作在时分复用(time-division multiplexing，TDM)模式[13]，发射天线1和2先后发送FMCW信号，到达反射点后将携带目标散射系数的信号返回到接收天线。根据MIMO等效原理可以得到8个通道的数据，在此期间忽略由于传播路程的微小差异对信号带来的幅值影响。该系统中MIMO雷达等效相位中心为收发天线的中间位置，因此得到间隔λ/4(λ为波长)的8个收发同置的阵元，结果如图2所示。该系统所得等效虚拟阵列与商用多片级联MIMO等效虚拟阵列具有相同的阵元间隔λ/4，通过将该阵列竖直沿拖，能够得到和商用多片级联MIMO雷达相同的数据采集效果。

图2 MIMO天线阵元等效Fig.2 Equivalent elements of MIMO antenna

在某固定水平采样处，通过俯仰方向导轨移动和MIMO雷达的分时收发获取俯仰-距离维的二维数据，随水平方向采样不断积累最终得到三维的中频信号，其采集过程如图3所示。因此根据系统和信号模型，等效三维中频信号表示为

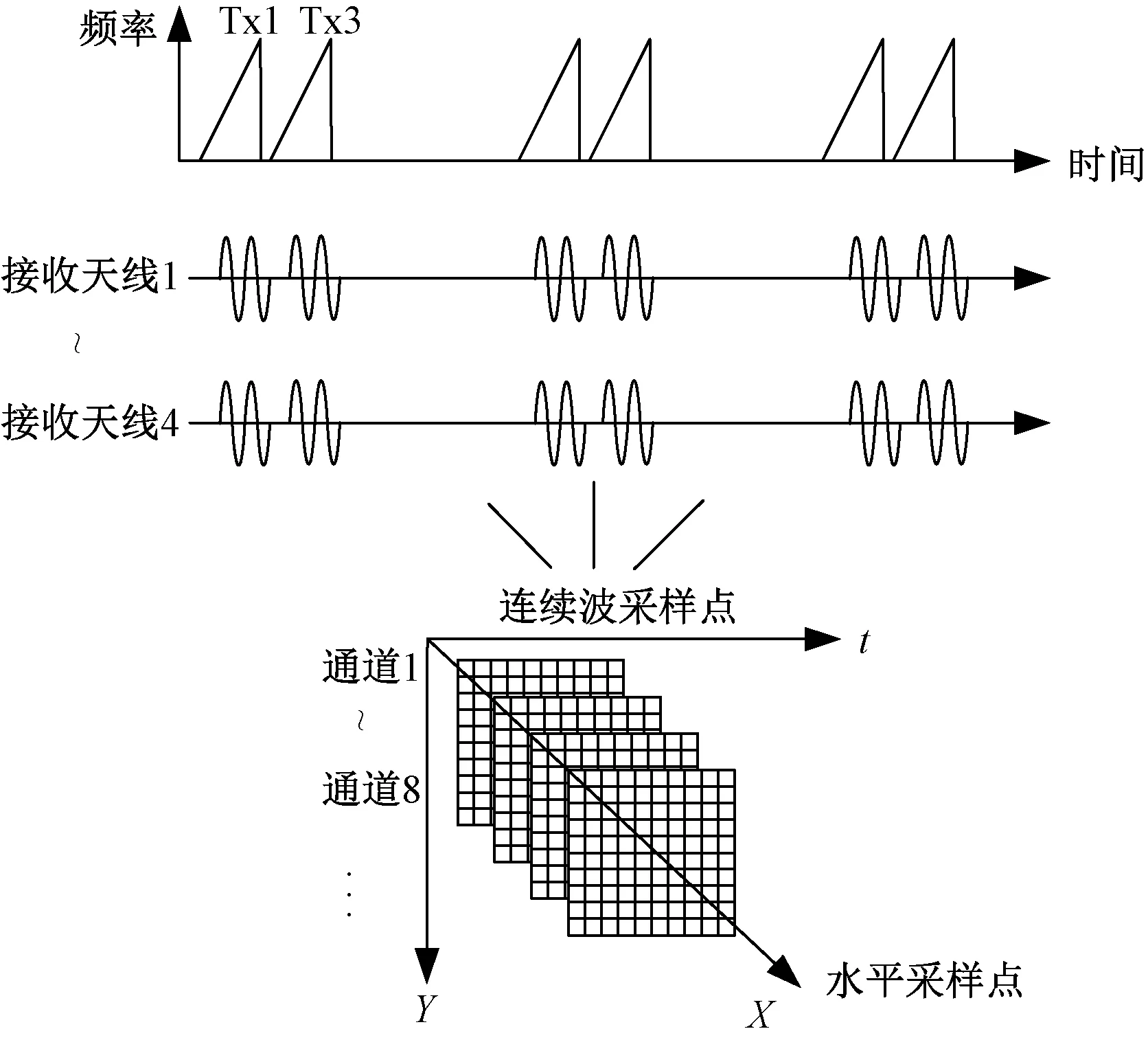
图3 数据采集过程Fig.3 Data acquisition process

(5)

式(5)中：X=(XTx+XRx)/2，Y=(YTx+YRx)/2为对应收发天线中间位置；τ(X,Y,i)=2R(X,Y,i)/c表示第i散射点到等效相位中心的时延。

3 直线运动场景实测数据成像分析

根据所搭建系统模拟车辆直线运动场景，对数据采集系统和二维车载SAR成像方案进行验证，分别在室内和室外进行了实测数据成像实验。在成像算法方面，采用二维匹配滤波算法进行成像，该算法广泛用于安检成像中[14]，要求天线阵列处在一个二维平面，且满足奈奎斯特空间采样定律。由上文分析，车辆直线轨迹下所得数据，经过处理后可等效为均匀排布的二维面阵数据，因此该算法适用于此场景。

首先进行了数据采集系统的室内数据采集测试。如图4(a)将刀片和光盘粘贴在泡沫板上，放置在距离雷达约1 m处的位置，截取对应距离单元的数据，使用该系统采集的数据进行成像效果如图4(b)所示，图像的动态范围设置为0～16 dB，可以看到对于目标有很好的重构效果。

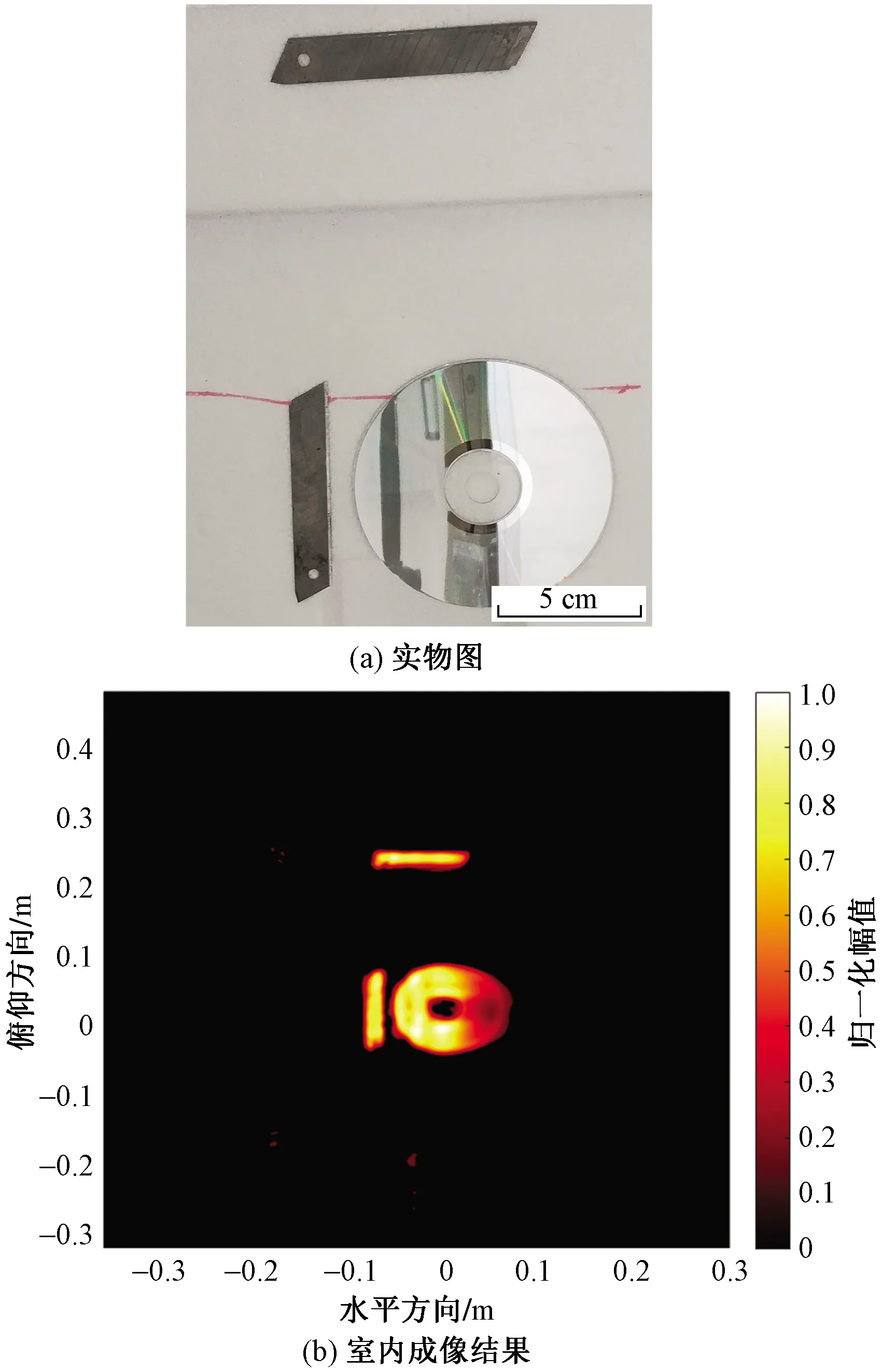
图4 室内实测结果Fig.4 Indoor measured results

室外测试中，将目标护栏放置在距离雷达3 m处，其中护栏的高度1 m，长度1.4 m，场景如图5(a)所示。首先使用一维SAR方案采集水平-距离维数据，将该二维矩阵通过补零得到三维矩阵，沿距离维变换到频域取对应距离单元的二维矩阵，进行二维匹配滤波成像，结果如图5(b)所示，图像中能够分辨六个竖杆，但没有出现上下两个横杆。实验表明，对于竖直摆放的目标，一维SAR方案虽然可以实现水平方向的分辨，却无法进行俯仰方向的重构。进一步进行二维SAR方案实验，获取水平-俯仰-距离维的三维数据，采用同样的步骤进行成像，结果如图5(c)所示，重构图像能够很好地还原目标外形轮廓。

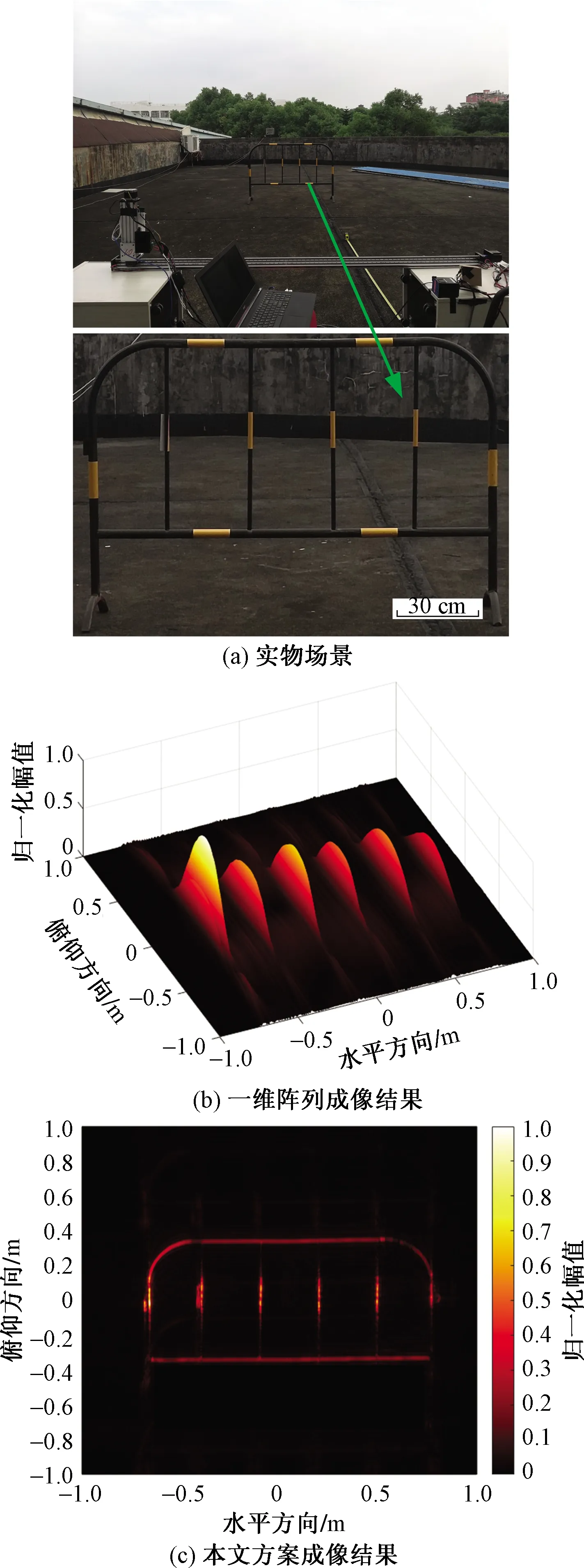
图5 外场实测结果Fig.5 Field measurement results

4 非直线二维SAR快速成像算法

由上节实测数据实验和分析可知，当车辆沿直线运动时，二维SAR成像方案可以达到预期成像效果。但车辆实际行驶过程中可能存在非直线轨迹运动情况，如图6所示。当车辆在沿X轴行进时，存在Z轴方向的偏移，考虑此时X轴方向仍是均匀等间隔采样，则天线阵列到第i散射点的距离可以表示为R[X,Y,Z(X);i]，对应中频信号为

图6 非直线轨迹成像几何模型Fig.6 Nonlinear trajectory imaging geometric model

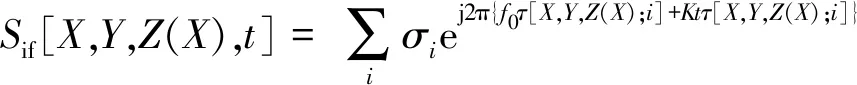
(6)

本节研究此场景下的快速成像算法，当采集信号的阵元不再处在同一平面时，原有可用于二维平面阵的算法都不在适用，非平面阵下只有BP算法可进行目标图像的重构。BP算法适用于满足任意轨迹下的成像，但计算时间复杂度过高[15-16]，并且没有充分利用该方案下阵元的特点。针对这一问题，提出一种非直线轨迹二维SAR快速成像算法。

4.1 理论分析与算法流程

根据式(6)，车辆非直线运动场景下成像模型表示为

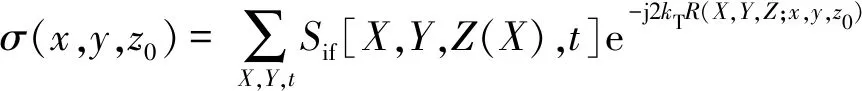
(7)

xq为第q列散射点水平坐标，当x为特定值xq时，有

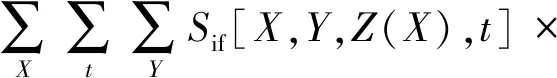
(8)

式(8)中：对于固定X的中频信号，是由俯仰方向和时间维组成的二维矩阵。将二维中频信号矩阵与二维匹配滤波矩阵点乘，然后沿Y方向累加，此过程可以等效为卷积形式，即

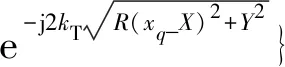
(9)

(10)

式(9)中：R(xq_X)表示水平坐标为xq的散射点到坐标X天线的径直距离。

根据信号处理知识，空域卷积可以由波数域相乘得到。此距离R[xq_X]下的匹配滤波函数变换到波数域为

(11)

FT和IFT分别表示傅里叶变换和傅里叶逆变换。因为IFT只与KY有关，与时间t无关，所以可以交换时域累加运算和IFT的顺序，进一步减少运算量。

σ(xq,y,z0)=

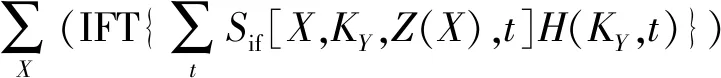
(12)

本文成像算法具体流程如下：

(1)划分成像区域。将目标二维成像平面划分为P行Q列的区域，具体划分大小由系统能提供的最小和实际所需目标分辨率决定。

(2)中频信号预处理。假设俯仰方向等效后的阵元个数为N，水平方向采样数为M，时间维采样点数为Ns，则可以获得中频信号为M×N×Ns的三维矩阵，对矩阵沿俯仰方向作P点快速傅里叶变换(fast Fourier transform，FFT)，得到Sif(X,KY,t)。

(3)计算目标区域某一列q∈{1,2，…,Q}到某一水平采样处m∈{1,2，…,M}的径直距离R[xq_Xm]。

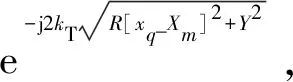
(5)选择将Sif(Xm,KY,t)与对应匹配滤波频域矩阵点乘，然后沿时间维相干累加，再沿俯仰方向做快速逆傅里叶变换(inverse fast fourier transform，IFFT)得到σ(xq_m,y,z0)。

(6)重复步骤(4)(5)将得到的结果沿X轴相干累加获得σ(xq,y,z0)。

(7)重复步骤(3)～(6)遍历Q获得最终图像σ(x,y,z0)，整体算法的流程如图7所示。

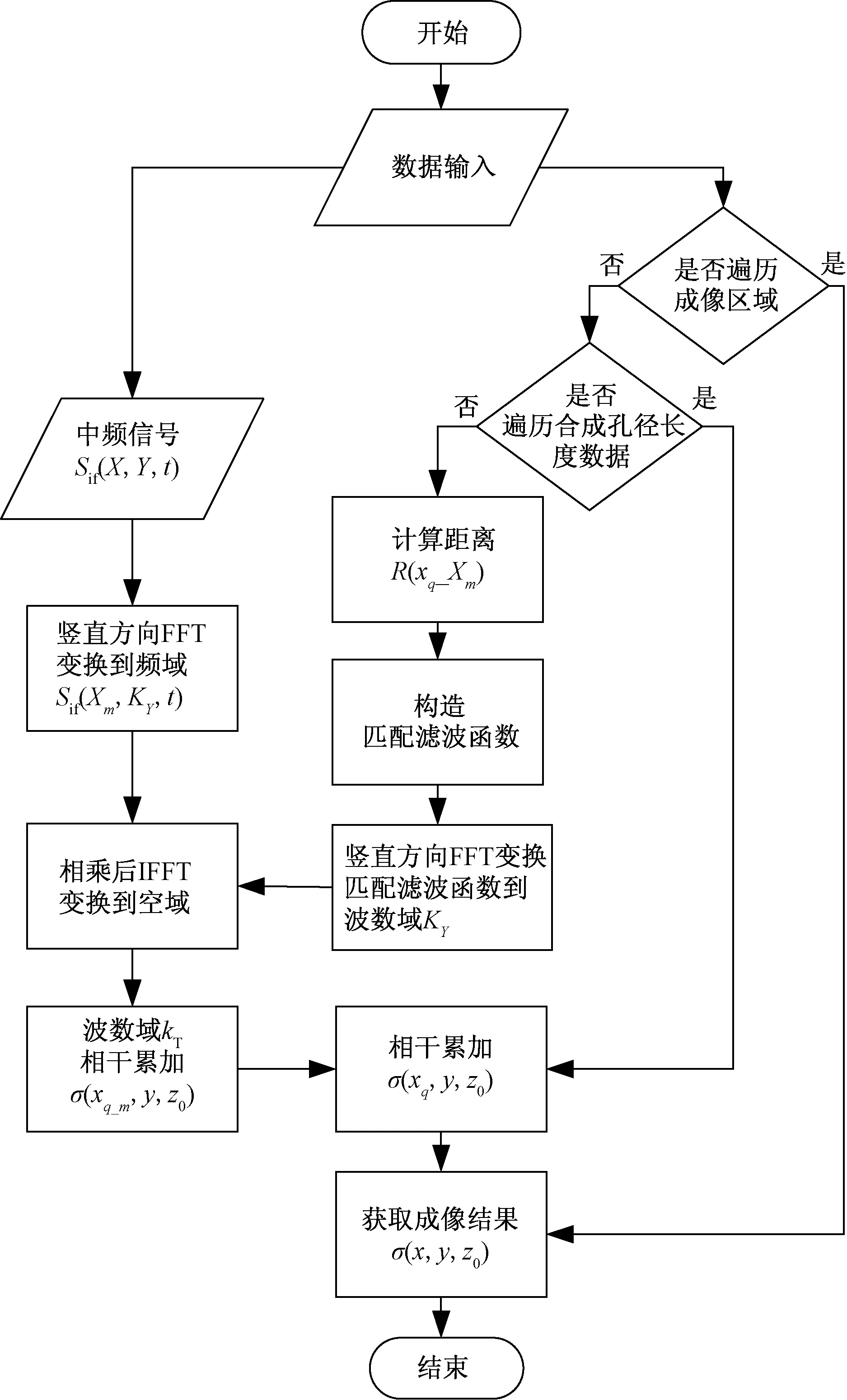
图7 快速成像算法流程Fig.7 The proposed fast imaging algorithm flow chart

算法时间复杂度分析：非直线轨迹场景下二维车载SAR成像方案对应BP成像算法时间复杂度为O[PQ(2MNNs+1)]。本文所提快速算法时间复杂度为O{Q[M(NsP+NsPlog2P+NsPlog2P+NsP+1+Plog2P)+1]}，其中第一项NsP和NsPlog2P表示得到匹配滤波二维矩阵以及进行FFT的运算量，第二项NsP和NsPlog2P表示对原始回波信号进行FFT并与匹配滤波频域矩阵相乘的运算量，由于目标在俯仰方向上的散射点数P通常大于俯仰方向阵元个数N，故以较大值为快速傅里叶变换运算点数，+1表示沿距离采样方向相干累积，Plog2P表示沿俯仰方向的IFFT运算。对于固定的俯仰方向通道数和水平采样点数，M、N为定值，Ns与发射信号及采样率有关亦为常数。根据上述分析，对同一目标拥有相同重构点数P、Q的情况下忽略低阶运算量，本文算法与BP算法复杂度的比值近似为N/log2P。

4.2 点目标仿真实验与分析

为了验证快速成像算法的有效性，首先分析算法在该场景下的点扩散函数。使用MATLAB软件仿真非直线运动轨迹下，位于坐标原点的单点目标回波数据，设置波形参数与阵元空间位置如表1所示，其中Z轴坐标根据预设数组添加到仿真。

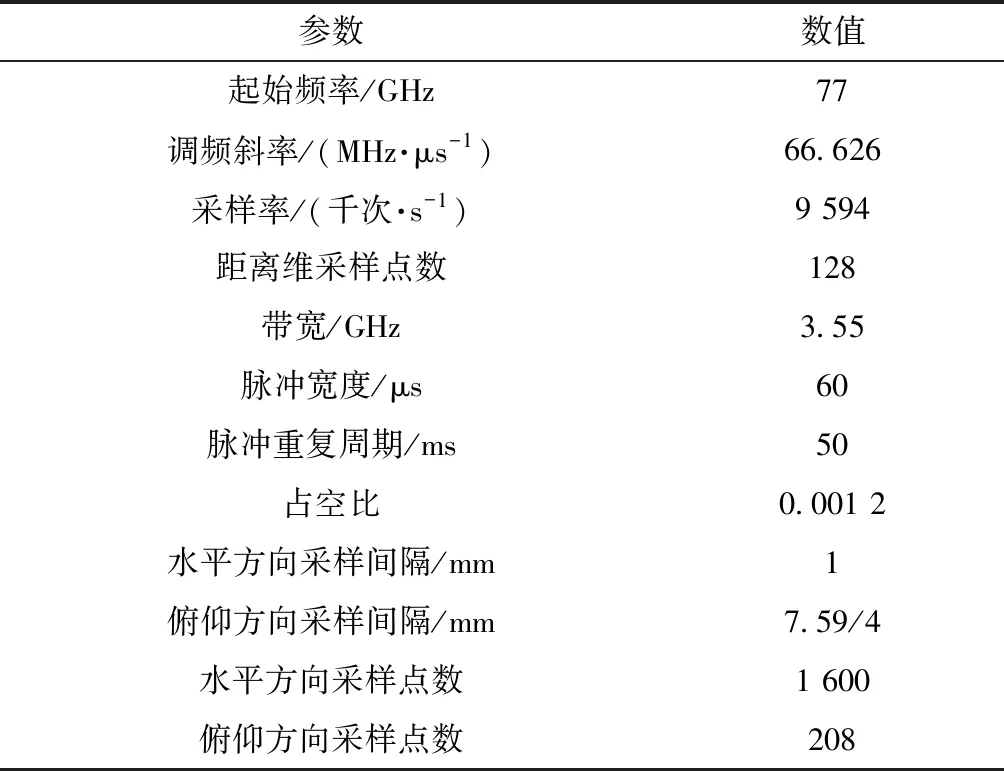
表1 仿真参数设置

使用BP算法和本文所提算法进行成像，归一化后取dB结果如图8所示，从图8中可以看出，两种成像算法的点目标均在正确的位置上实现了聚焦，并且具有较低的副瓣。将二维点扩散函数分别沿水平、俯仰方向进行截断，得到结果如图9所示。由于水平方向积累的合成孔径长度大于俯仰方向等效阵列孔径长度，所以图9(b)中显示出更窄的主瓣。而车辆在水平方向的非直线运动，导致该方向的点扩散函数呈现不规则副瓣曲线。

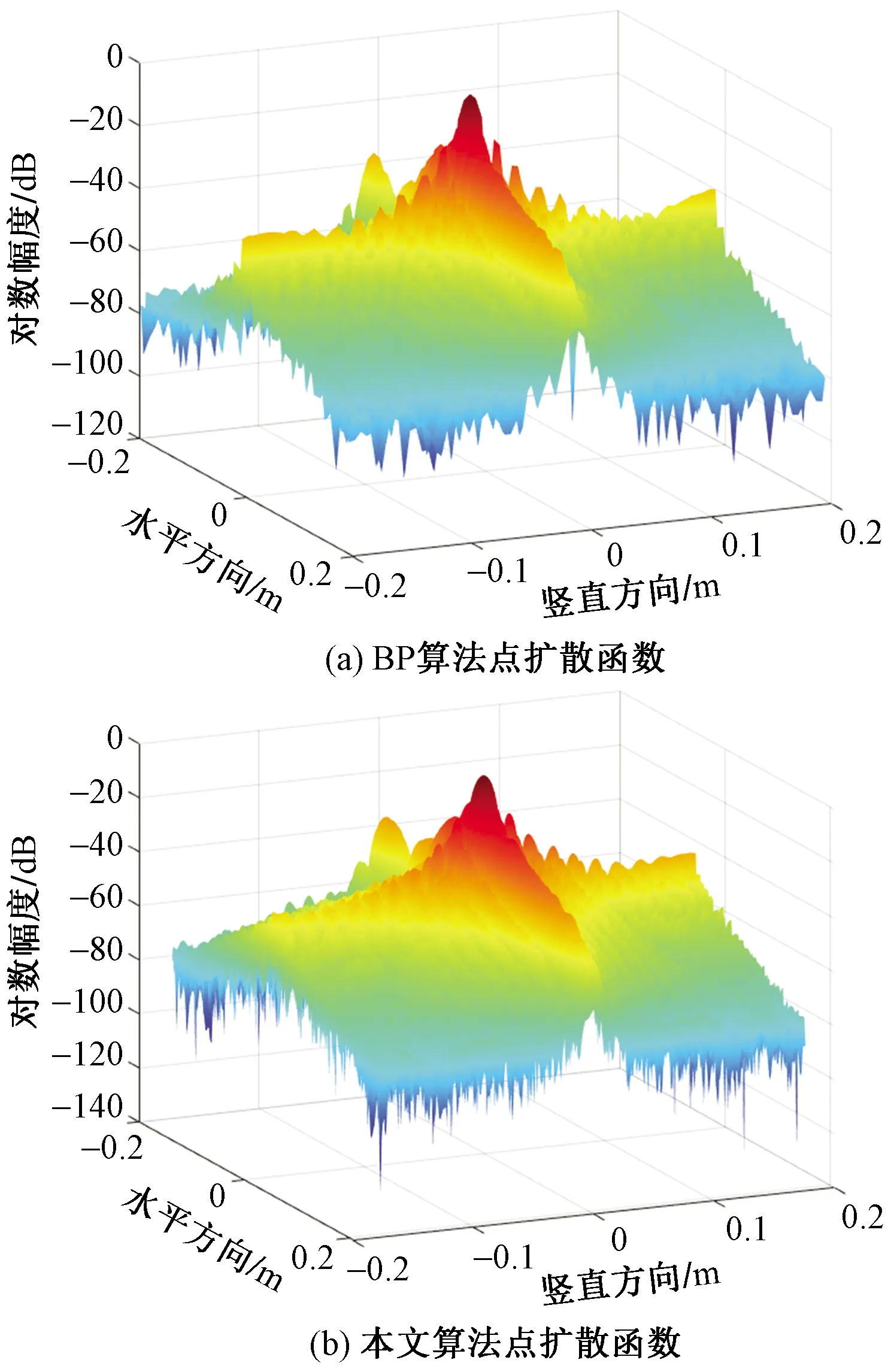
图8 点扩散函数成像结果Fig.8 Point spread function imaging results

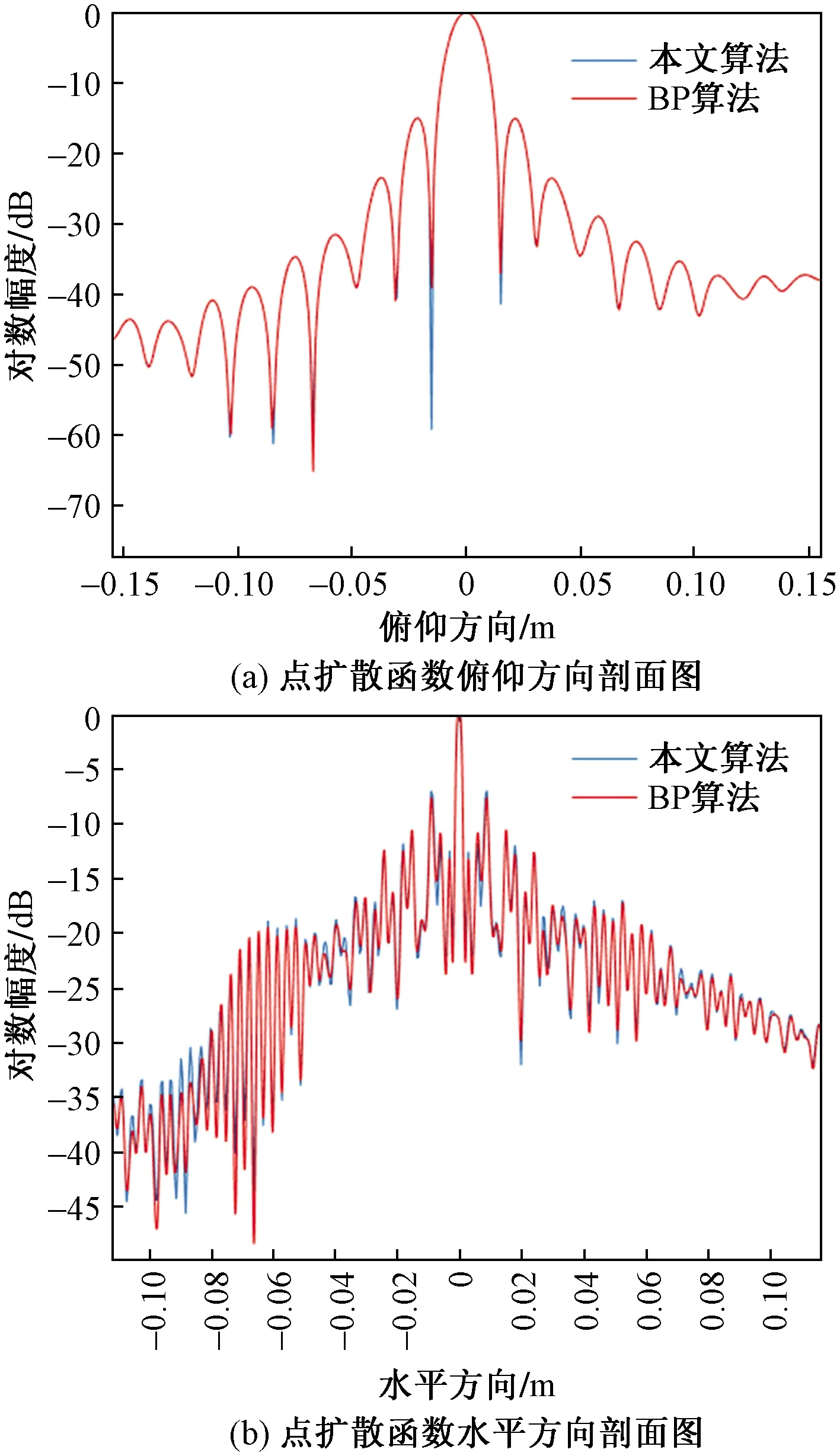
图9 点扩散函数剖面图Fig.9 Point spread function profile

为了具体比较两算法对点目标的成像效果，对不同方向的评价指标进行数值分析。计算点扩散函数参数指标主瓣3 dB带宽(impulse response width，IRW)和峰值旁瓣比(peak-side-lobe ratio，PSLR)的结果如表2，可以看出本文算法和BP算法重构结果的参数数值接近，表明对于中心点目标的成像效果基本一致，与上文理论推导相符。

表2 点扩散函数客观评价

4.3 二维目标仿真实验与分析

为了研究非直线轨迹下该快速成像算法对于二维目标的重构效果。仿真如图10所示，高度1 m，宽度1.2 m的目标，设置波形参数与表1相同。当车辆沿非直线轨迹运动时，由于随距离变化采得的数据，在不同时刻与目标Z轴方向的距离不同，使用同一距离进行补偿会造成图像散焦，做相干累加后无法正确重构图像，如图11所示，可见适用于直线轨迹下的二维匹配滤波算法在此场景不再适用。

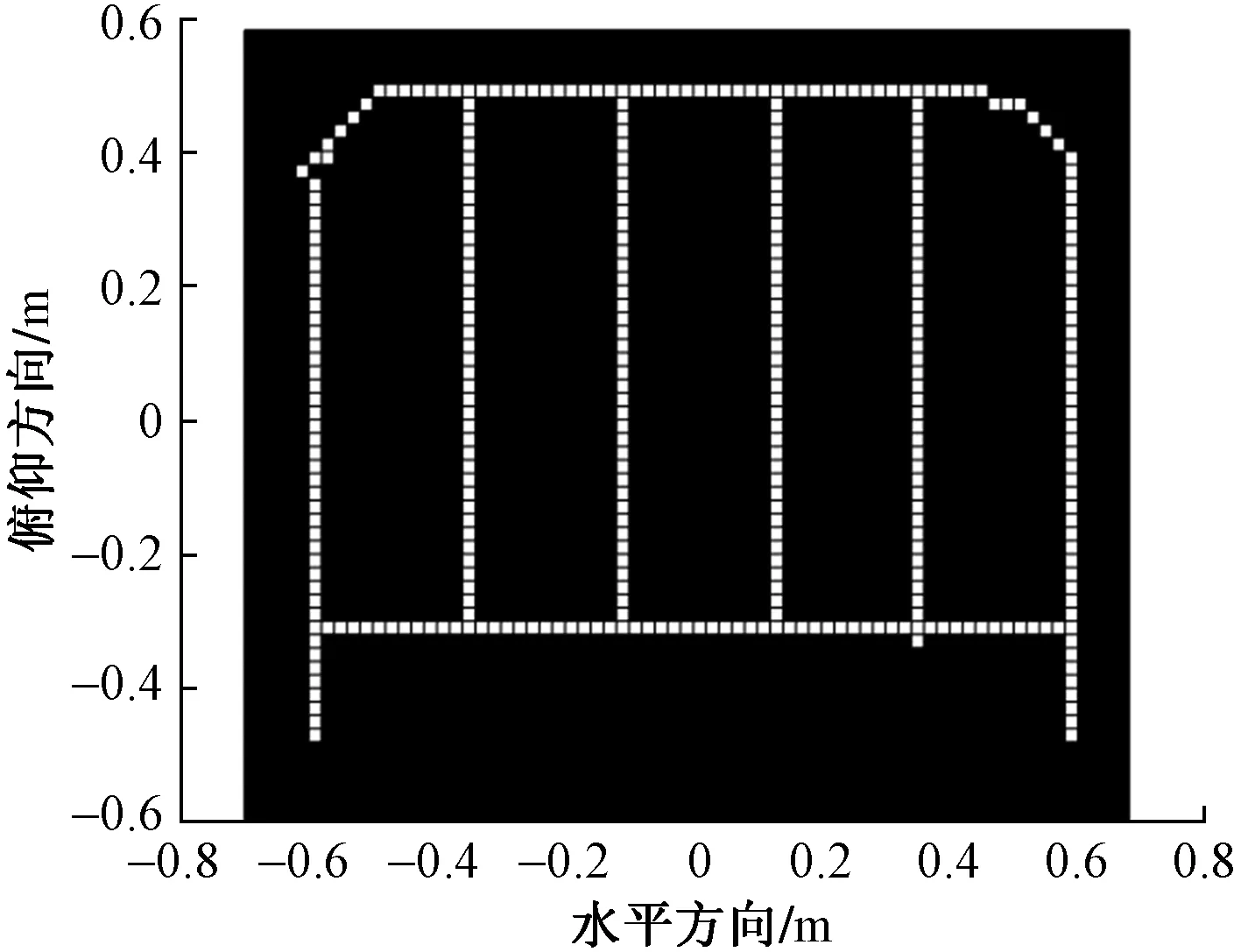
图10 反射系数图Fig.10 Reflection coefficient graph

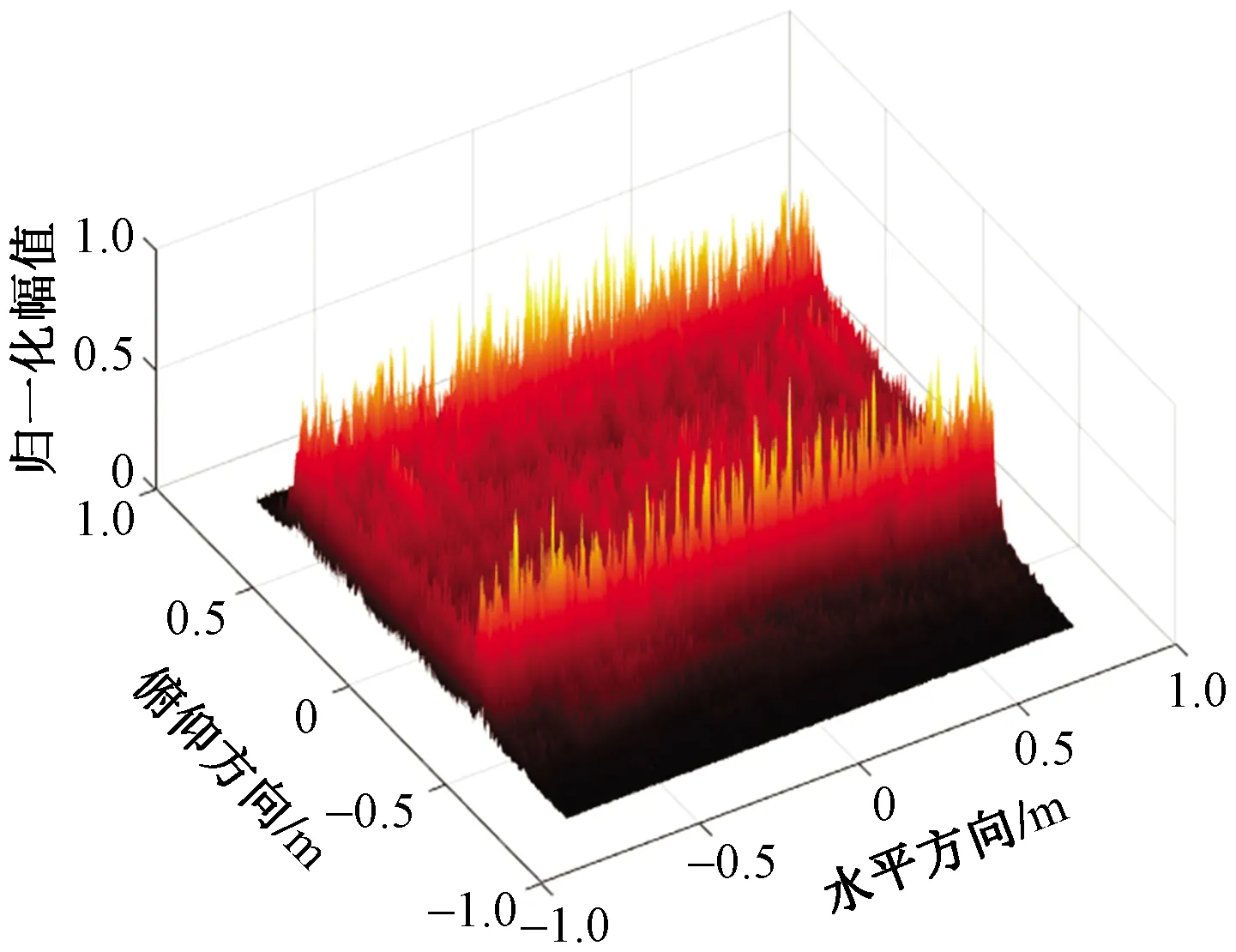
图11 二维匹配滤波成像结果Fig.11 Two-dimensional matched filter imaging result

使用BP算法成像结果如图12(a)所示。可以看出BP算法成像能够很好重构出目标二维像，但成像时间复杂度过高。另一方面本文算法利用该方案下的阵元特点，在Y轴方向采用波数域相乘代替空域卷积运算，成像结果如图12(b)所示。

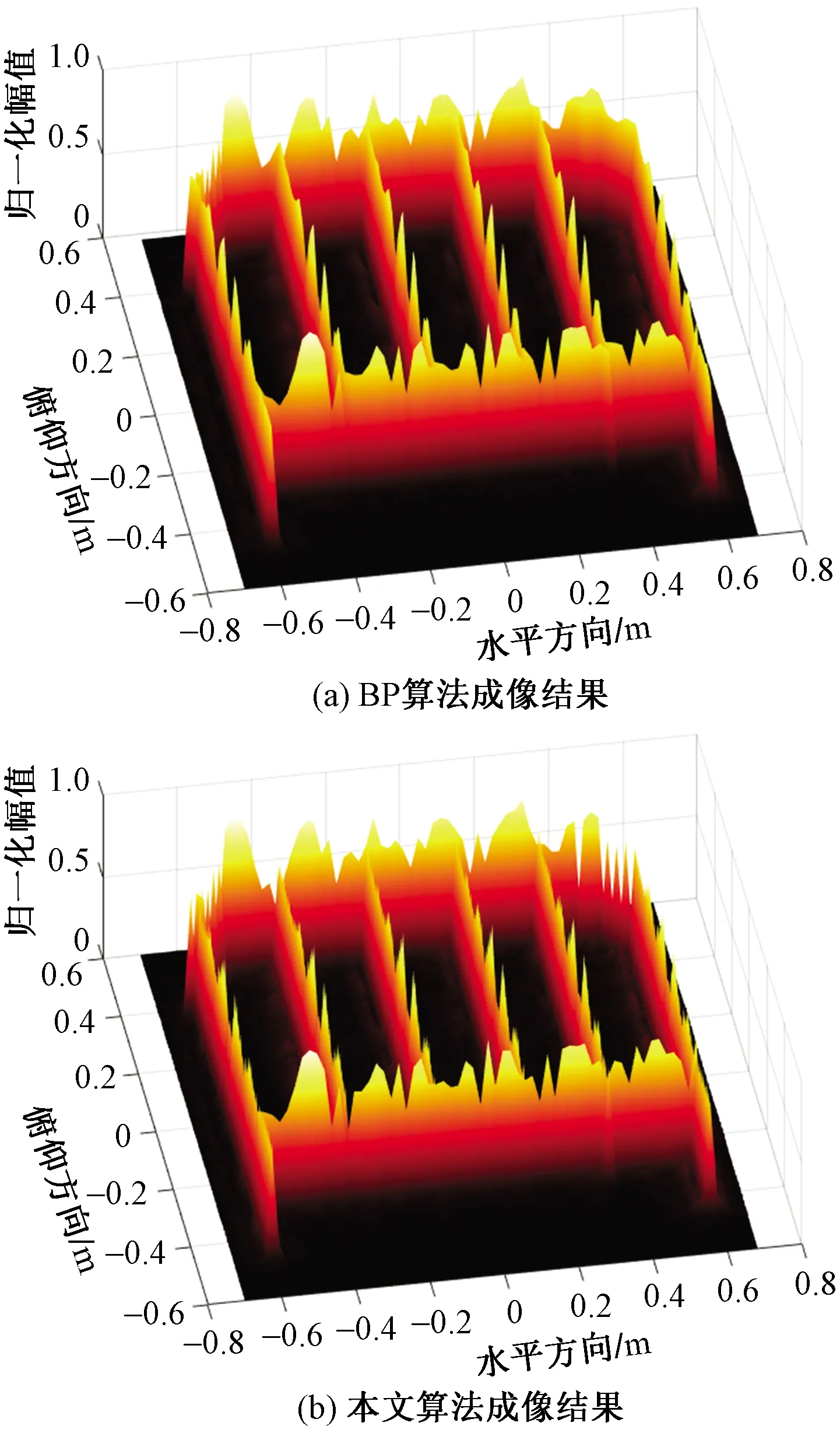
图12 非直线轨迹仿真成像结果Fig.12 Nonlinear trajectory imaging results

表3所示为仿真各成像算法所需时间对比，实验环境为MATLABR2018a，计算机硬件与系统环境为Intel(R) Xeon(R) Silver 4114 CPU @ 2.20 GHz Linux x86_64 +64 GB从表中可以看出对于相同尺寸的图像重构，本文所耗时间相较于BP算法降低了约20倍，与前面算法时间复杂度分析一致。

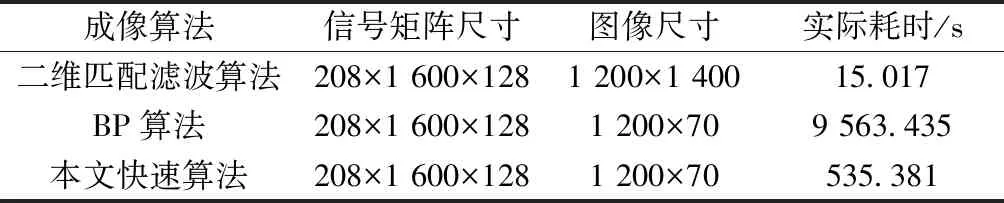
表3 成像算法耗时

为了进一步评价目标成像结果，采用图像熵(image entropy，IE)和图像均方根误差(root mean square error，RMSE)[17-18]进行数值分析。根据图像熵指标定义，图像灰度对比差异越明显，相应图像熵值越小，成像结果越清晰；相反当图像灰度分布越均匀，则重构图像越模糊，数值也较大。均方根误差指标则表明重构图像与所设反射系数误差的离散程度，其值越小说明与原反射系数差异越小，重构效果越好；反之则重构效果较差。计算得重构图像参数如表4所示，可以看出本文算法与BP算法所得成像结果图像熵数值相近，具有很好的图像聚焦程度，而二维匹配滤波方法重构的图像熵数值偏大，其图像也模糊不清。将重构图像降采样，计算归一化幅值与所设的反射系数图的RMSE指标，从数值计算结果看BP算法及本文算法重构结果误差均控制在约十分之一左右，具有良好的重构效果。

表4 成像结果客观评价

5 结论

讨论了毫米波雷达在车载SAR成像中的应用，首次提出一种二维车载SAR成像方案；接着提出一种采用线性导轨和商用MIMO雷达搭建数据采集系统的方法；最后对非直线轨迹快速成像算法进行研究，得到以下结论。

(1)使用线性导轨和商用MIMO雷达搭建的数据采集系统能够有效模拟车辆直线运动下的成像场景。

(2)所提二维车载SAR成像方案能够弥补现有一维SAR方案的不足，实现目标俯仰方向的分辨。说明该方案具有研究意义和应用前景

(3)非直线轨迹车载二维SAR成像场景下，本文所提快速算法相较于BP算法能够有效降低时间复杂度约N/log2P倍，并且具有良好图像重构效果。

本文所讨论方案可用于邻道停放车辆、护栏、路障及其他静止目标的感知等。另外宽带信号具备距离维的分辨能力，这使得在大带宽下该方案实际具有三维成像的潜力，将会在后续工作中做进一步研究。