渗透数学思想方法 促进学生思维提升
江苏省南通市海门区证大小学 柏沈燕
《义务教育数学课程标准(2011年版)》中把“数学基本思想”作为“四基”之一,充分说明了数学思想的重要性。学生在数学学习中,获得了数学思想,就等于获得了解决问题的经验和智慧,在面对新的问题时,就有了化“山穷水尽”为“柳暗花明”的数学思维能力。
一、渗透数形结合的思想策略
著名数学家华罗庚先生说过:“数无形时少直觉,形少数时难入微。”数形结合的思想,是根据数与形自身不同的特征,利用它们的对应关系,将抽象的数学语言与直观的图形结合起来解决问题的思想方法。
(一)以形助数,更直观
1.以形助数,厘清概念本质
数的产生源于生产生活实际的需要。利用生动、直观的图形,能将抽象的数学概念形象化、趣味化,让学生从中获得愉悦的情感体验,进而获取借助图形来理解数的概念的数学思想方法。
例如,教学“认识小数”一课,利用生活中熟悉的“0.4元”这个数展开教学,学生会读、会写,但是0.4元究竟比1元大还是小呢?教师利用多媒体投影出示一个长方形(图1)表示1元:
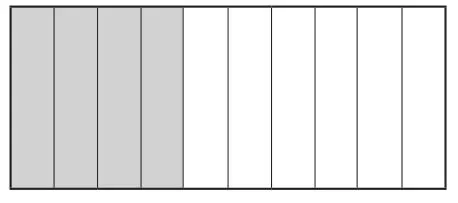
图1
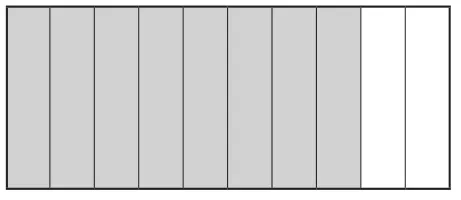
图2
通过演示,把一个长方形看作1元,平均分成10份,每一份就是0.1元,涂色部分就表示0.4元。通过观察,很明显0.4元小于1元。通过图1,还可以建立0.4与分数的联系,板书
接着,让学生通过长方形(图2)表示0.8元,再想一想0.8与哪一个分数相等。学生通过直观的图形认识了抽象的小数,不仅有效沟通了小数与整数、小数与分数之间的联系,而且对用图形沟通新旧知识之间联系的数学思想方法有了较为感性的体验。
2.以形助数,内化计算法则
计算教学一直以来都是比较枯燥而又抽象的。利用图形可以将抽象的数学知识、复杂的运算从表象上变得形象、直观,使学生对计算法则有了较为愉悦和深刻的体验,从而不仅内化了计算法则,也感悟到可以借助图形来突破学习难点的数学思想方法。
例如,教学“分数除法”一课,教师出示例题:在一个量杯里有升牛奶,把它平均分给2个小朋友喝,每个小朋友可以喝到多少升?
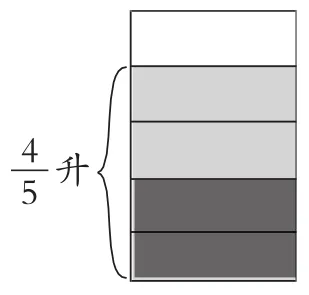
图3

(二)以数解形,助思维
“形”的优势是直观、形象,随着学生数学学习的深入,需要借助简洁清晰的数学描述、结构化的模型表达“形”的特征,才能更好地诠释数学抽象化和形象化互相结合、相辅相成的魅力,不仅能准确把握“形”的特点,更能掌握数学思想方法。
1.以数解形,揭示图形特点
进入中高年级,数学教材中出现了计算平面图形周长和面积、立体图形的表面积和体积的内容。这些几何问题的出现,不仅需要学生有较强的空间观念,有时也需要通过计算才能获得正确的结论。例如,“用24根1厘米长的小棒围长方形或者正方形,你能有多少种不同的围法?怎么围面积最大?你有什么发现?”这是一道关于“形”的问题,但是通过直观判断很难得出准确的答案,只有通过用数字一一列举出所有情况,才能准确知道一共有多少种围法,什么情况下面积最大。
经过具体数字的一一列举,完成下表可以得到:一共有6种围法,当长和宽都等于6,也就是长和宽的长度最接近时,面积最大。通过“数”字的列举、计算、研究,使得学生对图形周长和面积之间的关系有了更加深刻的理性认识。
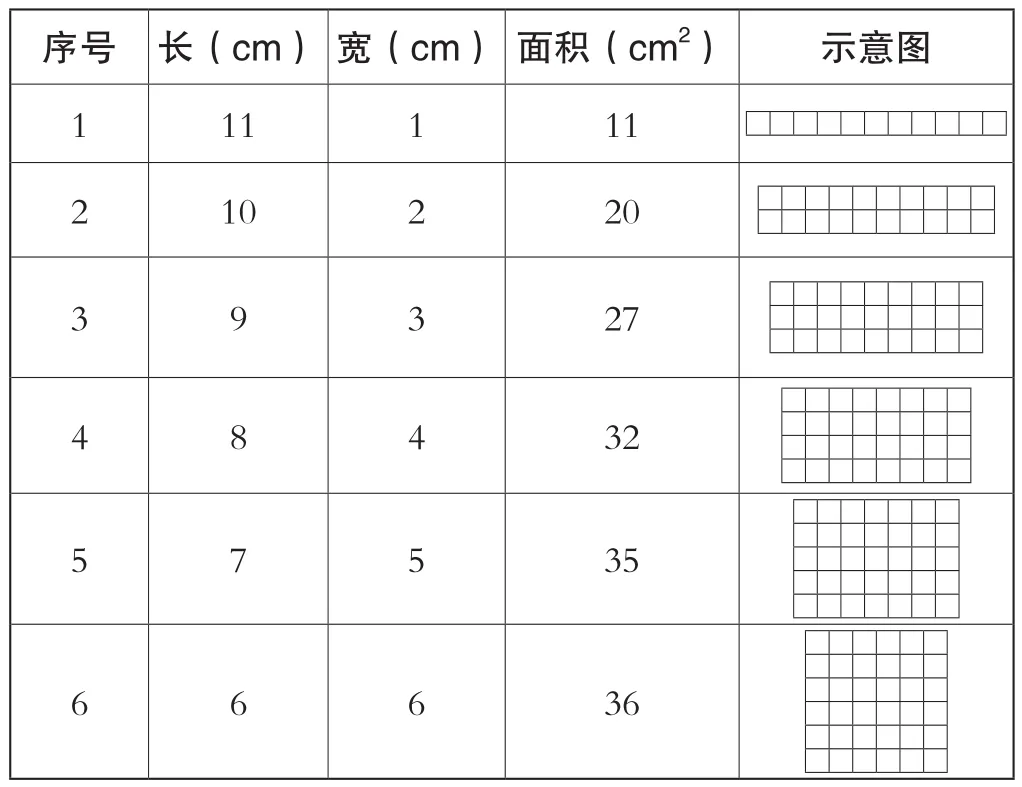
序号 长(cm) 宽(cm) 面积(cm2) 示意图1 11 1 11 2 10 2 20 3 9 3 27 4 8 4 32 5 7 5 35 6 6 6 36
2.以数解形,渗透代数思想
例如,苏教版五年级上册“平行四边形”一课,学生通过操作演绎推导出平行四边形公式后,教师在练习中安排了画平行四边形的练习(如图4)。
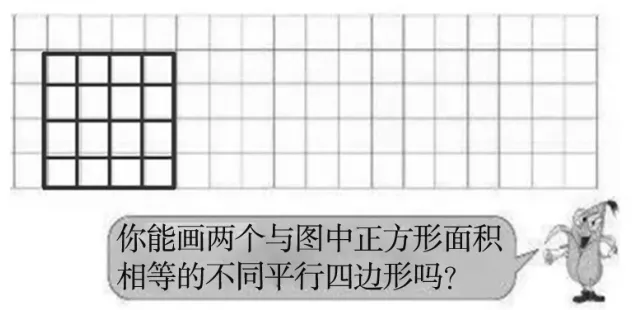
图4
学生在解题时,需要运用平行四边形的公式S=a×h进行代数思维。由图4可知正方形的边长是4cm,面积是16平方厘米。在练习中,较多的同学利用直观定式思维,画出了底是4cm、高是4cm的平行四边形。交流中,教师顺势点拨,要求与长方形面积相等,即面积只要等于16平方厘米的平行四边形就符合要求了,那么乘积是16的还有哪些底和高呢?一句话激起千层浪,学生利用代数思维,想到了还有16×1=16,8×2=16。通过展示交流,发现即使底和高相等,画出的平行四边形形状也是千姿百态的。
数形结合的思想在数学学习中无处不在、无时不在,将数和形有机结合帮助学生在形象思维和抽象思维之间搭起一座桥梁,让数学学习变得简单有趣。
二、渗透转化的思想策略
转化的思想策略,它在小学各年级的教材中都有体现。随着年级升高、数学知识不断增长,转化的数学思想也悄悄化为学生的一种数学学习能力,潜移默化地促进学生数学认知的发展。运用转化的思想策略,可以将新知转化为旧知,可以将复杂的问题转化为简单的问题,还可以将抽象的问题转化为直观的问题。
(一)将新知转化为旧知
在小学数学教材中,很多的知识点蕴含着转化的数学思想方法,而学习的过程就是不断将新的知识通过某种途径转化为以前熟悉的知识。如学习小数乘法,先将小数乘法转化为整数乘法计算;如学习三角形内角和,通过操作把三角形的三个内角转化成一个平角;如学习圆柱体体积,将圆柱体通过切割转化成长方体,从而推导出圆柱体体积公式。在教学这些内容的过程中,教师一定要把握好新旧知识之间的生长点,不仅要让学生掌握知识,知道知识的由来,更要让学生体会其中的数学思想方法。
(二)将复杂的问题转化成简单的问题
苏教版六年级上册“简单的分数乘法实际问题”一课,学生已经掌握了“求一个数是另一个数的几分之几是多少,用乘法计算”的分数乘法实际问题。教师出示问题:六年级同学为元旦晚会准备了鲜花,各种花的朵数如图5所示,其中黄花有50朵,红花比黄花多多少朵?
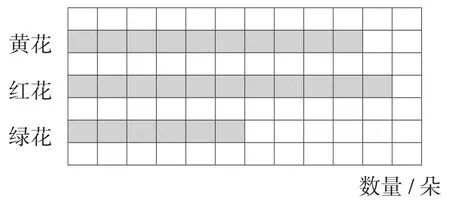
图5
看似简单的问题,对于学生来讲却是思维的一次跳跃,所以教师要善于为学生提供一把梯子,把复杂的问题转化为简单的问题。结合自主学习单的要求,先理解“红花比黄花多的含义,抓住关键句子把问题说透,即“红花比黄花多的朵数就是黄花的在解决问题的最后,教师要通过对解题过程的回顾,让学生深刻感受到运用转化方法可以将复杂的问题变得简单,即深刻理解转化对解题无穷的价值,让学生对数学从畏惧心理到产生更多的探索欲。
(三)将抽象的问题转化为直观的问题
解决倍数关系的问题,是学生“解决问题”中较难的一部分。解答此类问题时需要分析、比较,还要准确找到“单位1”,即一份的量是谁。例如,小明和小芳共有邮票120枚,如果小明送给小芳18枚,小明邮票的张数就正好是小芳的3倍,问原来小明和小芳的邮票张数。
面对抽象的文字和复杂的条件,学生感到解题很困难。这时如果把抽象的题意用画图的方式直观地表示出来,问题就迎刃而解了。(如图6)
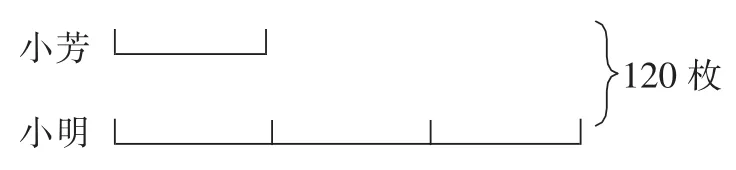
图6
除了用线段图表示,教师可以鼓励学生用不同的方法直观表示出小明和小芳之间的3倍关系,只要能厘清小芳是1份,小明有这样的3份,就能求出现在小明和小芳各有邮票多少张,进而求出他们原来的邮票张数。这种利用画图的策略将抽象的问题转化为直观的问题,是数学学习中最常用的方法之一,也是数学思想方法的一把金钥匙。
对于学生的数学学习,最终留给学生的不是加减乘除,而是数学思想方法。只有有了数学思想方法,学生才具备了可持续发展的数学能力。数学思想方法应该润物无声地在恰当的情境中滋养给学生,应该是坚持不懈地蕴含在数学的教与学中,逐步地由体验到明确,最终成为学生强大的思维动力。

