在经历中发现 在探究中建模——“分率变化引起面积变化”教学实录与评析

江苏省常州市怀德苑小学 徐丽华

【内容简述】苏教版六年级上册第五单元“分数四则混合运算”后安排了“动手做”，这一内容是这样描述的：

【教学目标】

1.帮助学生借助数学实验探索分率变化引起面积的变化规律问题的模型。

2.让学生经历“提出猜想—探究验证—总结应用”的探究过程，进一步发展学生推理的能力，提升学生数学思维力，激发学生学习数学的兴趣。

【教学重难点】探究解决此类面积变化的模型规律。

【学情分析】

六年级学生具有较强的计算能力和较丰富的解决问题能力，会根据题意选择适当的方法和策略解决实际问题。因而本课教学的重难点在于帮助学生调动已有知识经验，让学生在画图、操作、计算中观察、比较、总结，在一次次经历中研究出分率变化引起面积变化的规律，促使学生主动探究，建构知识模型，提升思维品质。

【教学准备】磁力片、方格纸、学习实验单。

【教学设计】如下。

一、情境中激趣，初建模型

师：我们学校自从开辟了“魔法农学院”，每个班都在自己的自留田上种植蔬菜，为了奖励我们班种植效果不错，学校想把咱班菜圃扩大些，你有什么办法吗？

生：把长增大，或者把宽增大。

生：可以把长和宽同时增大。

师：是呀！如果把长、宽增大，菜圃的面积也就随之变大了。今天这节课我们就来研究面积的变化规律。

评析：课始，结合学校开展的品格提升劳动教育，创设魔法农学院种植需要扩大面积的情境，引发学生探究面积变化规律的热情和欲望，让学生感知要扩大长方形面积需要增大长或宽，初步建构“形”与“量”的变化结合，为后面进一步探讨整体建构铺下伏笔。

二、多维中探究，经历模型

（一）第一次实验：从特例出发建构模型

师：猜想对吗？怎样得到正确的结论？

生：可以动手画一画，算一算；可以拼一拼，比一比。

师：那就采用你们自己的方法动手实验一下吧！

出示实验要求：

1.用自己喜欢的方法：可以拼一拼、画一画、比一比等，表示出变化后的长方形。

2.写一写或算一算：变化后长方形的面积是原来的几分之几？

生1：用磁力片拼一拼。

假设长是4厘米，宽是2厘米，就用8块磁力片拼成一个长方形，根据题意，长和宽分别增加那么现在长方形用磁力片拼成的新长方形就需要用到18块，新长方形的面积与原面积的比是18:8，化简成分数后就是

师：通过磁力片的拼摆，让我们从比与分率的角度思考，能在直观的操作中体会到新面积与原面积之间的关系。

生2：用方格纸画一画。

借用方格纸图更容易看出新长方形和原长方形之间的面积关系。从图中直接能得出新长方形的面积是原长方形面积的

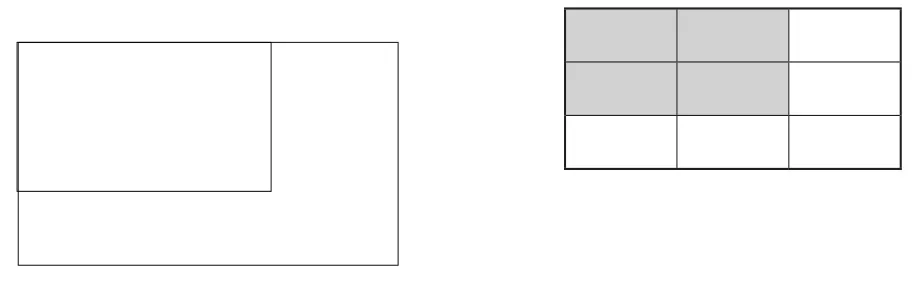
师：不管是刚才的磁力片，还是现在的画图，大家采用的实验工具不同，但通过数形结合的方式都能获得同一种结论。

生3：用计算的方法。

原长方形长4厘米，宽2厘米，新长方形的长是6厘米，宽是3厘米，面积是6×3=18（平方厘米），而原长方形的面积是8平方厘米，新长方形的面积就是原来面积的

师：计算出数据，可以精确地算出结果，得到结论。

评析：探究分率的变化引起长方形面积变化规律，需要从具体的图形、数据入手逐步建构。为此，教师创设开放的问题情境，让学生先进行猜测，然后从“拼一拼”“比一比”“画一画”“算一算”等环节逐步验证，学生从简单的特例开始研究，把抽象的比较在直观具体的素材和学生亲身经历丰富多彩的学习操作活动中，发现新长方形和原来长方形面积间的关系，进而为研究两者面积关系建构模型，为特例到众例的探究做好充分的准备。

（二）第二次实验：从众例出发建构模型

师：刚才我们通过拼一拼、画一画、算一算，发现将这个长4厘米，宽2厘米的长方形的长和宽分别增加得出变化后的面积是原来的研究到这，你们有什么疑问吗？

生：仅从一个长4厘米，宽2厘米的长方形，得出变化后的面积是原来的那么其他的长方形会不会还是原来的

师：是呀！每位同学想的长方形可能都不一样，将它的长和宽分别增加变化后的面积又会是原来的几分之几呢？这就需要每位同学再次去求证。

出示实验要求：

（1）举例验证：用你自己喜欢的方法去比较。

（2）交流分享：小组汇总所有情况，说一说形状不同的长方形，你又有什么发现？

生1：我的长方形长是10厘米，宽是6厘米，经过计算比较发现变化后长方形的面积是原来的

生2：我的长方形长是12厘米，宽是8厘米，也能得出变化后长方形的面积是原来的

师：虽然同学们心中的长、宽都不一样，但是都能得出一致的结论。仔细观察一下，得出的结论与什么相关？与什么无关呢？

生：与长和宽的数据没有关系，但与长和宽增加的分数有关。

评析：学生在第一次特例实验操作中已经初步建构面积变化间的关系，但是数学学习的过程，往往都是从特殊开始，通过不断验证、总结、归纳，得出规律。教学中应注重让学生经历从特殊到一般的数学思想。

（三）第三次实验：从多维度出发建构模型

师：长和宽的数据不断在变化，我们为了方便研究，有什么方法可以表示出所有情况？

生：可以用字母来表示。

师：那原来的面积就是ab，根据题意，你能用含有字母的式子表示现在的长、宽和面积吗？自己动手试一试。

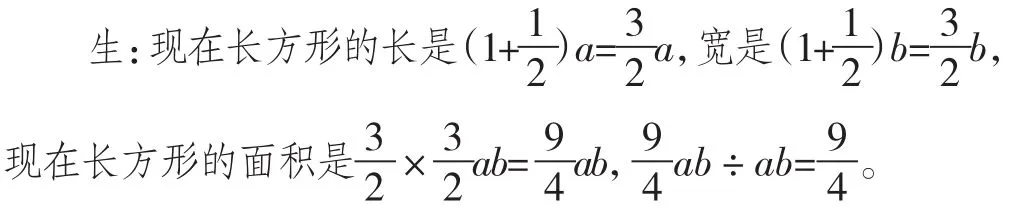
师： 我们通过演绎推理，用字母表示所有的例子，现在我们可以得出变化后长方形的面积是原来的如果用积的变化规律能否解释？谁能试着说一说？

师：那长方形面积的变化与什么有关？

生：与分率有关。

评析：学生在举例过程中发现无法把所有情况一一列举，当出现矛盾冲突后想到用数学符号来抽象概括。但是符号化思想的形成需要一个循序渐进的过程，因此，用字母表示所有情况不能作为一个单纯的知识点学习，需要让学生在一个又一个问题情境中关注学习方法，关注能力技巧训练，把握其中渗透的数学符号化思想，为算术思维向代数思维的过渡打下坚实的基础。

三、深度中思考，完善模型

（一）第四次实验：从深层次出发建构模型

四、变式中应用，拓宽模型

师：由于菜圃面积的扩大，影响到了旁边花圃的面

评析：通过变式梯度练习，让学生在面对复杂问题时，能够根据问题引导对知识进行系统梳理，利用建构的已有知识模型顺势迁移，将数形巧妙结合，从而找到最优方法解决问题，突出思维思考，使数学深度学习真实地发生，让学习更深入、更有效。

五、回顾中反思，积累模型

师：这节课我们一起探究了分率变化引起面积变化的规律，回顾一下，你是怎样得出规律的？还有什么新的疑惑或是想研究的问题？准备怎么去探究？

评析：在一次次回顾总结中帮助学生系统梳理知识，形成解决问题的策略模型，为今后研究新问题积累经验。