基于优化的GA-BP及其在葡萄酒质量预测的应用

赵 峰，姜胜兵

(安徽工业大学 管理科学与工程学院，安徽 马鞍山 243032)

目前，对于葡萄酒质量的评定，国际上并没有一个统一的标准，大多数企业对于葡萄酒的评定都是聘请一些有资质的品酒员来品评的.一般情况下，是通过品酒员在品尝葡萄酒后按照分类指标对其进行打分，再求出综合得分，因此所得到分数的高低是衡量葡萄酒的质量的重要标准.但是，在实际中，聘请有资质的品酒员来对葡萄酒进行品评不是一件容易的事情，而且人为的主观因素也会影响到评价的结果.葡萄酒品质的好坏是一个抽象的概念，但对它的理解可以直接与葡萄酒的化学成分有关[1]，所以葡萄酒质量的好坏很大的程度上是与葡萄酒的理化指标是密切相关的，若是能够找到他们之间合理的关系，那么即便没有品酒员，也可以完成对葡萄酒的评价.对于葡萄酒评价有很多的方法，常见的方法有多元回归、趋势预测等，但因为函数关系式的复杂，难以确定下来，导致建立的模型在预测的结果上不是很准确.

人工神经网络的非线性逼近能力很好，而且一个简单的三层BP神经网络能够满足一般的映射要求，预测精度较高，所以应用较为广泛[2-4].但BP算法也是有一定的缺陷的，网络的权值和阈值是随机产生的，并且学习率也是依据经验设定的，导致在有多个局部极小值时候，模型无法跳出极小值.

遗传算法是全局优化搜索的算法，对目标函数空间进行并行式搜索，选择适应度值大的个体.于是很多学者利用遗传算法和神经网络的特点取得了很多不错的成效[5-7]，比较广泛的是通过遗传算法寻找神经网络初始的权值和阈值[8-9].

针对葡萄酒的质量评价，Paulo Cortez、António Cerdeira[10]等人采用支持向量机、多元回归及神经网络方法基于葡萄酒理化指标对葡萄酒偏好建模分析.夏铭泽、石春鹏[11]通过支持向量机对葡萄酒的理化指标进行建模分析来预测葡萄酒质量.姚燕云、蔡尚珍[12]采用基于LASSO回归对葡萄酒进行评价研究，降低了评价与测试的成本.毕艳亮、宁芊[13]等人在遗传算法中引入免疫记忆机制保护优秀个体、对适应度排序靠后的个体以更高的概率进行变异和多点交叉的方式优化神经网络，提高了BP模型的准确率.孙文兵[14]因葡萄酒的理化指标过多，通过遗传算法筛选理化指标并优化神经网络的权值和阈值减少模型时间，提高模型的泛化能力.通常情况下，遗传算法在寻优时，交叉率一般是不变的.因此，基于适应度值改变交叉率，建立GA-BP模型对葡萄酒质量预测，因为染色体长度关系，可以采用多变异位方式来增强算法的搜索能力，使得优化后的模型有明显效果.

1 基本算法简介

1.1 BP神经网络

BP神经网络算法，于1986年由Rumelhant和Hinton等人首次提出，是人工神经网络中较为经典的学习算法.BP神经网络主要包含一个输入层、一个或者多个隐藏层、以及一个输出层，每一层都含有若干个神经元，输入值、权值、阈值和激活函数决定着每个神经元的输出值.BP神经网络的正向传播是输入信号先从输入层传入隐含层，再传向输出层，从而产生输出信号.误差反向传播是因为网络模型的实际输出值与期望输出值之间存在差值，即误差信号.在反向传播的过程中，误差信号是由输出层逐渐的向前一层传播，调节网络的权值和阈值，使得网络的实际输出更加接近期望输出.

BP神经网络的输出层和隐含层上的一个神经元j的输出公式如下：

(1)

其中：xi表示神经元j的各个输入值；而Oj表示神经元j输出值；wij表示对应的输入i与神经元j之间的各个连接权值；fj表示神经元j的激活函数；通常使用的激活函数Sigmoid函数：y=1/(1+e-x)；bj表示的是神经元j的阈值.

BP神经网络主要是通过网络的各层节点的个数，以及相邻层节点之间的连接权值来存储信息的.隐含层的节点个数、学习率是影响网络结构的主要参数.输入层与输出层的节点个数通常是由应用的问题来确定的，隐含层节点个数则是由用户凭借经验决定的，节点个数过少会影响网络的有效性，节点个数过多则会增加网络的训练时间.学习率通常选取0.01～0.99之间.

常用的隐含层选择个数经验公式如下：

(2)

其中：h表示隐含层节点个数；m表示输入层节点个数；n表示输出层节点个数；a为[0，10]之间的任意整数.

误差的损失函数如下：

(3)

其中：w，b分别表示权值和阈值；M表示样本数量；di表示第i个样本的期望输出；Oi表示第i个样本的网络实际输出；f(w,b)即为损失函数.

1.2 遗传算法

遗传算法于1970年由Holland教授通过模拟自然进化过程而提出来的一种算法.遗传算法是模拟自然生物的个体进化过程，自适应搜索优化问题的最优解，遗传算法还能够进行有效的局部搜索，找出潜在的优化解[15].

遗传算法是对需要优化的问题参数进行编码,其基本操作如下：

1)初始化种群.随机产生N个个体作为初始化种群，以保证种群有足够的多样性；

2)适应度函数.是区分种群中个体好坏的标准，适应度函数增大的方向是遗传算法变化的方向；

3)选择运算.运用轮盘赌选择法，按照染色体的累积概率选择染色体进入下一代；

4)交叉运算.随机选择两条染色体，再生成一个随机数，若小于交叉率则进行交叉，产生两个新的个体；

5)变异运算.随机选择一条染色体，再生成一个随机数，若小于变异率则进行变异，产生一个新的个体；

6)种群更新.将通过遗传操作获得好的解保存下来，最终得到一个最优的种群.

2 神经网络模型及优化

2.1 神经网络模型建立

2.1.1 构建BP神经网络模型

因为白葡萄酒有十一项指标，所以神经网络的输入端口的神经元为11个，输出端口的神经元为1个，隐含层神经元个数通过经验公式(2)最终确定为8个时对数据的测试效果最好.因此可以将神经网络的模型确定为11—8—1，并且隐含层和输出层的激活函数使用的都是Sigmoid函数.

BP神经网络中还存在着一些缺陷: 1)神经网络的学习率是不确定的，不容易选取适当的值；2)神经网络的初始权值和阈值都是随机生成的，容易使其陷入到局部最优，影响网络的训练效果.这里对其做了一些改进：1)学习率的设置不再是固定的，改用自适应学习率来提高网络的学习效率；2)遗传算法在寻优方面有很有效果，因此可以利用遗传算法寻找优秀的权值和阈值，以防止权值和阈值因为随机生成而使得神经网络的结果陷入到局部最优.

2.1.2 学习率的影响及改进

传统的神经网络在训练时所使用的是固定的学习率，对训练的结果产生很大的影响，但是学习率具体选择多少又是不确定的，学习率过小，训练次数越多，网络收敛的慢，学习率过大的，网络结构的稳定性差，因此考虑自适应学习率的方法.公式如下：

(4)

其中：λt为第t次训练时候的学习率；λt+1为第t+1次训练时候的学习率；ΔE为误差的变动量.

2.2 遗传算法优化BP神经网络模型

2.2.1 遗传算法的改进

1)初始种群与个体编码

随机产生N个个体作为初始种群，考虑到神经网络的输入节点个数为m、隐含层节点个数为h、输出层节点个数为n.在染色体进行编码是应该注意到以下问题：1)权值矩阵是一个二维矩阵，而染色体是一维的；2)权值和阈值是有多个的，但是一个染色体是只有一条的.因此将二维的权值矩阵映射成为一维的矩阵，并且将多个权值和阈值拼接成染色体.采用实数编码，每一个染色体其实是一个实数串，由网络模型的各层的连接权值、阈值组成，因此确定个体染色体的长度的公式如下：

L=m*h+h+h*n+n

(5)

2)适应度函数

适应度函数是区分种群中个体好坏的标准，对随机产生的权值和阈值，计算出产生的误差，适应度函数增大的方向就是遗传算法进化的方向.这里选择损失函数的倒数作为适应度函数：

(6)

其中：M表示训练集样本的数目，di表示的是第i个训练样本网络的期望输出，Oi表示第i个训练样本网络的实际输出.

3)选择运算

选择运算采用的是轮盘赌选择法，以此对染色体进行选择来产生个体数同样为N种群.在进行选择时，可能会有重复的个体，而重复的个体在进行交叉的时候是没有意义的，因此在选择的过程中还要将重复的个体剔除掉.

4)交叉运算

交叉运算采用的是单点交叉，从初始种群中选择两个配对的个体，随机设置一个交叉点，互换两个配对个体的部分染色体，然后形成两个新的个体.

交叉运算的目的是为了产生新的种群个体来提高种群的多样性，因此交叉率的取值对于遗传算法的性能有着十分重要的意义.一般标准的遗传算法采用的交叉率是固定的，就会导致算法早熟或者收敛速度慢等问题，但是合适的交叉率是并不容易发现的.若是交叉率过小，种群难以产生优秀的个体；若是交叉率过大，在算法后期，则使得种群中优良的个体难以保留.因此，本文采用的交叉率是随着适应度值的变化而变化，公式如下：

(7)

其中：Pc1=0.99，Pc2=0.4，fmax为群体中最大的适应度值；favg是每代群体的平均适应度值；f′是将要交叉的两个个体中较大的适应度值.

5)变异运算

由于染色体的长度较长，不适宜选择传统的单点变异操作，因此改变变异位数，采用自适应变异位数的方法，公式如下：

(8)

当变异算子以一定的概率对某个个体a的第k个基因发生变异时，采用的变异操作如下：

(9)

采用这种变异操作的优势在于：1)随机数r1的设置可以影响变异的程度；2)随机数r2的设置可以保证基因值以相等的概率增大或者减小，同时由于基因值上下界的存在保证了基因值的变化不会太大；3)采用自适应调整变异位数，并兼顾算法在全局和局部的均衡搜索能力，随着迭代次数的增加，变异的程度也在逐渐的减小，初期保证全局搜索能力较强，后期也保证了算法的局部搜索能力，能够促使个体也可以收敛到全局最优解.

2.2.2 遗传算法优化BP神经网络的权值和阈值

基于遗传算法优化的BP神经网络应用流程：

1)在创建BP神经网络，随机生成初始权值和阈值，对种群进行初始化，采用实数编码，确定种群数目；

2)计算适应度函数，按照轮盘赌选择法挑选最优的个体，然后将其插入到下一代种群中；

3)在新一代的种群中，通过交叉和变异产生新的个体；

4)将新的个体再插入到种群当中，并计算其适应度值；

5)若是可以找到满意的个体，则终止算法，否则转到第2)步；

6)在找到最优的个体之后，将该个体进行解码，得到优化后的权值和阈值，再将其用于BP神经网络当中.

具体GA-BP网络模型的流程图见图1.

图1 GA-BP网络模型流程图

3 模型应用

3.1 实验数据集

实验数据来源于UCI数据集中的winequality-white.csv文件，如表1所示，数据主要为一白葡萄酒的物理化学参数及专家为其质量的评分，由P·Cortez和A·Cerdeira等人提供，共有4 898条数据，主要参数有非挥发性酸、挥发性酸、柠檬酸、残糖、氯化物、游离二氧化硫、总二氧化硫、密度、酸碱度、硫酸盐和酒精含量共计十一项理化指标，而最终白葡萄酒的质量评测的结果是用0～10之间的分数表示.本文将数据拆分为两类，一类是作为训练集，包含4 700条数据，一类作为测试集，包含198条数据.由于白葡萄酒的各个指标的数量级不一致，会影响网络最终的映射结果，因此需要对全体数据进行归一化处理.归一化处理公式如下：

表1 葡萄酒样本各项理化数据

(10)

其中：tmin为每列数据的最小值，tmax为每列数据的最大值，t为需要归一化的数值.

3.2 实验结果与仿真分析

BP神经网络模型采用的是前文介绍的BP网络，初始学习率为λ=0.04，最大迭代次数iternum_max=800，最小可接受误差Eaverage_min=0.001.GA-BP模型的建立是采用前文中介绍的自适应遗传算法优化的BP神经网络模型，并对学习率进行优化，利用Anaconda软件实现的.在遗传算法中种群大小设置为100，最大迭代次数为500，交叉率采用自适应变化，变异率Pm=0.1，基因值的上界为15，基因值的下界为-15，设置的最大变异位数为10.

图2是遗传算法的适应度曲线，当种群进化到第300代之后得到了，适应度曲线开始稳定，寻找到最优的个体，种群的平均适应度值在稳定的过程中也存在着一些波动，这是由于遗传算法中存在着一些随机的因素造成的.

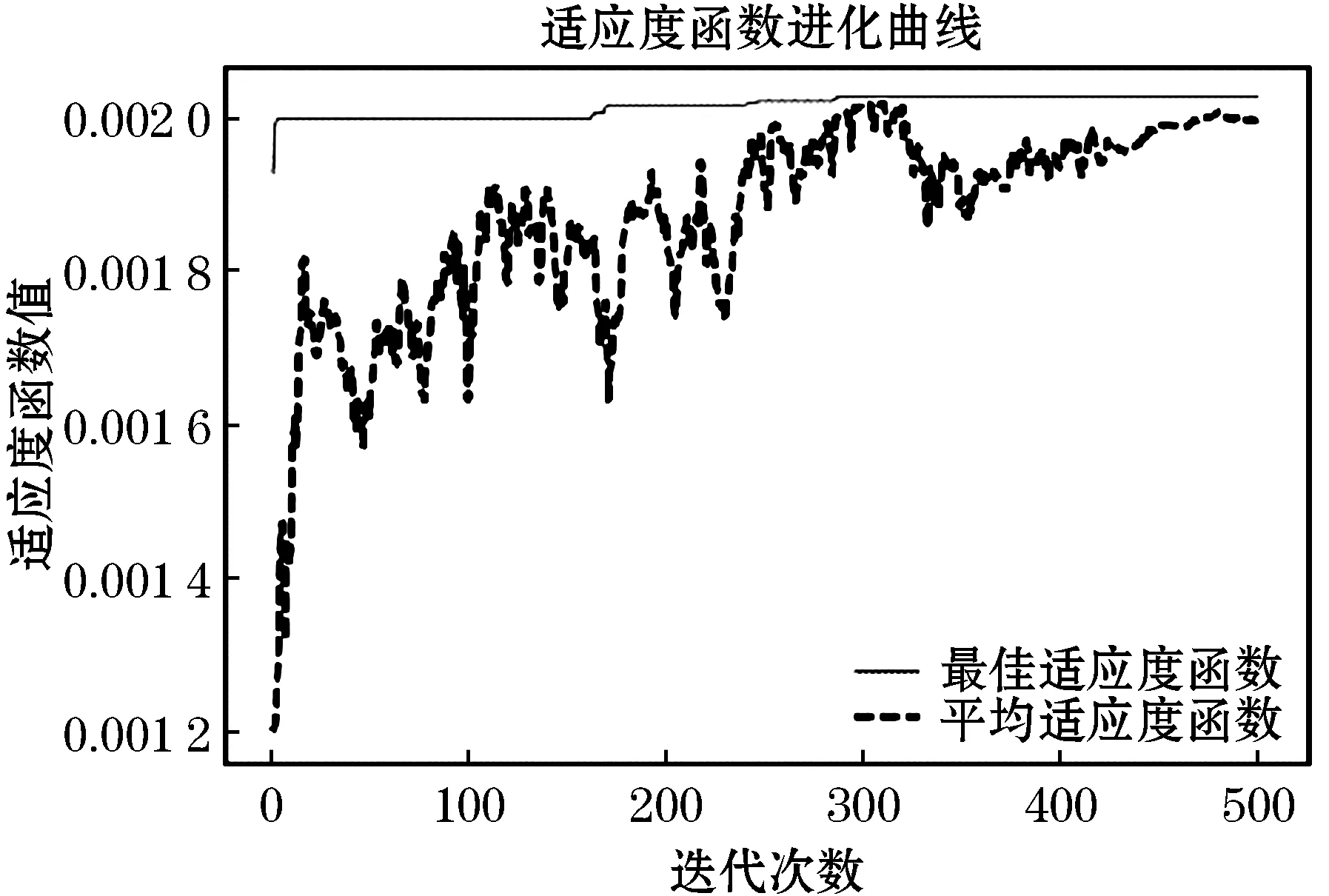
图2 种群适应度函数曲线

为了对实验结果有一个准确的判断，选择采用的评价指标是损失函数的平均误差，将每组数据通过损失函数求出损失值后求和再取其平均值.这里通过比较BP神经网络模型和GA-BP模型，得到BP神经网络与遗传算法优化的神经网络训练过程中归一化后的平均误差图，如图3所示，由此可知，经过遗传算法优化的神经网络在训练的初始误差比普通的神经网络的初始误差要低.普通的神经网络早早地就陷入了局部最小值而无法跳出，而经过优化的神经网络则不断地跳出局部最小值达到收敛.

由图3可知，在经过遗传算法优化BP神经网络之后，得到的优化后的权值和阈值，然后将得到的权值和阈值放入神经网络中，使得神经网络的收敛的结果更好.为了对比实验的科学性，表2的数据是分别对两个模型进行10次预测所产生的误差对比.

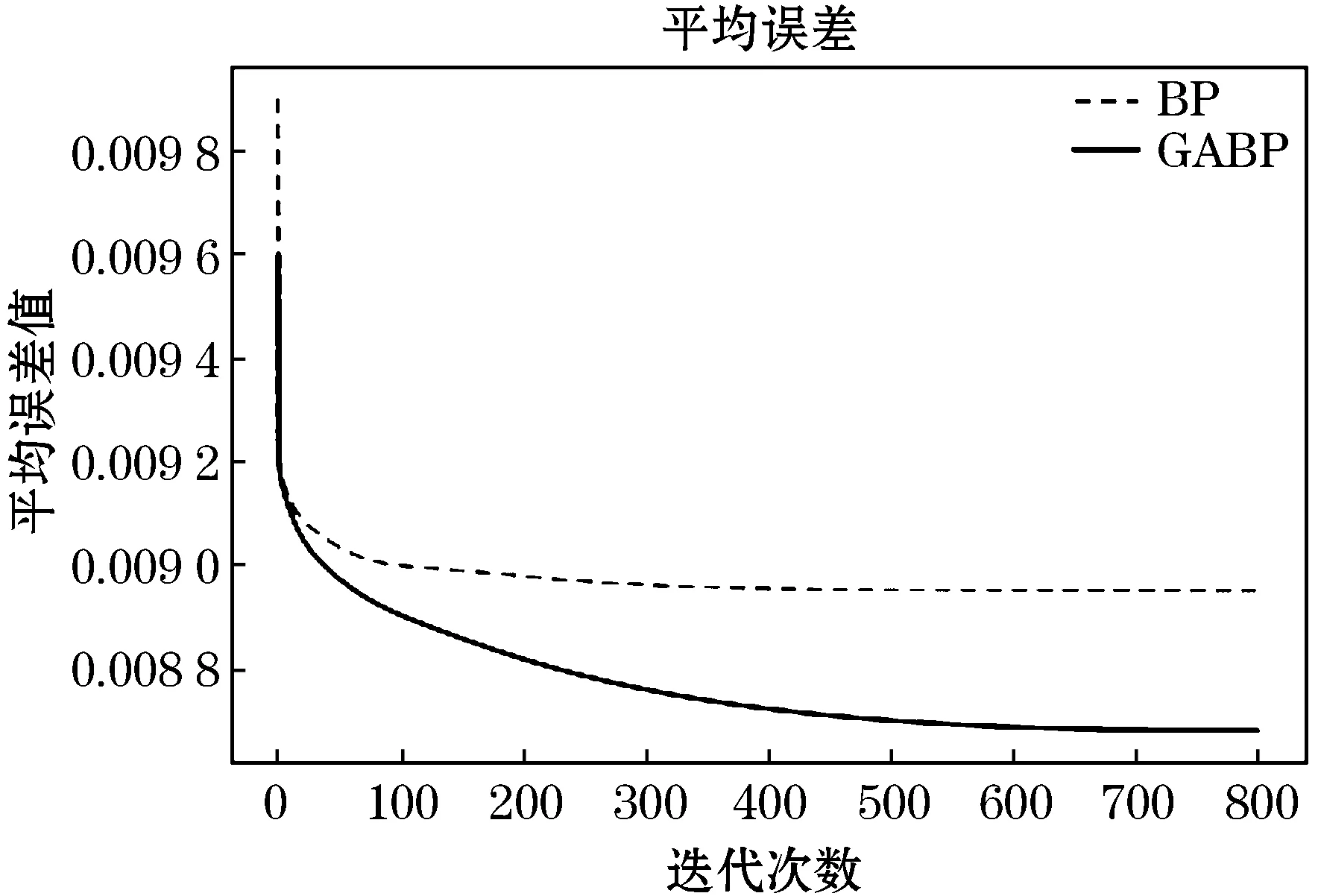
图3 BP与GA-BP训练结果比较

表2 神经网络在改进前后的平均误差对比

由表2可知，相对于常规的BP神经网络的平均误差0.681 71%，自适应遗传算法优化BP神经网络对白葡萄酒的预测结果的平均误差为0.665 68%.图4是反映了两种模型的泛化能力，由此可知GA-BP模型的泛化能力要高于BP模型的泛化能力，且GA-BP模型的精确度也是高于BP模型的.

图4 BP与GA-BP仿真预测比较

4 结 语

神经网络是目前较为流行的一种智能算法，因为神经网络在处理非线性系统问题的出色能力而被广泛应用，但还存在着一些缺陷.本文通过自适应遗传算法优化神经网络的权值和阈值，并且还自适应调整了学习率，提高了模型的准确率及泛化能力.建立了GA-BP模型，并将模型用于白葡萄酒的质量评价，通过仿真结果的比较，GA-BP模型比传统的BP模型具有更好的泛化能力.企业聘请资深的品酒员对葡萄酒进行评价不是一件容易的事，而且对于品酒员来说，存在的主观原因可能会对评价结果造成差异.本文构造的GA-BP模型为葡萄酒的质量评价提供了一个参考方式，同时对其他食品加工企业有一定的借鉴.