思想的绽放

李平龙

【摘要】数学思想是小学数学的重要内容，以恰当的方式进行板书设计，能帮助学生更好地理解知识，掌握和理解相应的数学思想，达到渗透数学思想的目的.直观板书能渗透数形结合思想，合理板书能渗透模型思想，有序板书能渗透归纳推理思想.

【关键词】小学数学;板书;数学思想;渗透

小学数学课程标准中明确提出：通过义务教育阶段的数学学习，学生能够获得适应社会生活和进一步发展所必需的数学的基本知识、基本技能、基本思想、基本活动经验.这充分说明了数学思想在数学学习中的重要性.数学思想是从数学内容中抽象概括出来的，它既是数学知识的精髓，又是知识转化为能力的桥梁.在小学阶段，数学思想方法主要有数形结合思想、模型思想、归纳推理思想、集合思想、函数思想、统计与概率思想等.在小学数学阶段有意识地向学生渗透一些基本的数学思想，可以加深学生对数学概念、公式、法则、定律的理解，提高学生解决问题的能力和思维能力，是小学数学进行素质教育的真正内涵所在.

课堂是教师向学生渗透数学思想的主阵地.在小学数学课堂中渗透数学思想的方法和策略非常多，很多专家和一线教师都有丰富的研究成果，但大都是从教材处理和组织学生活动等角度出发的.而在数学课堂中，板书是不可或缺的重要组成部分，它呈现了一节课中教学的精华，体现了教师的教学智慧.因此，我在参考了许多专家和老师的研究成果的基础上，思考着从课堂板书这个角度渗透数学思想.我在进行了一些探索和思考后发现，在充分发掘教学素材中的数学思想的基础上，以各种恰当的方式进行板书，也能帮助学生更好地理解知识，掌握和理解相应的数学思想，达到渗透数学思想的目的.

一、数形互助，直观板书，渗透数形结合思想

数形结合思想就是通过数和形之间的对应关系和相互转化解决问题的思想方法，它在小学数学教学中有非常广泛的应用.数学家华罗庚曾说过：“数缺形时少直觉，形少数时难入微.”这句话揭示了数和形之间的辩证关系以及数形结合的重要性.在教学中，我们可以借助简单的图形、符号和文字相结合的示意图，促进学生形象思维和抽象思维的协调发展，沟通数学知识之间的联系，从复杂的数量关系中凸显数学的本质特征.这种思想方法可以借助板书直观呈现.

（一）利用板书以形得数

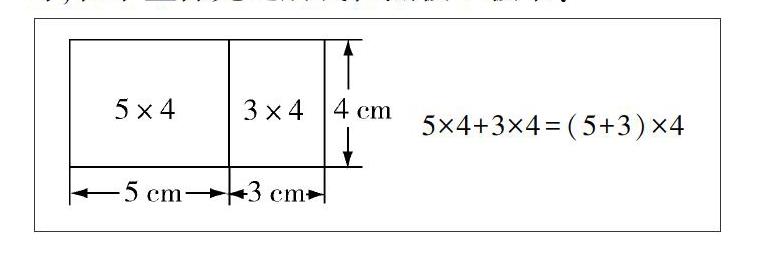
“形”具有形象、直观的优点，它能呈现更具体的思想，帮助学生理解较抽象的数量关系，因此，我们可以从“形”出发，找到相应的“数”，通过板书呈现的方式，帮助学生以“形”思考“数”，得到较好的教学效果.如在教学“乘法分配律”时，在学生探究之后我在黑板上板书：

5×4+3×4=（5+3）×4

如果只是板书右边的算式，学生通过计算只是知道了5×4+3×4和（5+3）×4的结果相等，而有了左边图形的帮助，学生可以直观地看到：左边长方形面积+右边长方形面积=整个图形面积，而5×4是左边长方形的面积，3×4是右边图形的面积，（5+3）×4是整個图形的面积，因此，就可以利用直观的图形理解抽象的算式.在此基础上，我继续修改上面板书中的数值，如把5改为6，3改为4，4改为5等，让学生理解这个式子的一般性，学生从这个动态的板书中就能很好地理解乘法分配律的本质意义，既掌握了乘法分配律的推导过程，又体会了数形结合思想在学习中的作用.

（二）利用板书以“数”想“形”

“形”虽有直观的作用，但必须有准确抽象的“数”加以确定才能体现数学的严谨性，特别是一些比较复杂的情况下，以“数”定“形”更为重要.如教学六年级下册“数学思考”例5：6个点可以连成多少条线段？8个点呢？

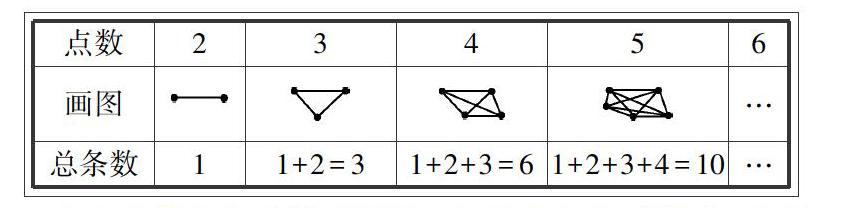
我先让学生尝试画一画，学生在经历了画和数的过程之后，我根据学生的反馈板书如下：

为了让学生准确找出规律，我让学生从“形”入手，从2个点可以连1条线段开始，依次递增1个点，再数出得到的线段条数（以“数”定“形”）：2个点连成1条线段;3个点连成线段的条数：1+2=3（条）;4个点连成线段的条数：1+2+3=6（条）;5个点连成的线段条数：1+2+3+4=10（条）……规范的板书能让学生直观而清晰地看到点数与线段总条数的构成情况及规律，通过各种颜色的线段区分增加条数的情况，再把增加的条数和图形对应起来，就能清晰地呈现知识的形成过程，让学生体会到数形结合的魅力.

二、理清本质，合理板书，渗透模型思想

数学模型是用数学语言概括地或近似地描述现实世界事物的特征、数量关系和空间形式的一种数学结构.郑毓信教授在对新课程标准的解读中也说到，新课程标准提倡数学基本思想的真正新意，在于对一些新的理论思想的突出强调.模型思想是一般化的思想方法，伴随着数学知识的产生和发展，模型思想也在不断地发展.但小学生还处于形成模型思想的起始阶段，对于较复杂的模型情况比较难于理解，如果教师能把抽象的模型思想直观地板书出来，对学生将有很大的帮助.

如在一次数学老师招考面试中，我一共听了30位老师讲四年级上“积的变化规律”的导入和新授环节，这个环节需要让学生理解“一个因数不变，另一个因数乘（或除）以几，积也乘（或除以）几”.这里面既有函数的数学思想，也有一个建立模型的过程.大部分老师都突出强调了“一个因数不变”“另一个因数乘或除以几”“积也乘或除以几”“几是相同的数”这四个方面，而缺乏建立模型的过程.但有一位老师与众不同，她通过求一个长10厘米、宽2厘米的长方形面积开始，不断增加宽的长度，得出相应的算式，并板书如下：

……         ……

一个因数不变，另一个因数乘（或除以）几，积也乘（或除以）几.

其中的“几”是很有讲究的，因为这个“几”能代表除0外的任何有理数，在这里要让学生理解除0外的所有自然数（以后再扩展到小数和分数），而大部分老师只是讲了“几”代表“2，5，10，100”这些数，但这位老师从算一个长10厘米、宽2厘米的长方形面积导入，再把宽增加到4厘米、6厘米、8厘米，也就是将其中一个因数乘2，3，4，…，然后在这个基础上继续引导学生完成推导，得出最终的结论.这位老师挖掘了教材中的模型思想，通过板书呈现了整个模型建立的过程，既有利于学生对数学知识的理解， 又对学生模型思想的发展具有现实的意义.

三、简洁呈现，对比板书，渗透集合思想

集合思想在小学数学的很多内容中都有渗透，在一年级学习之初，学生在认数和分类等知识中就已经有所接触，一直到高年级学习公因数和公倍数、三角形和四边形的分类、数的分类（正数、0、负数）等，不同年级和不同知识领域都有所渗透.但是集合的知识并不是小学数学的必学内容，因而应注意把握好知识的难度和要求，尽量使用通俗易懂的语言渗透集合思想.因此，简洁直观的板书非常有利于渗透集合思想.

如在教学“四边形的分类”一课时，为了让学生正确地理解分类，我们可以在学生探究的基础上呈现如下板书：

学生根据板书做进一步解释：平行四边形、长方形、正方形、梯形都属于四边形，长方形是特殊的平行四边形，正方形是特殊的长方形，梯形中有等腰梯形和直角梯形两种特殊形式.这样，板书简洁直观地呈现了四边形的分类问题，让学生在掌握相关知识的同时初步了解了集合的思想.

又如：六（1）班举办文艺活动，表演舞蹈的有19人，表演小品的有12人，两类节目都参加的有5人.该班共有多少人参加这两类节目的演出？

分析：为了便于学生理解，我们借助Venn图来板书.左边的圈是一个整体（集合），表示表演舞蹈的人，右边的圈表示另一个整体（第二个集合），表示表演小品的人，两个圈相交的部分表示特殊的整体（交集，也是第三个集合），表示两类节目都表演的人.这样的直观图板书，可以很容易地帮助学生理解：该班参加这两类节目演出的人数是19+12-5=26（人），同时让学生体会到了集合的思想.

四、几何直观，有序板书，渗透归纳推理思想

推理是重要的思想方法之一，是数学的基本思维方式，它贯穿于小学数学教学的始终.而类比和归纳是小学数学教学中常用的推理思想，特别是不完全归纳法，在小学数学教学中的应用非常广泛.小学数学中很多运算法则、公式、定律等的推导，都是在列举几个具体例子的基础上得出的.如果教师能利用几何直观的方法，有序地板书相应的内容，则能顺利地达成教学目标，同时向学生渗透相应的归纳推理思想.

在教学二年级“排列组合”时，有这样一个问题：用1，2，3能组成哪几个两位数？在听一位老师上课时，我看到她的方法是：先在黑板上写好个位、十位，然后在下面依次去写数字，组成6个两位数，然后让学生说一说组数的过程和顺序.通过巡视课堂和课后交流，我发现大半学生都能掌握这一知识.

但我在听课的过程中发现，有部分学生会出现重复或遗漏的情况.在我们成人看来，这样已经讲解得非常清楚了，为什么还会出现这样的情况呢？通过进一步的思考和分析，我发现：虽说这位老师注意到了写数的顺序，先確定个位或十位，板书也是按照这个顺序呈现的，但这更注重结果的呈现，思维过程不够直观.究其原因有两点：一是二年级学生的思维水平是比较低的，我们成人觉得十分简单的过程在他们眼中并不简单，因此，不能用成人的思维类推他们的思维;二是在学生的眼中这样的图还不够直观，特别是这个图不能直观地反映“取数”的顺序和“组数”的过程.后来在教学中我采用另一种直观的几何图示来尝试解决这个问题，图示如下：

结合上面的图，我让学生边画边说，先取1，剩下2和3，能组成12和13;再取2，剩下1和3，能组成21和23;最后取3，剩下1和2，能组成31和32.当我把数字1，2，3换成3，5，7时，学生照样能自己排列出来.通过尝试，我发现所教班的48个学生不仅很喜欢这种直观画图的方式，而且都掌握了组数的方法，在后面的练习中极少出错.因此，通过恰当的几何直观的方法有序板书，能直观呈现思维的过程，帮助学生深刻地理解数学知识与方法.

综上所述，如果教师能深入地理解数学知识，挖掘其中的数学内涵，设计好相应的板书，就能顺利达成教学目标，还能渗透相应的数学思想，起到事半功倍的效果.

【参考文献】

[1]王永春.小学数学思想方法梳理（一）[J].小学数学教育，2010（1）.

[2]朱秀英.例谈小学数学中的思想方法[J].中国教育技术装备，2009（07）： 109.

[3]郑毓信.《义务教育数学课程标准（2011年版） 》另类解读 [J].数学教育学报，2013（1）.