时滞混沌系统的有限时间容错同步控制
李 强,张悦娇
(北京科技大学天津学院 基础部,天津 301830)
0 引 言
近些年,混沌系统同步的研究得到了越来越多国内外学者的重视。因为随着信息现代化步伐的加快,很多重要的信息需要被安全地传递,利用混沌系统的同步可以使信息通过加密—传递—解密的方式,安全准确地进行传递。因此,混沌同步在通信加密领域有着十分广泛的应用[1-2]。
随着对驱动-响应混沌系统同步的不断研究,出现了很多类型的混沌同步方式,如渐近同步[3]、完全同步[4]、投影同步[5-7]、脉冲同步[8],然而这些文献中的同步研究并没有考虑时滞问题。之后,文献[9]利用滑模控制的方法研究了具有时滞的混沌系统的组合同步[9]。利用脉冲控制方法[10]R.C.Wu[10]对时滞混沌系统的延迟同步问题进行了研究。文献[11]和[12]分别针对2个时滞混沌神经网络的间歇同步和时滞混沌系统投影同步控制问题进行了分析。
在实际应用中,往往希望同步收敛的时间越短越好,这样可以节约生产成本并且提高经济效益,因此具有收敛速度更快、鲁棒性更好的有限时间同步控制方法被应用在混沌系统同步的研究中。例如文献[13]研究了2个具有时变时滞混沌神经网络的有限时间同步控制问题。不同于文献[13],文献[14]讨论了具有时变时滞和有界扰动的混沌系统的有限时间同步控制问题。由于系统部件老化、环境不稳定等各种因素,系统会出现卡死故障或者是一部分执行器失效的问题。而这些文献中都没有考虑系统在长期运行中出现故障的情况。
基于上述分析,本文研究了时滞混沌系统的自适应有限时间容错同步控制问题。主要的创新点如下:1)具有时变时滞并且结构不同的驱动-响应混沌系统被研究;2)考虑混沌系统出现未知的卡死故障和部分执行器失效的情况,设计自适应故障容错控制器,其中自适应增益更新率实现了对误差系统实时有效的控制;3)利用李雅普诺夫稳定性和有限时间稳定性定理,得到误差动态系统同步的过渡时间。
1 问题描述
考虑具有时变时滞的混沌系统模型如下所示:
(1)
其中,A1∈Rn×n表示系统矩阵,x(t)=[x1(t),x2(t),…,xn(t)]T∈Rn表示混沌系统(1)的状态向量;f1(x(t))∈Rn和g1(x(t-τ(t)))∈Rn表示连续的非线性函数向量,且f1(0)=g1(0)=0,τ(t)表示时变时滞。
基于驱动-响应同步的概念,将系统(1)作为驱动系统,与其对应的响应系统如下所示:
(2)
其中,A2∈Rn×n表示系统矩阵,y(t)=[y1(t),y2(t),…,yn(t)]T∈Rn表示状态向量;f2(y(t))∈Rn和g2(y(t-τ(t)))∈Rn表示连续的非线性函数向量,且f2(0)=g2(0)=0,u(t)∈Rn表示控制输入向量。
考虑系统可能出现故障的情况,根据文献[15]将故障容错控制器描述如下:
uF(t)=vu(t)+δ(t)
(3)
其中,uF(t)是故障执行器,v是未知的执行器效率因子,且δ(t)表示未知的时变有界信号。
根据上面的故障容错模型,具有执行器故障的响应混沌系统模型描述如下:
(4)
定义同步误差e(t)=y(t)-x(t), 因此同步误差动态系统表示如下:

(5)
为了进一步的研究,给出了如下的定义、引理和假设。
定义1[16]如果存在一个常数0 并且 ‖y(t)-x(t)‖=0,∀t>t0+T 则称驱动系统(1)和响应系统(2)是有限时间同步的。 引理1[17]假设V(t)是连续的正定函数,且满足以下微分不等式条件: 其中,ω>0和ι∈(0,1)为常数。那么,对于任意给定的t0,V(t)满足以下不等式: V1-ι(t)≤V1-ι(t0)-ω(1-t)(t-t0),t0≤t≤t1 并且 V(t)≡0,t≥t1 其中 引理2[18]如果a1,a2,…,an,r,p为实数且满足0 假设1存在常数l1,l2>0,使得 ‖fi(u)-fi(v)‖≤l1‖u-v‖ ‖gi(u)-gi(v)‖≤l2‖u-v‖ 其中i=1,2,u,v∈Rn,u≠v。 为了使得驱动-响应混沌系统能够在有限时间内达到同步,设计了如下的自适应容错控制器 (6) 其中,0<μ<,α1是大于零的任意常数。 设计的控制器增益的更新率为 (7) 其中Ω=l1[‖y(t)‖+‖x(t)‖]+l2[‖y(t-τ(t))‖+‖x(t-τ(t))‖],l1,l2,β,α2是大于零的任意常数。 定理1 在满足假设1和假设2的条件下,自适应容错控制器(6)和更新率(7)能够保证时滞混沌系统是有限时间同步的,并且过渡时间 (8) 证明:选取李雅普诺夫函数如下 V(t)=V1(t)+V2(t) (9) (10) 计算V1(t)沿系统(5)的导数及自适应控制器(6),有下式成立: +g2(y(t-τ(t)))-g1(x(t-τ(t)))+vu(t)+δ(t)} ≤eT(t)[A2y(t)-A1x(t)]+eT(t)f2(y(t))-eT(t)f1(x(t)) +eT(t)g2(y(t-τ(t)))-eT(t)g1(x(t-τ(t)))+eT(t)vu(t)+eT(t)δ(t) ≤eT(t)f2(y(t))-eT(t)f1(x(t))+eT(t)g2(y(t-τ(t)))-eT(t)g1(x(t-τ(t))) (11) 由假设1可知 eT(t)f2(y(t))-eT(t)f1(x(t))≤‖eT(t)‖‖f2(y(t))-f1(x(t))‖ ≤‖eT(t)‖l1[‖y(t)‖+‖x(t)‖] (12) 类似地,可得 eT(t)g2(y(t-τ(t)))-eT(t)g1(x(t-τ(t)))≤‖eT(t)‖‖g2(y(t-τ(t)))-g1(x(t-τ(t)))‖ ≤‖eT(t)‖l2[‖y(t-τ(t))‖+‖x(t-τ(t))‖] (13) 结合式(11)、(13),可得 -k(t)eT(t)e(t)-α1eT(t)φ(t) =‖eT(t)‖Ω-k(t)eT(t)e(t)-α1eT(t)φ(t) (14) 计算V2(t)的导数,结合自适应更新律(7),有下式成立: (15) 结合式(14)、(15),可以得到 因此 (16) 通过引理1,可以得到当t≥T*时,V(t)=0, 即误差系统(5)在控制器(6)的作用下是有限时间稳定的,这里T*满足(8)式 本小节给出算例仿真验证所设计的自适应容错控制策略的有效性。 考虑2个不同的具有时变时滞的混沌系统Lorenz系统和Chen系统: 根据所设计的自适应控制器和自适应更新率,选择参数如下:取μ=0.51,α1=1.1,α2=1,β=1.2,l1=l2=1,时滞τ(t)=et/(1+et). 选择系统的初始条件分别为(x11(0),x12(0),x13(0))=(1,-1,1),(x21(0),x22(0),x23(0))=(2,1,0), 自适应控制器增益的初始条件为k(0)=1,图1~2分别是Lorenz系统和Chen系统的开环状态轨迹,从图1~2中可以看出2个系统具有混沌现象。 图1 Lorenz系统的状态轨迹 图2 Chen系统的状态轨迹 图3 同步误差的变化轨迹 图4 控制增益的变化轨迹 同步误差系统的轨迹如图3所示。从图3可以看出,在t=6 s之前,误差系统在所设计的有限时间自适应控制器的作用下很快到达了平衡点,即驱动-响应混沌系统很快实现了同步;在t=6 s之后,由于系统突然出现了未知的卡死故障和执行器的部分失效,导致同步误差偏离了平衡点,但是在容错控制器的作用下,很快又收敛到平衡点,这说明所设计的容错控制器是有效的。同时图4给出了控制增益的相应变化轨迹。 本文研究了具有时滞混沌系统的有限时间同步容错控制问题。考虑混沌系统具有时变时滞和出现故障问题,设计了相应的自适应容错控制器。控制增益很好地实现了对误差系统的实时控制,并且保证了执行器出现故障时,所设计的控制器能够对闭环系统有效控制,此外还得到了有限时间同步的过渡时间。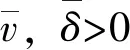
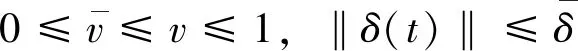
2 主要结果


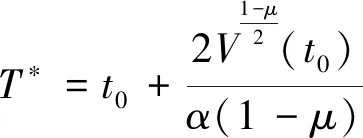






3 数值仿真



4 结 论

