空间圆柱形物体变形的检测方法

杨 丽

(上海市城市建设工程学校(上海市园林学校),上海 200232)

对于空间圆柱形物体，在实际和设计时会存在差异，或者是在长期使用后会发生形变而影响其使用情况。因此必须对空间圆柱体进行检测，判断其是否满足工程要求[1]。

1 观测及算法原理

1.1 数据采集

本文中的观测目标为空间圆柱形，所以整个物体的观测数据必然不能在一个测站上全部测得。因此，首先需在物体周围选择2个合适的地点作为测站，这样就形成了2个自定义的坐标系，接下来还必须选定4个公共点，便于后期数据的整体处理。

1.2 数据拼接算法原理

不同测站观测的坐标属于不同的坐标系。但如果在不同的测站观测一些公共点就可以将这些点的坐标归算到1个坐标系(图1)。

图1 不同测站的2个坐标系

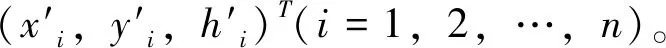
公共点之间的关系表示为

(1)

式中的(x0，y0，h0)为平移量，R1(α)、R2(β)、R3(γ)为旋转矩阵

当公共点个数n大于3时，可以按最小二乘求定以上6个参数。对每个公共点，列出误差方程为

(2)

式中的V=(VxVyVh)T为转换残差(改正数)。

(3)

(3)式中偏导数和常数项

根据上述过程，利用各个测站观测的公共点，可以将所有观测值统一到1个坐标系中，相当于在1个测站观测到了整个物体的表面。

1.3 模型拟合算法原理

如图2所示，圆柱的半径为R，过观测点Pi作与圆柱面轴线垂直的平面，其与圆柱轴线的交点为P,直线PiP与圆柱面的交点为P′。显然可以用偏离距离PiP′作为残差,列误差方程[1]。

图2 圆柱体的拟合模型

设中心轴线方程为

(4)

式中(a，b，c)T的为空间直线的单位方向矢量，(x0，y0，h0)T为中心轴线与xoy平面的交点，t为直线上任意点至(x0，y0，h0)T的距离。为了唯一表示直线，定义a>0。若a=0，则b>0；若a=0且b=0，则c>0(a、b、c不可能同时为0)。

过观测点Pi(xi，yi，hi)与中心轴线垂直的平面方程[2-3]

ax+by+ch+Di=0

(5)

其中Di=-(axi+byi+chi)

将轴线方程代入平面，求得

t=-(ax0+by0+ch0+Di)=a(xi-x0)+b(yi-y0)+c(hi-h0)

(6)

中心轴线与该垂直面的交点坐标

(7)

各点的误差方程为

(8)

将误差方程线性化为

(9)

其中

写成矩阵形式

Vi=Aiδx-Li

(10)

其中δx=[δa，δb，δc，δx0，δy0，δh0，δR]T。此时a,b,c需满足条件a2+b2+c2=1，即

aδa+bδb+cδc=0

(11)

按附有条件的平差方法平差，但显然条件方程式不能使得(abc)T满足和a>0的要求[4-5]。平差迭代步骤为

(2)按照误差方程式(10)和条件方程式(11)得到法方程为

(12)

求解得到参数的第一次改正数δx(1)，未知数修正为a(1)，b(1)，c(1)，x0(1)，y0(1)，h0(1)，R(1)。

(3)若第k次迭代求得未知数为a(k)，b(k)，c(k)，x0(k)，y0(k)，h0(k)，R(k)，将(a(k)，b(k)，c(k))T单位化

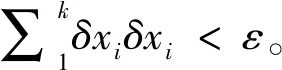
2 算例分析

本例中数据来源于某建筑物前的柱子(图3)。

图3 某建筑物前的圆柱体

设置了2个测站，测站1和测站2，设置测站1和测站2时分别用全站仪测量A、B、C、D 4个公共点，以供坐标转换时用。

其中测站与公共点的布设关系如图4所示。

图4 测站与公共点的布设关系

表1为观测圆柱体时坐标转换的公共点数据。

表1 公共点数据 m

表2为测站1坐标转换到测站2坐标系。

表2 测站1坐标转换到测站2坐标系 m

转换后的数据如图5所示。

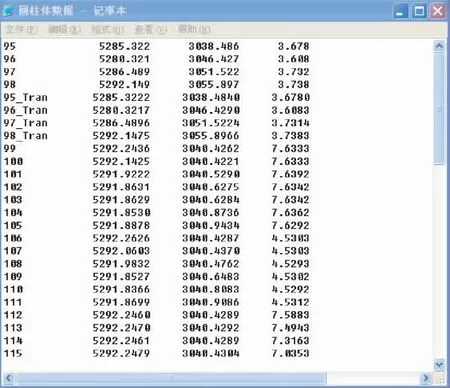
图5 坐标转换后的数据

坐标转换后，进行数据拟合。读入数据对其进行拟合，得出中心线方程即圆柱体的拟合结果，如图6所示。

图6 拟合结果

至此，拟合结束。点“残差”按钮，显示拟合的残差，残差见表3。

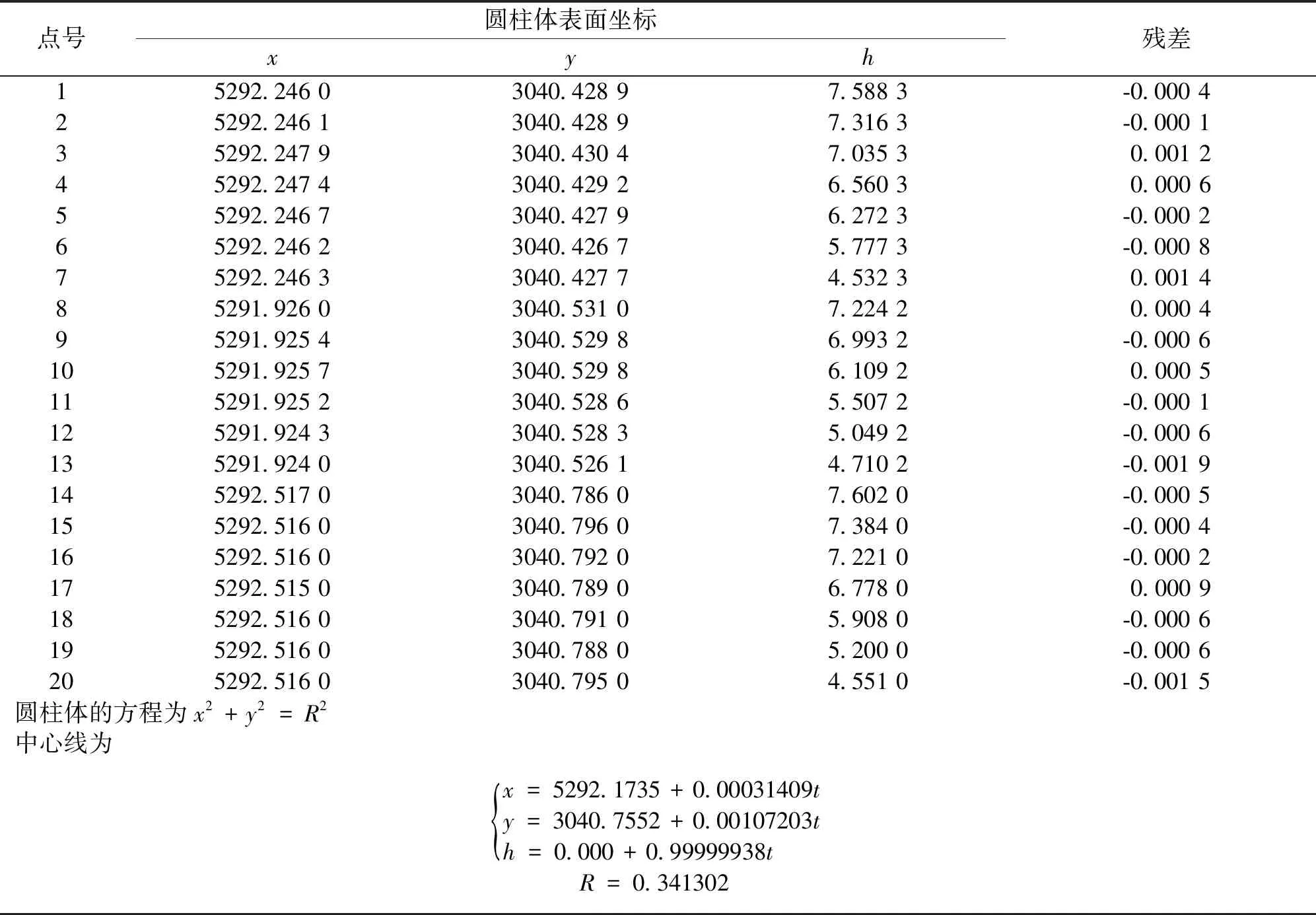
表3 拟合圆柱面坐标与残差 m

程序可以连接AtuoCAD，根据圆心坐标和半径可以画出圆柱体立体图，并通过语句“shademode”+“_3D wireframe”实现着色，效果如图7所示。

图7 拟合的圆柱体图形显示

3 结 论

本文介绍了空间圆柱体的检测方法，利用全站仪观测物体表面点的空间坐标，拟合出圆柱体的方程，将拟合出的中心线方程、半径与设计时对比，即可得出圆柱体的整体变形情况，根据每个观测点的残差情况，即可看出每点的变形情况。从拟合的结果来看，此物体整体情况良好，没有变形特别明显的点位。