二维串置翼型气动特性数值分析

王昀皓， 朱文武， 张昕喆， 代 君

(郑州航空工业管理学院 航空工程学院， 河南 郑州 450046)

0 引 言

目前，针对低速下高升力无人机研究较少，故提出串列翼布局。在实际应用中，串列翼能比单翼提供更大的升力[1]，在短距起降、运输导弹和炮射布局[2]巡飞器中具有独特优势，并且已得到了广泛应用。与常规布局的飞行器相比，串列翼飞行器前后两个翼面都可以产生升力，可以减少对机翼结构刚度要求和减小主翼面的翼展。然而，升阻系数的提高和升阻比变化规律很难预测，需要进一步深入探究。

已有研究表明[3-8]，串列翼前后翼产生的升阻特性并不相同，且前翼、后翼在大迎角下的升力变化是非线性的。文中在文献[1-3]研究的基础上做进一步探究，寻找串列翼布局升阻特性随不同参数的变化规律，对研究低速下大载荷飞行器具有重要意义。

文中参考了刘国庆等[9]非结构网格划分方法，使用商业软件ANSYS fluent作为仿真软件模拟，选用PRD3翼型作为基础翼型，用两段相同的翼型，通过改变不同的安装位置得到升力系数曲线。根据流场分析结果寻找翼干扰规律，并对后面的研究做出展望。

1 研究与方法

1.1 模型选择

机翼开缝产生新的翼型具有较大的相对弯度和厚度，在翼型选择时，PRD3翼型作为基础翼型。考虑到翼型后缘尖端较为明显，影响网格质量以及计算精确性，数值计算时自后缘截去14 mm，翼型及仿真相关参数见表1。

表1 基本翼型几何参数

两段翼的排列组合参数如图1所示。

图1 前后翼相对安装位置

以前翼未切后缘时的弦长c=0.25 m对该翼型外形参数量纲归一化后，后翼前缘点位置为(x/c，y/c)，后翼弦线与前翼弦线夹角α。令y=0.32c，取x=0、0.2、0.4、0.6、0.8、1.0共6组模型探究后翼相同高度下对总体升力的影响；再将前后翼视为一个开缝机翼，控制开缝机翼的总弦长不变，以后翼后缘点为旋转中心，取迎角α=2°、4°、6°、8°、10°、12°共6组模型探究缝道对总体升力的影响。

1.2 控制方程

文中模型飞行速度为10 m/s，流体运动速度不超过0.3马赫，故选用不可压流的运输方程，运输方程描述如下[10]:

1)连续性方程为

(1)

2)动量方程为

(2)

(3)

(4)

3)能量方程为

(5)

式中:ρ----密度;

t----时间;

Vx,Vy,Vz----X,Y,Z轴向速度，m/s;

E----能量，J。

1.3 边界条件设置

仿真工况为标准大气压，选取速度远场均匀来流，速度v取10 m/s。由于翼型排列相对位置和两翼翼弦夹角不同，导致最小和最大失速迎角不同，迎角计算到上下翼面出现明显气流分离为止。根据外部绕流计算域选取常规经验，流场尾迹区长度选择为翼型特征长度10倍以上，迎流区长度为5～8倍以上。创建前半圆r=4 200 mm、后矩形d=8 400 mm的区域，作为模型流场计算区域。流域上、前、下三个面设置为速度入口边界条件，尾流区域大于30倍特征长度后边界面设置为outflow。

在翼型附近建立矩形加密区域，加密迎流区长度4倍弦长，加密尾流区5倍弦长，加密上下宽度两倍弦长。翼型附近网格加密区如图2所示。

1.4 网格划分

使用Icem网格划分软件，对计算域流场进行有限单元非结构化网格划分。选用非结构二维网格，在使用同样单段翼模型下进行网格划分，网格规模分别为4 W、6.4 W、8.1 W、9.6 W，区别在于内部加密区域网格密度，如图3所示。

图2 网格加密区局部示意图

图3 不同规模网格升力系数

当网格数目选择9.6 W时，可满足数值计算

精度，故选用9.6 W时的网格设置使用文中的所有模型。提取壁面附近y+分布，最大值均小于10，附面层网格满足所选湍流模型。

2 结果与分析

2.1 后翼横向安放位置对升阻系数影响

前翼和后翼在不同安装位置升阻系数变化规律如图4所示。

根据以往串列翼安放位置经验[3]，纵向翼间距y取正值都能达到增升的效果，y值较小，可视为机翼开缝；y值较大，则增生效果不明显。在y/c=0.32时，x取不同值的最大升力阻力系数见表2(参考特征长度为单翼长度)。

表2 后翼不同横向位置安装对比

(a) x/c=0 (b) x/c=0.2

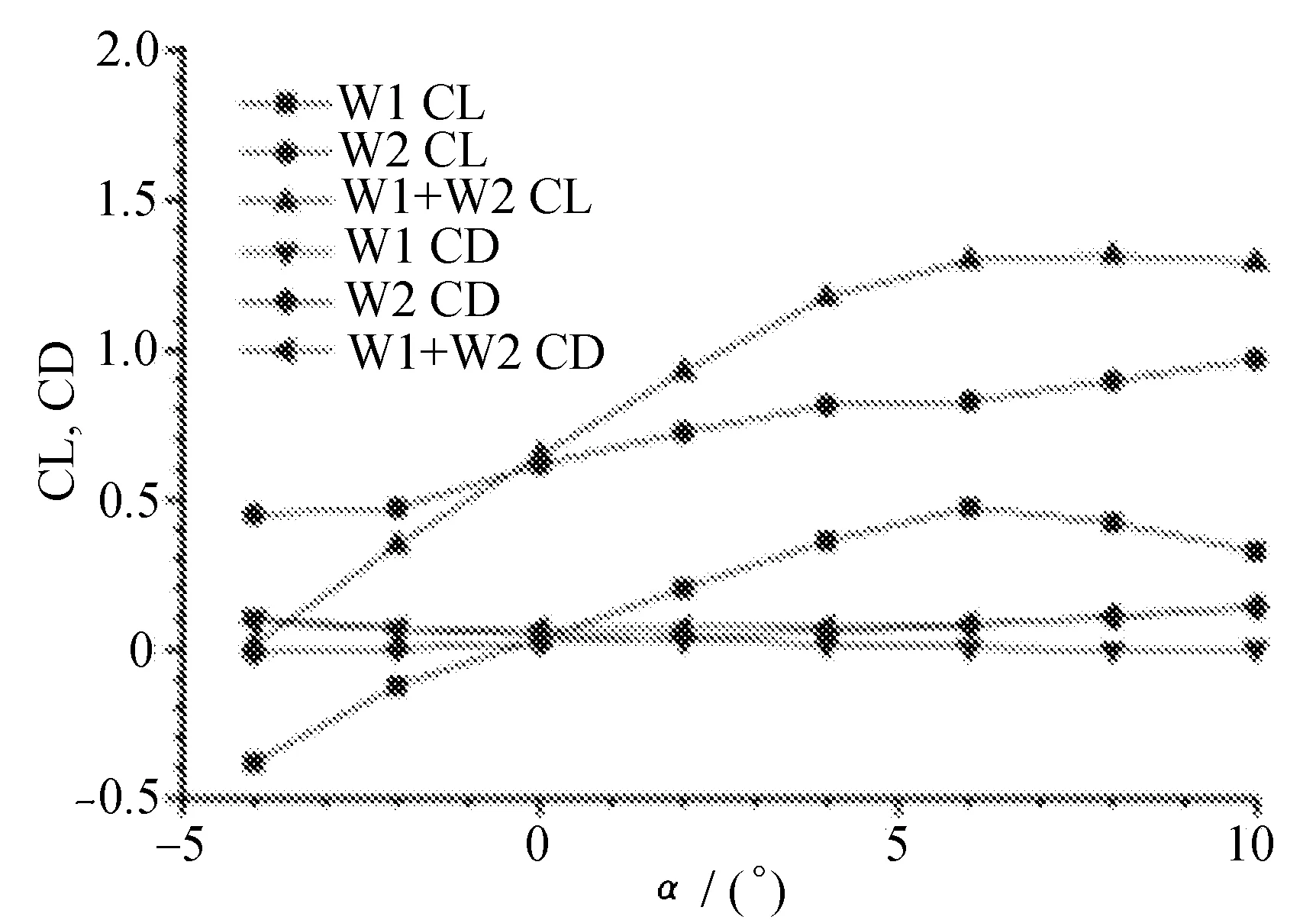
6种横向安装位置升力系数对比如图5所示。

图5 6种横向安装位置升力系数对比

由5可知，随着后翼的后移，增升效果在不断改善，在y/c=0.8和1.0时，升力曲线达到追平单翼×2的数据，并且在大迎角下具有更高的升力系数。x/c=0～1.0区间，后翼越靠后,增升效果越明显。

迎角为6°时流线图如图6所示。

查看来流迎角为6°时的流线图发现,相同迎角下串列翼前翼失速范围明显大于单翼，后翼失速范围小于单翼，推测原因是在后翼的下洗尾流影响下，对后翼上表面的气流分离有抑制作用，但对前翼上表面后缘的气流分离有增大的趋势。

迎角为6°时流场静压分布如图7所示。

图7是迎角为6°时单翼和串列翼在x/c=0.8时的压力云图，后翼的存在改变了整个流场的压力分布，使前翼上下表面压强差增大，进而使前翼升力上升明显。由于两机翼间的缝道呈收敛型，前翼下部受到来自缝道压缩流体向来流方向和向上的压力，同样这部分力传导到后翼上表面。对外显示为前翼升阻效率提升，而后翼效率降低，但总体效果好坏视后翼安装位置而定。

图6 迎角为6°时流线图

图7 迎角为6°时流场静压分布

2.2 后翼安装角对升阻系数的影响

α不同时前后翼升力系数变化如图8所示。

在两段翼距离近的情况下，可将串列翼视为一个整体的开缝机翼。取x/c=0.6，y/c=0.32的安装位置为基准，以前翼前缘到后翼后缘为开缝机翼的弦长。以后翼的后缘点为圆心旋转后翼，α取不同值时升力阻力系数见表3。

表3 后翼不同安装角对比

(a) α=2°(b) α=4°

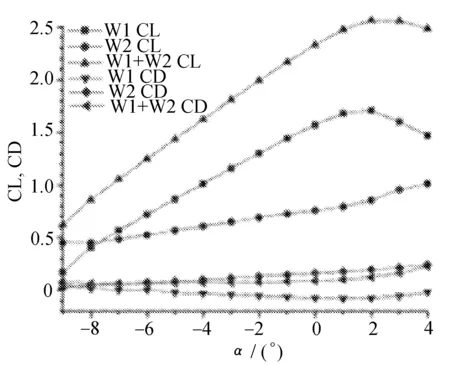
对比α不同时前后翼升力系数变化，前翼在达到失速迎角后升力系数下降，但后翼升力系数还在增长，整体升力系数下降较慢。

对比α=2°和α=12°的前后翼升阻曲线，发现2°时前翼失速后,后翼升力系数加速上升，而12°时前翼失速后,后翼升力系数几乎不变化，推测原因是12°时前翼与后翼同时接近失速状态。

在小迎角下，前翼上表面气流流速明显大于下表面流速，且受到收敛缝道影响，前翼可出现负阻力的现象。

不同相对安装角升力系数对比如图9所示。

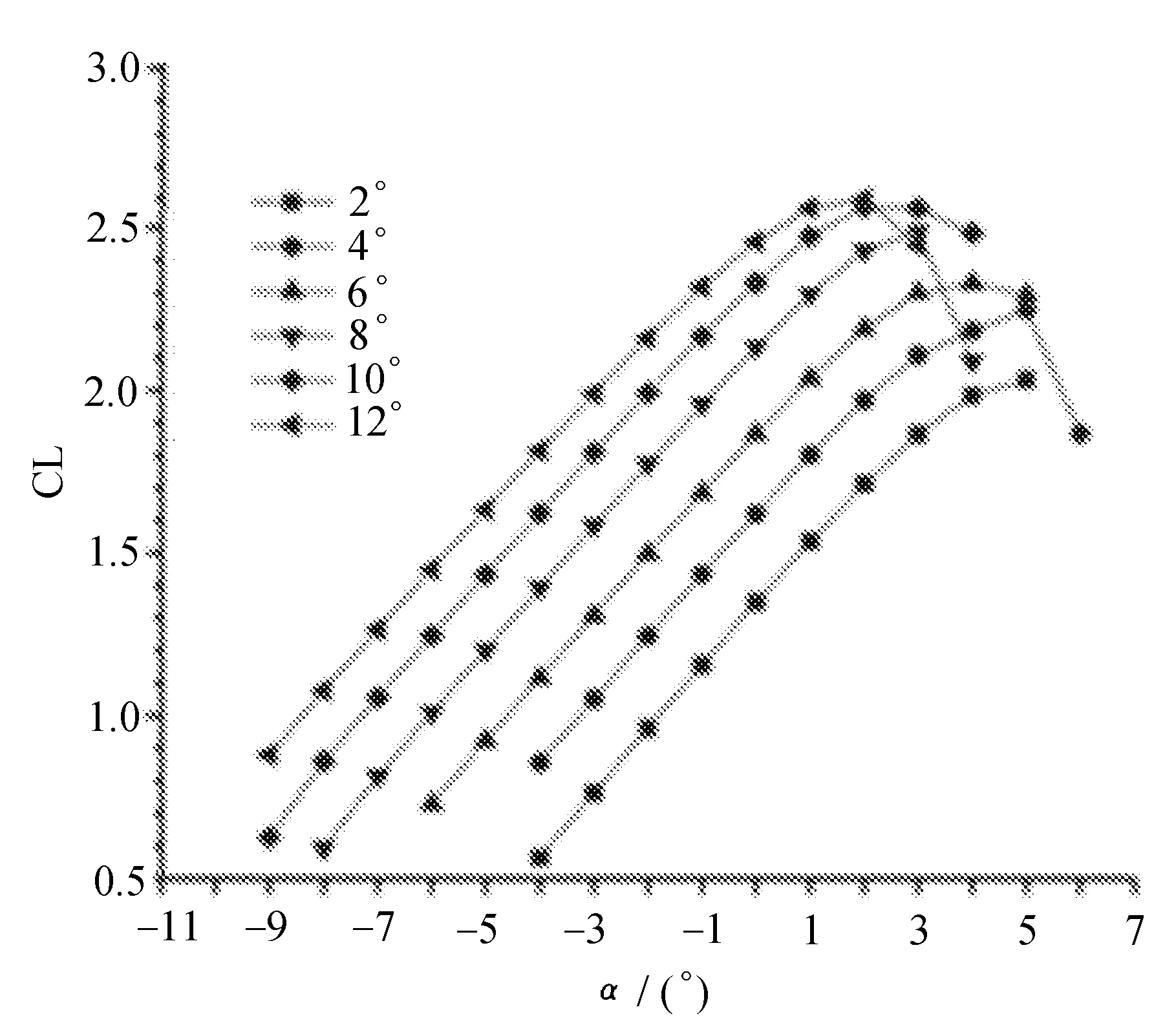
图9 不同相对安装角升力系数对比

由图9升力曲线对比可知，在α∈(0，12)时，α越大,开缝机翼的最大升力系数越大，到12°时最大升力系数达到最大。

不同安装角升阻比对比如图10所示。

由图10升阻比对比可知，α越大,升阻比曲线变化越平缓，即具有更宽泛的攻角适应范围，最大升阻比先增大后减小。在α∈(10，12)时，开缝机翼最大升力系数达到最大值2.589，比单翼最大升力系数的两倍即1.887,提升了37.2%，此时阻力系数增大了81.18%。

图10 不同安装角升阻比对比

图10中升阻比曲线随着后翼安装角的增大,先增大后减小，在安装角为8°时，获得最大升阻比达27。观察升阻比曲线可知,随着后翼安装角的增大，升阻比斜率越平缓。在后翼安装角为8°时，即获得最大升阻比，又有较高的升力系数。

x/c=0.32,y/c=0.6，来流迎角为2°时，不同后翼夹角下压力分布如图11所示。

观察图11攻角为2°时不同后翼安装角的压力云图可知，随着后翼安装角的增大，前翼上下表面压力差增大，10°～12°前翼上翼面压力基本不变。缝道过小会增大阻力，过大则增升效果不明显。

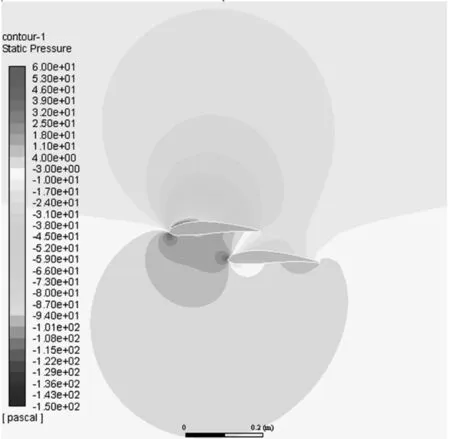
(a) α=2°(b) α=6°

(c) α=10°(d) α=12°

3 结 语

在串列翼优化过程中，合适的安装位置和安装角度对总体升力的提升有着极为显著的作用。这对于需要短距起降和大升力飞行器具有重要意义，主要结论如下：

1)对于串置翼型的简单排列，在保持垂直高差不变和后翼前缘不超过前翼尾缘的情况下，后翼越往后，增升效果越明显，相对来流迎角越大越明显。在垂直距离为0.32倍弦长时，最大升力系数相比于单翼最大提升8.1%。

2)对于串置翼型中前后翼的相对安装角，在控制等效的开缝机翼弦长一样的情况下，后翼的安装角在8°～12°能获得最优的排列方式。在选定的安装位置下，升力系数最大提升37.2%。

3)在一定角度范围内，后翼相对前翼的安装角α越大，升力系数曲线越平缓。但过大的安装角会导致升力系数最大值下降。

4)串列翼安装位置较近时，由于整体流场的作用，会使前翼升力系数大于单翼，后翼升力系数减小，阻力系数增加。

对低速下串置翼型的流场分布情况进行仿真，分析了串置翼型相比于单翼的优缺点。在今后的应用中，可以利用串列翼相互产生干扰的原理研发优化高升力、高阻力构型的飞行器，优化大载荷下飞行器的整体性能。此外，可以根据两段串列翼相互干扰的结论推导到多段串列翼的应用，完善和优化多段串列翼增升减阻的效果。