基于正余弦优化多阈值图像分割

张 睿， 刘 冰

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

0 引 言

近年来，基于模式识别技术的智能系统已被广泛应用于目标识别、人脸识别和计算机视觉等领域[1]。然而用于模式识别的图像可能会被设备或环境的噪声破坏，因此预处理阶段在图像处理过程中起着重要作用，而图像分割则是这一阶段的基本技术[1]。此技术根据对比度[3]、颜色[4]和亮度[5]将图像分割为不同的部分。许多方法已经实现了图像分割，如区域提取[6]、聚类算法[7]、直方图阈值[8]、边缘检测[9]和阈值分割[10]等。

在图像分割任务中，阈值分割(TH)是一种常用的图像分割方法，根据像素的强度等级，并根据一个或多个阈值将像素分割成不同的组[11]。阈值分割不仅简单而且鲁棒性好，可以处理有噪声的图像。根据图像所需的阈值数目，阈值分割可分为两类：双阈值处理和多级阈值分割[12]。在双阈值处理方法中，亮度值高于设定阈值的像素被标记为前景对象，其余像素则都被划分为背景对象[13]。而多级阈值分割(MTH)则使用多个阈值来分离代表图像中包含的多个对象区域中的像素。对于现实生活中的图像分割，最好的选择是使用多级阈值法。阈值问题可以概括为在图像上寻找最佳阈值。应该注意的是，阈值点取决于图像的直方图[14]，因此，每个图像都有自己的一组最佳阈值。

多级阈值分割技术通过多种方法寻找最优阈值,最常用的方法是分析图像的直方图。多级阈值分割具有一些挑战，例如确定阈值数量和执行时间。当阈值数目较少时，经典方法是合适的。但是，如果有大量的阈值,那么使用群体智能算法是一个好的办法。例如，粒子群优化(PSO)[15]、遗传算法(GA)[16]、蚁群优化(ACO)[17]、人工蜂群(ABC)[17]和Firey算法(FA)[17-18]。虽然这些方法在特定的图像分割场景中是有效的，但是每种方法都有其不足之处。因此，保证算法鲁棒性的一个有效方法是将这些方法混合在一起，使它们互相受益，同时避开单一算法的缺点。例如，研究人员提出一个混合模型FASSO[18-19]，将FA和SSO算法结合起来，在多级图像分割任务中对它们进行评估，FASSO算法节约了设备的计算时间，增强了SSO算法的搜索阶段。另一种名为WOAPSO算法[20-21]，使用whale优化算法(WOA)和PSO分别并行地更新种群；而种群被分成两部分，每个部分用其中一个算法更新，然后根据tent函数评估两个新解的合并。将WOAPSO算法在多级阈值分割问题上进行测试，其结果在PSNR和结构相似性指数(SSIM)方面优于其他算法。

针对前面描述的问题，研究尝试使用进化计算算法(ECA)作为新的解决方案。对于图像分割，研究人员使用Otsu或Kapur机制作为目标函数，寻找最佳阈值。在这种情况下，已有研究人员为多级阈值引入了几种ECA实现。这类方法的一些例子包括使用遗传算法(GA)[17]、粒子群优化(PSO)[22]、差分进化(DE)[23]、布谷鸟搜索(CS)[15,24]、风驱动优化(WDO)[25]、萤火虫算法(FFA)[4]、类电磁优化(EMO)[5]、社交蜘蛛优化(SSO)[5]、花授粉算法(FPA)[5]和乌鸦搜索算法(CSA)[5,17]等。而正余弦算法(SCA)[7]是最近提出的ECA算法，其在图像处理问题上的测试还鲜有报道。

SCA算法利用空间搜索和正余弦函数进行空间优化，考虑候选解决方案集的两个元素。其中一个选定的元素会影响另一个元素的下一个位置。正弦和余弦函数用于使用一些变量计算新位置，这些变量允许在两个数学运算符(正弦或余弦)之间切换。SCA已经在大量的基准函数上进行了测试，与类似方法相比显示出良好的性能。

综上所述，鉴于SCA还鲜有用于图像处理问题，文中目的可以概括为：

1)介绍基于SCA结合空间上下文信息的多级阈值分割方法；

2)在图像处理问题中，测试SCA算法的优化性能，并验证其有效性。

使用SCA多级阈值分割方法是根据每个图像的阈值数量生成多个最优解来实现的，使用不同的运算符来查找阈值的最佳配置。研究期望使用SCA算法结合图像上下文信息为多阈值图像分割提供新的解决方案。

1 方 法

1.1 Otsu-s多阈值分割

Otsu算法(最大类间方差法)是由日本研究人员于1979年提出的一种自适应计算二值分割阈值算法。在前景比较单一的图像中，该算法可以不受亮度和对比度的影响，实现较好的分割效果，因此在现阶段的图像预处理工作中得到了广泛应用。其核心思想是按照需求将感兴趣区域划分为前景，其他区域划为背景，前景和背景的类间方差最大处的阈值即为最优阈值。

假设I表示一张包含K+1个类别前景的灰度图像。如果想将图像分为CK(K=1，2，…,K+1)个子类，那么有必要确认K的阈值集合，用{t1，t2，…,tK}表示。进而得到

C0={I(i，j)∈I|0≤I(i，j)≤t1-1}，

C1={I(i，j)∈I|t1≤I(i，j)≤t2-1}，

CK={I(i，j)∈I|tK≤I(i，j)≤L-1}，

式中：I(i，j)----像素的灰度(i，j)；

L----I内不同灰度的数量。

多阈值法的目的是确定最佳阈值，该阈值通过最大化方程来确定，即Otsu-s函数，其具体公式如下：

(1)

(2)

(3)

(4)

式中:Pi----第i灰度级的概率;

h(i)----第i灰度级的频率;

φi----I的平均强度(t0=0，tK+1=L)。

文中用Otsu-s函数作为t函数,用于执行基于直方图形状的图像阈值自动分割。其工作是确定包含两类像素(如背景和物体)图像中的最佳阈值，以分离这些类别，并使类内方差最小化，从而有效地将背景和对象分开。

1.2 正余弦算法(SCA)

正余弦算法(SCA)是一种元启发式算法，它利用正弦和余弦的数学形式应用于优化问题。SCA通过生成各种随机解来启动优化过程，然后初始化迭代以获得最佳解。以最佳解为目标点。在继续迭代过程的同时，正弦和余弦范围根据它们的数学形式进行调整，以更好地利用搜索空间。如果满足停止条件，则停止迭代。SCA的数学表达式

(5)

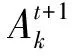
t----当前迭代次数；

n1，n2,n3----随机数；

Pk----第kth维度中的目标点；

n4----[0，1]区间内的随机数。

可以通过减小n1值来控制式中sin和cos的范围。

首先对每一步的SCA函数进行总结，然后生成一个随机种群的适应度。该算法确定全局最优解(目标点)，并基于目标点更新其余总体。此外，为了强调搜索空间的利用，参数n1，n2，n3和n4值在每次迭代时都会更新。停止条件设置为最大迭代次数。SCA算法流程如图1所示。

图1 SCA算法优化流程

1.3 评价指标

采用三种常用方法来评价该算法的图像分割性能。分别是Peak Signal-to-Noise Ratio (PSNR)、 Structural Similarity Index (SSIM)和运行时间(CPU time)。

PNSR[17]是通过均方根误差(RMSE)计算得到的，其计算公式为

(6)

均方根误差(RMSE)计算公式为

(7)

式中:Org----原始图像;

Seg----尺寸为M×Q的分割后图像。

SSIM(Org，Seg)=

(8)

式中:μOrg、μSeg----两幅图像的平均强度；

σOrg、σSeg----两幅图像的标准差；

σOrg，Seg----原始图像和分割图像的协方差；

c1、c2----常数。

1.4 基准图像与开发环境

文中在6幅常用灰度图像上对SCA优化后的多阈值分割算法进行了测试，测试图像包括莉娜、猎人、狒狒、桥梁、轮船和辣椒。为了观察该算法的有效性，实验中还使用了一幅单独测试图像(莉娜)。这些测试图像是从USC-SIPI数据库中收集的，该数据库是南加利福尼亚大学公布的经典图像处理数据集。该图库包含很多彩色、灰度图像，是一个经典的图库。USC-SIPI数据库经典图像如图2所示。

图2 用于测试的USC-SIPI数据库经典图像

算法在一台Intel Xeon(R) Gold 6148 CPU 2块、256 GB RAM和NVIDIA Quadro P6000 GPU的PC上使用Matlab 2017a版本进行编译和测试。

2 结果与分析

2.1 不同图像的分割结果比较

在不同图像中设定相同等级的阈值数量来测试经过SCA算法优化后的多阈值分割效果。三种不同阈值数量下各图像分割结果的评价指标参数见表1。

不同阈值数量下，测试图像分割效果如图3所示。

2.2 单张图像测试结果分析

为了更丰富地展示SCA算法优化后的多阈值图像分割结果，研究以莉娜图像为例，结合图像的灰度直方图展示不同阈值数量下的图像分割效果。

展示多个阈值设定情况下的图像分割结果如图4所示。

表1 三个不同阈值数量下各测试图像分割结果的评价指标参数

(a) 阈值数量设定为4情况下测试图像

(b) 阈值数量设定为5情况下测试图像

(c) 阈值数量设定为6情况下测试图像

(a1) 阈值数量=2(a2) 阈值数量=4(a3) 阈值数量=8(a4) 阈值数量=16(a5) 阈值数量=32

(b1) 阈值数量=2(b2) 阈值数量=4(b3) 阈值数量=8(b4) 阈值数量=16(b5) 阈值数量=32

(c1) 阈值数量=2(c2) 阈值数量=4(c3) 阈值数量=8(c4) 阈值数量=16(c5) 阈值数量=32

除此之外，研究统计了使用莉娜图像设定不同阈值后输出的最佳阈值数值，以及其对应的类间方差值，见表2。

表2 莉娜图像在不同阈值设定下输出的最佳阈值及其对应的类间方差

3 结 语

3.1 讨论

从图3可以看出，SCA提供的解决方案在相同阈值设定情况下，对不同复杂程度图像的分割结果存在显著差异。猎人图像在4～6的阈值设定情况下，分割结果要优于其他5组图像。想要从不同复杂程度的图像中获得优秀的分割结果，仍需要尝试不同的阈值设定。从图4可以看出，SCA提供的解决方案并不是设定的阈值数量越多效果越好。在阈值数量分别为2，4，8，16，32的5组测试中，阈值数量小于16时，图像的分割效果逐步提升。在阈值数量设定为32后，分割结果明显虚化，因为当阈值设定为32时，得到的最佳阈值非常接近。这种情况会损害分割，因为只有很少的强度值被认为会生成小的类。从这些结果可以得出，SCA算法在某些情况下无法在大量维度中找到最优方案。

3.2 结论

介绍了一种使用正弦和余弦函数来修改候选解位置的优化算法在多级阈值图像问题中的实现。文中在目标函数Otsu上对SCA进行了测试，以找出图像分割的最佳阈值。与其他类似方法不同，本研究还考虑图像的空间上下文信息来选择阈值。这种方法类似图像的能量曲线，它具有与直方图相似的特性，但也包含了每个像素的邻域信息。

提出的基于SCA的阈值分割方法已经在一组基准图像上进行了测试。此外，考虑到SCA是比较新颖的方法，在结果部分设计两组实验进行了比较。基于统计分析、收敛行为分析和性能指数分析的实验结果表明，SCA算法可以完全胜任研究中提到的多级阈值图像分割任务。证明该算法在本研究问题中的有效性、准确性和鲁棒性。