城市管道清淤机器人数学建模与MATLAB仿真
嵇鹏程,嵇鑫宇
(1.常州市河道湖泊管理处,江苏 常州213022;2.中国矿业大学,江苏 徐州221116)
我国地下排水管道的清淤工作仍普遍采用人工作业的落后方式[1],这种清淤作业方式整体效率低[2]。近年来,水下机器人技术的快速发展为水下机器人在各行各业中的应用提供了条件,本文研制的城市排水管道清淤机器人,采用PID控制技术,使得机器人具有实用性、可靠性、智能性和可操行,可完全代替人工下井作业,使工人完全脱离了恶劣的作业环境。
1 机器人机构系统建模
本文研究的机器人机构由机器人本体、管径适应机构、行走机构、绞刀机构等组成[3],见图1。
1.1 管径适应机构系统的数学建模
以管径适应机构后面的摇杆与机架的铰链点A为坐标系原点,建立如图2所示的坐标系XOY。

图1 管道清淤机器人结构模型
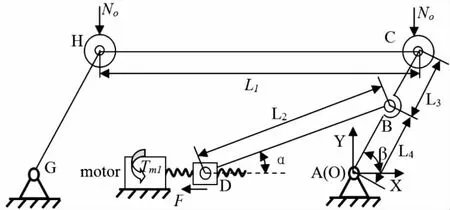
图2 铰链四杆力封闭机构调节方式示意图
图中:Νo为管道内壁作用在适径机构顶轮上的压力,F是螺母受到的水平拉力,Tm1是适径机构驱动电机轴上的输出扭矩。
通过对铰链四杆机构几何尺寸关系式求导和做功守恒原理得出螺母的轴向力F:
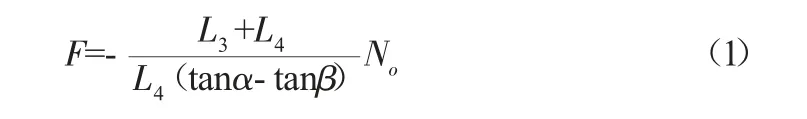
通过对滚珠丝杠移动距离求导和做功守恒原理得出滚珠丝杠扭矩与机器人对管壁压力关系:
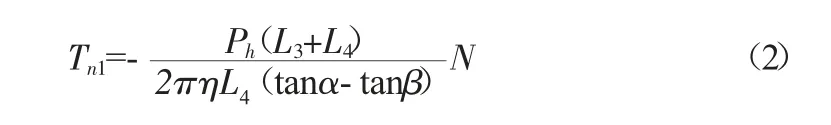
机器人输出的牵引力F牵按600 N计算,驱动轮和管道内壁之间的摩擦系数μ取0.5,则管道内壁作用在车轮上的压力N=1200 N。所以选取滚珠丝杠公称直径为20 mm,选用的型号为FC1B20×4-5-E2,其额定负载是5393 N,摩擦角为φ=10′;螺旋升角γ=3°25′,则其传动效率:
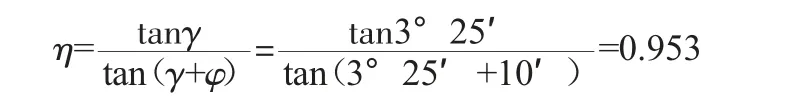
当机器人行走在φ400 mm的管道中时,α=28.7°、β=10.6°,代入式(1)得出F=4895 N;当机器人行走在φ500 mm的管道中时,α=64.2°、β=32.7°,代入式(1)得出F=1121.5 N。
把已知数据代入式(2)可求出滚珠丝杠的扭矩Tn1=4.4515 N·m,可见采用铰链四杆力封闭调节方式时,清淤机器人对管壁压力设定为1200 N的情况下,当管径在400 mm~500 mm范围内变化时,滚珠丝杠上所需的最大扭矩为4.4515 N·m,目前大功率的直流伺服电机都能提供,为此,伺服电机可选用型号为CN-400-10,其额定输出扭矩达到4.5 N·m,最高转矩可达40 N·m,满足该系统的要求。
根据管径适应机构的传动过程,建立的模型结构见图3。
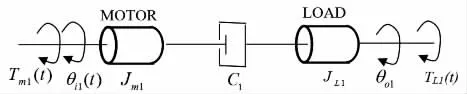
图3 管径适应机构模型结构
图中:C1为电机及滚轴丝杠传动的粘性摩擦系数;TL1(t)为滚珠丝杠上的转矩;θi1(t)为电机轴的转角;θo1(t)为滚珠丝杠的转角;Jm1为电机轴的转动惯量;Tm1(t)为电动机的转矩;JL1为负载的转动惯量。
根据模型结构图求得:
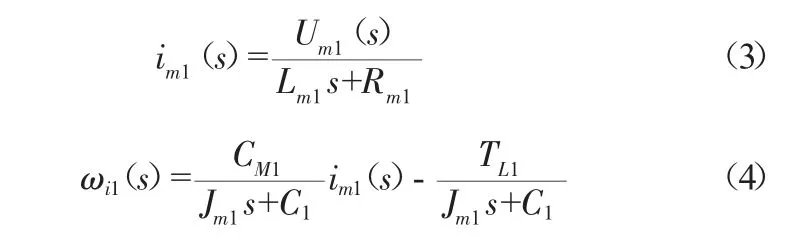
式中:Um1为电动机的电枢电压;CM1为电动机电磁力矩系数;Rm1为电动机的电枢电阻;ωi1为电动机轴的角速度;im1为电动机电枢电流;Lm1为电枢电感。
由式(1)~式(4)得到电机传动模型方框图,见图4。
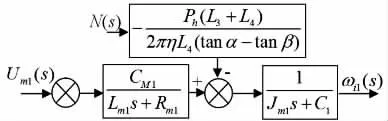
图4 管径适应机构驱动电机传动模型方框图
由图4可求出电机角速度的表达式:

1.2 行走机构系统的数学建模
由于该机器人要求中低速行驶,而电动机具有较高的额定转速,因此,电动机和轮子之间必须装设减速机构,行走机构示意图见图5。
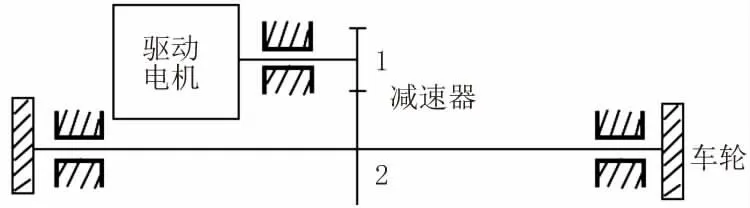
图5 行走机构示意图
1.2.1 齿轮相关参数计算
齿轮传动比i=4,故取Z1=12,Z2=48,m=2,α=20°,则有:
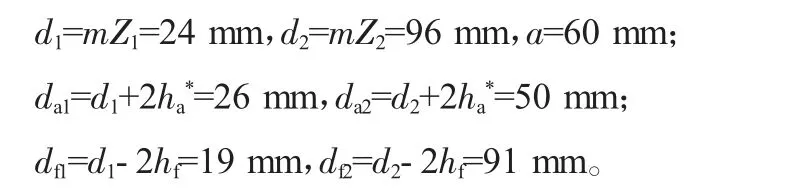
1.2.2 负载转矩的折算
为便于选择电机,先将各转动部分的转矩和转动惯量或直线运动部分的质量都折算到电机轴上。
选定轮子的直径D=120 mm,则轮子的周长C≈0.38 m,清淤机器人的正常行驶速度v机设定为0.1 m/s,当牵引力F牵=600 N时需要电机的功率为PL=F牵v机=60 W,按平均传动效率η为95%,则输入功率PM≈63.15 W,实际我们选的直流电机的额定功率可选择为85 W,如果取机器人正常清淤时电机的最高转速为1000 r/min,则其负载转矩为:
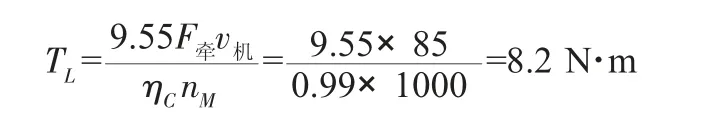
式中:ηC为电动机拖动机械运动时的传动效率,这里ηC取95%;nM为电动机轴的转速。
根据上面计算出的功率和扭矩,选择直流伺服电机的型号为CN-800-10,其额定输出扭矩达到8.3 N·m,最高转矩可达80 N·m,可以满足本设计所需的8.2 N·m。
1.2.3 转动惯量的折算
转动惯量对运动特性有很大的影响,不但与加速能力、加速时驱动力矩及动态的快速反应有关,在闭环或半闭环系统中还影响系统的稳定性,因此,须核算转动惯量。清淤机器人的质量为48 kg,折算到电动机轴上的总转动惯量公式为:

式中:JM、JZ为电动机轴、轮子轴上的转动惯量;j1=ωM/ω1为电动机与轮子轴之间的速比;ωM、ω1为电动机轴、轮子轴上的角速度。
外径为D、内径为d的圆环转动惯量公式为:
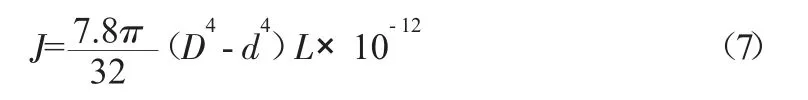
(1)对于电机轴上的齿轮,D1=24 mm,d1=12 mm,宽L1=20 mm,代入式(7)可求出其转动惯量为:
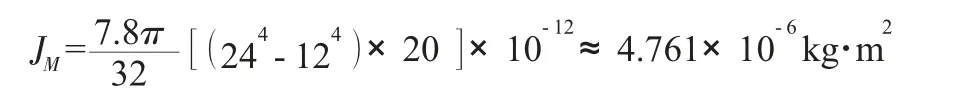
(2)对于轮子轴上的齿轮,D2=96 mm,d2=16 mm,宽L2=20 mm,同样代入式(7)求出其转动惯量为:
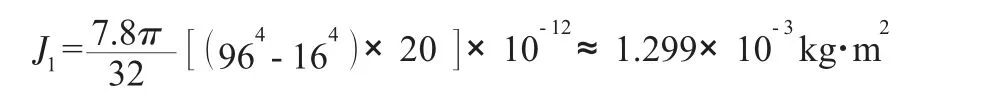
(3)清淤机器人折算到电机轴上,m=48 kg,则:
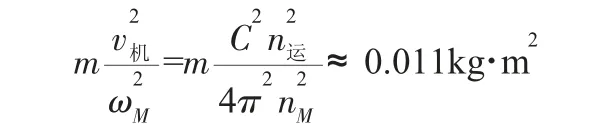
将上述数据代入式(6)中求出J=0.012 kg·m2。
行走机构模型方块图见图6,其中,C2为刚性联轴器的阻尼系数,TL2(t)为负载力矩;Jm2、JL2分别为直流电机轴和车轮轴的转动惯量;θm2(t)和θo2(t)分别为电机轴和车轮轴的转角;i为齿轮传动比;Td(t)为折算到在电动机轴上的负载转矩;Tm2(t)为电机力矩。

图6 行走机构驱动系统模型方框图
根据模型结构图求得:
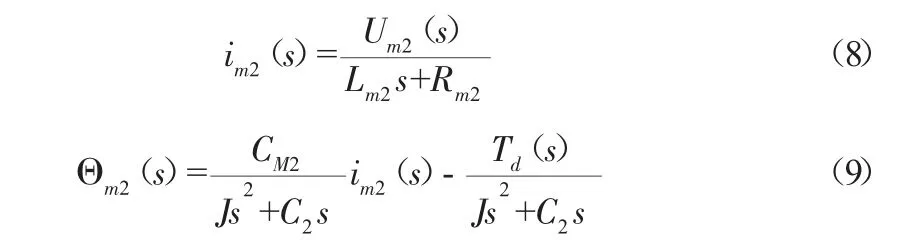
式中:Um2为电枢电压;CM2为电动机电磁力矩系数;im2为电枢电流;Rm2为电枢回路电阻。
又因为电机轴与车轮轴单位时间内的转角之比为:

机器人的牵引力与其它负载力的关系为:
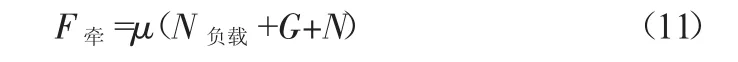
式中:μ为机器人与管道内壁的摩擦系数;N为机器人适径机构对管道内壁的正压力;G为机器人的重量;N负载为机器人拖动负载(电缆线)的拉力。
由式(8)~式(11)得到行走机构系统方框图,见图7。

图7 行走机构系统模型方框图
式中:C为电动机拖动机械运动时的传动效率,取95%;nM为行走机构驱动电机轴的转速;v机为机器人的行走速度。
在建立管道机器人动力传动系统模型后,可得到行走机构轮子输出转角的表达式为:
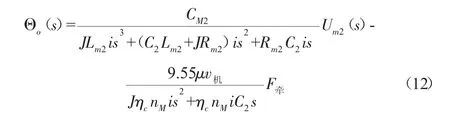
2 机器人机构控制算法与仿真
为了确保城市管道清淤机器人能够平稳、可靠地运动,需要对机构协调运动控制策略进行深入研究[4],城市管道清淤机器人系统的核心是智能控制算法,因此,关键技术就是要选取合适的智能控制算法。
2.1 行走机构闭环控制及仿真
行走机构采用位置-电流二环控制,二环参数调试时遵循从内环到外环的顺序,先调试电流环,最后是位置环,电流环处于内环,调试时首先考虑其快速跟随性,即输出电流能够跟随给定电流的变化;电流环采用PI控制算法,位置环作为外环,直接决定了伺服系统的动态和静态性能,采用PD控制算法。
2.1.1 电流环参数的整定
电流环采用PI控制,其传递函数框见图8。
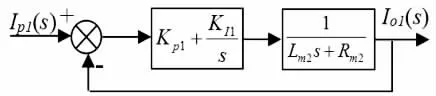
图8 电流环传递函数框图
电流环的传递函数为:
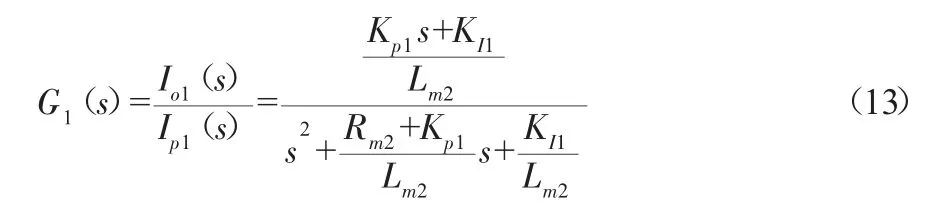
令式(13)参考函数模型为:
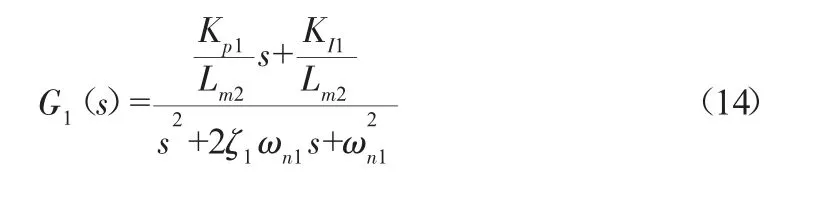

表1 CN-800-10的性能参数
选择电机为CN-800-10,主要性能参数见表1,由于需要较快的响应速度,使Io1(s)≈Ip1(s),根据实际情况这里取ζ1=0.707、ωn1=2500 rad/s代入相关参数可求出:KI1=23125,Kp1=17.72。
2.1.2 位置环参数的整定
位置环采用PD控制,位置环的数学模型可由图9所示传递函数方块图表示,这里已经简化为单位反馈模型,因为位置反馈系数Ks为纯增益。图中Θp(s)=vs/Ks是给定的位置,也是期望的位置值,T1为电机有效转矩。

图9 位置环传递函数框图
传递函数为:
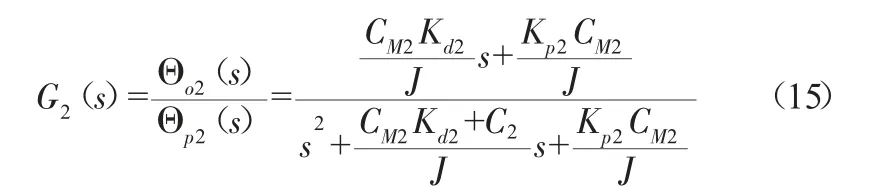
令式(15)的参考模型为:
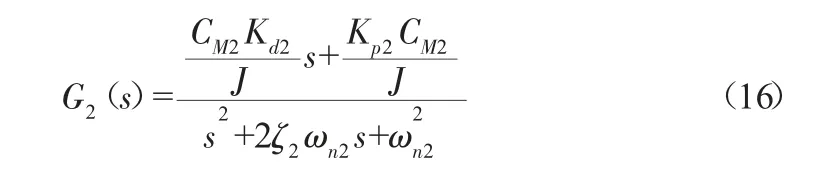
这里取ζ2=0.707、ωn2=125 rad/s,设当机器人行走在直径为400 mm管道中时,α=28.7°、β=10.6°。代入相关参数可求出:Kp2=203.804,Kd2=3。
2.1.3 仿真分析
当输入信号分别为阶跃信号、斜坡信号、正弦信号时,系统的输出响应信号和输入信号对比见图10。
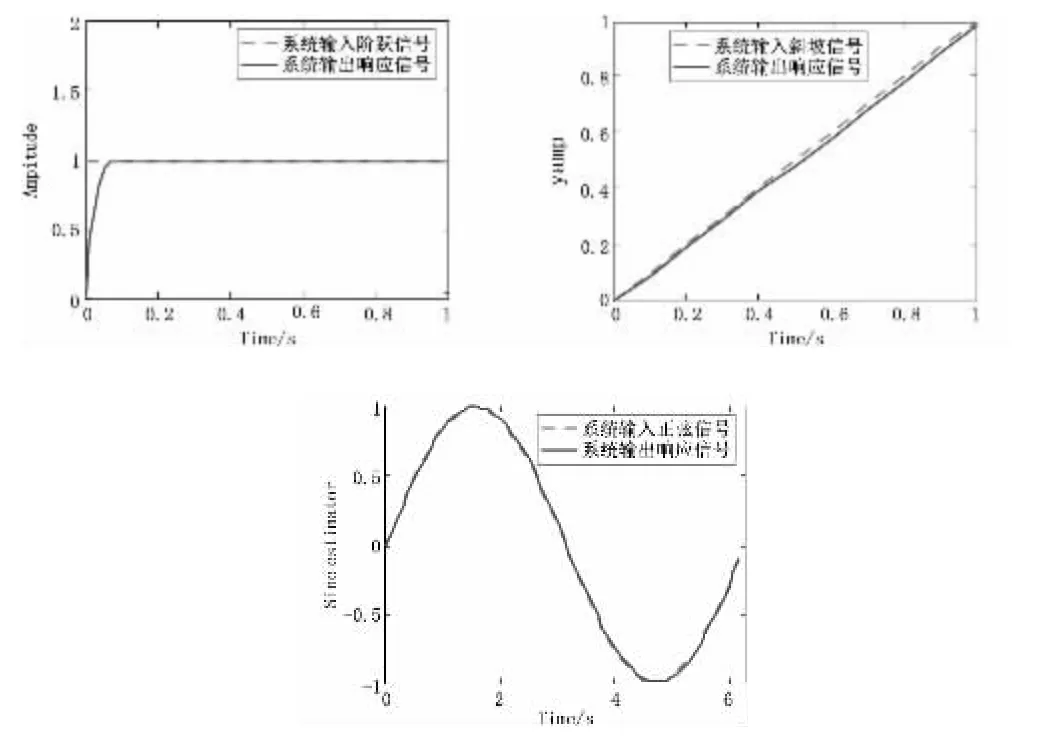
图10 分别输入阶跃信号、斜坡信号、正弦信号与输出响应曲线对比图
从图10可以看出系统在PID参数整定后,具有较小超调量,较短调节时间和较好可控性。
2.2 管径适应机构压力闭环控制及仿真
通过建立管径适应机构动力模型,给出期望牵引力F牵,计算出来对管壁的期望压力值N,通过比较实时反馈来由压力传感器测试的实际压力值No与输入的压力期望值N得出的差值ΔN,PID控制器调整适径驱动电机保持实际拉力No趋向到N。压力传感器的反馈系数KV=200,电压放大倍数KU=5。PID控制的传递函数框图见图11。

图11 管径适应机构闭环系统PID控制传递函数框图
2.2.1 电流环参数的整定
为了得到较快的响应时间,电流环仍采用PI控制,使Io2(s)≈Ip2(s),对PI参数进行设计时,仍按经验值求取,得到电流环传递函数为:
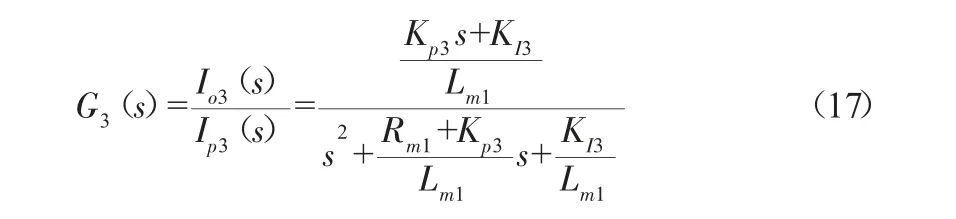
令式(17)的参考模型为:
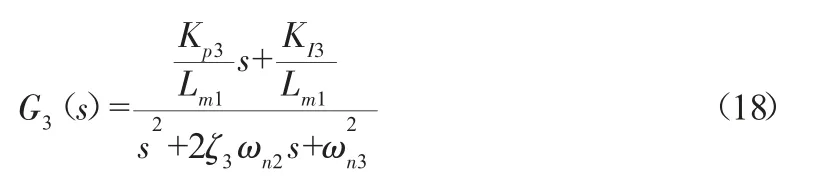
选择的电机为CN-400-10,主要参数见表2。
根据管径适应机构的实际工作情况,这里取ζ3=0.707、ωn3=2500 rad/s代入相关参数可求出:Kp3=40081.5,KI3=21.1。
2.2.2 压力环参数的整定
压力环作为外环,决定伺服系统的动态和静态性能,所以
采用PD控制技术。
由图11可得到输出角与压力的传递函数为:
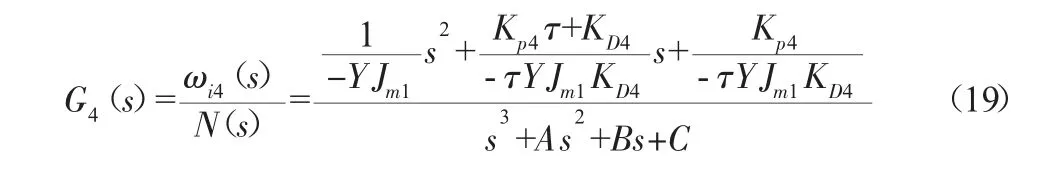


表2 CN-400-10的性能参数
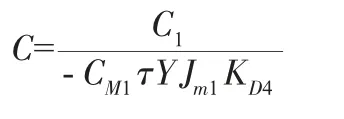
令式(19)的参考模型为:
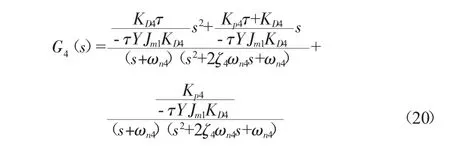
这里取ζ4=0.707、ωn4=12.5 rad/s代入相关参数解得τ=0.5,KD4=12,KP4=8。
所以系统的传递函数为:
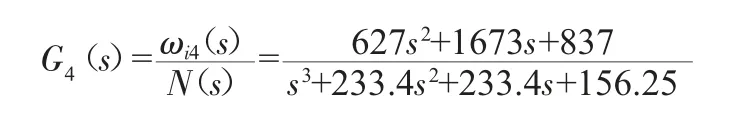
2.2.3 仿真分析
绘出管径适应机构闭环系统的阶跃响应曲线和Bode图,见图12和图13。
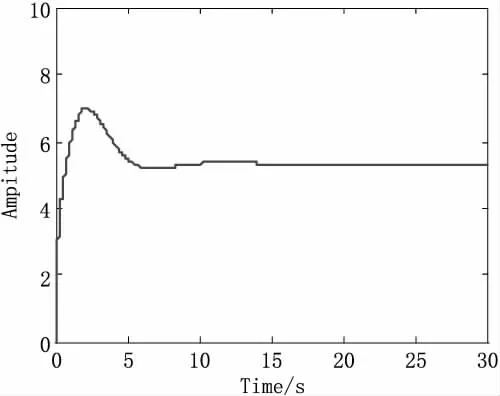
图12 PID控制的闭环系统阶跃响应曲线
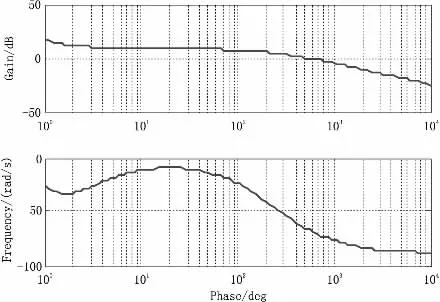
图13 PID控制的闭环系统Bode图
从图12~图13可以看出系统的响应是稳定的,超调量较小,过渡过程时间为6 s左右。
3 结语
本文通过对机器人行走机构、管道适径机构进行数学建模和计算来选取主要部件,并根据机器人的各机构运行特点选取相应的控制策略,并通过MATLAB软件进行仿真表明,该系统运行稳定,可替代性强,能够满足城市排水管道清淤工程的需要。

