复合梯形明渠均匀流正常水深的显式迭代求解

傅铭焕，陈炳斌

（1.浙江省水利水电勘测设计院，浙江 杭州310002；2.绍兴烈辰建设有限公司，浙江 绍兴312030）

0 引言

均匀流正常水深的计算是渠道水力学的一个常见问题，梯形断面作为农业工程和水利工程的典型断面，其正常水深的求解备受关注。

由于断面形式的特殊性，梯形断面明渠的均匀流正常水深求解往往需要多次迭代计算［1］。随着研究的深入，文献［2-10］提出了梯形明渠正常水深新的迭代计算式，大大减少了正常水深计算的工作量。

近年来随着科技的进步与工艺的提升，各种人工渠道（复合梯形明渠）应运而生。相较于一般的梯形明渠或天然河道，复合梯形明渠往往具有不同的边坡系数或多种材质壁面（含渠底及两岸护坡）。故其正常水深的求解相较于一般梯形明渠愈加复杂。

对于复合明渠，现阶段缺少对其正常水深计算的研究。根据别洛康和爱因斯坦的复合糙率系数公式，研究复合梯形明渠均匀流正常水深的计算方法，提出其稳定的显式迭代求解公式。

1 综合糙率系数公式的选取

图1为一复合梯形明渠示意图。图中Q为过渠流量；i为渠道坡降；nc为复合梯形明渠综合糙率系数；h0为梯形明渠均匀流正常水深；b为复合梯形明渠底宽；m1、m2分别为梯形两侧边坡系数；n1、n2、n3分别为梯形两侧边坡及渠底的糙率系数；A1、A2、A3分别为梯形两侧边坡及底部对应的过水面积；χ1、χ2、χ3分别为梯形两侧边坡和渠底的湿周。

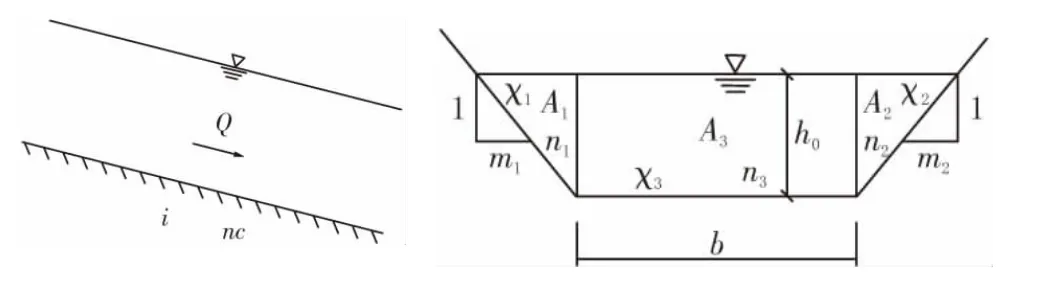
图1 复合梯形明渠简图

渠道均匀流正常水深的求解主要根据明渠恒定流连续性方程和谢才公式而得［11］。其中，谢才公式须知道复合梯形明渠的综合糙率系数nc。现阶段，nc的常用计算公式有巴甫洛夫斯基公式、别洛康和爱因斯坦公式和加权平均法公式，分别如下［1］。

巴甫洛夫斯基公式：

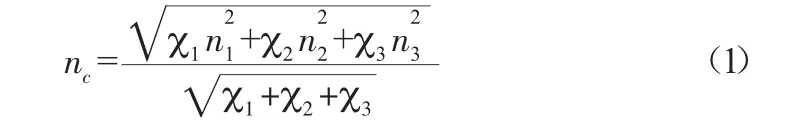
别洛康和爱因斯坦公式：

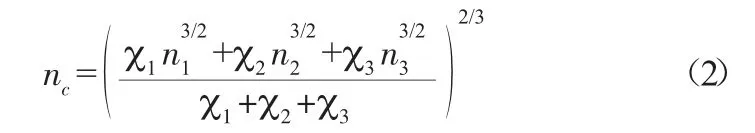
加权平均法公式：

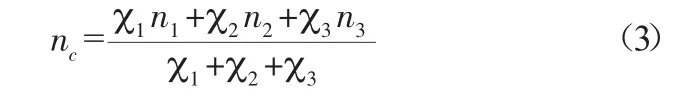
本文借用张红岐［12］的试验资料，对式（1）～式（3）计算的精度进行验证，详细试验参数及计算结果见表1。由表1可知，别洛康和爱因斯坦公式计算的综合糙率系数位于3个公式计算值的中间。巴甫洛夫斯基公式计算的平均误差为2.77%，最大误差为7.77%；别洛康和爱因斯坦公式计算的平均误差为2.74%，最大误差为7.08%；加权平均法公式计算的平均误差为2.74%，最大误差为6.35%。3个公式计算的20组试验工况精度基本相同，均能满足工程运用。对于个别试验工况计算偏差相对较大，分析认为是由于实际施测的测量误差引起的。因为渠道实际糙率系数并无直接计算公式，而需根据实际测量的流速、底坡及断面参数反算而得。文献［13］的研究也表明，原型观测糙率系数测定的最大误差分别为5.0373%和4.3050%。由上述分析可以看出，式（1）～式（3）均能作为计算复合梯形明渠均匀流正常水深的综合糙率计算公式。

巴甫洛夫斯基公式假定各湿周的过水断面平均流速相等以及各过水断面的水力半径相等。别洛康和爱因斯坦公式仅假定了各湿周的过水断面平均流速相等，而未做其他假定。出于公式的理论性，加之式（2）计算值位于式（1）和式（3）的中间，本文选取别洛康和爱因斯坦公式（式（2））作为复合梯形明渠的综合糙率系数计算公式。

2 正常水深迭代公式的推求

根据连续性方程及谢才公式，可得复合梯形明渠均匀流流量公式为：

式中：Ac=A1+A2+A3为复合梯形明渠总的过水断面面积；χc=χ1+χ2+χ3为复合梯形明渠过水断面总湿周。

将式（2）带入式（4），整理得：

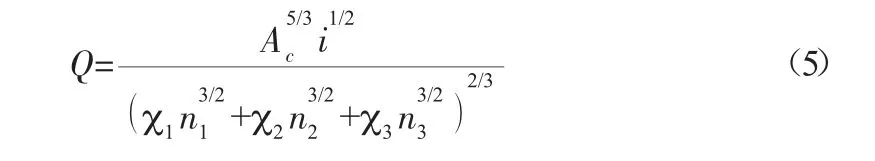
由图1可得复合梯形明渠总的过水断面面积：

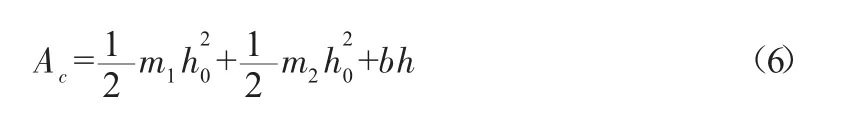
复合明渠各段湿周分别为：

将式（6）和式（7）带入式（5）并整理得：

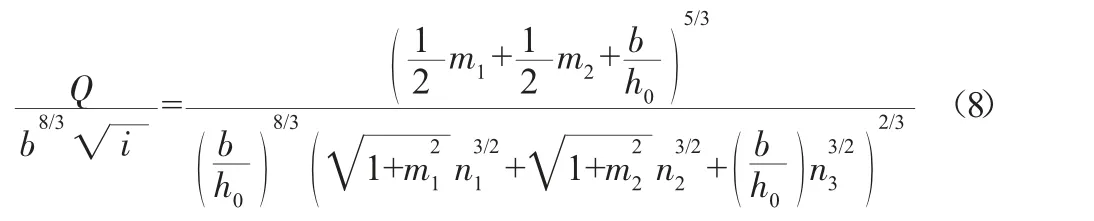
由式（8）可知，复合梯形明渠均匀流正常水深的计算是一个复杂的隐函数求解过程。令宽深比β=b/h0，并带入式（8）得：

式（9）可变形为：

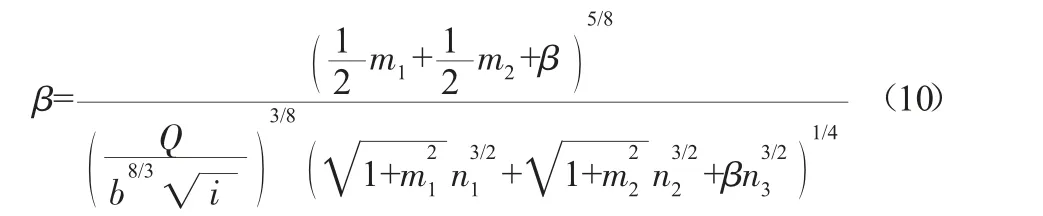
由式（10）可得复合梯形明渠宽深比的迭代计算式，即：

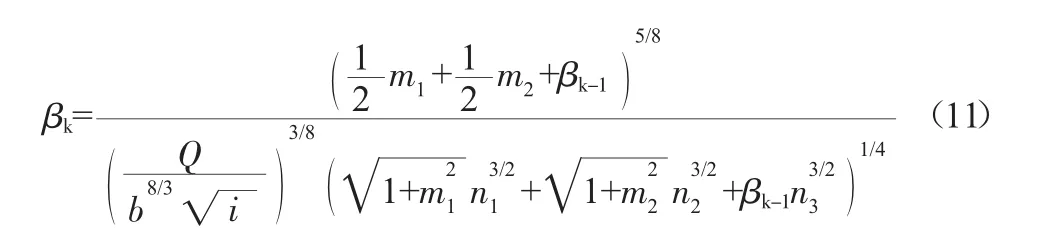
应用式（11）进行迭代求解，须先证明式（10）的导函数在宽深比β∈（0，+∞）的变化范围内收敛。令β=f（β），并对式（10）求导可得：

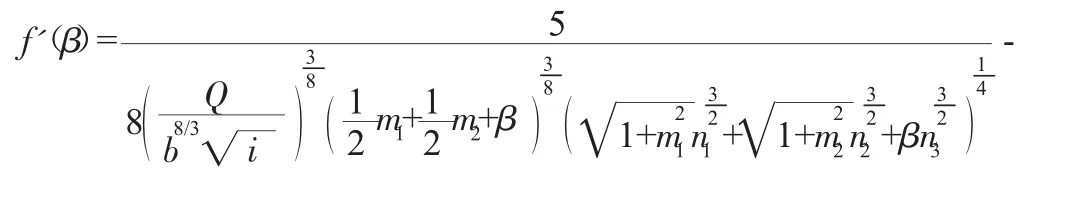
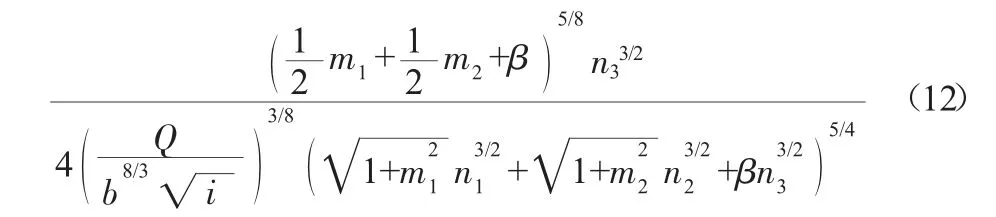
对式（10）进行转换变形，得：

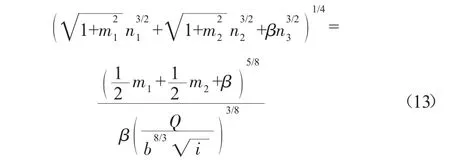
将式（13）带入式（12）可得：

将式（2）和式（7）带入式（14），可得：

前文已述别洛康和爱因斯坦公式假定了各湿周的过水断面平均流速相等，即：

式中：vc为复合梯形明渠全断面平均流速；v1、v2、v3分别为A1、A2、A3过水断面的平均流速。

由式（16）可知：

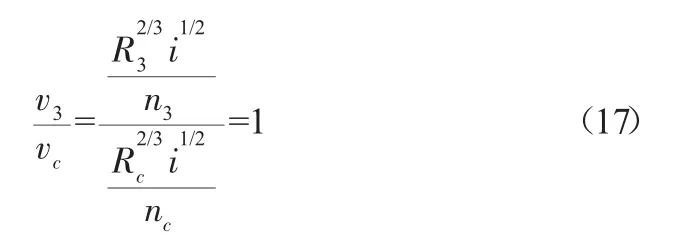
式中：Rc=Ac/χc为过水断面的水力半径；R3=h0为A3过水断面的水力半径。

由式（17）可得：

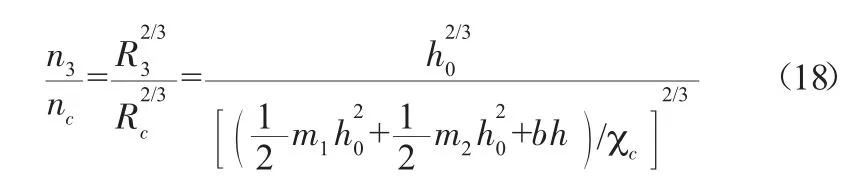
将公式（18）带入公式（15）可得：

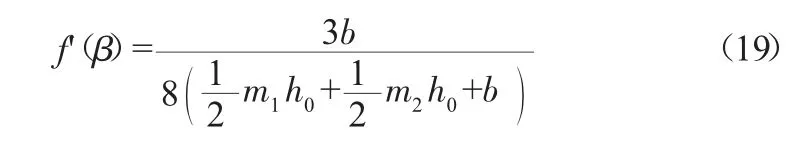
令B=（m1h0+m2h0+b）为复合梯形水面宽度，则由图1可知，复合梯形上下底面的平均宽度故式（19）可简化为：

对于宽深比的初值，本文根据其变化范围的上下限来定义。当宽深比趋近于0时，由式（11）可得：

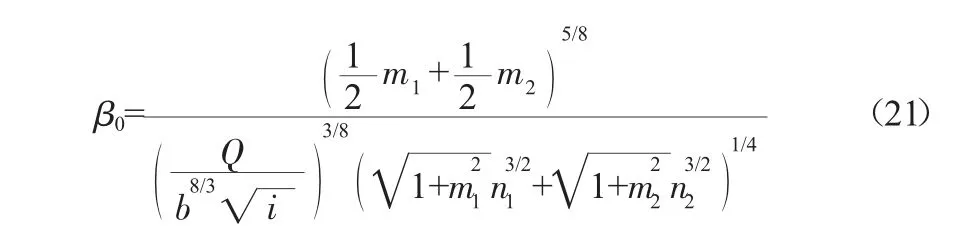
当宽深比β趋近于正无穷时，β0也趋近于正无穷，其初值无法确定。故本文取式（21）的计算值作β0为式（11）的迭代初值。

将β=b/h0分别带入式（11）和式（21），可得复合梯形明渠均匀流正常水深的显示迭代计算式：

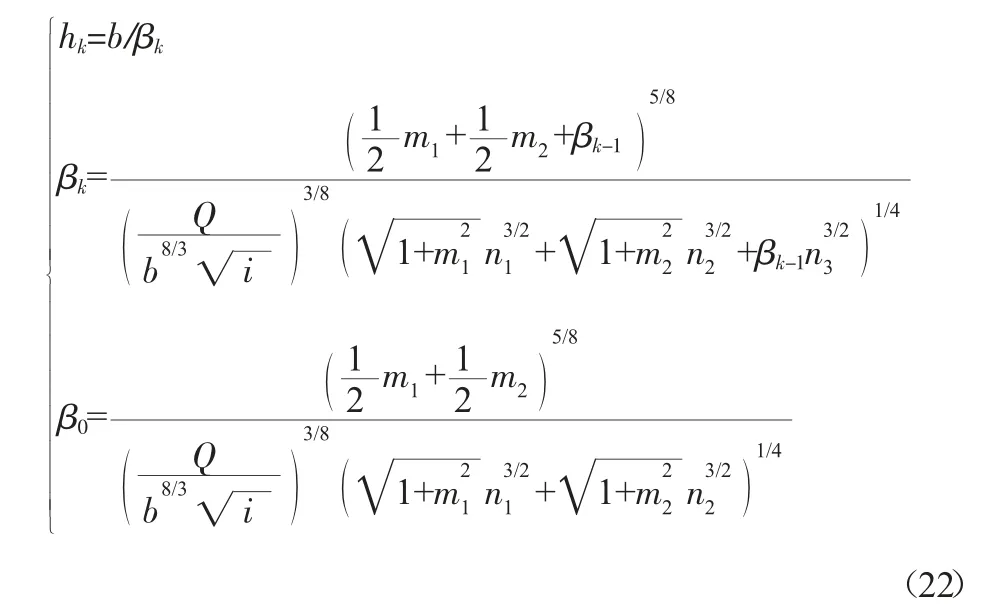
式中：hk为迭代的正常水深值。

3 算例与验证

由于式（8）的正常水深计算式是依据式（2）而来，故以文献［12］中的20组试验工况为例，用式（8）多次迭代计算的复合梯形明渠均匀流正常水深，验证用式（2）计算复合梯形糙率的可行性，具体计算结果见表1。由表1可知，式（8）多次迭代计算的正常水深平均误差为1.42%，最大误差为3.8%，能满足工程运用要求。可见，用式（2）计算的综合糙率系数来求解复合梯形明渠正常水深是可行的。

本文同时用文献［12］中的20组试验工况，分析式（22）的迭代计算效果，具体见表2。由表2中20组试验工况可知，本文式（22）迭代计算的宽深比在进行5次迭代后，其值已经无限接近于式（8）计算的多次迭代值。由此可知，式（22）迭代公式是正确的。式（22）进行3次迭代后，20组工况的最大误差为-2.35%，但进行第4次迭代后，所有工况误差均小于1%。可见，本文式（22）具有较快的收敛特性，只需迭代3～4次，其计算精度就足以满足设计要求。同时，式（22）迭代的宽深比比多次迭代值略小，故其计算的正常水深值比多次迭代值略大，工程运用偏于安全。

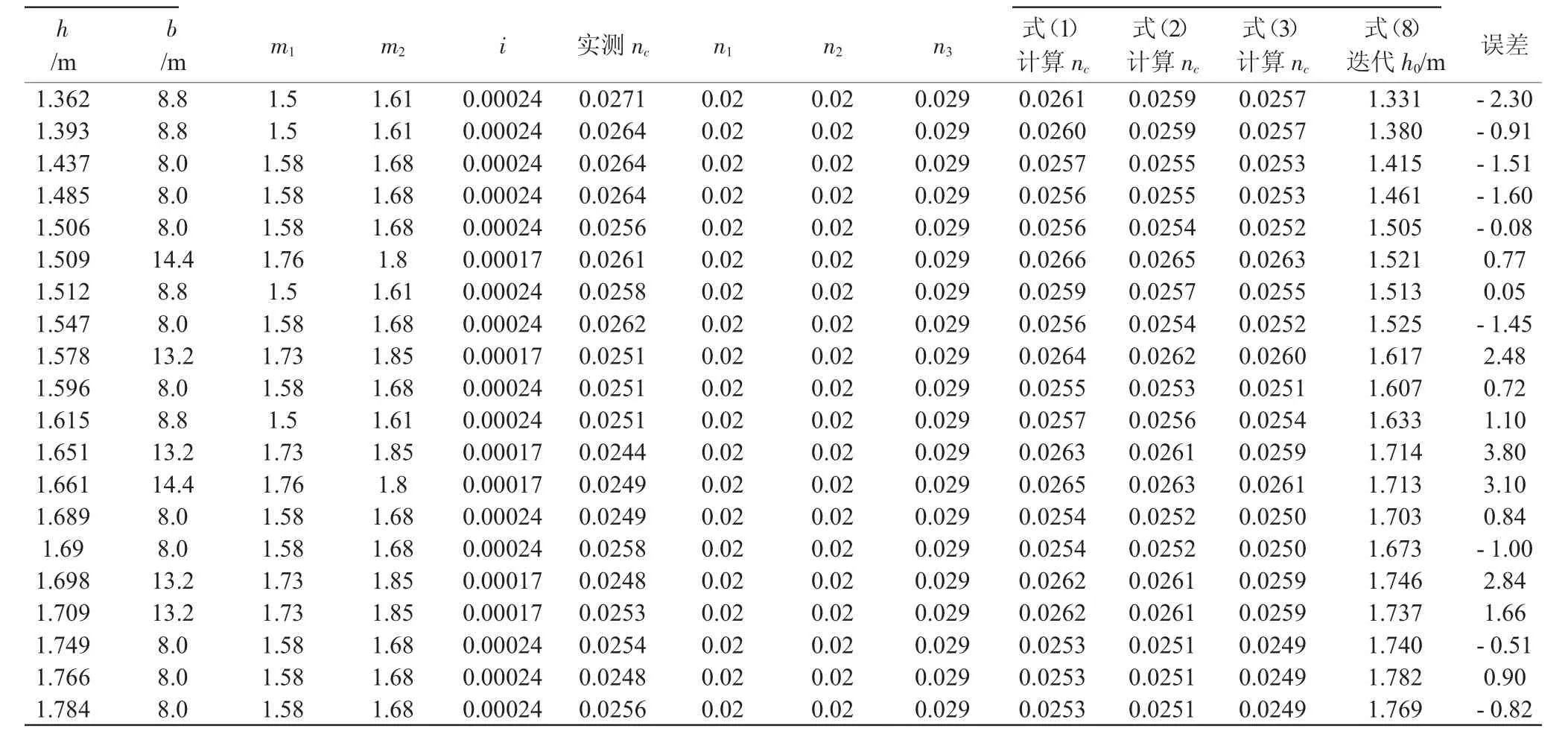
表1 nc与h0的验证

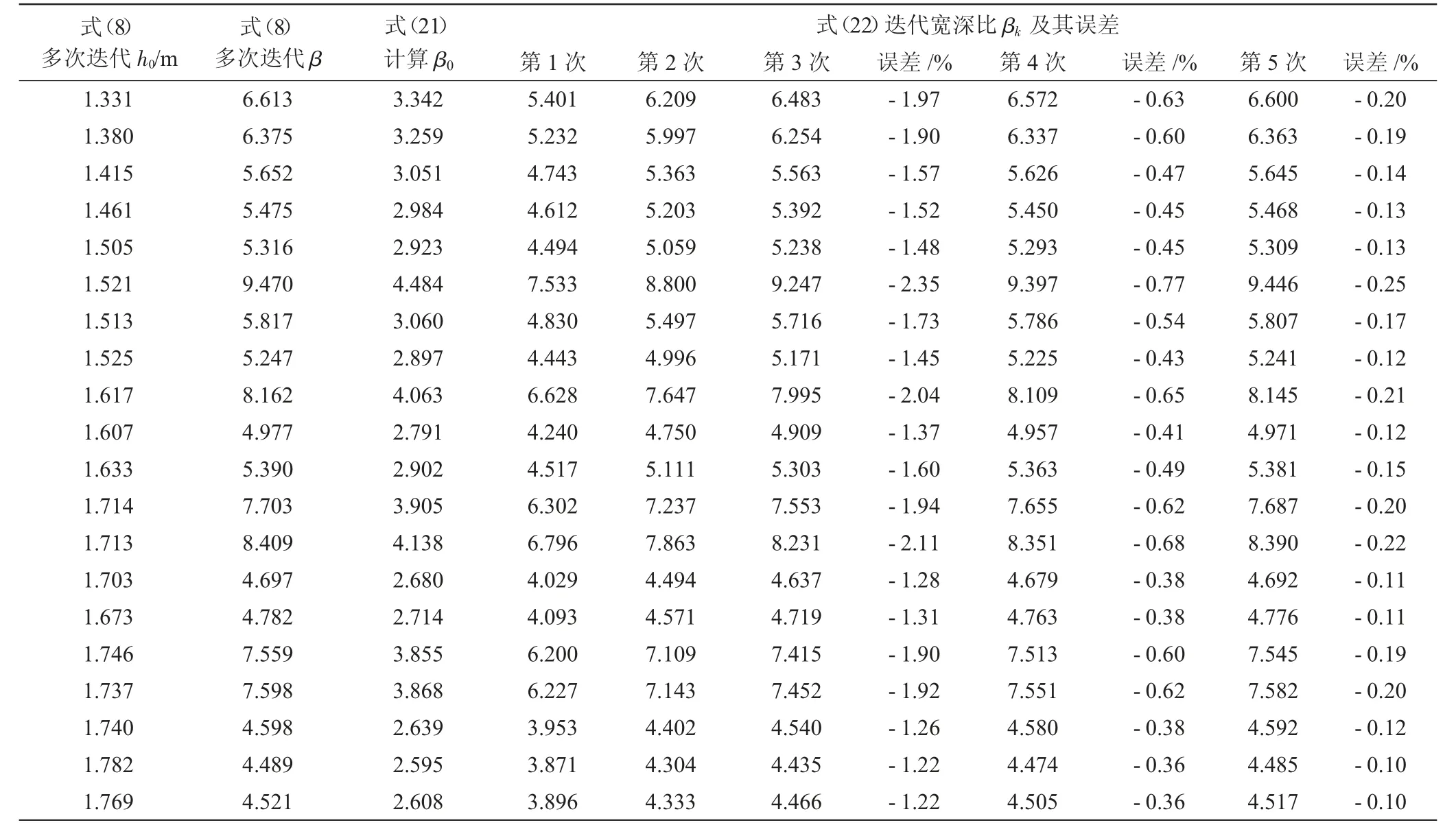
表2 βk的迭代计算

4 结语

本文根据文献［12］的试验工况，对现有常用的复合梯形明渠糙率公式——式（1）～式（3）进行分析与比较。结果表明，式（1）～式（3）计算精度基本相同，其中式（2）的计算值位于式（1）和式（3）的中间。根据别洛康和爱因斯坦的复合明渠综合糙率计算公式，推求了均匀流正常水深的显性迭代计算式。结果表明，用别洛康和爱因斯坦公式计算复合梯形明渠正常水深是可行的。式（22）迭代求解的复合梯形明渠正常水深只需3～4次迭代计算，就能满足工程运用要求。式（22）经4次迭代求解后，正常水深的平均误差均小于1%。