水陆两栖球形机器人辅助鳍的水动力特性
迟兴,战强
(北京航空航天大学机械工程及自动化学院,北京,100191)
球形机器人将驱动机构、控制电路和感知系统等重要部件封闭在球形外壳的内部,对其形成密闭保护。该结构特点使得球形机器人容易适应复杂严苛的外部环境,在环境探测、安保防爆、军事侦察等领域具有广阔应用前景[1]。传统的球形机器人应用局限于陆地环境,通过配备额外的驱动能力可以拓展球形机器人的应用环境到水域,使其具有水陆两栖特性,增强其环境适应性。为此,需要解决传统球形机器人在水域中运动时驱动能力不足这一关键问题。
一些研究者通过给传统球形机器人配备适合于水中运动的驱动装置,研制了不同类型的水陆两栖球形机器人。GUO 等[2-4]介绍了一种由复合驱动系统提供动力的水陆两栖球形机器人,该复合驱动系统由4个相同的驱动单元组成,每个驱动单元使用1 个喷水推进器和2 个垂直布置的伺服电机,有四足步行模式和喷水推进模式2 种运动模式,分别用于机器人的陆地运动和水中运动。KAZNOV 等[5]研发了水陆两栖球形机器人GroundBot,该机器人利用重心偏移原理实现陆地运动和水面运动,球形外壳上设计了点状凸起带,以提高机器人的水面移动速度。李艳生等[6-7]设计了一种利用螺旋桨推进的水陆两栖球形机器人,机器人中心位置处安装了1个内部包含推进螺旋桨的柱形涵道,该机器人在陆地上利用重心偏移实现滚动运动,在水中时则利用螺旋桨推进的方式运动。
通过在球壳两极地带黏附辅助鳍,提高水面运动推进力,可实现利用1套驱动装置完成球形机器人两栖运动的目标。已有一些研究参考机翼理论对辅助鳍进行了力学特性分析[8]。HEALEY 等[9]给出了AUV 叶片整周旋转中的升力和阻力计算公式,GEORGIADES 等[10]通过实验探究了叶片受力和往复运动振幅和周期的关系,BEHBAHANI等[11-12]研究了仿生鱼胸鳍划水动作时的水动力特性,READ 等[13-14]给出了叶片俯仰和升沉运动的推进力,刘鹏等[15-16]分析了运动参数对水翼推进性能的影响。YANG等[17-18]利用CFD方法给出了水轮机叶片之间的速度分布和压力分布,张万超等[19-20]分析了叶轮受浪流扰动产生横摇运动时的水动力性能。在常规的叶片水动力分析中,叶片通常整体浸入液体中,其湿面积保持不变,压力中心也不变。
本文提出利用辅助鳍改善球形机器人水面运动性能的设计方案,通过在球壳上黏附辅助鳍,设计一种紧凑高效的水陆两栖球形机器人。分析特殊平面形状的单片辅助鳍在运动周期中入水面积和形心的变化规律,基于机翼理论推导液体作用在辅助鳍上的升力和阻力计算公式,给出水平分力和竖直分力表达式。利用傅里叶级数对水平分力和竖直分力进行拟合,针对球壳上不同数量辅助鳍配置方式,给出傅里叶级数表示的水平分力合力和竖直分力合力计算公式。
1 水陆两栖球形机器人系统简介
附加辅助鳍的水陆两栖球形机器人由内部驱动单元和球壳2部分组成,内部驱动单元包括机器人的动力系统和控制电路,球壳由左、右两半球壳组成,作为运动执行部件,同时对内部驱动单元形成密闭保护,如图1所示。

图1 水陆两栖球形机器人Fig.1 Amphibious spherical robot
黏附在球壳外表面两极地带的辅助鳍数量可灵活配置,一种典型的配置方式是在左右两半球壳上各安装8片辅助鳍,且位于半球壳上的辅助鳍关于中心轴呈放射性分布,其示意图如图2所示。图中O-XYZ为固定在球壳上的随体坐标系,Y轴与中心轴重合,R为球壳半径;1~8代表8个辅助鳍,相邻辅助鳍之间的相位差为45°。辅助鳍ABC区域的横截面形状近似为钝角三角形,在球壳表面的安装位置由ζ1和ζ2确定,ζ1,ζ2和顶角ζt共同决定了辅助鳍的平面形状。

图2 辅助鳍安装示意图Fig.2 Installation diagram of assistant fins
当机器人执行陆地运动时,位于底部的辅助鳍高于地面,即使机器人产生沿X轴方向的滚转扰动,辅助鳍也不易与地面发生碰撞;当机器人执行水面运动时,位于底部的辅助鳍部分浸没到液体中,液体会在辅助鳍上产生额外的推进力。
2 单片辅助鳍力学特性
2.1 单片辅助鳍升力和阻力
辅助鳍受力分析如图3所示,在辅助鳍上建立惯性坐标系P-XYZ,其中原点P为辅助鳍的压力中心,坐标轴Z垂直纸面向外,倾角φ为辅助鳍平面从X轴正向逆时针转过的角度。液体作用在辅助鳍上的力可以分解为升力L和阻力D,升力方向垂直于来流方向,阻力方向与来流方向一致。

图3 辅助鳍受力分析Fig.3 Force analysis of a fin
考虑机器人在静止液体表面的运动,当球壳绕中心轴旋转时,机器人整体沿X轴负向以速度Vs移动。辅助鳍随球壳一起平移和旋转,其相对液体的速度Vf是牵连速度Vs和相对速度Vn的矢量和,即

相对速度Vn方向垂直于辅助鳍平面,幅值为|Vn|=ωslPY。ωs为球壳相对中心轴的旋转角速度,lPY为压力中心P到中心轴间的距离。
运用运动转换原理,即认为机器人是固定的,观察液体相对机器人的运动,可以认为液体以一定速度冲击到辅助鳍上,从而对辅助鳍施加力的作用。相对辅助鳍的来流速度为Vw,Vw与Vf幅值相等而方向相反,即

记速度矢量Vs和-Vn之间的夹角为β,β∈[0,π/2],则β与倾角φ之间的关系如下:

来流速度Vw的幅值为

Vw和Vn之间的夹角γ的取值范围为[0,π/2],γ可通过下式计算:

攻角αe为来流速度Vw与辅助鳍平面之间的夹角,攻角αe和γ之间的关系如下:

当液体以速度Vw冲击到辅助鳍上时,液体对辅助鳍施加的合力作用于压力中心,合力可以分解为升力L和阻力D[10]:

式中:ρwater为水的密度,S为浸入水中的辅助鳍平面的面积;CLmax为最大升力系数,CDmax为最大阻力系数。由式(7)和(8)可知,升力和阻力与来流速度幅值|Vw|和面积S正相关。在辅助鳍随球壳运动的过程中,|Vw|和S均为辅助鳍倾角φ的函数,这使得升力和阻力的计算变得复杂。
将作用于辅助鳍上的升力和阻力在惯性坐标系P-XYZ中分解为
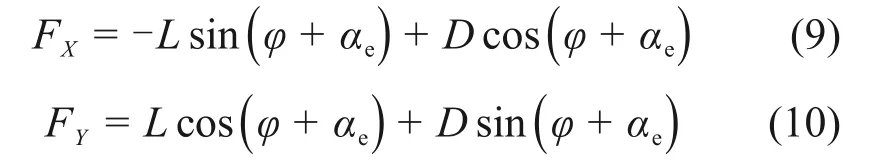
式中:FX和FY分别为液体对单片辅助鳍的作用力在水平方向和竖直方向的分量。水平分力FX的方向与机器人运动方向相同,表现为机器人的推进力。竖直分力FY对机器人运动影响较小,仅进行简单讨论。
2.2 工作周期中的关键角度
辅助鳍ABC工作周期中临界状态如图4所示。
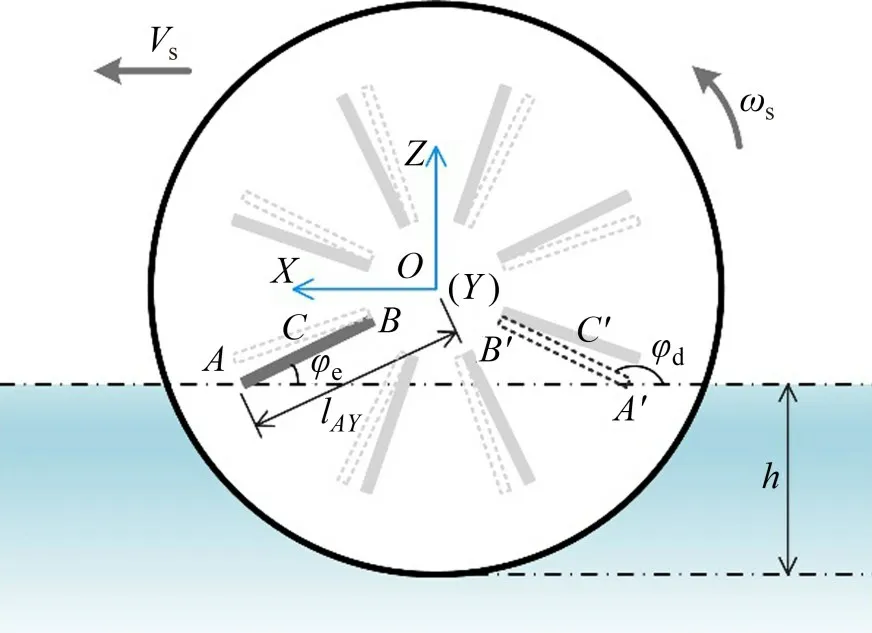
图4 辅助鳍工作周期中的临界状态Fig.4 Critical states in a work cycle of fin
辅助鳍前缘A和中心轴之间的距离为lAY,lAY=Rsinζ2;浸入液面下的球壳高度为h。当前缘A刚好和液面接触,即将开始浸入液体的临界状态,倾角φe为

在辅助鳍逆时针转过一定角度,前缘A即将离开液面的临界状态,倾角φd为

当辅助鳍顶点C刚好位于液面上时,倾角φc为

在机器人水面运动过程中,当某辅助鳍倾角φe≤φ≤φd时,该辅助鳍部分浸没到液体中,液体能够对其施加力的作用;否则,该辅助鳍位于液面上方,液体对其无力的作用。
2.3 辅助鳍入水面积和形心
辅助鳍的升力和阻力与其浸入液体中部分的面积和形心有关。以前缘A点为原点,建立局部坐标系A-uv,其中uv平面与辅助鳍平面平行,u轴与中心轴平行,如图5所示。

图5 辅助鳍入水面积示意图Fig.5 Wetted surface area of a fin
原点A在随体坐标系O-XYZ中的坐标为(Rsinζ2cosφ,Rcosζ2,Rsinζ2sinφ)。在局部坐标系A-uv中,直线AC和BC的方程分别为

圆弧的方程为

当φe≤φ≤φd时,浸入液体中的辅助鳍长度lim为

由于辅助鳍平面形状近似为三角形,针对顶点C高于液面或低于液面的情况,计算浸入液体中的面积和形心。当顶点C高于液面时,即φe≤φ≤φc,浸入液体中的面积Sim1为
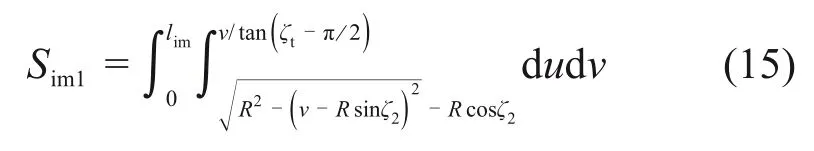
形心在局部坐标系A-uv中的坐标(uP1,vP1)可通过下式计算:

式中:MV1和MU1为浸入液体中辅助鳍平面形状的一阶矩:

当顶点C低于液面时,即φc<φ≤π/2,记LC=R(cosζ1-cosζ2)tan(ζt-π/2),浸入液体中的辅助鳍面积为

形心的坐标(uP2,vP2)为:

式中:MV2和MU2为浸入液体中辅助鳍平面形状的一阶矩:

忽略不同深度压强不同引起的压力分布微小差异,假设液体作用在辅助鳍上的力在浸入液体中的部分均匀分布,则辅助鳍的压力中心P与浸入液体中的部分的形心重合。基于形心的计算公式,可以得到压力中心P到中心轴之间的距离lPY的表达式:

2.4 数值分析结果与讨论
水陆两栖球形机器人的参数为R=175 mm,ζ1=13.7°,ζ2=55.2°,ζt=115°,h=116.4 mm,代入式(11)~(13)计算可得关键角度φe=24.1°,φc=31.9°;φd=155.9°。取CLmax=0.92;CDmax=1.12,进行数值仿真分析。
浸入水中的辅助鳍面积S和lPY随倾角φ的变化曲线如图6所示。由图6可见:面积变化曲线和lPY变化曲线关于φ=π/2 对称。在辅助鳍刚浸入液面和即将离开液体的阶段,S和lPY随倾角φ变化较为显著;而在辅助鳍接近与液面垂直的阶段,面积和lPY随倾角φ变化比较平缓。

图6 面积S和lPY变化曲线Fig.6 Changing curves of area S and length lPY
球形机器人运动稳定后,即球壳以额定转速ωs=2π rad/s 旋转,机器人以额定平移速度|Vs|=0.4 m/s做直线运动时,来流速度幅值|Vw|和攻角αe随倾角φ变化的曲线如图7所示。由图7可知:倾角φ从φe增大到π/2 的过程中,来流速度幅值|Vw|快速减小,攻角先减小再逐渐增大;|Vw|的曲线关于φ=π/2 对称,攻角的曲线关于点(π/2,π/2)中心对称,该点同时是攻角曲线的拐点;|Vw|持续减小的主要影响因素为Vs和-Vn之间的夹角β减小。
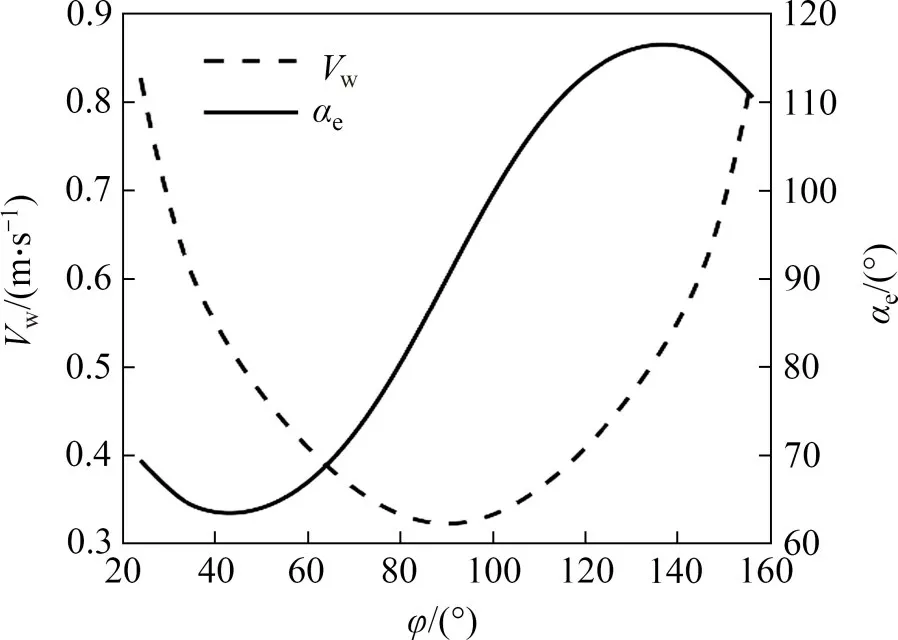
图7 来流速度幅值和攻角变化曲线Fig.7 Changing curves of amplitude of inlet water and angle of attack
运动稳定后,作用在单片辅助鳍上的升力和阻力变化规律如图8所示。从图8可见:在倾角φ从φe增大到π/2的过程中,由于辅助鳍入水面积增大,阻力先从0增大到最大值,然后,由于来流速度幅值|Vw|下降成为主导,阻力缓慢下降;在φ=π/2 即辅助鳍平面与液面垂直时,阻力取得局部极小值,局部极小值约为阻力最大值的一半,此时,|Vw|也取到极小值;阻力变化曲线关于φ=π/2 对称。当φe≤φ≤π/2 时,升力的变化趋势与阻力一致,但是在φ>π/2 后,升力的符号发生了变化。原因在于,以从X轴正向逆时针转过的角度为升力和阻力的相位,当φ<π/2 时,升力的相位超前阻力的相位,当φ>π/2 后,升力的相位滞后阻力的相位,φ=π/2 时升力为0,是相位变化的临界点。升力符号的改变反映了升力和阻力间相位的变化。

图8 升力和阻力变化曲线Fig.8 Changing curves of lift force and drag force
水平分力和竖直分力随倾角φ变化的规律如图9所示。从图9可见:水平分力和阻力有相似的变化规律,但两者的符号相反,竖直分力和升力有相似的变化规律。根据水平分力计算公式,运动周期中,当倾角φ接近φe或φd时,在水平分力的成分中,升力的水平分量占比较大,阻力的水平分量增大了该阶段水平分力的幅值。在倾角φ增大到π/2 的过程中,升力的水平分量占比减小,阻力的水平分量占比逐渐增大;当倾角φ接近π/2 时,阻力的水平分量在水平分力中起主导作用,该阶段升力趋向于0,升力对水平分力的贡献很小。在运动周期的中间阶段,水平分力整体变化较为平缓,辅助鳍能给机器人提供持续稳定的推进力。参考升力和阻力计算公式可知,增大辅助鳍入水面积和球壳旋转速度可提高中间阶段水平分力的幅值。

图9 水平分力和竖直分力变化曲线Fig.9 Changing curves of horizontal force and vertical force
3 液体作用在辅助鳍上的合力
3.1 水平分力和竖直分力计算公式
水平分力和竖直分力关于倾角φ的函数表达式比较复杂,为利于进一步计算和分析,有必要对其形式进行简化。由于水平分力和竖直分力呈现明显周期性变化规律,可用傅里叶方法进行拟合,得到水平分力和竖直分力的傅里叶级数近似表达。m阶傅里叶级数的方程为

将上述方程中的基写为列向量形式:

相应的系数写为行向量形式

则m阶傅里叶级数可以表示为系数向量与基向量的积:
液体作用在辅助鳍上的水平分力可以用傅里叶级数表示的分段函数来描述:
定义带通滤波函数

则上述水平分力又可以表示为

类似地,竖直分力可以表示为

其中:AFX(m)和AFY(m)分别为水平分力和竖直分力对应的系数向量,基向量BFX(m,φ)和BFY(m,φ)的区别在于各自的频率w不同。
3.2 傅里叶级数表示的合力计算公式
当半球壳上配置的辅助鳍数量为n∈N 时,任意相邻的辅助鳍之间的相位差为2π/n。以辅助鳍1作为参考基准,其倾角为φ时,辅助鳍k的相位为

当φe≤φ≤φd且φe≤φk≤φd,辅助鳍1 和辅助鳍k同时位于液面下方,液体作用在辅助鳍k上的力计入合力。辅助鳍k相应的带通滤波函数为

液体作用于辅助鳍k的水平分力为

当FkX(φ)≠0时,将FkX(φ)的表达式用三角函数和差公式展开,分离出其中的常值系数项,表示为系数向量和基向量的积:

式中:WkX(m,k)为系数矩阵,


对作用在半球壳上浸入液面下的所有辅助鳍上的水平分力求和:

则水平分力的合力可以简化为

类似地,竖直分力的合力可简化为

3.3 数值分析结果与讨论
在给定的机器人参数下,利用傅里叶级数对单片辅助鳍水平分力和竖直分力进行拟合,结果如图10所示。从图10可见:在φe≤φ≤φd范围内,当傅里叶级数的阶数m=6 时,水平分力拟合相应的和方差SSE 为0.000 243 2,相关系数R2为0.999 8;竖直分力拟合相应的SSE为0.004 267,R2为0.999 5,显示拟合曲线与原始曲线具有较高的匹配度。

图10 水平分力和竖直分力拟合曲线Fig.10 Fitting curves of horizontal force and vertical force
将水平分力拟合得到的频率和系数向量代入水平分力合力表达式中,计算辅助鳍数量n分别为4,8,12时的水平分力合力,结果如图11所示。

图11 不同辅助鳍数量对应的水平分力合力Fig.11 Resultant horizontal force of different numbers of fin
从图11可以看出:对不同的辅助鳍数量配置,水平分力合力均呈现周期性变化规律。增加配置的辅助鳍数量可以增大合力的平均幅值,平抑合力的波动,从而减小振幅,同时,合力的振荡频率也会增加。其中,当辅助鳍数量为12 时,水平分力合力平均幅值约为0.72 N,振幅约为平均幅值的3.5%,是较为合适的配置方式。两半球壳上的辅助鳍相互对称配置,故作用在球壳整体的合力等于作用于半球壳的合力的2倍。
4 结论
1)利用辅助鳍改善球形机器人水面运动性能,将传统球形机器人的应用环境从陆地拓展到水面,增强了其环境适应性。
2)基于机翼理论推导了液体作用在辅助鳍上的升力和阻力计算公式,给出了水平分力和竖直分力表达式,并利用傅里叶级数对水平分力和竖直分力进行拟合,给出了傅里叶级数表示的水平分力合力和竖直分力合力计算公式。
3)辅助鳍在入水和出水临界状态之间的中间阶段,液体作用在辅助鳍上的水平分力变化平缓,辅助鳍能给机器人提供持续稳定的推进力;提高球壳的旋转角速度和增大辅助鳍的入水面积都可以增大中间阶段作用在辅助鳍上的水平分力,从而提升机器人的推进力;作用在半球壳上辅助鳍上的水平分力合力呈现周期性变化规律,增加辅助鳍数量,可以增大合力的平均值,减小振幅。

