三“效”让女生笑对立体几何

南京航空航天大学苏州附属中学 焦艳琴

曾经听到一个学习非常认真的女生抱怨：看到什么点、线、面总是断电，真想让这立体几何走开！

从整体的角度上讲，男生和女生的思维方式和行为习惯是有一定差别的。男生从小在泥地里面恣意地摸爬滚打，在窗台上上蹿下跳的时候，女孩子只能小心地停留在自己的平面世界里，远远地看着男孩子在属于他们的空间世界里自由地嬉戏。长期的行为方式和社会的角色定位，使男生的视角是立体的，初学就对立体几何很有感觉，而女生的视角是平面的，看到立体图形就经常断电。

事实上，只要抓住女生的特点，扬长避短，完全可以让女生和立体几何握手言和，甚至最终比男生学得还好。我的点滴体会如下：

一、视觉效应

1.练就一双“立体”的眼睛

正是因为很多女生没有“立体”观念，才导致她们的立体几何学习一团糟，根本听不懂教师课堂上在说什么。所以在立体几何的起始课中，我从不讲柱、锥、台，不讲点、线、面，不讲定理、公理与推论，只出示许多图形让她们看，让她们感受。

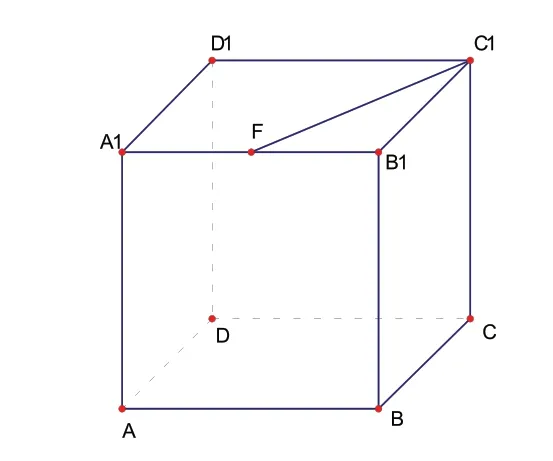
图1

例如：已知正方体ABCD-A1B1C1D1，如图1所示，F为A1B1的中点，那么C1F与AA1有交点吗？如果有的话，试作出这个交点。

在习惯性的“平面”思维的指导下，她们往往直接把C1F与AA1连接，便认为“找到”了“交点”，此时，教师引导她们搭建相应的正方体模型，她们就会迅速认识到自己的错误，恍然大悟。

经过几番这样的训练，她们就可以走出“平面”的小圈子，拥有“立体”的视野。

2.搭建模型，对比认识

刚开始的时候，为了让她们直观地感受到几何元素在立体图形中的确切位置，可以引导她们搭建模型：用手中的笔当直线，用天花板、书本、桌面当平面；可以用纸折，还可以用小刀把橡皮刻出想象中的图形……

例如，让她们观察图2，搭建相应的模型。

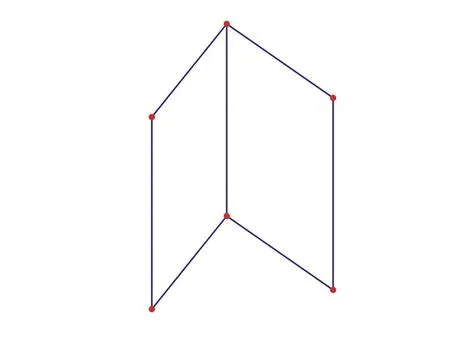
图2

任由她们想象，不同的视角，就能得出不同的结论：竖直放置，书脊在后；倾斜放置，书脊在上。她们展示着、争执着，非常快乐！

二、模板效应

1.建立图形模板

女生的识记方式带有明显的机械识记的成分，习惯“教师讲，自己记，复习背”的学习方式。有些很用心的女生，性质、定理能烂熟于心，但只要点、线、面凑到一起就迷茫、断电。因为缺乏对图形的认知，从而对近在咫尺的条件视而不见，文字结论和图形脱节，怎么可能有“来电”的感觉？那些烂熟于心的定理、定律就真成了纸上谈兵。

因此，在不同的教学阶段，我都从最基本的正方体入手，再缓缓地加以变化，有意识地建立一系列模板，让她们在这些模板中反复感知立体图形，虚实线配合带来“前”“后”“左”“右”的感觉和变化。例如：

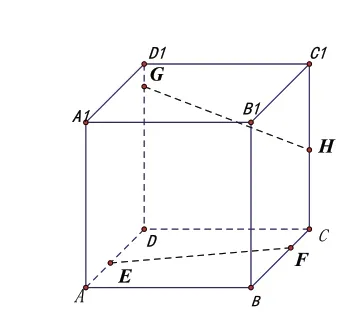
图3

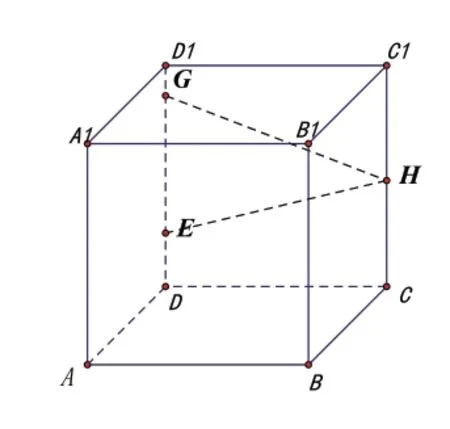
图4

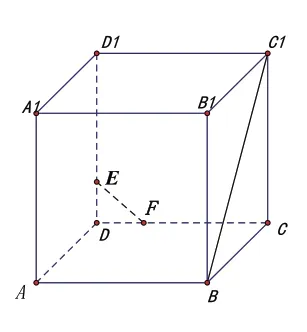
图5

图6

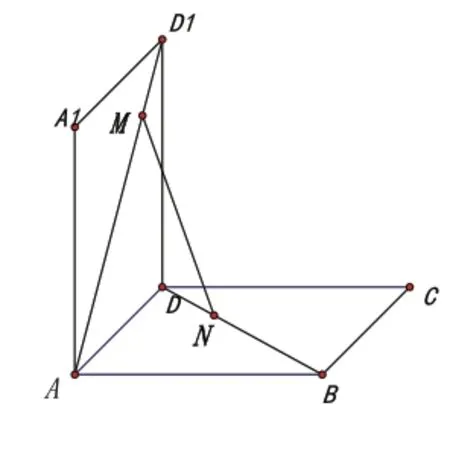
图7

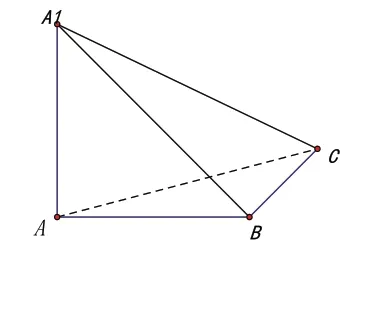
图8

（1）公理2的应用：图3中，若EF、GH相交，试证明EF、GH、DC三线共点；

（2）三点共线：图4中，EH，GH与平面ABCD都相交，证明这两个交点与点D三点共线；

（3）变化：把图4中其他背景撤除，再来证明三点共线；

（4）两条直线的位置关系：在图5中，在所有的面的对角线中找到与BC1异面的直线；

（5）变化：任意两条面对角线所成的角；

（6）再变化：在图5中，EF与BC1所成的角；

（7）线面平行与垂直：在图6中，作出面PBC与面A1B1C1D1的交线；

（8）变化：在面A1B1C1D1中，过点P作直线垂直于直线CP；

（9）再变化：从正方体中抽出图7，DN=D1M，证明线MN与面D1DC平行；

（10）再变化：从正方体中抽出图8，找出此三棱椎中直角三角形的个数；

（11）再变化：在图8中，证明若干面面垂直，找若干面的垂线；

（12）把图形变化为正三棱椎中的一系列问题；

（13）正方体中的三棱柱→正三棱柱→斜三棱柱；

（14）正方体→平行六面体（各面都是夹角为60°的菱形）；……

最后，让这些图形在学生头脑中停留，被她们牢牢记住，逐渐形成自己的空间意识。

2.形成方法模板

建构主义心理学认为，学生用自己的观点解读了教材的内容，从而在头脑中建构出一个新的概念，学习者的学习完全是自主的活动。

当她们真正理解了图形的位置关系之后，引导她们对一些类型问题进行深入研究，得到并形成方法模板，比如证明线面平行的方法：（1）三角形法则（如图9）；（2）平行四边形法则（如图10）；（3）平行平面法（如图11）。

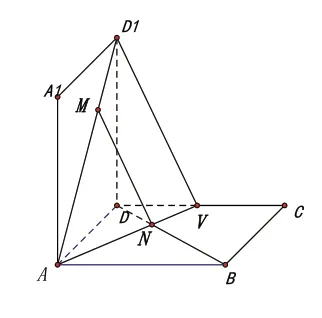
图9

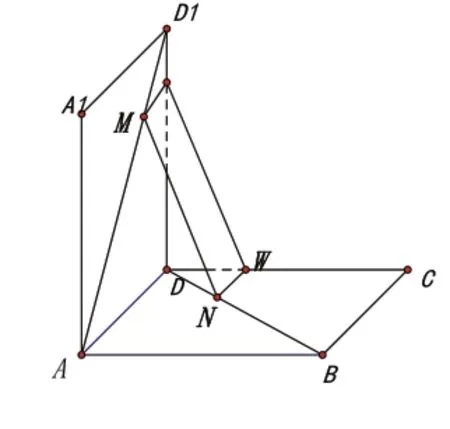
图10

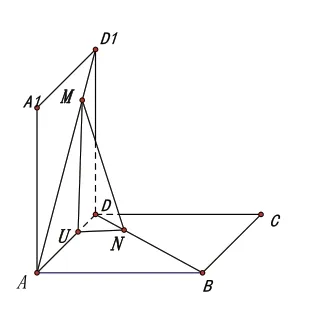
图11

3.探究这些方法的成因

（1）根据线面平行的判定定理，需要在平面中找到与该直线平行的直线；（2）根据线面平行的性质定理，要找的直线必须而且只需与该直线在同一平面内；（3）根据公理3及其推论，两条相交直线确定一个平面（三角形法则的由来），两条平行直线确定一个平面（平行四边形法则的成因）。

引导学生从根源上找到这些方法的成因，才能让她们在头脑中真正建构这些方法模板，并能在实际操作中自如地使用。

立体几何的基本单元是图形，有了图形，点、线、面才有了生命力！只有在图形单元中，她们才能真正地理解使用文字形式与符号形式的性质、定理，才能找到“来电”的感觉。

三、攀比效应

现在的学生都有很强的攀比心理，这种攀比心理简直是无孔不入、无处不在。了解、理解学生的特点，在适当的时间合理利用，可能会得到意想不到的绝佳效果。

1.活跃课堂气氛

美国著名教育家西尔伯曼在其著作《课堂的危机》中提出：课堂的有效性必须体现两个要素：第一，课堂气氛是否走向人性化的理解和相互信赖的班级氛围；第二，学习方式是否转变为使他们更容易接受的方式。攀比心理使学生更愿意说出自己的观点，指出他人的不足之处，且语言生动有趣。

2.有效地形成互动

建构主义心理学还认为，学习是一个互动的过程。攀比心理使学生从内心极不愿意比别人差，所以一旦有人灵光一闪有了一种想法，她们马上就会效仿，同时会急切地寻找其他更优的做法，这样就激活了思维，促使她们的思维向纵深发展，更加强了思维的灵活性，慢慢地，她们将会摆脱原有的模板可能会造成的束缚。

事实上，立体几何是感性和理性的共同体，先有感性的认识，再有理性的推理认证，这其实是与女生的思维路线吻合的：感性地看待事情，理性地处理事情。当她们的眼睛逐渐“立体”起来，已有的套路又能使她们有了成功的体验之后，她们就不再觉得立体几何面目可憎，就有了自信心，有了正视挫折的勇气和战胜困难的决心，再结合教师的科学指导，让她们“举一反三”“触类旁通”，使她们情感与理性并存，既天真可爱烂漫，又严谨细致，她们一定会把立体几何演绎得更加精彩！