小样本下离散广义逆威布尔分布的可靠性统计分析

赵爱红 岳德权

（燕山大学 理学院，河北 秦皇岛 066004）

一、引言

在可靠性试验中为了节约试验时间和经费，即使采用加速寿命试验的方法往往也很难得到完全样本数据，得到的样本数据往往是截尾的。截尾寿命试验分为定时截尾寿命试验和定数截尾寿命试验两种。定时截尾寿命试验指试验到指定时间就立即停止，定数截尾寿命试验是指试验到指定的失效个数停止。II型截尾数据是定数截尾寿命试验下产生的样本数据。在寿命试验中，有时候不能连续测量产品的寿命，或者产品寿命本身就是离散型的数据，比如开关的使用寿命。因此需要对连续型寿命分布进行离散化，得到离散化的寿命分布，以拟合实际的寿命试验数据，并且根据试验数据对产品总体的可靠性进行统计推断。Gusmao F R S和Ortega E MM等[1]提出了广义逆威布尔分布，并且对该分布的一些性质进行了研究。Para B A和Jan T R[2]提出三参数离散广义逆威布尔分布（简称DGIWD），给出了DGIWD完全样本下参数的极大似然估计。

基于截尾数据的可靠性统计推断，学术界有颇多研究。Zaizai Yan和TiefengZhu等[3]研究了基于II型截尾数据针对不同压力试验下威布尔回归模型的点估计和区间估计，以及生存函数参数估计和平均失效时间等可靠性相关的统计推断。彭秀云[4]在广义逐次截尾数据的基础上给出了逆威布尔分布基于贝叶斯统计方法的可靠性推断，并推广到其他的威布尔分布，提出了一个新的修正的威布尔分布。Zheng Zhang和Wenhao Gui等[5]基于II型逐次截尾数据，对广义瑞利（GR）分布进行了统计推断，得到了参数的最大似然估计，构造了参数和可靠度的置信区间；基于平方误差损失函数，提出可靠性函数的贝叶斯估计，得到了点估计和最大后验密度的置信区间估计。在小样本方面，Yi Cui和YongboZhang等[6]提出了一种新的以区间统计为基础的可靠性分析手段，解决了小样本情况下数据缺少的问题，提高了估计的精确度。刘金萍[7]基于Bayes理论对小子样的寿命分布进行可靠性统计分析，提供了一种新的混合威布尔分布的解析方法，在无失效数据情况下给出产品可靠度估计，改进了电力系统中离散马尔科夫链模型出现在同一时间状态停留时间长的缺点，使其可以快速分析电力系统的可靠性。Singh SK和Singh U等[8]在II型截尾数据下，针对连续型逆威布尔分布，给出了参数的贝叶斯估计，并且通过数值模拟对极大似然估计和贝叶斯估计的结果进行了比较。Sultana T和AslamM等[9]针对三变量混合逆威布尔分布的参数进行了贝叶斯估计，并且分别讨论了先验分布采用有信息先验和无信息先验两种情况下的贝叶斯估计。

综上，本文基于II型截尾数据，在小样本情况下运用贝叶斯估计的方法对DGIWD的可靠性进行统计推断，首先给出DGIWD三参数未知情况下参数、可靠度以及失效率的极大似然估计。其次讨论先验分布选取经验分布情况下参数、可靠度以及失效率的贝叶斯估计，并且给出相应的最大后验概率密度区间。最后通过数值模拟进行贝叶斯估计的模拟求解，并且对极大似然估计和贝叶斯估计进行比较。

二、极大似然估计

三、贝叶斯估计

接下来将讨论在小样本情况下更适用的DGIWD的贝叶斯估计。针对先验分布采用经验分布的情况，首先给出DGIWD的三个参数、可靠度和失效率的贝叶斯估计。其次给出贝叶斯区间估计。最后，通过数值模拟对DGIWD的贝叶斯估计和极大似然估计进行比较。

（一）贝叶斯估计原理

贝叶斯学派认为，任何一个未知参数都可以看作是一个随机变量，可以用一个概率分布去描述这个随机变量，而这个分布被称为先验分布。在经典统计学中，随机变量X依赖于参数θ的分布函数记为p（x；θ）；在贝叶斯统计中应当被记为 p（x|θ），被称为 X的条件密度函数。

设从某总体X中抽取n个独立同分布样本，样本的观测值记为x1，x2，…，xn。则此时的样本联合条件密度函数为：

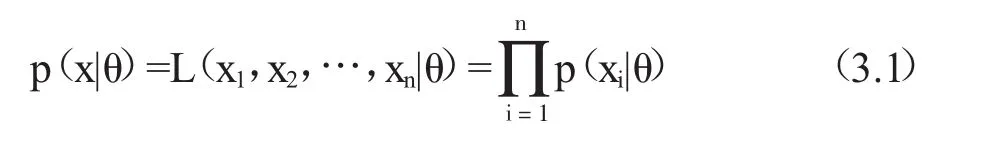
设未知参数θ的先验分布为π（θ），由文献[12]可知θ的后验分布可以写为：

其中符号“∝”表示式（3.2）两边只差一个与θ无关的常数。

在得到参数θ的后验分布之后，进一步要从其后验分布中提取信息，常用的准则是后验均方误差原则，即选择使后验均方误差达到最小的统计量。在均方误差准则下，参数θ的贝叶斯估计就是参数的后验期望 E（θ|x）[13]，即：

并且此时的最小后验均方误差正是后验方差Var（θ|x）。类似地可知，未知参数的函数g（θ）在均方误差准则下的贝叶斯估计为：

（二）三参数均未知情况下的贝叶斯点估计

显然，上述式（3.13）至式（3.17）无法给出显式解。所以，本文要利用蒙特卡洛马尔科夫链（MCMC）方法进行数值求解。在对各参数进行MCMC采样时，需要知道各参数的满条件后验分布，上述各参数的满条件后验分布分别为：

（三）三参数均未知情况下的贝叶斯区间估计

贝叶斯区间估计主要有两种，一种是可信区间，一种是最大后验密度（HPD）可信区间。根据文献[13]对可信区间和最大后验密度可信区间的描述可知，在给定可信水平的情况下，通过后验分布获得的可信区间不唯一，所以本文中的区间估计将采取最大后验密度（HPD）可信区间。HPD可信区间的定义如下：

设参数θ的后验密度为π（θ|x），对于给定的概率1-α（0＜α＜1），若在 θ 的直线上存在这样一个子集 C，满足下列两个条件：

（1）P（C|x）=1-α；

（2）对任给 θ1∈C和 θ2∈C，总有 π（θ1|x）≥π（θ2|x）。

则称为C的θ可信水平为1-α的最大后验密度可信集，简称（1-α）HPD可信集。如果C是一个区间，则称C为（1-α）HPD可信区间。

对于上述（1-α）HPD可信区间，在采用MCMC进行模拟时，根据文献[8]可知，可以从MCMC采样得到的被估参数的序列，通过序列可以得到被估参数的（1-α）HPD可信区间。方法如下：

设{θi，i=1，2，…，M}是 MCMC 采样过程中产生的被估参数的样本序列，其中M是采样总量。对MCMC采样产生的样本序列按照从小到大进行排序可得排序后的序列{θ(i)，i=1，2，…，M}。那么参数 θ 的 100（1-ψ）%HPD可信区间为：

其中j*需满足以下条件：

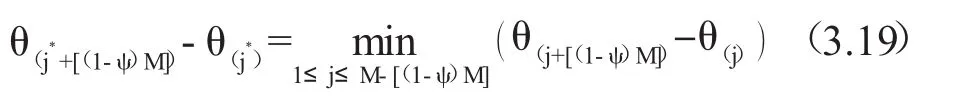
在式（3.18）和式（3.19）中，[x]指不超过 x的最大整数。

四、数值模拟

本节将进行数值模拟求解。本文采用MCMC中的M-H算法，通过不同的抽样方案，给出了三个参数的极大似然估计值和贝叶斯估计值，并且在x=4处给出了可靠度和失效率的极大似然估计值和贝叶斯估计值。进一步，给出相应的置信水平为95%的HPD可信区间。在此，从服从q=0.005，β=1，α=0.8的DGIWD中模拟采样。待估参数先验分布的参数选取a=2，b=2，c=2，d=1.6。已知抽样样本量为n，截尾数量为r，现给出在不同截尾方案下，贝叶斯估计的估计结果如表1和表2所示。在表1和表2中，MLE表示极大似然估计值，MSE1表示极大似然估计的均方误差。Bayes表示贝叶斯估计值，MSE2表示贝叶斯估计的均方误差，HPDI表示HPD可信区间。

表1 不同试验方案下极大似然估计和贝叶斯估计（r=12）

表2 不同试验方案下极大似然估计和贝叶斯估计（r=16）

从表1和表2可以看出，极大似然估计的均方误差和贝叶斯估计的均方误差都非常小，说明在II型截尾数据下，不管采用极大似然估计还是贝叶斯估计，都能获得比较有效的估计结果。因此，在进行产品可靠性统计推断时采用II型截尾数据即能兼顾估计的准确性，又能在寿命试验时节省大量经济成本。

当固定样本量n，增大截尾数量r时，可以看到参数q的极大似然估计值和贝叶斯估计值分别从0.00318211和0.00383738提升到0.00501721和0.00497780，更加接近参数q的真实值0.5。但是，其他未知参数变化很小。因此，增大样本截尾量对估计的准确度虽有一定的提高，但是要考虑提高准确度带来的收益和增大截尾数量导致的经济成本之间的平衡关系。

通过表1和表2可以看到，抽样的样本量为20，属于小样本。虽然截尾方案不同，但各参数的贝叶斯估计的均方误差大部分小于极大似然估计的均方误差。在小样本情况下，贝叶斯估计的准确度显著高于极大似然估计的准确度。并且，贝叶斯估计的HPD区间覆盖了参数的真实值。因此，在小样本情况下，贝叶斯估计要优于极大似然估计。

五、结论

本文研究了小样本情况下，基于II型截尾数据离散广义逆威布尔分布的可靠性统计推断。首先，给出了参数、可靠度和失效率的极大似然估计。其次，在小样本情况下，给出了参数、可靠度和失效率的贝叶斯估计，并且给出了相应的贝叶斯区间估计。最后，数值模拟结果表明，小样本下贝叶斯估计的准确度显著优于极大似然估计的准确度。同时，结果表明选择II型截尾数据是进行产品可靠性推断的一种非常经济有效的选择。