基于无速度参数目标函数的弹着点定位方法

李志明，范锦彪

(中北大学 仪器科学与动态测试教育部重点实验室，山西 太原 030051)

0 引言

弹着点是评价武器着靶精度的重要指标，准确获取弹着点位置对于武器威力评估具有重要意义[1]。弹丸落地爆炸时，会形成破坏区、塑性带以及弹性形变区三个区域，并最终在弹性形变区形成在地下传播的弹性波——地震波。对动能弹而言，当弹丸质量、落地时速度不同时，其对应动能不同，产生地震波的幅值和频率也不同，动能越大，产生地震波的幅值越大，传播的距离也会越远，因此可为弹丸的落点定位提供有用信息。随着微震定位技术发展及在许多领域的应用[2-4]，弹着点定位也得到了越来越多学者的重视。张跃华等[5]改进了Geiger方法和震源扫描算法，并进行联合计算，大幅提高了定位精度并缩短了计算时间；李鹏宇等[6]采用米字形阵列，预先通过来波方向(DOA)算法估计波速，然后将波速估计值代入到达时间差(TDOA)算法中计算初始位置，最后通过泰勒级数算法收敛定位；文献[7-8]通过构建方程组的方式求解弹着点坐标。

目前的弹着点定位方法多数都需要提前测量地震波波速或对其进行反演，但由于地震波在地表介质中传播时在各个方向上的速度都不一致，即便是在同一方向上也会随着距离的增大而衰减，因此会导致定位误差增加。而弹着点定位的关键是得到弹丸落点坐标，无需求解波速，因此本文提出一种基于波速方差的目标函数，并利用单纯形法搜索定位点坐标。然而利用单纯形法进行搜索时，当选择的初始单纯形不同时，定位结果会存在一定的偏差，个别条件下会使目标函数收敛于局部最小值，出现异常的定位结果。本文针对这种情况，采用带噪声的密度聚类(DBSCAN)算法对随机生成不同的初始单纯形进行重复定位的结果进行判别，剔除异常值，对剩余结果求平均作为最终的弹着点坐标。

1 无速度参数测量模型

在定位系统中，可以直接获得的数据只有各个测点的坐标以及测点拾取到的地震波到达时间，弹丸落地的时刻、地震波走时和地震波传播速度等参数难以在第一时间获得，而对于定位来讲，这些恰恰是获得弹着点位置的重要参数，传统采用基于地震波TDOA算法可以有效避免对弹丸落地时刻和地震波走时的求解，但是仍然需要提前测量波速。董陇军等[9]提出基于TDOA的新方法虽然不需要提前测量波速，但是该方法将波速作为未知参数与震源坐标一起反演求解，然而在实际应用中，地震波的传播速度是不均匀的，在地表介质中传播时，各个方向的速度都不一致，即便是在同一方向上也会随着距离的增加而衰减，因此在求解时会导致定位误差增加。李健等[10]提出无需测速的目标函数，虽然不需要提前测量波速以及对波速进行反演，但是，其目标函数较为复杂，当测点数量增加时，运算量也会随之增加。因此，本文提出了如下基于波速方差的目标函数。

假设弹丸撞击地面时，地表发生的是弹性形变，且地面无大型沟渠、无外界干扰源。在待测试区域构建平面直角坐标系，由于坐标系原点所在位置不会对定位结果产生影响，所以可任意指定原点位置。假设弹着点坐标为(x0,y0)，弹丸落地时刻，即弹丸撞击地面的时刻为t0，第i、第j个测点的坐标分别为(xi,yi)、(xj,yj)，第i、第j个测点拾取到的地震波初至时间，即弹丸落地时刻与地震波走时之和分别为ti、tj，地震波传播速度为v，则有

(1)

(2)

两式相减，可得

ti-tj=(Li-Lj)/v，

(3)

式中：

(4)

(5)

易得

(6)

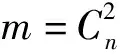
(7)

因此，速度的方差为

(8)

(8)式即为无速度参数的目标函数。

测点的位置坐标是一定的，在一次弹丸落地事件中，测点拾取到地震波的初至时间也是一定的。如果(x0,y0)不是真实的弹着点坐标，那么计算得到的各个速度值之间偏差会较大，因此计算得到的速度方差也会较大。只有真实的弹着点坐标才会使速度方差最小，所以，寻找到可以使速度方差最小的点即为真实的弹着点。

2 模型仿真验证

2.1 模型参数

目标函数(8)式中，未知参数仅为弹着点坐标，无需求解波速，减少了误差来源，具有更高的可靠性。用单纯形法对其寻优即可实现定位，为验证算法是否有效，构建如图1所示的仿真定位模型。假定监测范围为100 m×100 m的区域，共布置8个测点，编号分别为1～8. 在实际应用中，每个测点由一个检波器和一个波形记录仪组成。A、B两点为假定的弹着点。测点及假定弹着点的坐标如表1所示。

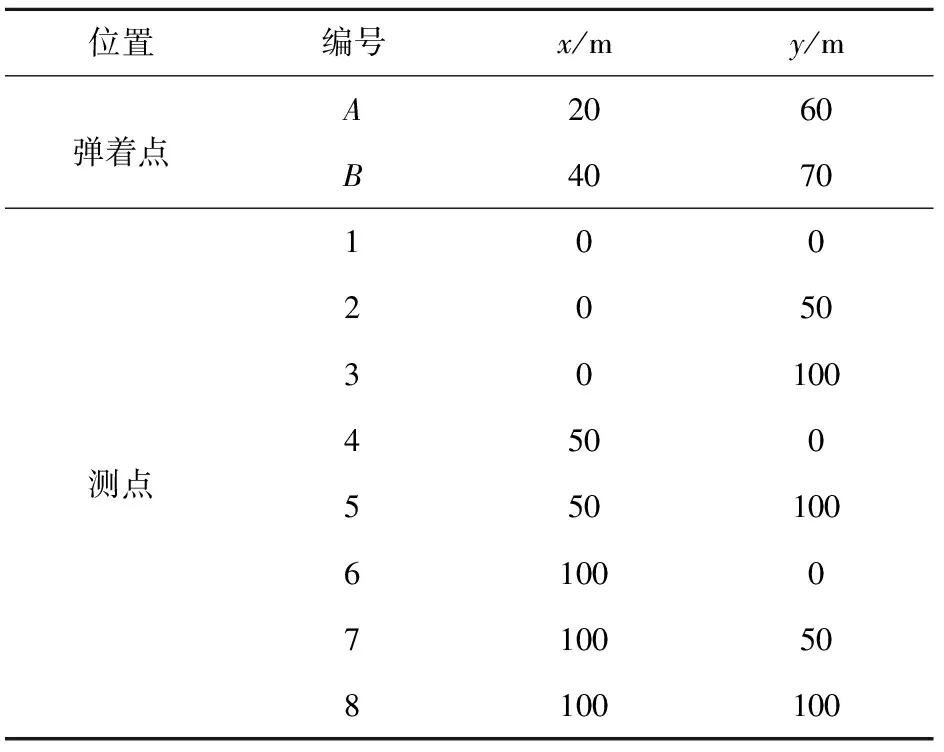
表1 测点及假定弹着点坐标

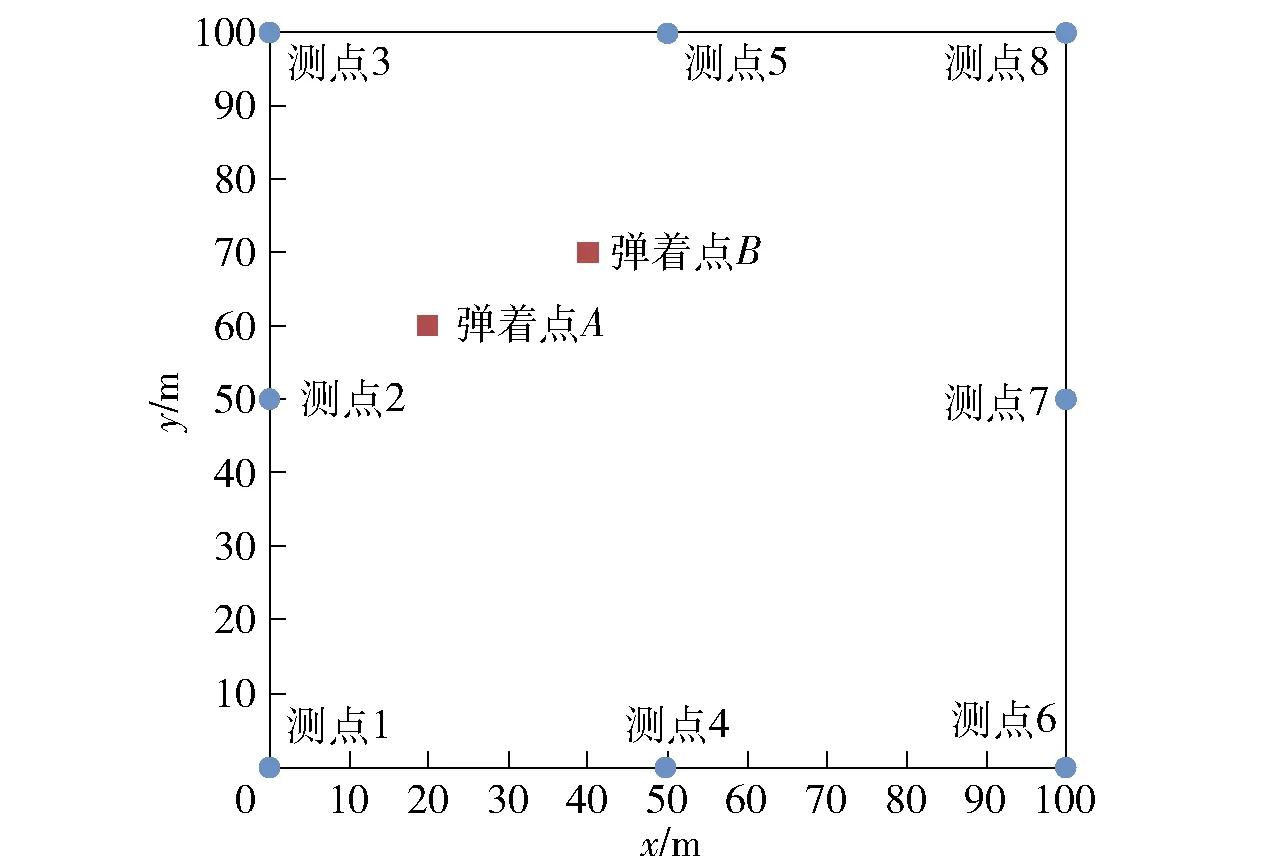
图1 仿真定位模型

假设弹丸落地时刻t0=0 s，地震波的传播速度v0=400 m/s，但由于地震波在地表介质中传播的速度是不均匀的，因此为了尽量模拟实际情况，在弹着点至各个测点的方向上引入±3%的速度误差，引入方式如(9)式所示：

v=400±400×3%×rand，

(9)

式中：rand为0～1之间的随机数。

v代入(1)式即可得到引入速度误差后测点拾取到的地震波初至时间，8个测点拾取到弹着点A和B的地震波初至时间如表2所示。

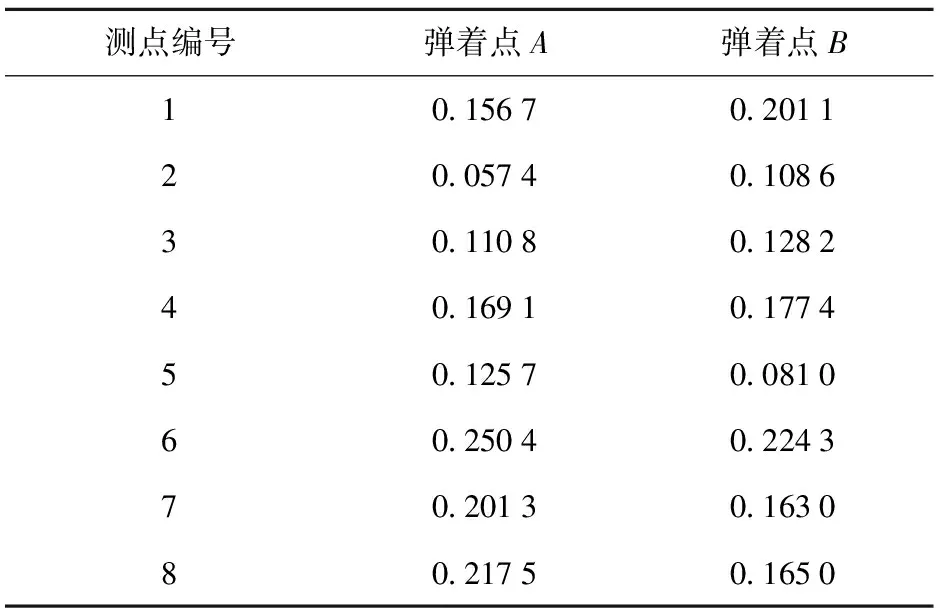
表2 各测点拾取弹着点A和B地震波初至时间

2.2 模型验证

表1所示测点坐标以及表2所示地震波初至时间代入目标函数(8)式，并通过单纯形法搜索其最小值。本文的弹着点定位是平面定位问题，因此单纯形法的初始迭代单纯形为三角形，分别以三角形的各顶点坐标作为弹着点计算3种情况下的目标函数值，根据单纯形法的迭代规则，通过拉伸、收缩、对称等变换，使其不断向着目标函数值最小的方向移动，直到满足迭代终止条件即可得到准确的弹着点坐标，本文中单纯形法的迭代终止条件设为三角形各边长均值不大于5 cm.当选取的初始迭代三角形不同时，单纯形法的定位结果相互之间也会有一定的偏差，甚至会使目标函数收敛于局部最小值，导致出现定位异常的情况。鉴于上述情况，在待监测区域内随机生成不同的初始迭代三角形进行重复定位，观察其定位结果的分布情况。模型中弹着点A和B的200次定位结果分布情况如图2所示。

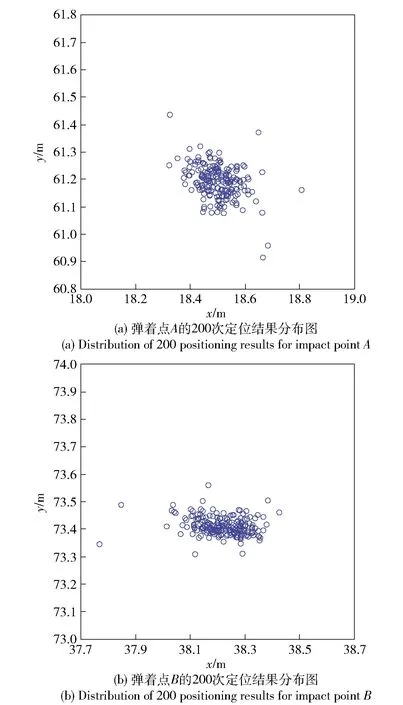
图2 弹着点A和B的200次定位结果分布图

由图2可以看出，200次的定位结果在大多数情况下都比较集中，相互之间的偏差较小，只有少数定位出现异常的情况。

为了最终获得弹着点坐标，需首先剔除定位异常的结果。DBSCAN算法是一维或多维特征空间中的非参数、基于密度的聚类算法。与划分聚类算法不同，DBSCAN算法不需要预先声明聚类的数量，而是通过评估样本的紧密程度来划分对应的类别，理论上可以找出任何形状的聚类。

DBSCAN算法将簇定义为密度相连点的最大集合，可以将数据集中不包含在任何簇中的对象视为噪声，通过这样的方法，能够将定位结果中的异常值剔除。本文中邻域半径ε设置为0.05，密度阈值Minpts设置为4，DBSCAN算法运行结果如图3所示。

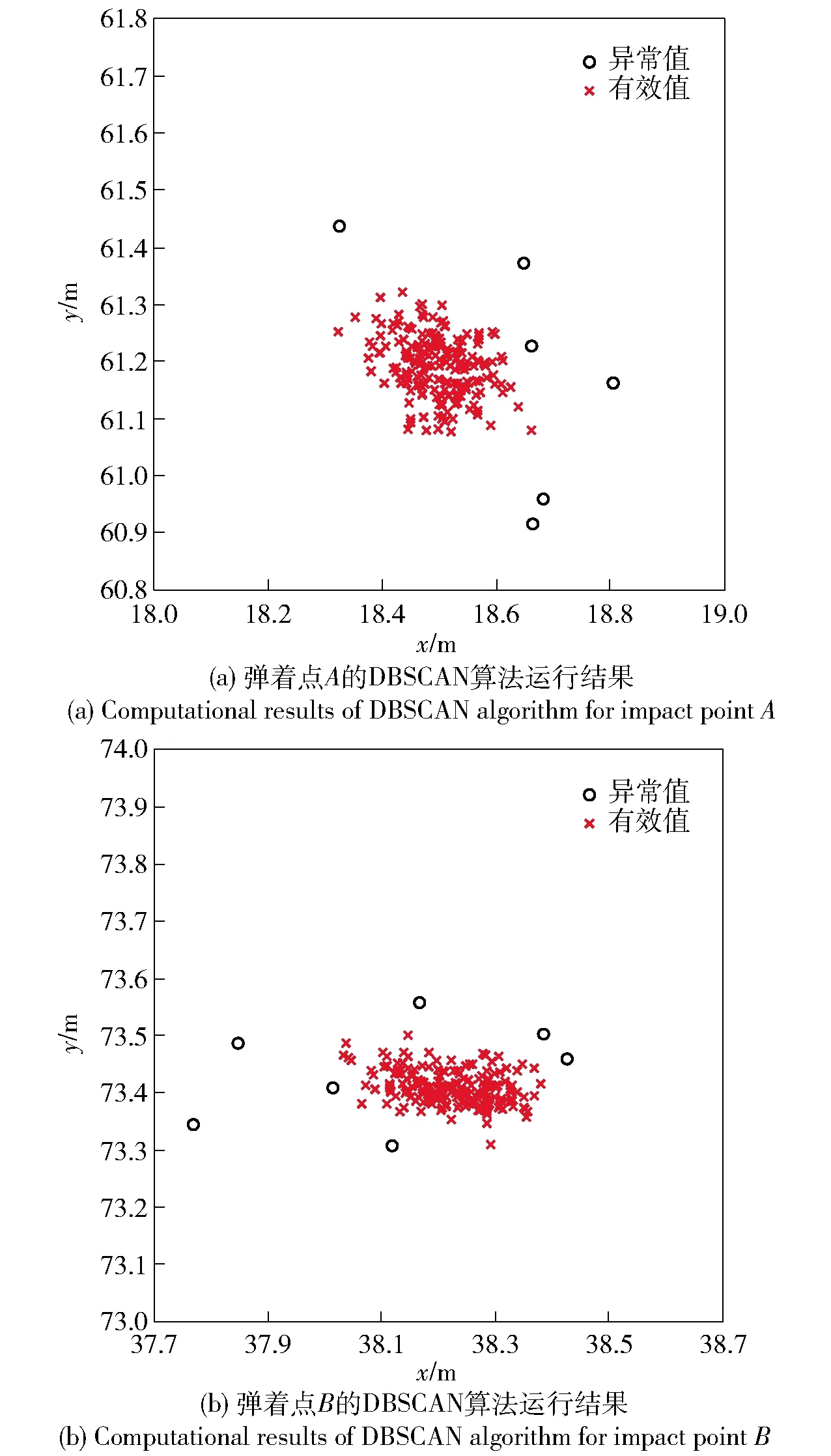
图3 弹着点 A和B的DBSCAN算法运行结果

剔除图3中的异常值后，分别对其余有效值的横、纵坐标分量求均值作为最终的定位结果。弹着点A的最终定位结果为(18.498 6 m, 61.191 6 m)，与A点的距离误差为1.916 8 m；弹着点B的最终定位结果为(38.222 3 m,73.410 3 m)，与B点的距离误差为3.845 9 m.测点至弹着点距离计算误差绝对值平均值[11]为

(10)

式中：n为测点数量；li为计算弹着点位置到各测点的距离；di为实际弹着点位置到各测点的距离。

根据(10)式可得，弹着点A的定位误差为1.97%，弹着点B的定位误差为3.97%，定位误差较小，所以该弹着点定位方法可行。

3 验证试验

本文通过静爆试验对该方法进行验证，静爆试验与弹丸侵彻产生的地震信号一样，都是作用时间短、信号能量高度集中的信号，区别在于静爆是由于超压作用于地面所产生的地震波，而弹丸侵彻是通过撞击产生的地震波。爆炸或者弹丸侵彻地面时都会形成具有一定能量的冲击波，冲击波的压力远远大于土壤的抗压强度，因此靠近震源区域的土壤结构被破坏从而形成破坏区，之后随着能量的消耗，冲击波会衰减为应力波，此时应力波依然会对土壤造成塑性形变，最后随着能量再次衰减，塑性波变为弹性波，即为地震波。

2019年11月在华北某靶场进行了地面静爆试验，药柱当量在50～60 kg梯恩梯(TNT)之间，共布置6个测点，选用西安石油仪器勘探厂生产的动圈式速度型DFJ3A检波器，其主要技术指标[12]如表3所示。

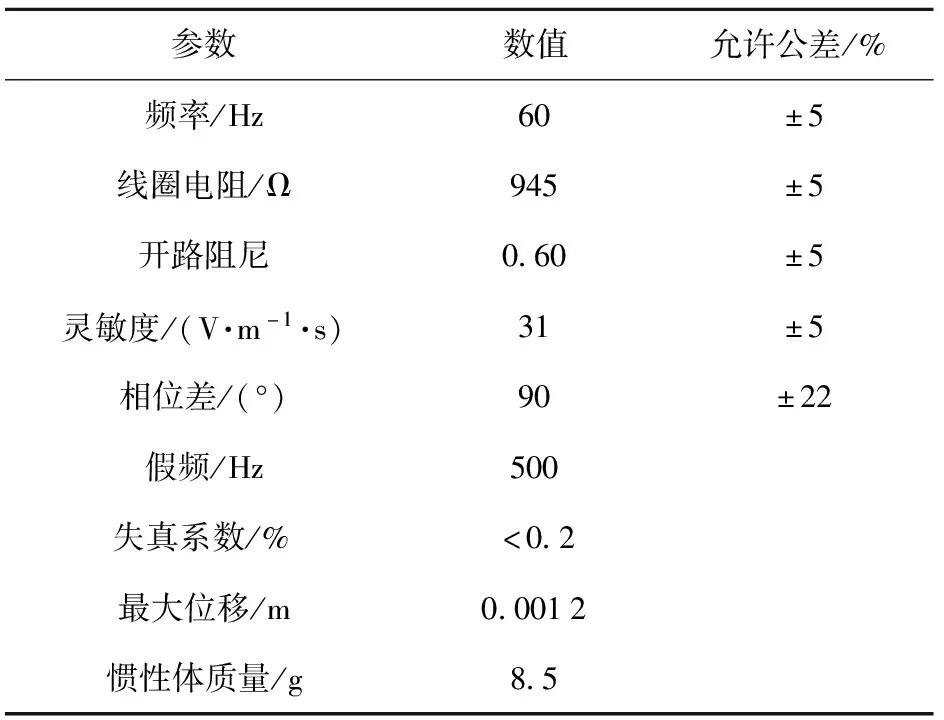
表3 DFJ3A检波器主要技术指标

测点和爆点分布情况如图4所示。图4中，爆点所在位置坐标为(0 m, 0 m)，为保证各个测点保持时钟同步，采用了断线触发的方式，断线的时刻记为0 s时刻，地面静爆试验中所测得的典型地震波信号如图5所示。

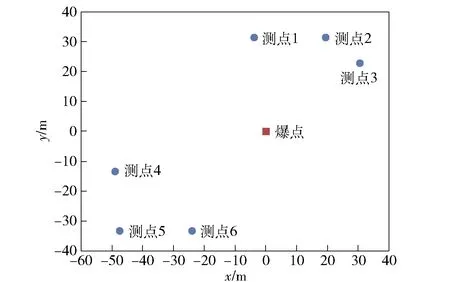
图4 爆点和测点分布图

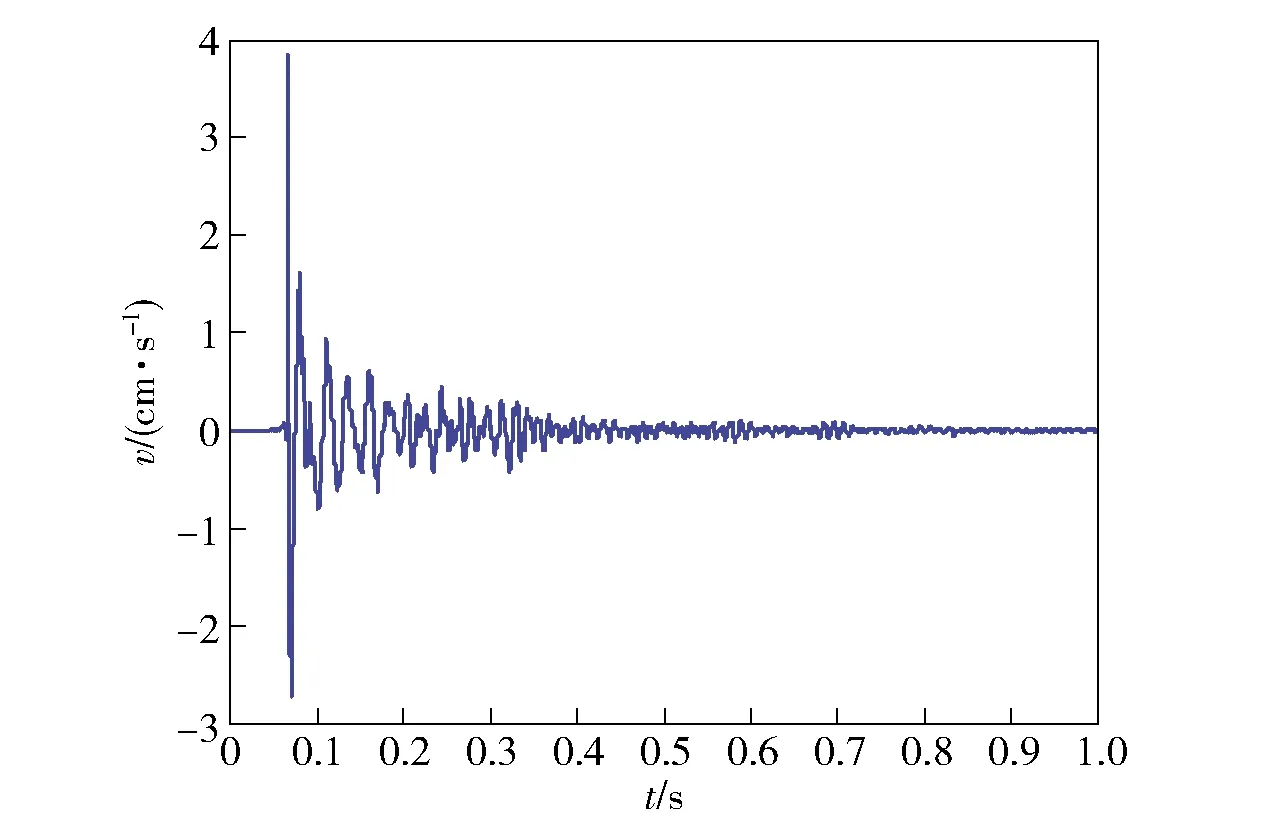
图5 实测典型地震波信号

测点坐标以及各个测点拾取到的地震波初至时间如表4所示。

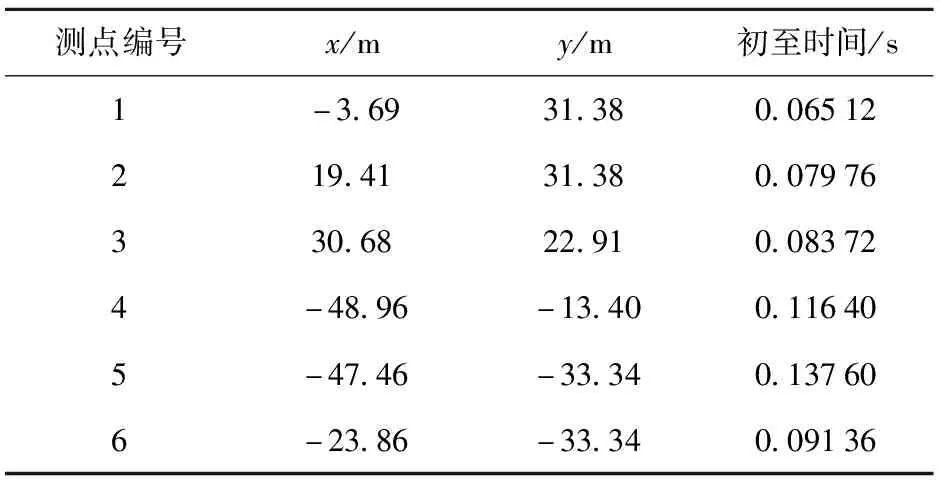
表4 测点坐标及地震波初至时间

同样，表4中数据代入(8)式并通过单纯形法进行200次定位，定位结果的分布情况如图6所示。

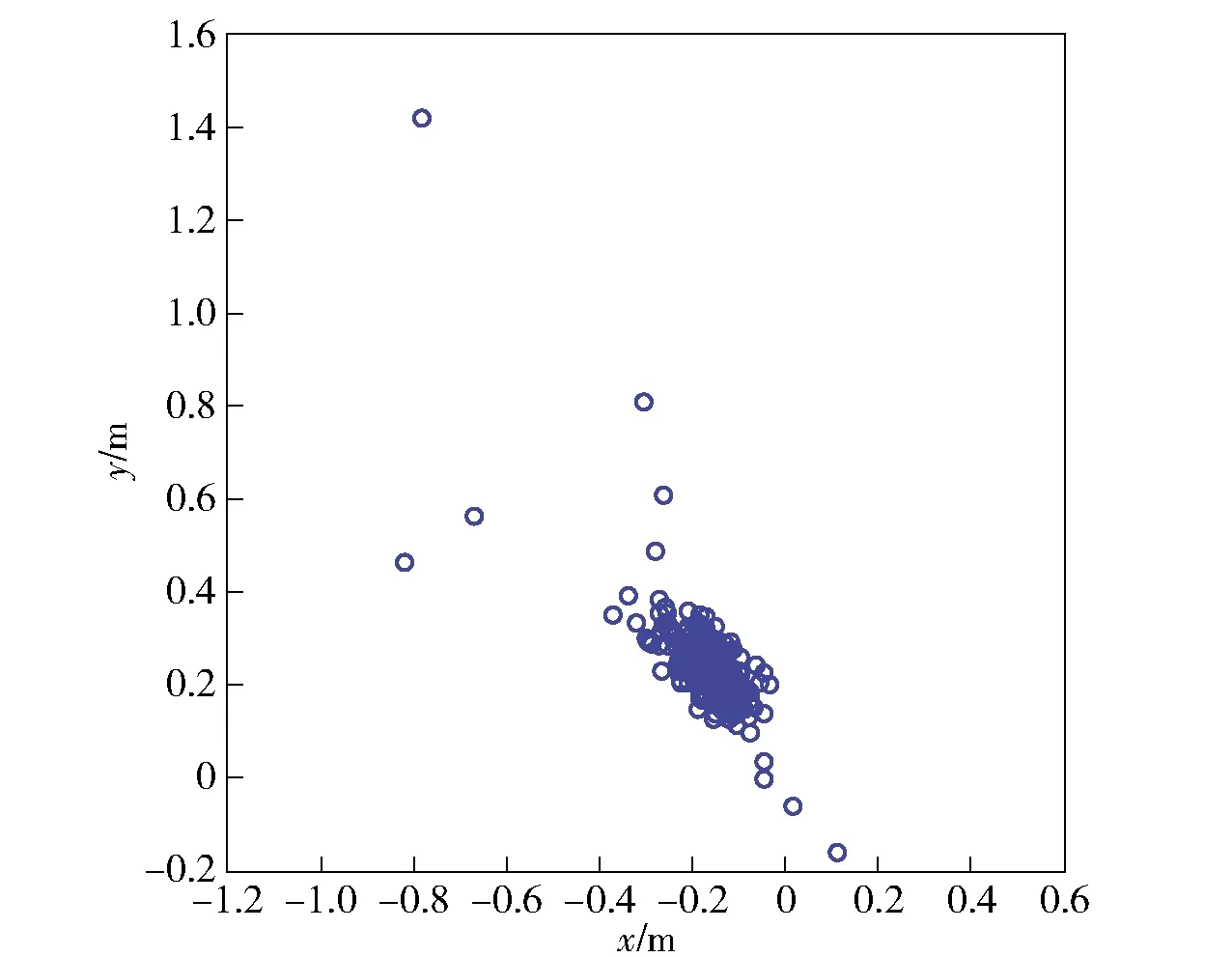
图6 实测200次定位结果分布图

由图6可以看出，与仿真定位模型的结果相似，也出现了少量定位异常的情况，DBSCAN算法的聚类结果如图7所示。剔除图7中异常结果后，分别对其余结果的横、纵坐标分量求均值，即可得到爆点的定位结果为(-0.166 1 m, 0.239 0 m)，与真实爆点位置的距离误差为0.291 1 m，测点至爆点距离误差绝对值的平均值为0.38%.

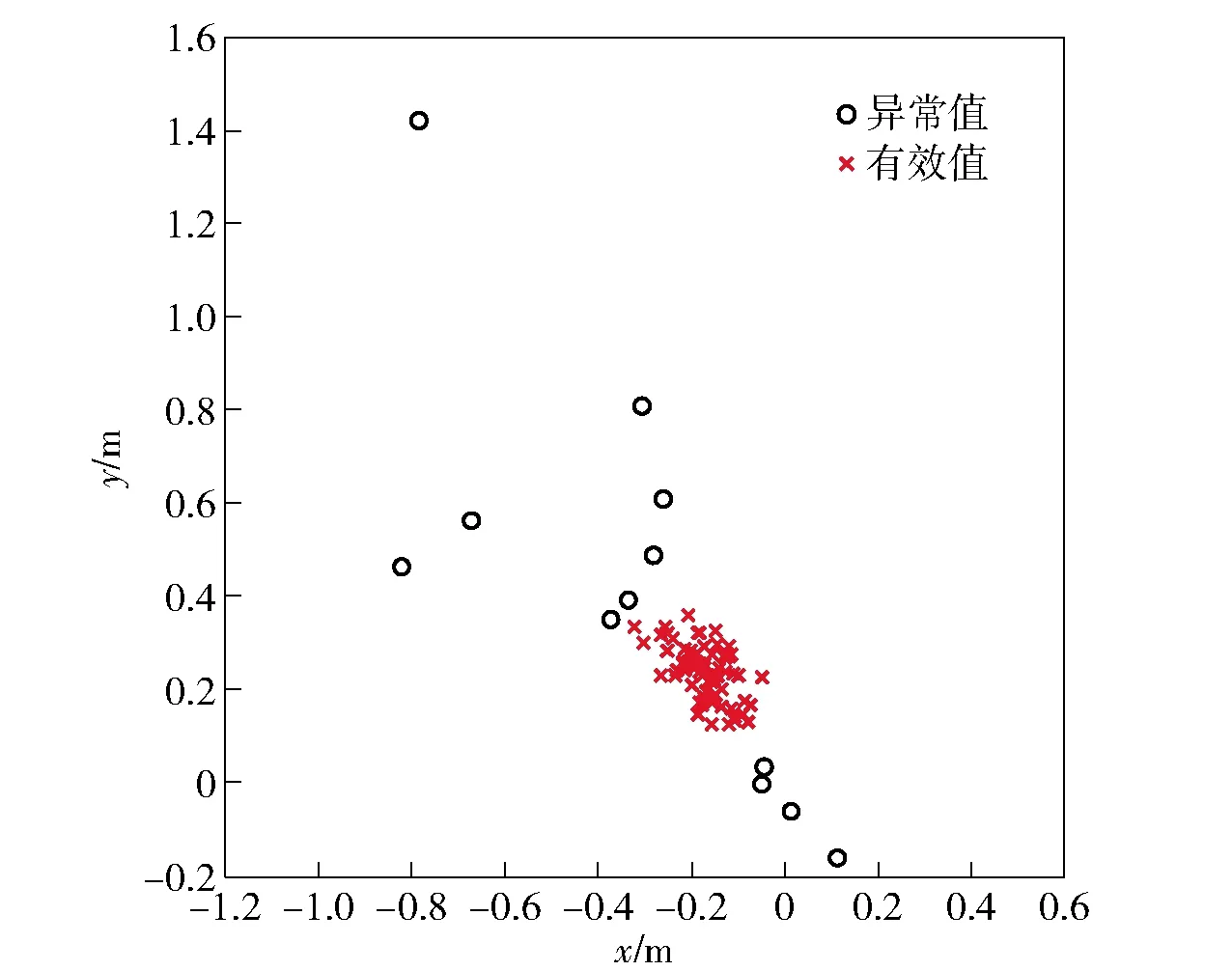
图7 实测DBSCAN算法运行结果

4 结论

本文提出一种基于波速方差目标函数的弹着点定位方法，通过仿真定位模型和地面静爆试验对该方法进行验证。得出以下主要结论：

1)用单纯形法对基于波速方差的目标函数寻优并结合DBSCAN算法可以有效实现弹着点定位。

2)该弹着点定位方法无需提前测量地震波波速或对波速进行反演，可以减小地震波波速不均匀性给定位结果带来的误差，提高定位精度。

然而，静爆与弹丸侵彻产生的地震波存在较大差异，所以不宜采用静爆试验作验证，但在本文的目标函数中已经排除了波速的影响，且没有用到幅度和频率信息。所以仍有一定的借鉴意义，后续将进行大当量战斗部试验进一步验证。