行星滚柱丝杠的设计与有限元分析研究*

晁 瑞 李志峰 梁智鸿 吕瑞虎

(陕西理工大学机械工程学院，陕西 汉中 723000)

行星滚柱丝杠是指丝杠将多个滚动单元的旋转运动转化为直线往复运动，同时依靠滚动摩擦将动力转换为螺母直线运动的精密动力传动装置[1]。该装置属于线接触，通过螺纹啮合来传递力，具有摩擦小、效率高、寿命长等优点。同时，其额定动载比同规格滚珠丝杠副高出3倍以上，被广泛应用到飞机、导弹、卫星等军事领域和石油化工、精密机床、食品包装、医疗器械等民用领域[2-4]。行星滚柱丝杠具有其他传动装置无法比拟的刚度和精度，得到了越来越多的重视[5]。

行星滚柱丝杠的前沿技术目前被国外一些发达国家所垄断，国内研究处于初级阶段。其中，靳谦忠等[6]通过有限元分析对比了行星滚柱丝杠副与滚柱丝杠副的静刚度；Lisowski F[7]对行星滚柱丝杠副的位移分析与载荷分布进行研究，分析了各组成部分之间的载荷盈利分布情况及不同尺寸的螺纹接触刚度；张大伟等[8]提出并探讨了一种适于滚柱零件上螺纹和花键同步滚压塑性成形新方法；董永等[9]对行星滚柱丝杠副滚柱的成形及装配方法进行了研究；而本研究旨在以单螺母行星滚柱丝杠进行理论分析，以工作原理和结构设计方法为前提；以滚动轴承原理为基础，推导了行星滚柱丝杠的承载能力、效率和寿命等相关计算公式；同时计算出了额定动载荷、效率计算与寿命计算[10]，分析其性能，为我国装备制造业的现代化和数控机床的高速化提供参考。

本文取丝杠头数为5，标准直径30 mm，导程10 mm，螺距为2 mm，结构采用单螺母为条件，主要研究内容有：

(1)利用SolidWorks对计算出的行星滚柱丝杠进行数字化建模和虚拟装配，分析各部件之间是否有干涉、配合公差是否符合要求等问题，确定装配无误。

(2)利用Simulation模块对行星滚柱丝杠在同一支撑方式下的轴向载荷进行螺纹啮合部位的静应力、疲劳破坏等分析，得到机构承受极限静载荷时螺纹牙的应力、应变、寿命分布情况。

1 行星滚柱丝杠的结构参数化设计

在设计过程中，为了保证传动比为常数，依据工作原理和几何条件判断，所设计的行星滚柱丝杠主要参数如表1所示。

表1 行星滚柱丝杠的主要参数

2 行星滚柱丝杠数字化建模

2.1 零件参数化建模

(1)丝杠

丝杠采用5头螺纹，牙型角为90°，先在丝杠主体端部进行螺纹的绘制，再绘制螺纹起止线，螺纹起止线要超出螺纹的长度，同时注意截面位置和丝杠中径的关系。其模型如图1所示。

(2)滚柱

在SolidWorks国标设计库里选择相应的齿轮并设置好齿轮参数，导入CREO 3.0，通过输入函数绘制齿轮渐开线，去除材料后得到滚柱端部齿轮；由于丝杠、螺母、滚柱依次相互啮合，因此螺纹旋向和螺距都相同，本文选用三角形螺纹，牙型角为90°，得到滚柱模型如图2所示。

(3)螺母

本文研究的是单螺母行星滚柱丝杠，单螺母与其他零部件进行连接，考虑到零件的实际加工和效率，将螺母和法兰盘单独制造，最后用紧定螺钉装配在一起，这样便于加工。螺母模型如图3所示。螺母完成后需要添加类似法兰的零件，用紧定螺钉连接，其结构如图4所示。

(4)内齿圈

内齿圈的齿和滚柱端的螺纹齿啮合，因此内齿圈的建模方法和滚柱端的螺纹齿类似，具体建模参考滚柱螺纹齿的过程。内齿圈结构如图5所示。

装配时，先把螺母导入装配体，自由度为0；导入内齿圈，约束与螺母共轴、与面接触，并保证内齿圈和螺母的螺纹连续，自由度为0；导入保持架，约束方式是轴线、面的重合，自由度为1；再导入一个滚柱，与保持架上面的孔保持重合，同端面共面，相对保持架的自由度为1；约束完成后调整丝杠和滚柱螺纹的相位角，使之正确啮合，整体没有干涉现象。装配体如图6，整体干涉检查结果如图7所示。

2.2 零件装配

同理，根据滚柱端齿轮和内齿圈的啮合关系，当滚柱上一点自转距离和滚柱公转到下一个位置的距离相等时，根据式(1)可以得出装配第二个滚柱时要设置面与面之间的夹角为229.090 9°，后面需要装配的10个滚柱与上一个滚柱有相同的夹角。

(1)

得：α= 229.090 9°，式中α即为两个滚柱FRONT面的夹角。

3 行星滚柱丝杠模型分析

3.1 有限元分析

行星滚柱丝杠承受轴向力，内齿圈和滚柱端螺纹齿的啮合是周向啮合，且整体对称，为了减少计算量快速准确地得出结果，取丝杠和螺母的1/11和一个滚柱啮合；根据行星滚柱丝杠的特点，保持架在丝杠转动时约束滚柱不发生周向偏移，本文只分析与滚柱相接触部分的螺母和丝杠的运动，所以将保持架和螺母固定在一起分析行星滚柱丝杠的轴向受力情况[10]，采用Simulation进行接触分析。

约束零件的过程与2.2节零件装配过程相同。丝杠、螺母、滚柱的材料均为高碳铬轴承钢(CGr15)，该轴承钢的主要性能参数为弹性模量2.19×105MPa，泊松比0.3，密度7.83×103kg/m3。

把丝杠所受的轴向力等效加载至滚柱上，丝杠和螺母固定，这样就可以减少迭代计算量且计算结果几乎不受影响。同时，丝杠和螺母之间有相互作作用力，作用力设定为3 000 N，在滚柱端部添加垂直于滚柱端面的等效载荷，并确定力的方向。零件固定方式如图8所示。

零件固定约束设置结束后，需进行划分网格。网格划分的质量直接决定计算量和计算结果的精度。由于丝杠、滚柱、螺母均有螺纹且主要分析螺纹啮合强度，为了提高精度，以基于曲率的网格为依据，输入具体参数，随后运行网格化命令。网格划分结果如图9所示。

3.2 结果和数据分析

(1)静应力分析

通过对模型添加材料特性、运动约束、零件接触类型设置等操作后，运行特定的算例，即可得到运算结果。网格信息显示节点总数14 904个，单元总数61 984；网格类型为实体网格，单元大小为1.470 06 mm，公差0.073 502 8 mm，网格品质良好。模型信息的汇总如表2，模型载荷信息如表3所示。

表2 模型信息

表3 模型载荷

通过上述步骤，分析计算得丝杠和滚柱啮合部位应力分布见图10～11；螺母和滚柱啮合部位应力分布见图12～13；应力较大处的细节见图14～15。

由Von Mises云图可知，滚柱螺纹齿与丝杠螺纹啮合部同时受到轴向力，滚柱螺纹齿不完整，易造成应力集中；滚柱与丝杠螺纹啮合时受到轴向力，即啮合部位由螺纹中径部分向螺纹大径方向发生偏移，因此造成螺纹顶部应力过大。

(2)模型位移分析

由于滚柱装配前留有间隙，受力后滚柱发生轴向运动，直到滚柱与丝杠、螺母接触后在载荷的作用下发生位移，对丝杠和螺母的位移分析结果如图16～17所示。

由图16，图17可知，应力主要集中在螺纹大径顶部，而应变主要集中在螺纹小径底部方向。螺纹截面是三角形，当上部受力时下部的变形就会比上部大，丝杠最大变形约为0.005 mm，螺母最大变形为0.002 mm。

(3)模型应变与接触分析

根据胡克定律，在一定的比例范围内应力与应变成线性比例关系，受到应力的部分相应的也会发生应变，此处的应变不同于位移[11]。滚柱、丝杠及螺母在应力接触部位发生的应变如图18～20所示。

见图21～23，半透明部分是当受到轴向载荷时没有有效承载载荷的部分，深色部分是与其他部件接触时主要承载载荷的部分。以此为依据，在以后设计中可以增加有效承载载荷的部分，适当减小图中半透明部分没有承载载荷的部分。

3.3 整体模态分析

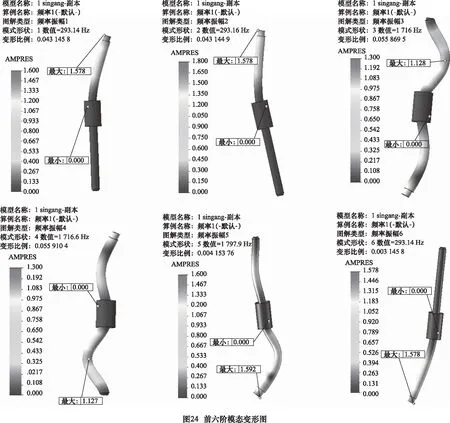
模态分析时丝杠一端固定，螺母位于丝杠中央，螺母固定，固定面选择丝杠一端支撑和螺母表面。整体模态分析网格划分时网格品质高，最大单元大小为3 mm，最小单元为0.6 mm；节点总数303 770个，单元总数为203 759个。模型网格划分完成后选择FFEPlus解算器运行分析，得到前六阶模态变形图，结果如图24所示。

由图24可以发现危险频率在293 Hz、1 716 Hz、1 797 Hz附近；由表4可知，振幅X、Y、Z方向最大的位移分别为0.493 2 mm、3.136 1×10-8mm、0.496 97 mm。

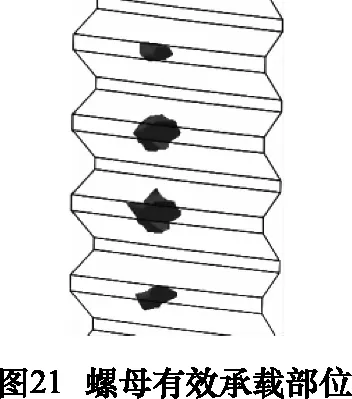
表4 质量参与(正方向的最大振幅)

3.4 疲劳分析

通过静应力分析得到模型的具体数据，模型载荷中循环数设置为 1 000 000次，比例因子为1，步长取1，通过模型寿命和载荷因子等测试进行疲劳分析。

(1)模型寿命

寿命测试是在静应力分析的基础上，使静载荷变为交变载荷，持续加载在模型上，累计每次加载的结果，由图25～26可知，滚柱螺纹齿寿命最短，大约只能承受100次交变载荷就会失稳；滚柱螺纹寿命大约是6 499次，螺母和丝杠的螺纹除了局部区域寿命在100 000次左右，其余的部分寿命大都在900 000次以上。疲劳破坏可能部位如图27～28所示。

(2)载荷因子

载荷因子是反映零部件承受载荷大小的能力，载荷因子越大说明承载能力越强，越不容易发生变形和疲劳等破坏[12]。载荷因子如图29～30所示。

通过分析发现滚柱螺纹齿和丝杠啮合的部位易发生应力集中和疲劳破坏，滚柱螺纹和内齿圈在轴向载荷下几乎不会对滚柱端部的螺纹齿产生影响，因此根据分析结果，将啮合时原先滚柱螺纹齿部位变成齿轮，与丝杠螺纹不啮合，这样就避免了滚柱螺纹应力过大而过早发生疲劳破坏。

4 结语

本文建立了行星滚柱丝杠的几何模型，结合有限元分析方法对模型进行了稳态静力、疲劳寿命和模态分析，明确了行星滚柱丝杠工作过程中各部位的变形及应力分布状况。归纳如下：

(1)建立了行星滚柱丝杠的整体模型，螺纹和齿部分进行了精确的参数化建模，为后面的分析提供了准确的模型。

(2)研究了1/11行星滚柱丝杠的变形，不仅考虑到载荷对模型整体的影响，还定义了模型接触面之间的摩擦系数，更接近实际情况。

(3)分析了行星滚柱丝杠在轴向载荷作用下螺纹的接触应力和疲劳寿命，以及在一种固定方式下的模态分析，分析其振幅对螺纹的变化和对整体传动精度的影响。